2. 河北省矿业开发与安全技术重点实验室(华北理工大学),河北 唐山 063000
2. Hebei Provincial Key Lab. of Mine Development and Safety Technol. (North China Univ. of Sci. and Technol.), Tangshan 063000, China
渗透破坏是影响尾矿坝稳定性的重要因素之一。中国尾矿坝主要以上游式为主,由于尾矿粒径与排放方式的差异,造成尾矿坝不同位置处细粒含量的不同,这势必会导致尾矿砂渗透特性的变化,进而对尾矿坝稳定性造成不同程度的影响,故开展不同细粒含量尾矿砂的渗透特性研究,这对尾矿坝稳定性分析具有重要意义。
目前,相关学者已经对砂土细粒含量对其性质的影响进行了广泛的研究,普遍认为砂土细粒含量变化引起的孔隙比变化是其性质发生改变的重要原因[1-4]。Naser[5]对黏粒含量变化情况下砂土的强度参数与土水特性进行了分析,认为当黏粒含量超过40%时以上两种性质不再发生变化。刘雪珠等[6]对黏粒含量变化情况下的砂土进行动力性能试验研究,得到了砂土动强度与黏粒含量之间的关系。曾长女[7]通过全自动多功能静动三轴试验,对细粒含量变化情况下的粉土液化过程进行了研究。Phan等[8]通过对0~60%粉粒含量的粉砂开展固结不排水三轴试验,确定了粉砂的临界粉粒含量为50%。张超等[9]通过对不同细粒含量情况下的尾矿材料进行研究发现,细粒含量为35%时铜矿类尾矿材料的抗液化性能最好。许增光等[10]对化学淤堵作用下的尾矿砂渗透系数变化规律进行了研究。张媛等[11]对酸碱溶液影响下的含硫尾矿砂渗透特性进行了研究。曾晟等[12]对结构特征影响下的尾矿砂渗透性进行了数值模拟研究。弭玉娟[13]对围压、干密度和孔隙比影响下的尾矿砂渗透系数变化规律进行了分析。目前,针对细粒含量变化情况下砂土性质的研究,主要集中于强度参数与抗液化性能,对细粒含量变化情况下,渗透特性的研究较少。同时,针对尾矿砂渗透性的研究主要集中在结构特征、围压、干密度和孔隙比等因素影响下的渗透系数变化规律,既没有体现细粒含量变化对渗透系数的影响,也没有提出针对尾矿砂的渗透系数计算方法。
铁尾矿砂作为一种特殊土体,其渗透特性尚不明确,应用现有针对其他土体的渗透系数计算公式对其渗透系数进行计算,结果不一定准确。同时,由于铁尾矿砂本身特性,其细粒含量不尽相同,势必引起其渗透特性的变化。因此,有必要对现有针对其他土体的渗透系数计算公式准确性进行验证,并建立适用于铁尾矿砂的渗透系数计算模型。本文通过现场取样,从细粒含量FC(0.075 mm以下细粒含量)、级配、粒径、比表面积和粉粒间孔隙比等多个角度出发,对铁尾矿砂原状样的渗透性质进行了分析,并提出了适用于铁尾矿砂的渗透系数计算公式。
1 砂类土颗粒接触状态Thevanayagam等[14-15]发现:细粒含量FC不同,砂类土的接触状态也不尽相同。当FC比较小时,粗粒砂之间直接接触,构成了沙土的骨架,细粒填充于粗粒构成的孔隙之间。此时,可以用粒间孔隙比
| ${e_{\rm{s}}} = \frac{{e + FC}}{{e - FC}}$ | (1) |
| ${e_{\rm{f}}} = \frac{e}{{FC}}$ | (2) |
细粒含量FC值变化引起砂土性质变化时,必然存在一个临界值,Rahman等[16]提出了
| $F{C_{{\rm{th}}}} = 0.40 \times \left(\frac{1}{{1 + \exp (\alpha - \beta \chi )}} + \frac{1}{\chi }\right)$ | (3) |
式中:
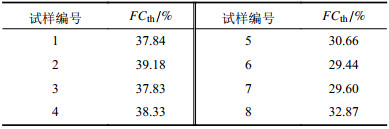
结合铁尾矿砂试样,对铁尾矿砂的
| 表1 FCth值计算结果 Tab. 1 Calculation results of FCth |
 |
2 渗透试验 2.1 试验材料
试验所用试样取自福建马坑矿业股份有限公司的陈坑尾矿库。取样前,将内壁抹好凡士林的环刀装入取样器内。取样时,在尾矿库内,埋深相同,但距子坝距离不同处,用取样器取原状铁尾矿砂试样,一次取样完成后,迅速将取样器和试样密封,更换取样器后,循环操作,共取得原状铁尾矿砂试样8组,其级配曲线如图1所示。所选试样干密度均在2.10 g/cm3左右。
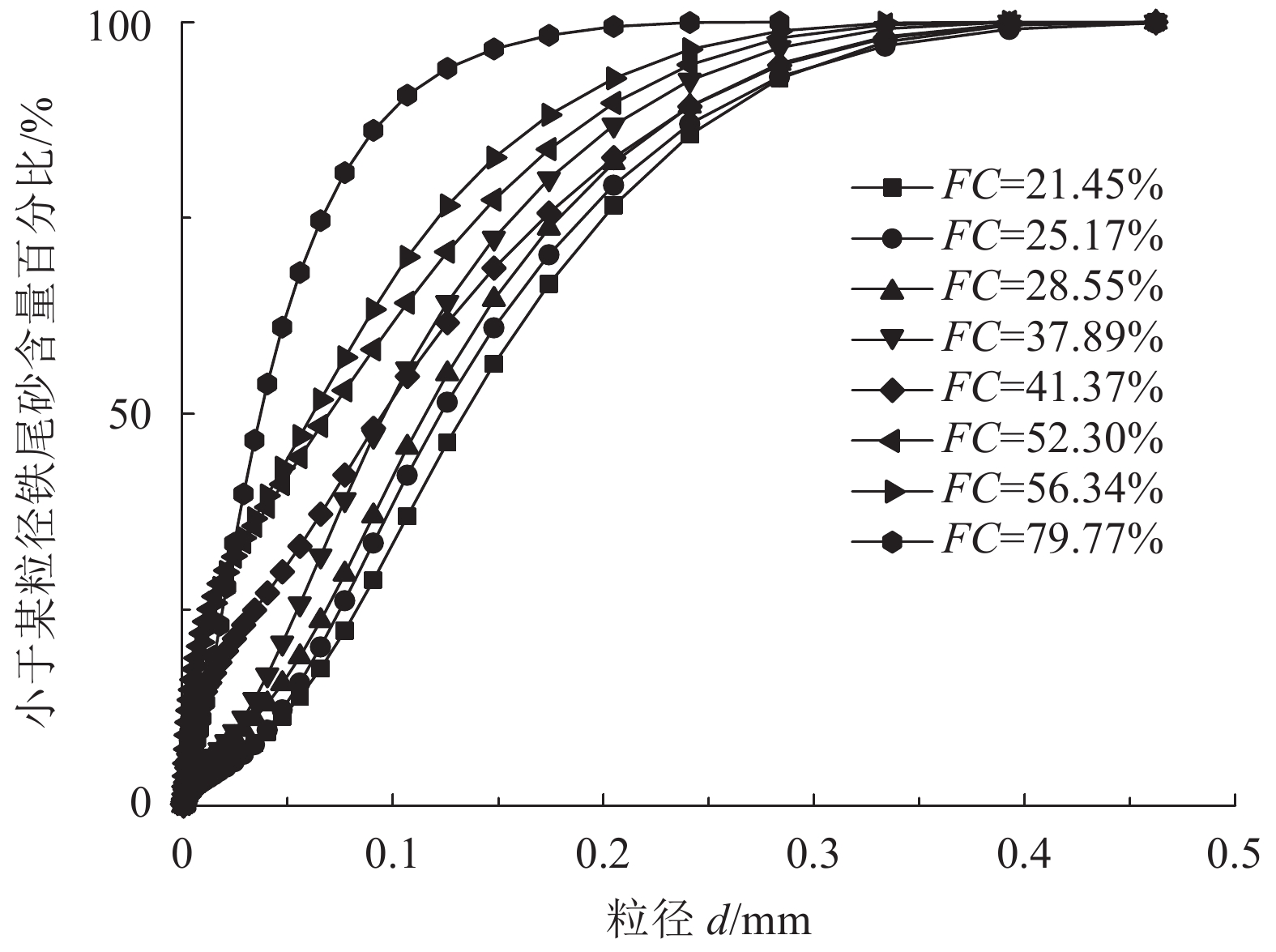 |
| 图1 不同细粒含量铁尾矿砂级配曲线 Fig. 1 Gradation curves of iron tailings sand with different fines content |
2.2 试验仪器与试验方法
试验选用55型渗透仪,将在尾矿库内取得的原状样放入渗透仪内,直接进行变水头试验,仪器内环刀直径61.8 mm、高40 mm。将试样进行饱和后,排尽渗透仪内部空气。设定初始水头,记录水头高度变化时对应的时间,并记录试验水温,如此重复操作6次。最后按照《土工试验规程》(SL 237—1999)中的计算公式,对原状铁尾矿砂的渗透系数进行计算,去掉相差较大的数据后,取平均值。渗透系数K计算公式如下:
| $K = 2.3\frac{{{\eta _T}aL}}{{{\eta _{20}}A({t_2} - {t_1})}}\lg \frac{{{H_1}}}{{{H_2}}}$ | (4) |
式中:a为变水头管断面积,cm2;L为渗径,即试样高度,cm;t1和t2分别为测读水头的起始和终止时间,s;H1和H2分别为起始和终止水头;
不同细粒含量下原状铁尾矿砂的渗透系数如图2所示。从图2中可以看出:随着FC值的增加,渗透系数逐渐减小,曲线可以分为两个阶段。当FC小于40%左右时,渗透系数急剧减小;当FC大于40%左右时,渗透系数基本不再发生较大变化,呈现缓慢减小的趋势。Nagaraj等[17]认为,当细粒含量FC超过40%时,渗透系数较纯净砂减小两个数量级,并不再发生较大变化,这与本次试验现象基本一致。原状铁尾矿砂的细粒临界值应该在40%左右。这也与表1计算范围的上限基本一致。
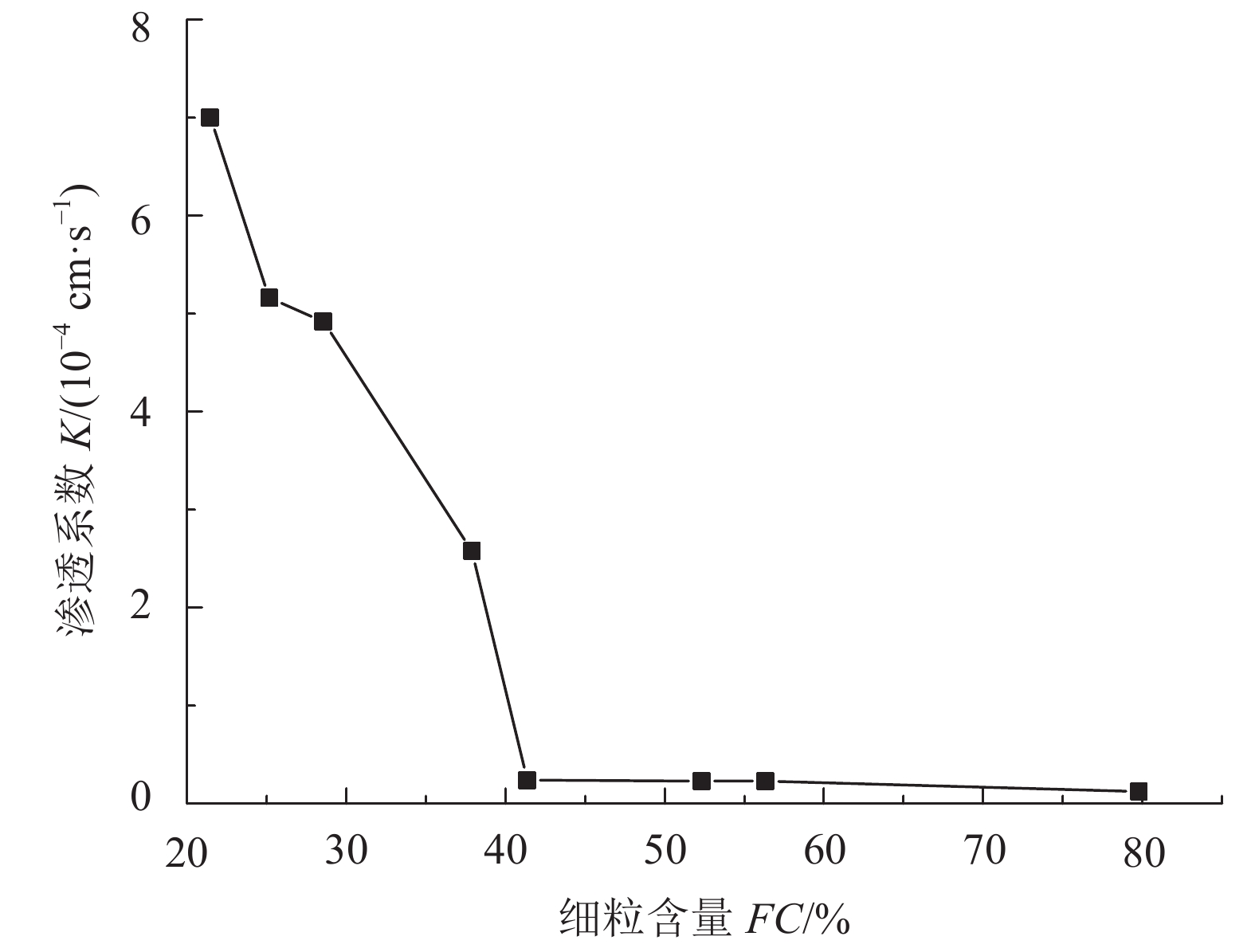 |
| 图2 渗透系数随细粒含量变化曲线 Fig. 2 Curve between K and FC |
3.2 Cu与Cc对渗透系数的影响
颗粒级配特征是影响土体渗透性的重要因素。不均匀系数Cu与曲率系数Cc是评价颗粒均匀性与连续性的重要指标。不均匀系数Cu对渗透系数的影响如图3所示。由图3可知:曲线也分为两个阶段,Cu较小时,级配不良,渗透系数随其增大迅速减小;而当Cu超过5以后,渗透系数变化减小。
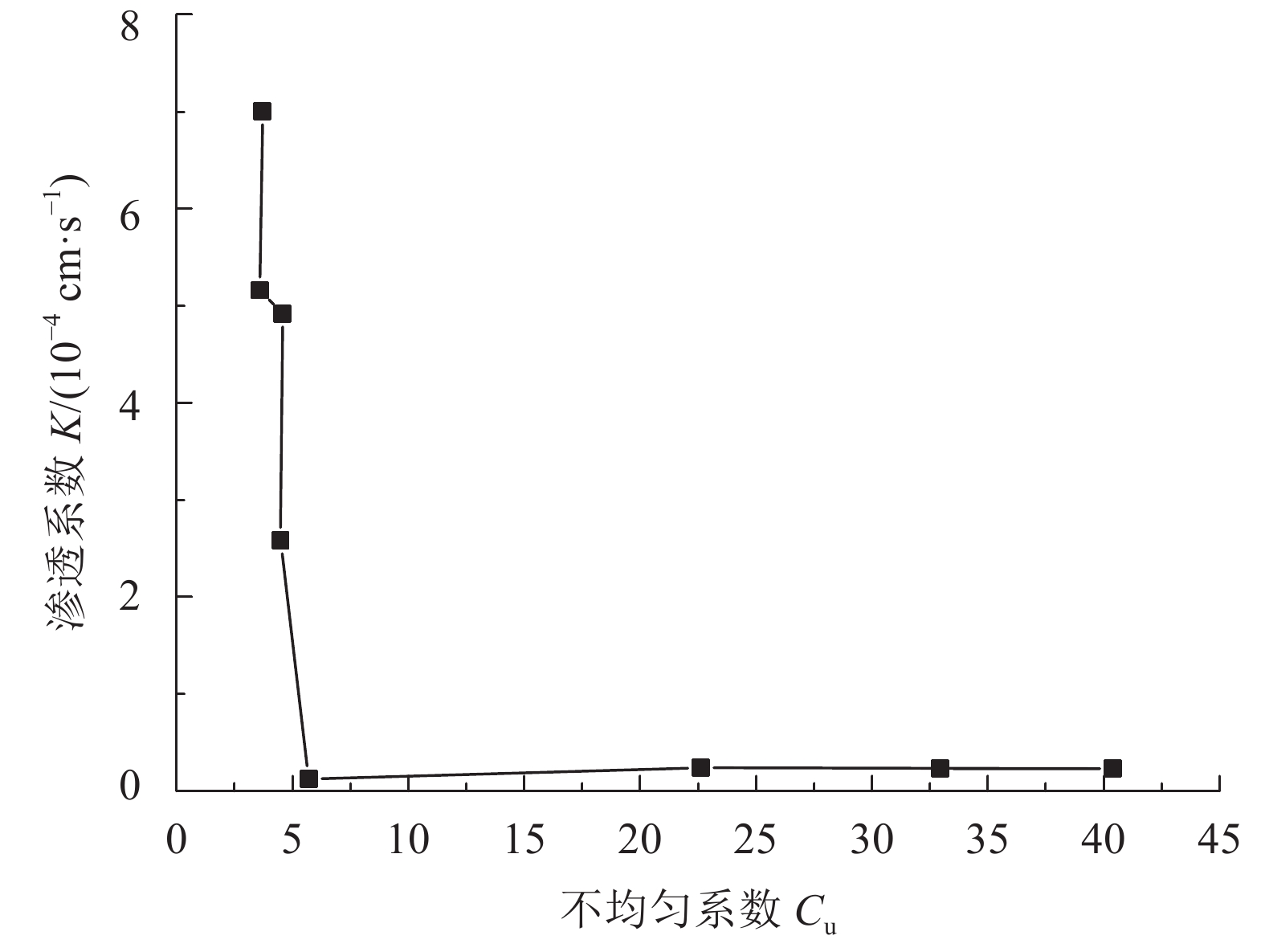 |
| 图3 渗透系数随不均匀系数变化曲线 Fig. 3 Curve between K and Cu |
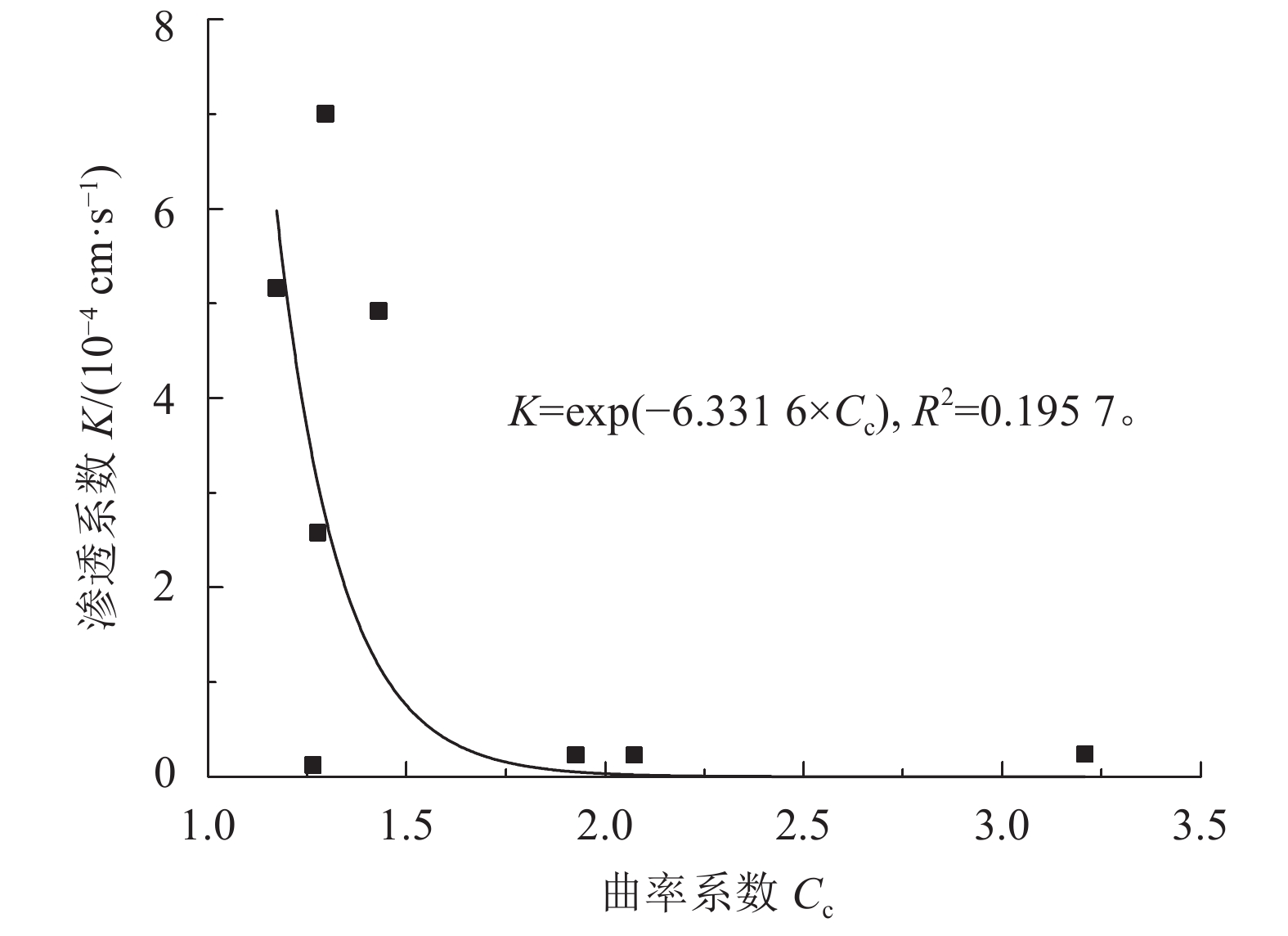
曲率系数对渗透系数的影响如图4所示。
 |
| 图4 渗透系数随曲率系数变化曲线 Fig. 4 Curve between K and Cc |
由图4可知,其变化趋势与图3相似,均是先急剧减小后变化较为平缓。
3.3 颗粒粒径与比表面积对渗透系数的影响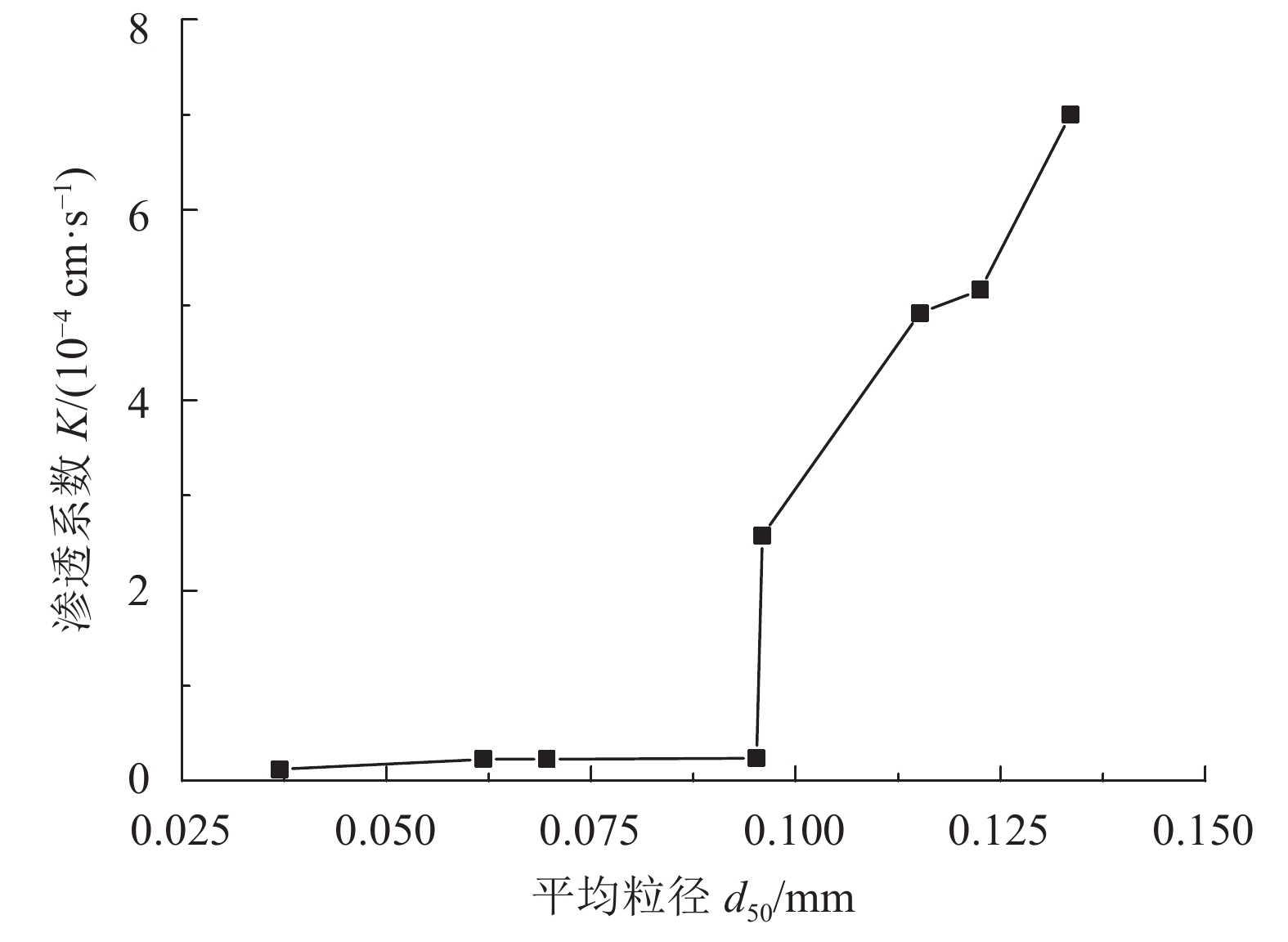 |
| 图5 渗透系数随平均粒径变化曲线 Fig. 5 Curve between K and d50 |
 |
| 图6 渗透系数随平均加权粒径变化曲线 Fig. 6 Curve between K and average weighted particle size |
由图5可知:随着平均粒径的增大,原状铁尾矿砂中的骨架颗粒增多,孔隙变大,渗透性变强。当平均粒径达到0.095 mm时,曲线出现拐点;当平均粒径小于0.095 mm时,渗透系数变化不大,呈现缓慢增长趋势;平均粒径大于0.095 mm时,渗透系数急剧增大。
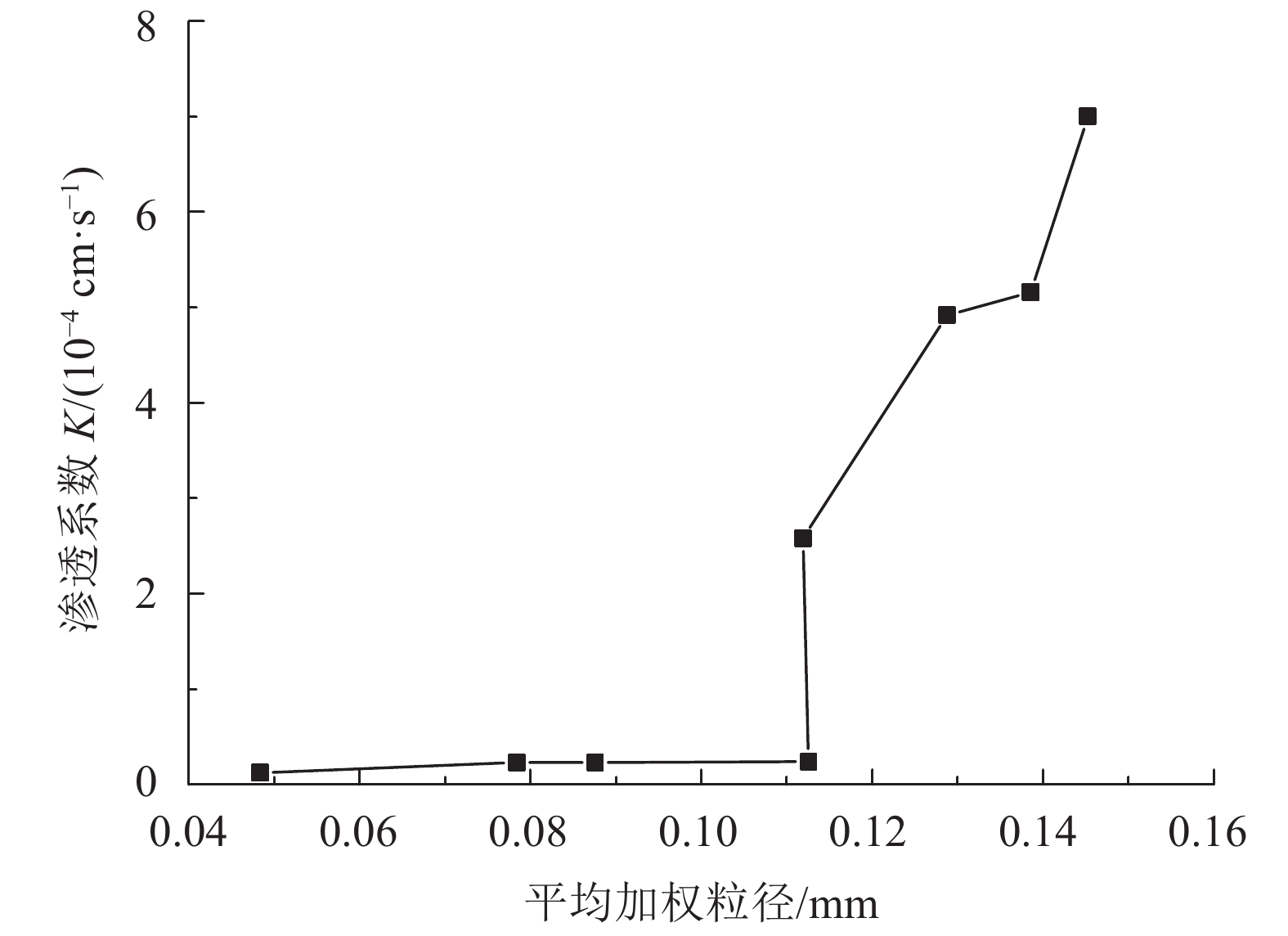
由图6可知:加权平均粒径对渗透系数的影响与平均粒径类似。当加权平均粒径小于0.11 mm时,渗透系数缓慢增长;当加权平均粒径大于0.11 mm时,渗透系数急剧增长。
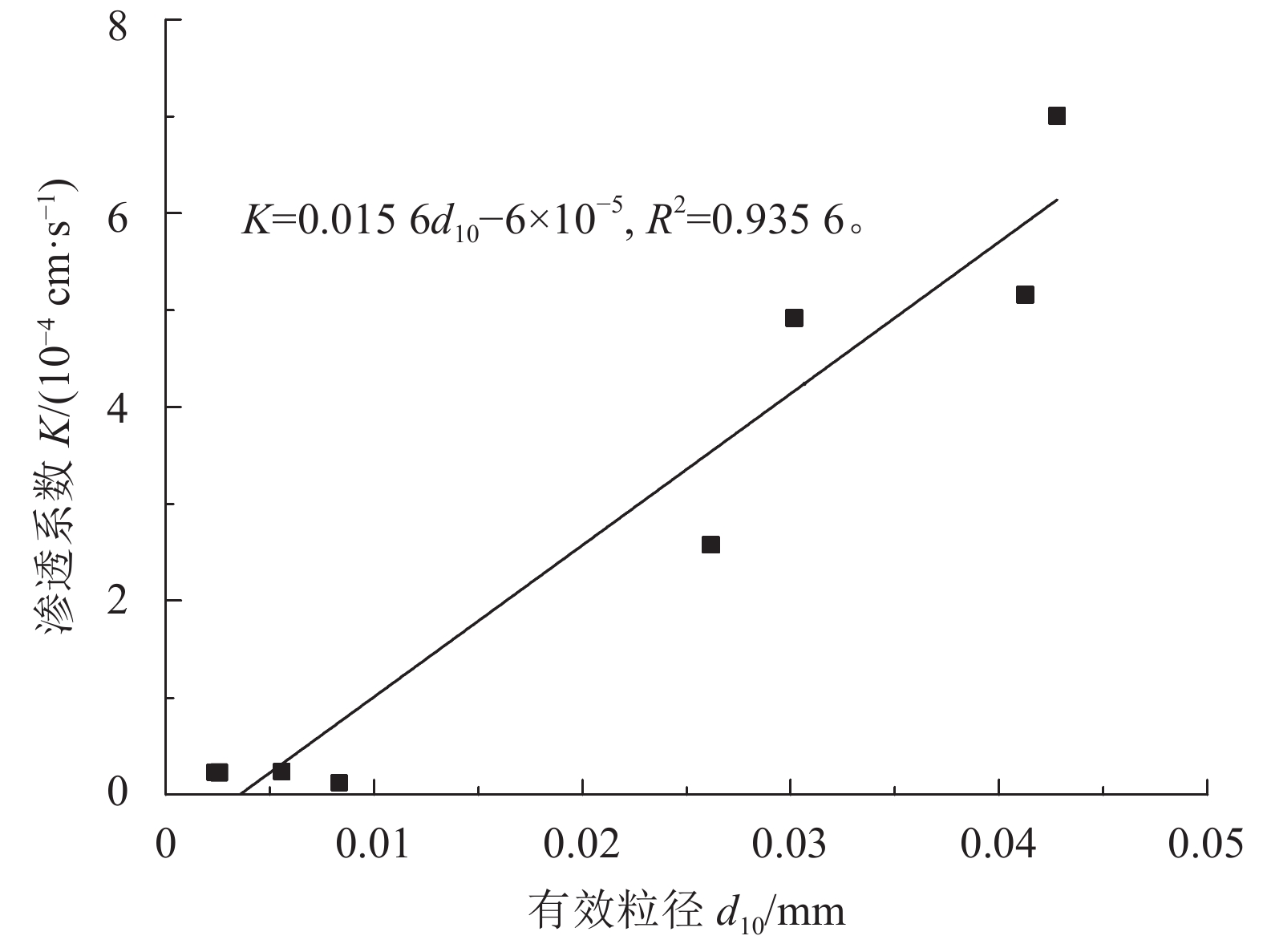
与平均粒径和加权平均粒径不同,有效粒径与渗透系数却呈现出较好的线性关系,如图7所示,渗透系数随着有效粒径的增大而不断增大,两者呈现出较高的拟合度。
 |
| 图7 渗透系数随有效粒径变化曲线 Fig. 7 Curve between K and d10 |
如图8所示,体积比表面积与渗透系数的变化趋势与图5和6相似。但是,整体变化相对平缓,没有特别明显的拐点出现。
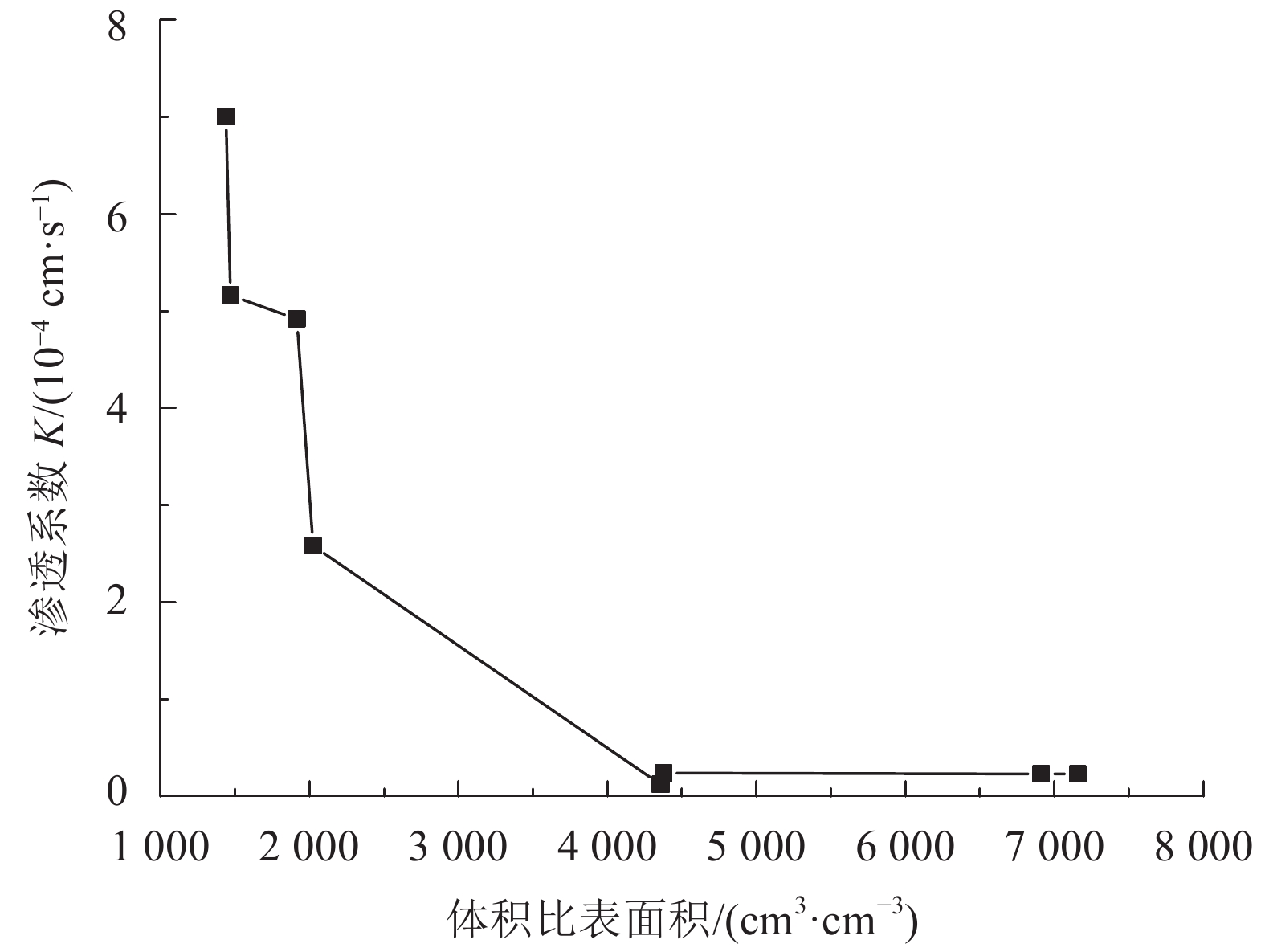 |
| 图8 渗透系数随体积比表面积变化曲线 Fig. 8 Curve between K and specific surface area |
3.4 骨架孔隙比对渗透系数的影响
渗透系数随孔隙比e变化趋势如图9所示。观察图9可知:孔隙比对渗透系数的影响主要分为3个阶段,第1个阶段,随着孔隙比的增加,渗透系数增大;第2个阶段,孔隙比虽然相近,但是渗透系数相差较大;第3个阶段,随着孔隙比的增加,渗透系数缓慢减小。
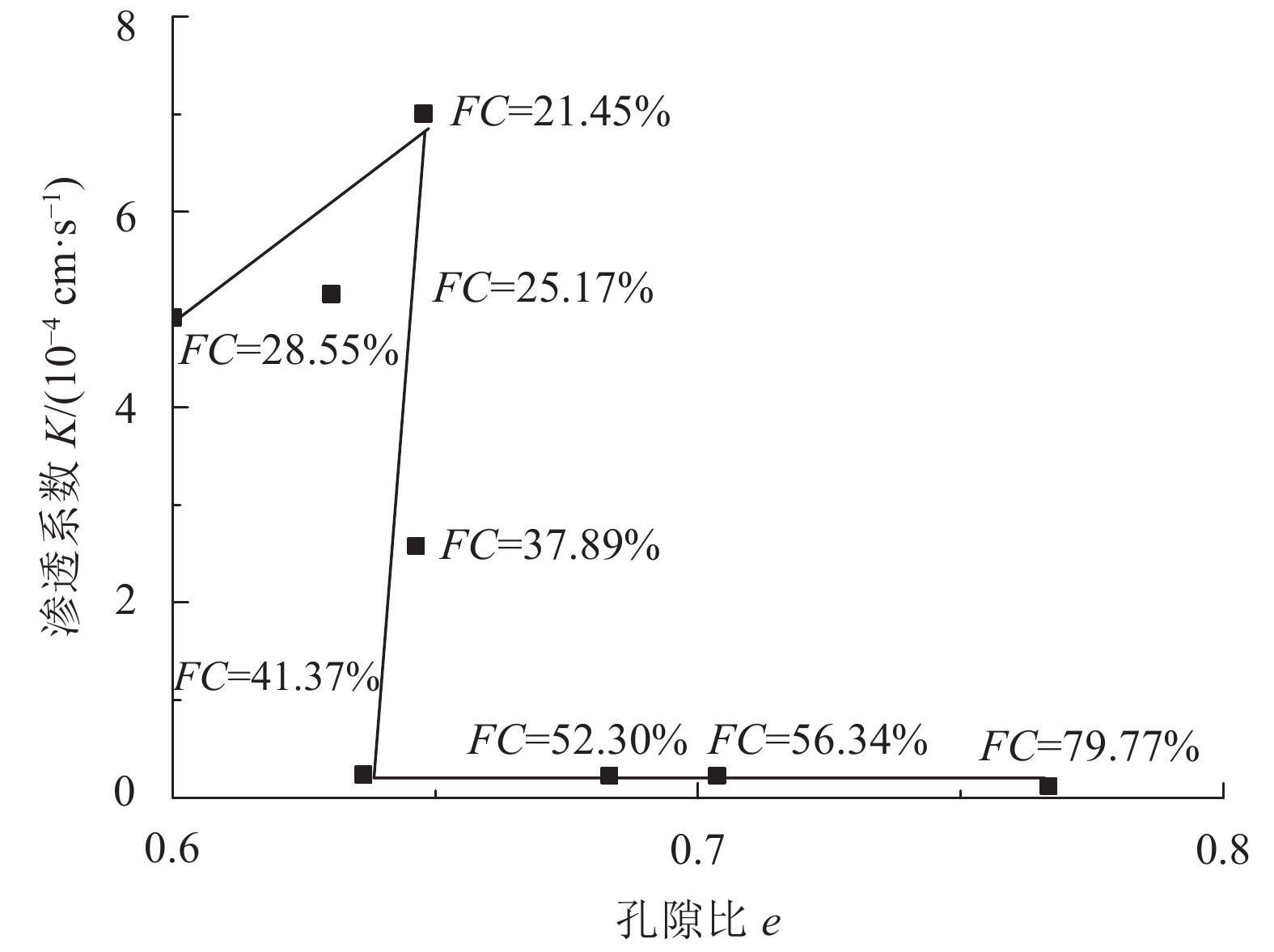 |
| 图9 渗透系数随孔隙比变化曲线 Fig. 9 Curve between K and e |
第1阶段(FC=28.55%,FC=25.17%,FC=21.45%)铁尾矿砂的细粒含量较少,细粒填充于粗粒之间的孔隙,当细粒含量减少时,孔隙比增加,渗透系数增大。
第2阶段(FC=21.45%,FC=37.89%,FC=41.37%)铁尾矿砂的细粒含量开始增多,这时其孔隙比相近,但是渗透系数却相差较大。这主要是由于细粒含量增加的过程中,孔隙比先减小后增大,所以不同的细粒含量可能会对应相近的孔隙比,图9中20%左右细粒含量的铁尾矿砂和40%左右细粒含量的铁尾矿砂对应的孔隙比相近,这与乔兰等[18]对尾矿砂性质的研究结果基本一致。虽然孔隙比相近,但是,细粒含量不同造成的孔隙尺寸并不相同。细粒含量较小时,细粒松散的填充于粗颗粒之间,此时的大孔隙较多;而细粒含量较大时,细粒将粗粒包裹,形成的小孔隙较多。虽然总孔隙比相近,但是受到孔隙尺寸的影响,造成渗透系数降低。
土体颗粒外侧均包裹一层结合水膜,这就造成有效孔隙要小于实际孔隙[19]。细粒更容易形成小孔隙,细粒含量越大,小孔隙越多。当总孔隙比相同的情况下,小孔隙更容易受到结合水膜的影响,小孔隙试样的总有效孔隙要小于大孔隙试样的总有效孔隙。进而,造成相同总孔隙比情况下,细粒含量较大的铁尾矿砂试样的渗透系数较小,而细粒含量较少的铁尾矿砂的渗透系数较大。
第3阶段(FC=41.37%,FC=52.3%,FC=56.34%,FC=79.77%)铁尾矿砂的细粒含量进一步增多。虽然总孔隙比增大,但是,此时铁尾矿砂孔隙主要由小孔隙和极小孔隙构成,受结合水膜影响,有效孔隙变小。因此,虽然总孔隙比增长,但是渗透系数受有效孔隙比影响较大,造成渗透系数随孔隙比增大而缓慢减小。
渗透系数随粒间孔隙比es变化曲线如图10所示。由图10可知,主要分为两个过程:当es小于2左右时,渗透系数随其增大而迅速下降;当es大于2左右时,渗透系数呈现缓慢下降趋势。
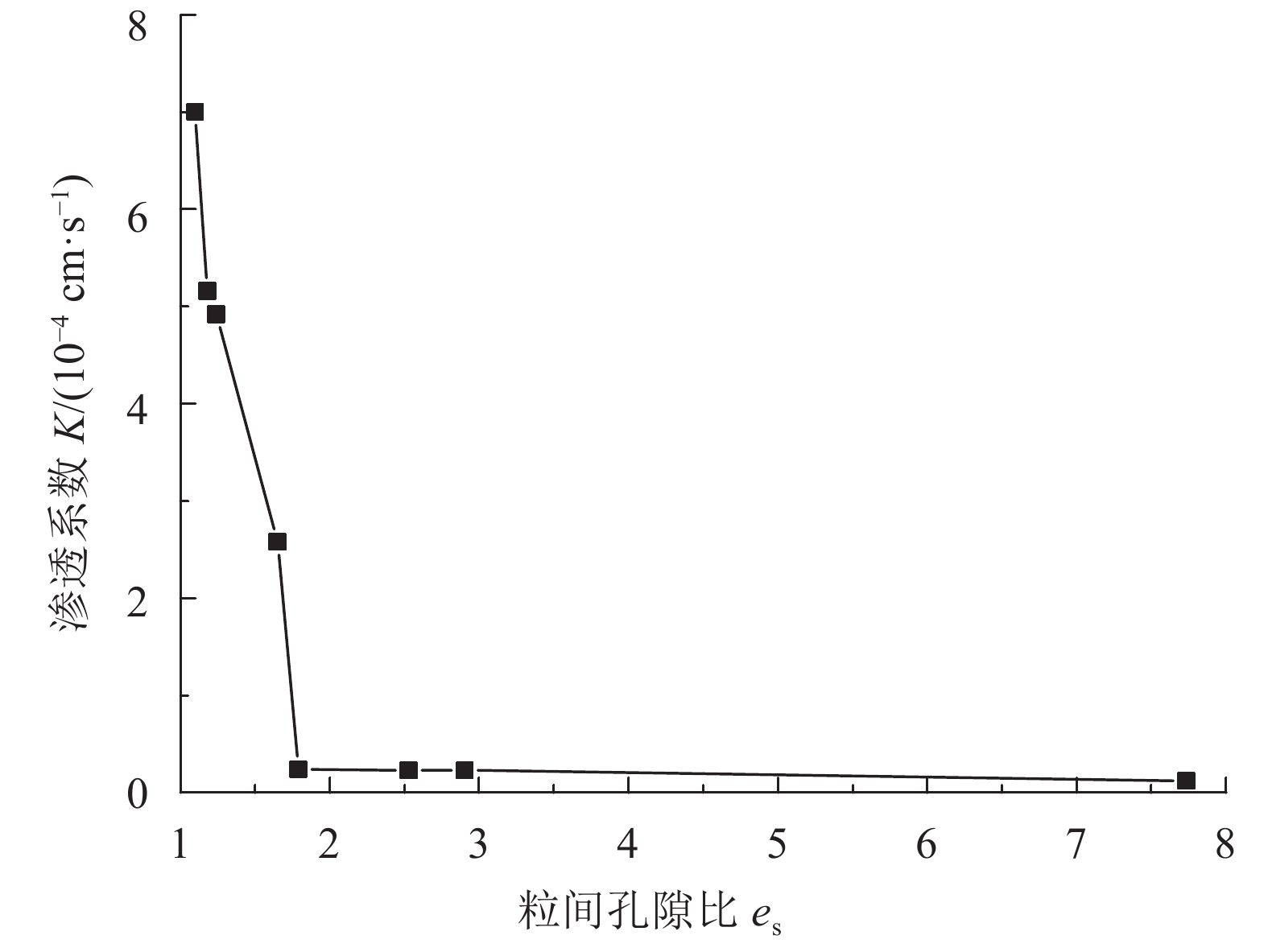 |
| 图10 渗透系数随粒间孔隙比变化曲线 Fig. 10 Curve between K and es |
渗透系数随粉粒间孔隙比ef变化曲线如图11所示。由图11可知:粉粒间孔隙比ef与渗透系数有较好的相关性,拟合度较高。渗透系数随着ef的增大而增大。细粒含量较少时,其松散的分布于粗颗粒之间,故造成ef较大;而当细粒含量较大时,细粒包裹粗粒,细粒之间有序排列,故造成ef减小。所以,渗透系数虽然受到细粒含量的影响,但是,没有出现剧烈变化的拐点。两者呈现较好的线性相关性。
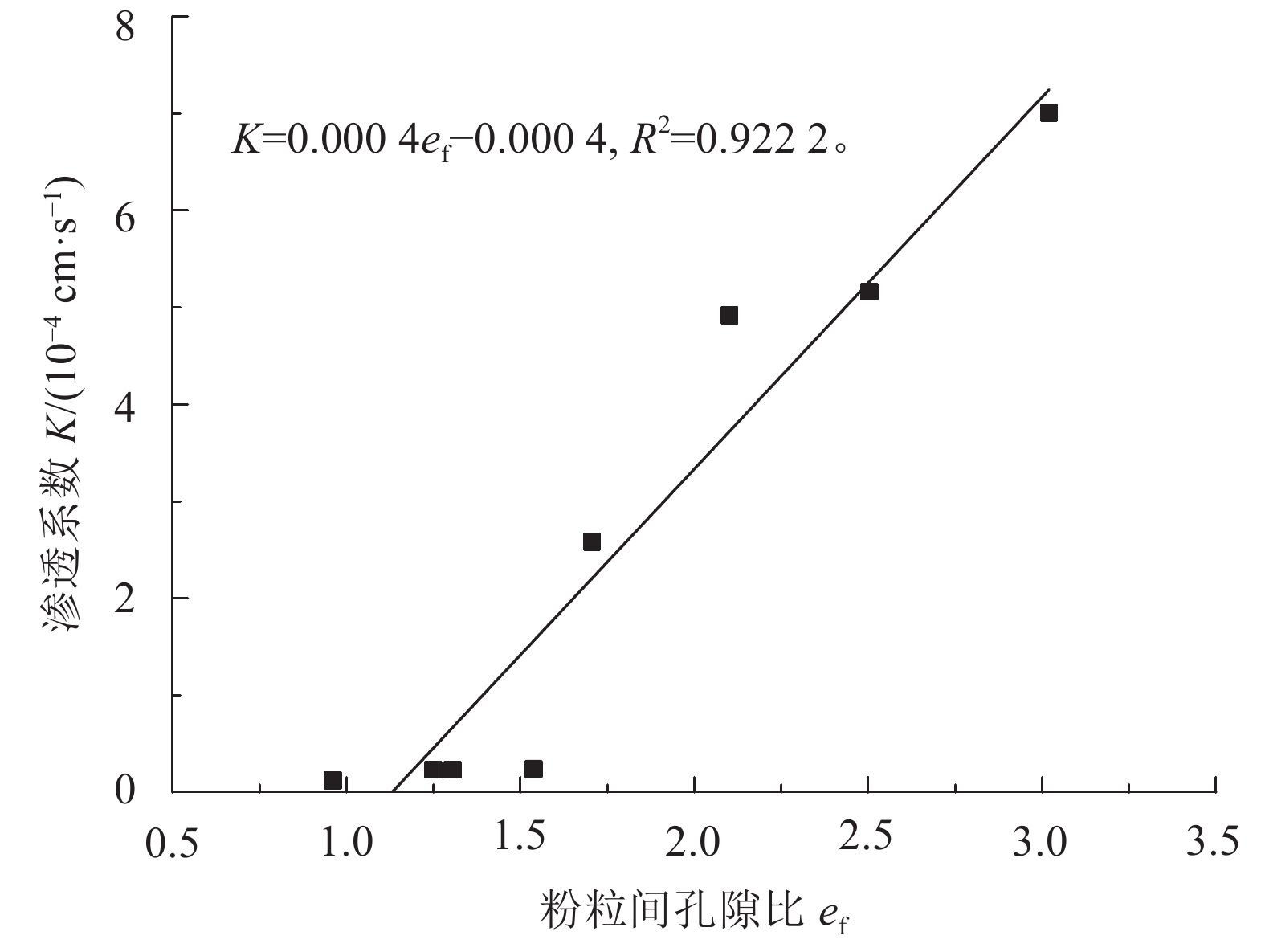 |
| 图11 渗透系数随粉粒间孔隙比变化曲线 Fig. 11 Curve between K and ef |
4 渗透系数计算公式的讨论
渗透性问题一直是岩土工程研究的重要课题,而渗透系数是表征渗透特性最重要的指标,其变化特性直接关系到工程的安全性。国内外学者均对渗透系数进行了广泛的研究,以期建立渗透系数的计算公式。国外学者通过开展大量渗透性研究,提出了众多渗透系数计算公式,其中,比较著名的有太沙基公式[20]、哈增公式[21]、柯森公式[22]等。国内学者也对渗透系数进行了大量研究,朱崇辉[23]、张宜健[24]从砂土级配特征等角度着手,提出了各自的渗透系数计算公式。如式(5)~(9)所示。但是,哈增公式只考虑了粒径一个因素;太沙基公式与柯森公式只考虑了孔隙比与粒径对渗透系数的影响,没有考虑级配等因素的影响;国内学者提出的渗透系数计算公式虽然考虑了较多因素,但其均是基于特定砂土,对其他特殊砂土(如铁尾矿砂)渗透系数计算的准确性尚不明确。同时,由于细粒含量变化后,孔隙结构特征也会发生变化,上述公式没有体现细粒含量的影响。
太沙基(Terzaghi)公式如下:
| $K = 2d_{10}^2{e^2}$ | (5) |
哈增(Hazen)公式如下:
| $K = 2d_{10}^2$ | (6) |
柯森(Kozeny)公式如下:
| $K = 780\frac{{{n^3}}}{{{{(1 - n)}^2}}}d_9^2$ | (7) |
张宜健公式如下:
| $K = 157\frac{{{n^3}}}{{{{(1 - n)}^2}}}{C_{\rm{u}}}{C_{\rm{c}}}d_{10}^2$ | (8) |
朱崇辉公式如下:
| $K = 4e{C_{\rm{u}}}{C_{\rm{c}}}d_{10}^2$ | (9) |
式中:K为20 ℃时试样土体的渗透系数;n为试样土体孔隙率;e为试样土体孔隙比;d9、d10、d20分别为累计含量为达到9%、10%、20%时对应的试样土体颗粒直径,mm;Cc为试样土体的曲率系数;Cu为试样土体的不均匀系数。
本文从细粒含量FC、级配、粒径、比表面积和粉粒间孔隙比等多个角度出发,对铁尾矿砂原状样的渗透性质进行了分析。结果表明,受细粒含量的影响,原状铁尾矿砂的渗透系数随不均匀系数Cu、曲率系数Cc、平均粒径、加权平均粒径、体积比表面积和粒间孔隙比es变化时,均会出现剧烈变化的拐点,在经过拐点后,变化趋势趋于平缓。说明以上几种因素在经过拐点后,其对铁尾矿砂的渗透系数变化影响较小,即对细粒含量较大时铁尾矿砂的渗透系数变化不敏感,相关性较低。但是,有效粒径和粉粒间孔隙比与铁尾矿砂的渗透系数呈现出了较好的相关性。以粉粒间孔隙比和有效粒径为参量对铁尾矿砂的渗透系数进行预测。建立铁尾矿砂渗透系数预测公式,并进行了温度修正,公式如下:
| $K = R\frac{{{\eta _{20}}}}{{{\eta _T}}}{e_{\rm{f}}}{d_{10}}$ | (10) |
式中,R为无因次系数。
将试验中实际测得的试验数据代入建立的计算式(10)中进行反演验算,可以得出公式中无因次系数R值。经过计算得到当R取5.5×10–2时渗透系数的计算值与实际的测量值最接近。故本次R取5.5×10–2,应用式(10)对渗透系数进行计算,并与传统公式进行对比,结果如表2所示。
| 表2 不同细粒含量铁尾矿砂渗透系数计算值与实测值对比 Tab. 2 Comparison between measured values and predictive results of hydraulic conductivity using different state parameters for iron tailings sand with different fines content |
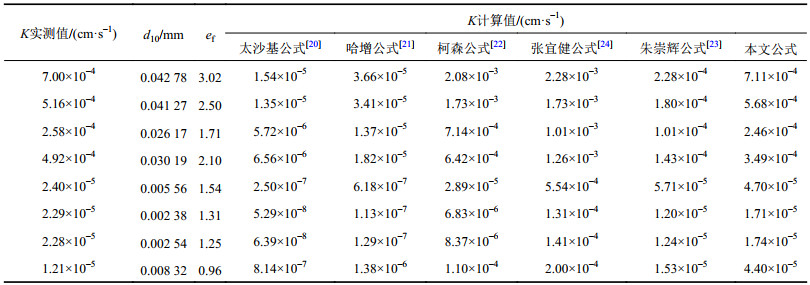 |
观察表2可知:太沙基公式、哈增公式、柯森公式、张宜健公式的计算结果与实测值相差较大,均相差1~3个数量级,并不适用于铁尾矿砂的渗透系数计算。应用朱崇辉公式对铁尾矿砂渗透系数进行计算,结果相对准确,但是,计算结果与实测值也相差几倍。而应用本文公式对铁尾矿砂渗透系数进行计算,结果较为准确,与实测值均保持同一个数量级,且数值相差不大。这对陈坑尾矿坝的渗流场分析与稳定性计算具有一定意义。同时,所取尾矿砂试样主要为磁铁矿尾砂,这对类似的铁尾砂渗透性计算也有一定借鉴意义。但是,不同种类铁尾矿砂的成分并不相同,其不同成分对其渗透系数计算可能会造成一定影响,这有待进一步研究。
5 结 论1)原状铁尾矿砂的渗透系数受细粒含量影响明显,当细粒含量小于40%左右时,渗透系数随细粒含量的增加而快速下降;当细粒含量大于40%左右时,渗透系数呈现缓慢下降的趋势,并趋向于稳定值。
2)原状铁尾矿砂的渗透系数与不均匀系数Cu、曲率系数Cc、平均粒径、加权平均粒径、体积比表面积和粒间孔隙比es之间呈现明显的非线性关系,难以表征细粒含量较大时的渗透系数变化。但是,有效粒径和粉粒间孔隙比与铁尾矿砂的渗透系数呈现出了较好的相关性。可以使用粉粒间孔隙比和有效粒径为参量对铁尾矿砂的渗透系数进行预测。
3)应用太沙基公式、哈增公式、柯森公式、张宜健公式和本文提出的公式对原状铁尾矿砂渗透系数进行计算,计算结果与实测值相差较大,应用朱崇辉公式对铁尾矿砂渗透系数进行计算,结果相对准确,但是,计算结果与实测值也相差几倍。应用本文提出的计算公式对原状铁尾矿砂渗透系数进行计算,结果较为准确。
4)本文对原状铁尾矿砂的渗透特性进行了分析,对铁矿类尾矿坝的渗流作用下的稳定性分析具有一定意义。但是,对铁尾矿砂物质成分与微观尺度下的渗透特性没有进行分析,相关研究工作还有待进一步开展。
| [1] |
Hartog N,Stuyfzand P. Water quality considerations on the rise as the use of managed aquifer recharge systems widens[J]. Water, 2017, 9(10): 808. DOI:10.3390/w9100808 |
| [2] |
Naeini S A,Baziar M H. Effect of fines content on steady-state strength of mixed and layered samples of a sand[J]. Soil Dynamics and Earthquake Engineering, 2004, 24(3): 181-187. DOI:10.1016/j.soildyn.2003.11.003 |
| [3] |
Zhu Jianqun.Strength properties and steady-state behavior of sandy soil[D].Wuhan:Institute of Rock and Soil Mechanis,Chinese Academy of Sciences,2007. 朱建群.含细粒砂土的强度特征与稳态性状研究[D].武汉:中国科学院武汉岩土力学研究所,2007. |
| [4] |
Yin J H. Properties and behaviour of Hong Kong marine deposits with different clay contents[J]. Canadian Geotechnical Journal, 1999, 36(6): 1085-1095. DOI:10.1139/t99-068 |
| [5] |
Al–Shayea N A. The combined effect of clay and moisture content on the behavior of remolded unsaturated soils[J]. Engineering Geology, 2001, 62(4): 319-342. DOI:10.1016/s0013-7952(01)00032-1 |
| [6] |
Liu Xuezhu,Chen Guoxing. Experimental study on influence of clay particle content on liquefaction of Nanjing fine sand[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(3): 150-155. [刘雪珠,陈国兴. 粘粒含量对南京粉细砂液化影响的试验研究[J]. 地震工程与工程振动, 2003, 23(3): 150-155. DOI:10.13197/j.eeev.2003.03.024] |
| [7] |
Zeng Changnv.Laboratory test study on the influence of percent fines on silt liquefaction and post-liquefaction[D].Nanjing:Hohai University,2006. 曾长女.细粒含量对粉土液化及液化后影响的试验研究[D].南京:河海大学,2006. |
| [8] |
Phan V T A,Hsiao D H,Nguyen P T L. Critical state line and state parameter of sand-fines mixtures[J]. Procedia Engineering, 2016, 142: 299-306. DOI:10.1016/j.proeng.2016.02.045 |
| [9] |
Zhang Chao,Yang Chunhe. Effect of fines content on liquefaction properties of tailings material[J]. Rock and Soil Mechanics, 2006, 27(7): 1133-1137. [张超,杨春和. 细粒含量对尾矿材料液化特性的影响[J]. 岩土力学, 2006, 27(7): 1133-1137. DOI:10.3969/j.issn.1000-7598.2006.07.023] |
| [10] |
Xu Zengguang,Yang Xuemin,Chai Junrui. Analysis of permeability coefficient of tailings considering the chemical clogging processes[J]. Hydrogeology & Engineering Geology, 2016, 43(4): 26-29. [许增光,杨雪敏,柴军瑞. 考虑化学淤堵作用的尾矿砂渗透系数变化规律研究[J]. 水文地质工程地质, 2016, 43(4): 26-29. DOI:10.16030/j.cnki.issn.1000-3665.2016.04.05] |
| [11] |
Zhang Yuan,Zhang Bing,Liang Bing,et al. Study on the effect of acid and alkali solution on the permeability of sulfur-containing tailings[J]. Non-Metallic Mines, 2017, 40(6): 48-50. [张媛,张兵,梁冰,等. 酸碱溶液对含硫尾矿砂渗透特性的影响研究[J]. 非金属矿, 2017, 40(6): 48-50. DOI:10.3969/j.issn.1000-8098.2017.06.015] |
| [12] |
Zeng Sheng,Ji Kun,Li Jun,et al. Numerical simulation of the influence of structural features of tailings on its permeability[J]. Metal Mine, 2017(1): 43-46. [曾晟,吉坤,李军,等. 尾矿砂结构特征对渗透性影响的数值模拟[J]. 金属矿山, 2017(1): 43-46. DOI:10.3969/j.issn.1001-1250.2017.01.009] |
| [13] |
Mi Yujuan.Experimental study on permeability of Fengshuigou tailing sand and its seepage simulation[D].Anshan:University of Science and Technology Liaoning,2018. 弭玉娟.风水沟尾矿砂渗透性试验研究与渗流模拟[D].鞍山:辽宁科技大学,2018. |
| [14] |
Thevanayagam S. Effect of fines and confining stress on undrained shear strength of silty sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(6): 479-491. DOI:10.1061/(asce)1090-0241(1998)124:6(479) |
| [15] |
Thevanayagam S,Martin G R. Liquefaction in silty soils—Screening and remediation issues[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(9/10/11/12): 1035-1042. DOI:10.1016/s0267-7261(02)00128-8 |
| [16] |
Rahman M M,Lo S R,Gnanendran C T. On equivalent granular void ratio and steady state behaviour of loose sand with fines[J]. Canadian Geotechnical Journal, 2008, 45(10): 1439-1456. DOI:10.1139/t08-064 |
| [17] |
Nagaraj T S,Pandian N S,Narasimha R. An approach for prediction of compressibility and permeability behavior of sand-bentonite mixes[J]. Indian Geotechnical Journal, 1991, 21(3): 271-282. |
| [18] |
Qiao Lan,Qu Chunlai,Cui Ming. Effect of fines content on engineering characteristics of tailings[J]. Rock and Soil Mechanics, 2015, 36(4): 923-927. [乔兰,屈春来,崔明. 细粒含量对尾矿工程性质影响分析[J]. 岩土力学, 2015, 36(4): 923-927. DOI:10.16285/j.rsm.2015.04.002] |
| [19] |
Dang Faning,Liu Haiwei,Wang Xuewu,et al. Empirical formulas of permeability of clay based on effective pore ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1909-1917. [党发宁,刘海伟,王学武,等. 基于有效孔隙比的黏性土渗透系数经验公式研究[J]. 岩石力学与工程学报, 2015, 34(9): 1909-1917. DOI:10.13722/j.cnki.jrme.2014.1583] |
| [20] |
卡尔·太沙基,劳尔夫·皮·帕克.工程实用土力学[M].蒋彭年,译.北京:水利电力出版社,1960.
|
| [21] |
Hazen A.Discussion of “dams on sand foundation” by A. C. Koenig[J].Transactions American Society of Civil Engineers,1911,73:199–203.
|
| [22] |
米切尔 J K.岩土工程土性分析原理[M].高国瑞,韩选江,译.南京:南京工学院出版社,1988.
|
| [23] |
Zhu Chonghui.Study on the coarse-grained soil permeability characteristic[D].Yangling:Northwest A & F University,2006. 朱崇辉.粗粒土的渗透特性研究[D].杨凌:西北农林科技大学,2006. |
| [24] |
Zhang Yijian.Investigation on permeability of sands with different particle size[D].Xi’an:Xi’an University of Architecture and Technology,2013. 张宜健.不同粒径级砂性土渗透特性试验研究[D].西安:西安建筑科技大学,2013. |
 2020, Vol. 52
2020, Vol. 52


