地面试验设备对高超声速技术的发展十分重要,其中包含长时间风洞(如Langley中心的2.44 m高温风洞)和短时风洞(如中国空气动力研究与发展中心(CARDC)的Φ2.4 m脉冲风洞)。鉴于长时间风洞试验费用高昂,激波风洞和脉冲风洞等短时风洞对高超声速技术发展的作用变得尤为突出。不同于低速、长时间风洞,对于高超声速短时风洞,风洞冲击作用引起的模型振动在试验时间内无法消除,这给天平测力带来严重的干扰,极大地增加了测力的难度,因此,试验过程中模型气动力载荷的测量成为该类试验的关键技术之一。
为解决激波风洞和脉冲风洞快速测力的难题,国内外学者进行了大量的研究,主要包括加速度计天平[1-4]、应力波天平[5-6]、压电天平[7]、应变天平[8-11]等。研究表明,针对脉冲燃烧风洞,测力系统采用应变天平更为合适,这是因为该类风洞有效试验时间超过100 ms,若天平刚度过低,则试验过程中模型姿态变化较大,不利于气动力载荷的测量,而对于压电天平,难以达到测量精度要求。Wang等[8]设计了杆式和盒式应变天平,并在JF–12激波风洞进行了气动力载荷测量试验,该风洞试验时间可达100 ms。贺伟等[9]对比了脉冲燃烧风洞和长时间风洞测力结果,验证了单分量测力天平的脉冲风洞测力方法。吕金洲等[10-11]推导了测力系统的动力学方程,采用有限元方法和试验结果验证了惯性补偿方法。刘洪山等[12]总结了应力波天平在国内激波风洞上的应用。
以上研究或采用应变测力天平进行了短时风洞试验模型气动力载荷测量,或对天平输出误差进行了分析,但天平刚度对测力系统输出结果的影响并未进行研究。因此,作者基于惯性补偿方法[12],研究了天平刚度对测力系统的输出结果的影响。
1 测力系统概述简化试验测力系统主要由试验模型、测力天平和支架3部分组成,为降低研究的复杂性,对试验模型进行了简化。
图1为测力天平,主要由浮动框、固定框、测量元件、支撑梁和惠斯顿电路组成。
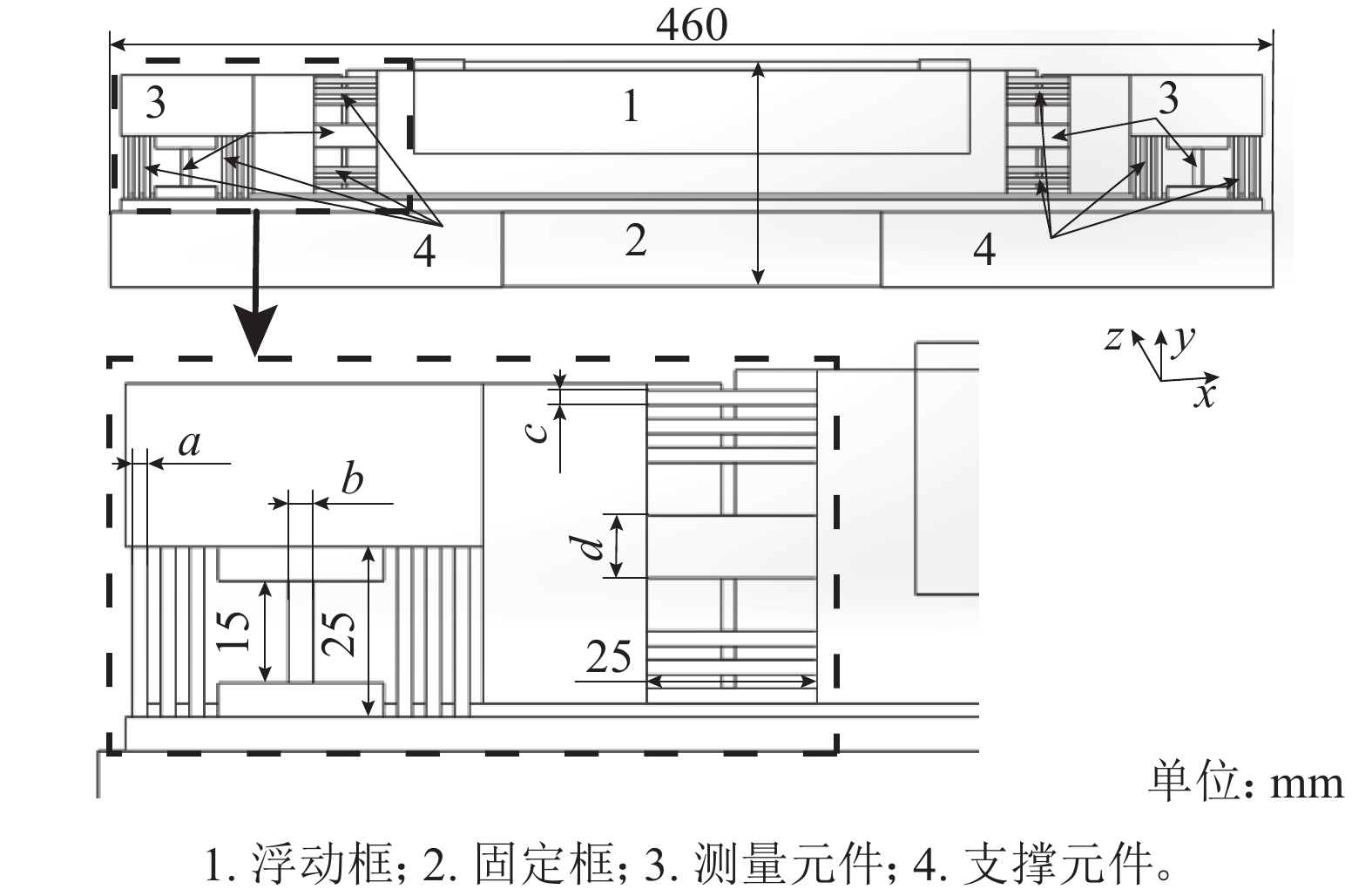 |
| 图1 测力天平 Fig. 1 Force balance |
图1中下面部分为测量元件及支撑梁参数,a、b、c、d分别为天平竖向支撑元件、轴向测量元件、横向支撑元件、法向和俯仰力矩测量元件的尺寸。根据研究需要,设计了3种不同刚度的测力天平,分别记为天平A、B、C,对于以上3台测力天平,其竖向支撑元件a的厚度分别为1.50、1.85和2.20 mm,轴向测量元件b的厚度分别为3.6、4.3和5.0 mm,横向支撑元件c的厚度分别为1.50、1.85和2.20 mm,法向和俯仰力矩测量单元厚度分别为5.0、7.1、9.2 mm。
从以上数据可知,测力天平A、B、C的刚度依次升高,分别将安装上述天平的测力系统记为FMS–A、FMS–B和FMS–C。试验过程中,气动力载荷使天平测量元件产生变形,惠斯顿电路输出电压发生改变,从而根据天平输出电压和标定公式计算模型所受到的气动力载荷。
2 测力系统动力学建模测力系统简化结果如图2所示,试验模型简化为一个具有较高刚度的实体结构,模型支架刚度很高,可视为刚体。对于试验测力系统,天平浮动框与试验模型固连,视为整体;天平固定框与模型支架固连,同样视为整体。试验过程中,测力系统应变量最大的部位为天平测量元件和支撑元件,因此测力系统可进一步简化为如图2所示的梁–弹簧–阻尼系统。图2中:试验模型和天平浮动框简化为梁m;模型支架和天平固定框简化为地面;天平测量元件简化为3分量弹簧k1和k2,由天平前后对称性可知,k1x、k1y和k1Mz分别等于k2x、k2y和k2Mz;c1和c2为测力系统的阻尼。获得测力系统动力学方程为:
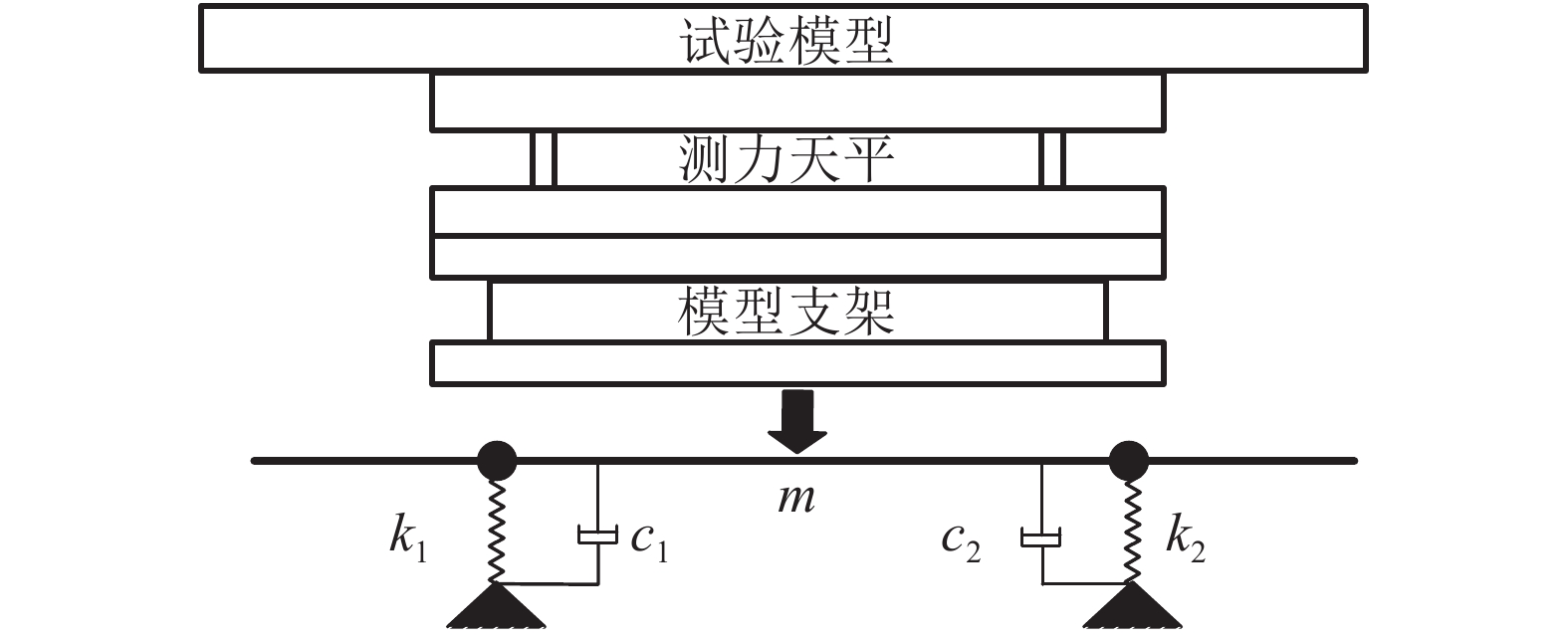 |
| 图2 测力天平简化模型 Fig. 2 Simplified model of the force measurement balance |
| $ {{{{M}}{{\ddot q}} + {{C}}{{\dot q}} + {{Kq}} = {{F}}}} $ | (1) |
式中,M、C和K分别为测力系统质量、阻尼和刚度矩阵,q和F分别为测力系统的位移和载荷向量。从式(1)可知,试验过程中模型受到的气动力载荷为天平弹性力、系统阻尼和模型惯性力之和,但由于系统阻尼很小,分析时忽略了阻尼输出,仅考虑系统弹性力和惯性力输出。
2.1 测力系统虚拟标定计算测力系统的弹性输出结果,需获得其刚度矩阵K,因此需对其进行虚拟标定。
测力天平应变计位置如图3(a)所示。
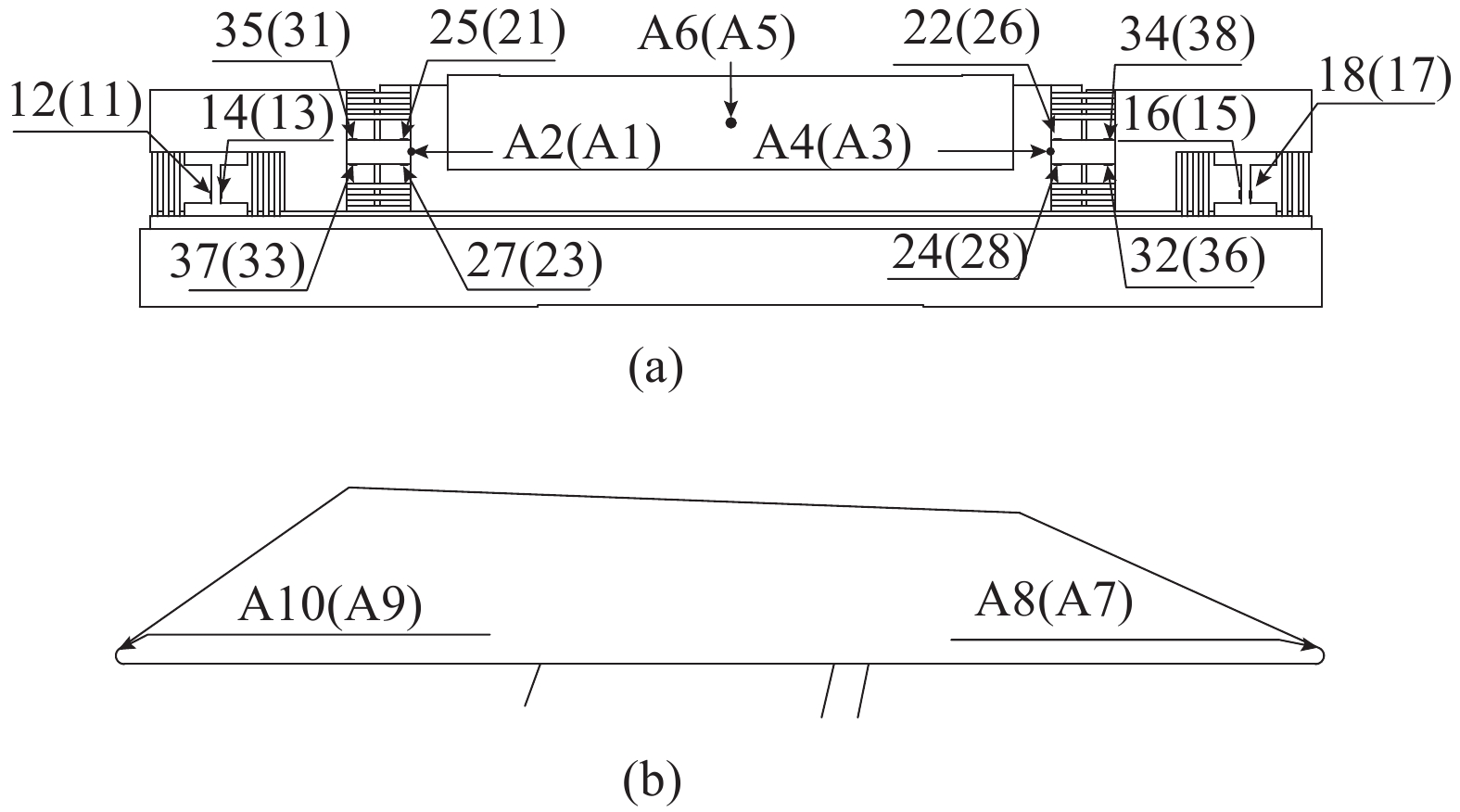 |
| 图3 测力天平应变计位置 Fig. 3 Strain gauge positions of the force balance |
图3(a)中:测点11~18为推力测点,输出y向应变,结果记为μ11~μ18;测点21~28为升力测点,输出x向应变,结果记为μ21~μ28;测点31~38为俯仰力矩测点,输出x向应变,结果记为μ31~μ38。测力系统的静态公式如下:
| $ {{F}} = {{U}} {{K}} $ | (2) |
式中,
向量F中,Fx、Fy和Mz分别为模型所受到的推力、升力和俯仰力矩。向量Y中,k11、k22和k33为刚度矩阵的主系数,k12、k13、k21、k23、k31和k32为干扰系数。
对式(2)进行矩阵变换可得:
| $ {{K}} = {{{U}}^{ - 1}} {{F}} $ | (3) |
因此,要获得测力系统的刚度矩阵K,需对其施加3个不相关的载荷,分别获得相应的应变结果,代入式(3)进行求解。
在测力系统的有限元模型中,试验模型和支架网格一致,测力天平支撑梁和测量元件存在一定差异,两者均进行了加密,FMS–A包含179 859个节点和32 112个单元,FMS–B包含137 833个节点和23 192个单元,FMS–C包含237 422个节点和46 085个单元,三者均采用六面体单元Solid186进行划分。各部分材料及相关参数如表1所示。加载位置为模型外表面;输入载荷分别为F1 =[–2 000,0,0]T,F2 =[0,3 000,0]T,F3 =[0,0,1 000]T,单位N;边界条件为支架下表面固定。
| 表1 测力系统各部分材料参数 Tab. 1 Material Parameters of each part of the FMS |
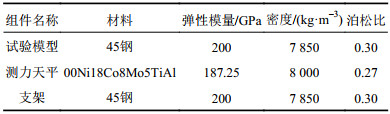 |
对于FMS–A、FMS–B和FMS–C,仿真获得相应的应变矩阵,通过式(3)获得三者的刚度矩阵分别为:
| $ {{{K}}_{\rm{A}}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} { - 0.971\;6}&{7.82 \times {{10}^{ - 5}}}&{ - 7.06 \times {{10}^{ - 3}}} \\ { - 1.78 \times {{10}^{ - 4}}}&{2.415\;4}&{2.902 \times {{10}^{ - 4}}} \\ { - 4.51 \times {{10}^{ - 3}}}&{5.14 \times {{10}^{ - 4}}}&{ - 0.492\;8} \end{array}}\!\!\!\! \right], $ |
| $ {{{K}}_{\rm{B}}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} { - 1.642\;2}&{ - 4.84 \times {{10}^{ - 4}}}&{ - 0.060\;94} \\ {4.353 \times {{10}^{ - 4}}}&{6.072\;64}&{0.182} \\ {0.020\;425}&{ - 1.631 \times {{10}^{ - 3}}}&{ - 1.168\;3} \end{array}} \!\!\!\!\right], $ |
| $ {{{K}}_{\rm{C}}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} { - 2.578\;0}&{ - 1.48 \times {{10}^{ - 4}}}&{ - 0.023\;8} \\ {1.11 \times {{10}^{ - 3}}}&{8.547\;04}&{ - 3.39 \times {{10}^{ - 3}}} \\ {0.050\;63}&{ - 4.08 \times {{10}^{ - 3}}}&{ - 1.767\;8} \end{array}} \!\!\!\!\right]{\text{。}}\!\!\!\!\! $ |
在KA、KB和KC中,k13和k31远大于其他干扰系数,说明对于测力系统的弹性输出结果,推力和俯仰力矩间的干扰较为严重;其他干扰系数非常小,说明测力系统升力和推力或俯仰力矩间的干扰较小。对比KA、KB、KC可知,主系数的绝对值依次增大,说明FMS–A、FMS–B、FMS–C的刚度依次增大。
2.2 惯性载荷试验过程中模型必然存在弹性变形,要精确获得其惯性输出载荷十分困难。测力系统轴向和俯仰方向振动模态主要为天平浮动框和试验模型的振动,法向振动模态不仅包含试验模型、天平浮动框的振动,还包含浮动框和固定框连接件,计算得测力系统质量矩阵M为:
| $ {{M}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {{m_x}}\!\!\!\!&\!\!\!\!{}\!\!\!\!&\!\!\!\!{} \\ {}\!\!\!\!&\!\!\!\!{{m_y}}\!\!\!\!&\!\!\!\!{} \\ {}\!\!\!\!&\!\!\!\!{}&\!\!\!\!{{J_{\textit{z}}}} \end{array}}\!\!\!\! \right]{\rm{ = }}\left[\!\!\!\! {\begin{array}{*{20}{c}} {210.364}\!\!\!&\!\!\!{}\!\!\!&\!\!\!{} \\ {}\!\!\!&\!\!\!{201.861}\!\!\!&\!\!\!{} \\ {}\!\!\!&\!\!\!{}\!\!\!&\!\!\!{28.536} \end{array}}\!\!\!\! \right] $ | (4) |
式中,mx、my为轴向和法向振动的质量,Jz为模型绕z轴旋转的转动惯量。
为了尽可能准确获得模型的惯性载荷,选取了10个加速度点,位置如图3所示。
A1~A6位于天平上,A7~A10位于模型上,根据以上测点加速度获得测力系统的加速度
| $ {{A}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {{a_x}} \\ {{a_y}} \\ {{a _{{M_{\textit{z}}}}}} \end{array}} \!\!\!\! \right] = \left[\!\!\!\! {\begin{array}{c} {\dfrac{1}{{10}}(A{1_x} + A{2_x} + \cdots + A{{10}_x})} \\ {\dfrac{1}{{10}}(A{1_y} + A{2_y} + \cdots + A{{10}_y})} \\ {\dfrac{1}{{4 \times 0.708}}(A{7_y} + A{8_y} + A{9_y} + A{{10}_y})} \end{array}}\!\!\!\! \right] $ | (5) |
从而,获得测力系统的惯性输出载荷为:
| $ {{{F}}_{\rm{I}}}{\rm{ = }}{{M}} \cdot {{A}}{\rm{ = }}\left[\!\!\! {\begin{array}{*{20}{c}} {{m_x}}&{}&{} \\ {}&{{m_y}}&{} \\ {}&{}&{{J_{\textit{z}}}} \end{array}}\!\!\! \right]\left[\!\!\! {\begin{array}{*{20}{c}} {{a_x}} \\ {{a_y}} \\ {{a_{M_{\textit{z}}}}} \end{array}}\!\!\! \right] $ | (6) |
图4为试验过程中风洞来流总压和测力天平的输出结果,如图4所示,风洞启动后,总压开始上升,在约650~950 ms保持稳定。试验开始时,气流进入试验段,作用于试验模型上,产生激波,造成测力系统高频振动,因此,首先需对其施加冲击载荷。
 |
| 图4 来流总压及天平测量结果 Fig. 4 Total pressure of the incoming flow and measurement results of the force balance |
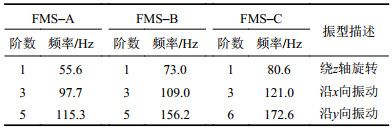
天平各分量输出结果均近似正弦形式,因此确定需要对其施加正弦载荷。为了确定输入载荷的频率,对测力系统进行了模态分析。测力系统模态参数如表2所示,对于FMS–A,轴向、法向和俯仰方向的振动分别为3阶、5阶和1阶模态,对于FMS–B,则分别为3阶、6阶和1阶模态。为了研究天平刚度对输出结果的影响,输入载荷的频率分别为低于FMS–A的固有频率、介于FMS–A、FMS–B和FMS–C的固有频率之间,以及高于FMS–C的固有频率,3种不同频率的载荷分别记为A、B和C,具体描述如表3所示。
| 表2 测力系统模态参数 Tab. 2 Mode parameters of the FMSs |
 |
| 表3 输入载荷参数 Tab. 3 Parameters of the input loads and moment |
 |
4 仿真结果 4.1 冲击载荷加载时测力系统的仿真分析
图5为冲击载荷作用时测力系统的仿真结果。
 |
| 图5 冲击载荷作用时测力系统瞬时仿真结果 Fig. 5 Transient simulation results of the FMS under the action of the step loads and moment |
图5(a)为输入载荷。其中:0~0.02 s输入载荷为0;0.02~0.021 s为加载阶段,推力、升力和俯仰力矩分别从0增加到–2 000 N、3 000 N和1 000 Nm。
图5(b)、(c)和(d)分别为惯性补偿后FMS–A、FMS–B和FMS–C的输出结果。对于FMS–A的弹性输出结果,其中推力、升力和俯仰力矩的输出频率分别为90.2、105.2和50.9 Hz,与其固有频率基本一致,弹性输出结果幅值分别为–3 757.1 N、5 690.3 N和1 759.4 Nm。对于FMS–B的弹性输出结果,其中推力、升力和俯仰力矩的输出频率分别为90.2、137.2和50.9 Hz,弹性输出结果幅值分别为–3 770.27 N、5 631.09 N和1 813.33 Nm。对于FMS–C的弹性输出结果,各分量的输出频率分别为110.6、159.2和74.2 Hz,弹性输出结果幅值分别为–3 817.7 N、5 589.0 N和1 902.1 Nm。
从图5(b)~(d)中可以看出惯性补偿后输出结果的波动消除,输入输出基本一致;FMS–A各分量的幅值分别为–2 051.0 N、3 117.1 N和1 160.7 Nm,FMS–B各分量的幅值分别为–2 048.89 N、3 200.47 N和1 031.32 Nm,FMS–C各分量的幅值分别为–2 083.5 N、3 198.2 N和1 050.6 Nm。
4.2 载荷A加载时测力系统的仿真分析图6为载荷A作用时测力系统的仿真结果。
 |
| 图6 载荷A加载时测力系统瞬时仿真结果 Fig. 6 Transient simulation results of the FMS under the action of load A |
图6(a)为输入载荷。其中,推力、升力和俯仰力矩分别按照表3所描述的规律进行变化,0~0.02为初始阶段,输入载荷为0;0.02~0.17 s为正弦载荷;0.17~0.25 s为结束阶段,载荷为0。
图6(b)、(c)和(d)分别为惯性补偿后FMS–A、FMS–B和FMS–C的输出结果。对于FMS–A的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为5 070.8 N、10 669.2 N和1 894.8 Nm,惯性补偿后各分量的幅值为2 055.5 N、3 031.3 N和1 009.1 Nm。对于FMS–B的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为4 630.8 N、–6 252.9 N和1 695.96 Nm,惯性补偿后各分量的输出结果为2 067.2 N、3 014.1 N和1 097.4 Nm。对于FMS–C的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为3 367.5 N、5 023.6 N和1 642.3 Nm,惯性补偿后各分量的输出结果为2 055.5 N、3 031.3 N和1 023.7 Nm。
从图6中可知,当载荷A施加于测力系统时,FMS–A、FMS–B和FMS–C开始为自由振动和强迫振动的耦合振动,而后为强迫振动;从图6中可以发现,惯性补偿后输入输出曲线基本一致,且幅值较为接近。
4.3 载荷B加载时测力系统的仿真分析图7为载荷B作用时测力系统的仿真结果。图7(a)为输入载荷。其中,推力、升力和俯仰力矩分别按照表3所描述的规律进行变化,0~0.02为初始阶段,输入载荷为0;0.02~0.17 s为正弦载荷;0.17~0.25 s为结束阶段,载荷为0。图7(b)、(c)和(d)为惯性补偿后FMS–A、FMS–B和FMS–C的输出结果。对于FMS–A的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为7 027.8 N、7 918.1 N和2 395.7 Nm,惯性补偿后各分量的输出结果为1 963.8 N、3 059.3 N和1 253.6 Nm。对于FMS–B的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为13 451.2 N、16 190.1 N和–5 547.1 Nm,惯性补偿后各分量的输出结果为2 189.2 N、3 138.0 N和–1 161.1 Nm。对于FMS–C的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为21 350.4 N、22 204.4 N和6 200.67 Nm,惯性补偿后各分量的输出结果为2 239.8 N、3 420.7 N和1 116.5 Nm。
 |
| 图7 载荷B作用时测力系统瞬时仿真结果 Fig. 7 Transient simulation results of the FMS under the action of load B |
从图7中可以看出,加载过程中模型的自由振动被激发;开始时,测力系统为模型自由振动和强迫振动的耦合振动,由于测力系统的加载频率接近相应的固有频率,测力系统的振动明显强于其他情况,尤其是FMS–B。因此,弹性输出载荷和惯性输出载荷较大,惯性补偿后推力、升力和俯仰力矩的输出曲线与输入曲线基本一致。造成两者间少量差异的原因可能是振动过程中,模型产生了一定的弹性变形,导致根据式(6)所得的惯性输出载荷与实际惯性输出载荷存在一定差异,从而造成两者之间的差异。
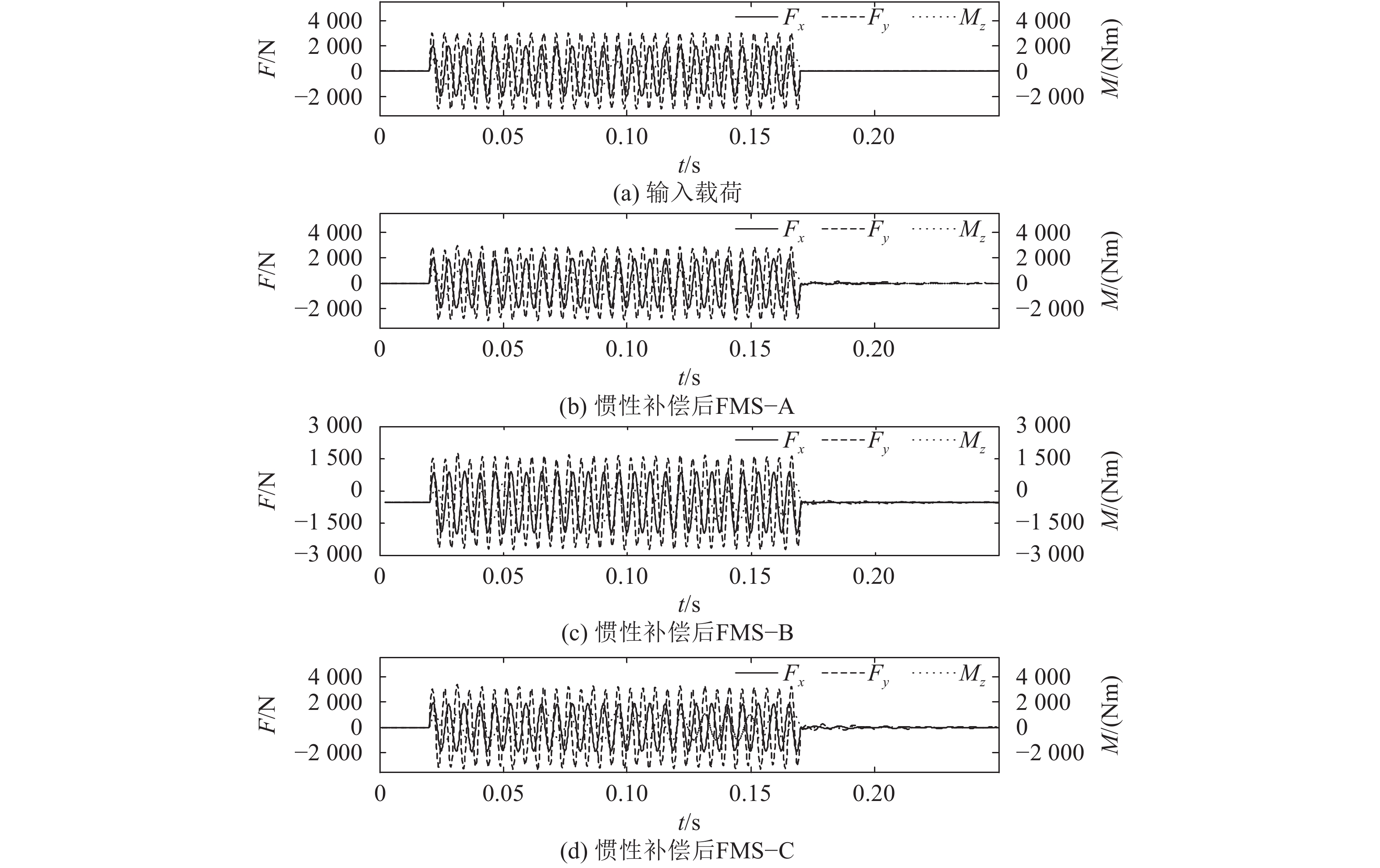
4.4 载荷C加载时测力系统的仿真分析图8为载荷C加载时测力系统的仿真结果。图8(a)为输入载荷。其中,推力、升力和俯仰力矩分别按照表3所描述的规律进行变化,0~0.02为初始阶段,输入载荷为0;0.02~0.17 s为正弦载荷;0.17~0.25 s为结束阶段,载荷为0。
 |
| 图8 载荷C加载时测力系统瞬时仿真结果 Fig. 8 Transient simulation results of the FMS under the action of load C |
图8(b)、(c)和(d)分别为惯性补偿后FMS–A、FMS–B和FMS–C的输出结果。对于FMS–A的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为2 444.9 N、2 916.3 N和799.7 Nm,惯性补偿后各分量的输出结果为1 973.9 N、2 949.9 N和1 181.1 Nm。对于FMS–B的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为–3 015.2 N、5 941.2 N和–1 290.3 Nm,惯性补偿后各分量的输出结果为–2 082.2 N、3 257.9 N和–1 257.2 Nm。对于FMS–C的输出结果,惯性补偿前推力、升力和俯仰力矩弹性输出结果幅值分别为3 846.9 N、9 898.5 N和1 817.3 Nm,惯性补偿后各分量输出结果为1 929.2 N、3 399.9 N和1 108.3 Nm。
从图8中可以看出,加载开始时,测力系统为模型自由振动和强迫振动的耦合;惯性补偿后推力和升力输出曲线与输入曲线基本一致,俯仰力矩输入输出间的固有频率相同,幅值存在一定差异。
5 测量精度分析定义测力系统的测量精度如下:
| $ \alpha = 1 - {{\left| {{E}} \right|} / {{A}}} $ | (9) |
式中,E为测力系统的测量误差,
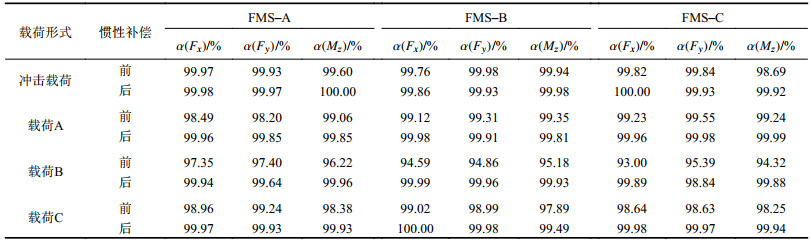
表4为FMS–A、FMS–B和FMS–C各分量的均值测量精度。从表4中可以看出:当冲击载荷加载时,测力系统的均值测量精度普遍高于99.0%,当载荷A和C作用时,测力系统的均值测量精度普遍高于98.0%。当载荷B施加于模型时,测量精度有所下降,特别是FMS–C,其测量精度低于93.0%,然而,惯性补偿后两者的均值测量精度得到了大幅提高,测量精度普遍提高一个数量级,均超过99.6%。对比相同加载时FMS–A、FMS–B和FMS–C惯性补偿前、后的输出结果发现,两者相差较小。该结果证明,弹性输出均值可作为静态气动力测量结果,惯性补偿方法可以进一步提高测力系统的测量精度,但天平刚度对测力系统均值测量结果的影响较小。
| 表4 测力系统均值测量精度 Tab. 4 Mean measurement accuracy of the PBMS |
 |
5.2 瞬时测量精度分析
图9(a)~(d)为FMS–A各分量的测量误差,图10(a)~(d)为FMS–B各分量的测量误差,图11(a)~(d)为FMS–C各分量的测量误差。
 |
| 图9 FMS–A的瞬时测量误差 Fig. 9 Transient measurement errors of FMS–A |
 |
| 图10 FMS–B的瞬时测量误差 Fig. 10 Transient measurement errors of FMS–B |
 |
| 图11 FMS–C的瞬时测量误差 Fig. 11 Transient measurement errors of FMS–C |
由图9可知:对于FMS–A,冲击载荷加载时,推力、升力和俯仰力矩的测量误差范围分别为:–55.00~117.74 N、–179.53~123.28 N和–137.78~139.28 Nm。载荷A加载时,各分量的测量误差范围分别为:–130.980~134.878 N、–338.06~297.20 N和–149.56~158.31 Nm。载荷B加载时,各分量的测量误差范围分别为:–277.07~297.35 N、–562.05~562.94 N和–283.93~310.48 Nm。载荷C加载时,各分量的测量误差范围分别为:–245.58~242.24 N、–585.45~595.89 N和–197.24~186.15 Nm。
由图10可知:对于FMS–B,冲击载荷加载时,推力、升力和俯仰力矩的测量误差范围分别为:–37.3~105.6 N、–147.0~185.9 N和–98.0~98.4 Nm。载荷A加载时,各分量的测量误差范围分别为:–121.7~127.2 N,–252.6~270.0 N和–115.5~98.9 Nm。载荷B加载时,各分量的测量误差范围分别为:–260.9~282.1 N、–328.4~283.0 N和–298.3~301.0 Nm。载荷C加载时,各分量的测量误差范围分别为:–223.5~222.6 N、–495.7~473.1 N和–135.2~153.6 Nm。
由图11可知:对于FMS–C,冲击载荷加载时,推力、升力和俯仰力矩的测量误差范围分别为:–73.53~95.49 N、–155.10~198.20 N和–39.42~60.61 Nm。载荷A加载时,各分量的测量误差范围分别为:–100.58~120.93 N,–145.35~119.01 N和–64.47~60.33 Nm。载荷B加载时,各分量的测量误差范围分别为:–268.20~281.80 N、–293.83~235.35 N和–233.19~253.30 Nm。载荷C加载时,各分量的测量误差范围分别为:–181.50~180.05 N、–328.55~327.05 N和–114.22~115.62 Nm。
表5为测力系统最低测量精度。对于FMS–A,冲击载荷加载时,瞬时测量精度高于87.07%;载荷A加载时,高于84.17%;载荷B加载时,高于68.40%;载荷C加载时,高于80.14%。对于FMS–B,冲击载荷加载时,瞬时测量精度高于90.16%;载荷A加载时,高于90.11%;载荷B加载时,高于69.90%;载荷C加载时,高于83.48%。对于FMS–C,冲击载荷加载时,瞬时测量精度高于93.4%;载荷A加载时,高于93.6%;载荷B加载时,高于85.9%;载荷C加载时,高于88.5%。对比FMS–A、FMS–B和FMS–C的输出结果,可知随着测力天平刚度的提高,测力系统的测量精度逐渐增加。这说明,在一定的范围内,提高测力天平的刚度有助于提高测力系统的瞬时测量精度。
| 表5 测力系统最低测量精度 Tab. 5 Minimum measurement accuracy of FMSs |
 |
6 结 论
采用有限元方法对不同刚度的测力系统进行了仿真分析,并基于惯性补偿方法得到相应的瞬态响应,可以得出以下结论:
1)测力系统的弹性输出结果均值可以作为其静态气动力载荷,但惯性补偿后可以进一步提高测力系统的测量精度,惯性补偿后测量精度高于99.8%。
2)惯性补偿后测力系统的瞬时输出结果可以作为测力系统试验过程中受到的瞬时气动力载荷。
3)天平刚度对测力系统的均值测量精度影响较小,对瞬时测量精度影响较大,在一定范围内,瞬时测量精度随天平刚度的增加而提高。
| [1] |
Tanno H,Komuro T,Sato K,et al. Aerodynamic force measurement technique with accelerometers in the impulsive facility HIEST[J]. Shock Waves, 2009(1): 471-476. DOI:10.1007/978-3-540-85168-4_75 |
| [2] |
Singh P,Menezes V,Irimpan K J,et al. Impulse force balance for ultrashort duration hypersonic test facilities[J]. Shock and Vibration, 2015, 803253. DOI:10.1155/2015/803253 |
| [3] |
Singh P,Trivedi S,Menezes V,et al. Dynamic calibration and validation of an accelerometer force balance for hypersonic lifting models[J]. The Scientific World Journal, 2014(7): 1-8. DOI:10.1155/2014/813759 |
| [4] |
Trivedi S,Menezes V. Measurement of yew,pitch and side-force on a lifting model in a hypersonic shock tunnel[J]. Measurement, 2012, 45: 1755-1764. DOI:10.1016/j.measurement.2012.04.008 |
| [5] |
Robinson M,Hannemann K.Short duration force meas-urements in impulse facilities[C]//Aerodynamic Measurement Technology and Ground Testing Conference.New York:AIAA,2006.
|
| [6] |
Smith A L,Mee D J,Daniel W J,et al. Design,modelling and analysis of a six component force balance for hypervelocity wind tunnel testing[J]. Computers and Structures, 2001, 79(11): 1077-1088. DOI:10.1016/S0045-7949(01)00005-0 |
| [7] |
Collopy A X,Lee S,Marineau E C.Development of dynamic force measurement capabilities at AEDC Tunnel 9[C]//Aerospace Sciences Meeting.New York:AIAA,2014.
|
| [8] |
Wang Y,Liu Y,Luo C,et al. Force measurement using strain-gauge balance in a shock tunnel with long test dura-tion[J]. Review of Scientific Instruments, 2016, 87(5): 1-8. DOI:10.1063/1.4950781 |
| [9] |
He Wei,Tong Zerun,Li Hongbin. Investigation of thrust balance for the single module scramjet[J]. Journal of Aerospace Power, 2010, 25(10): 2285-2289. [贺伟,童泽润,李宏斌. 单模块超燃发动机推力测量天平研制[J]. 航空动力学报, 2010, 25(10): 2285-2289.] |
| [10] |
Lv Jinzhou,Zhang Xiaoqing,Chen Guangxiong,et al. Transient research of force measuring balance to impulse combustion wind tunnel based on inertia compensation[J]. Journal of Vibration and Shock, 2018, 37(2): 216-222. [吕金洲,张小庆,陈光雄,等. 基于惯性补偿的脉冲风洞测力天平瞬态研究[J]. 振动与冲击, 2018, 37(2): 216-222. DOI:10.13465/j.cnki.jvs.2018.02.032] |
| [11] |
Lv Jinzhou,Zhang Xiaoqing,Chen Guangxiong,et al. Transient dynamics research on the force-measurement system for hypersonic impulse combustion wind tunnel based on inertia compensation[J]. Journal of Aerospace Engineering, 2018, 31(6): 04018094. DOI:10.1061/(ASCE)AS.1943-5525.0000914. |
| [12] |
Liu Hongshan,Xu Xiang,Jiang Hua,et al. The application of the stress wave force balance in shock tunnel in China[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(1): 36-39. [刘洪山,徐翔,姜华,等. 应力波天平在国内激波风洞上的应用[J]. 实验流体力学, 2006, 20(1): 36-39. DOI:10.3969/j.issn.1672-9897.2006.01.009] |
 2020, Vol. 52
2020, Vol. 52


