2. 四川大学 水利水电学院 水力学与山区河流开发保护国家重点实验室,四川 成都 610065
2. School of Water Resources & Hydropower, State Key Lab. of Hydraulics and Mountain River Eng., Sichuan Univ., Chengdu 610065, China
根据水电发展“十三五”规划(2016—2020),中国还要兴建一批高坝工程,需采取多种方法开展高坝及其相关水工建筑物的稳定安全研究,其中地质力学模型试验就是重要手段之一[1-4]。
地质力学模型试验的加载方法主要有超载法、降强法、综合法3种。超载法是对上游水荷载按一定的超载频度(ΔP=0.2P~2.0P,P为正常工况下水荷载,下同)逐级进行超载,分级测试坝与地基在各超载阶段的变形和破坏情况。综合法试验也包含超载试验阶段。超载法和综合法共同面临超载频度的取值问题,需要对超载频度经验取值ΔP=0.2P~2.0P的合理性,以及超载频度对模型试验结果的影响问题开展研究。这对地质力学模型能否取得合理试验结果,以及结果的可靠性至关重要。目前一些学者采用不同的超载频度开展了大量的地质力学模型试验研究,如:张泷等[5]采用ΔP=0.5P的超载频度开展大岗山拱坝3维地质力学模型试验;杨宝全、陈媛等[6-7]采用ΔP=0.2P和ΔP=0.3P超载频度对锦屏、立洲拱坝等进行整体稳定性模型试验研究;张强勇等[8]采用间隔侧压系数ΔK=0.5对开挖隧洞进行超载试验;朱维申等[9]采用间隔侧压系数ΔK=1.5对支护后的洞室群进行超载试验;董建华等[10]采用ΔP=0.5P超载频度开展了大岗山双曲拱坝整体稳定3维地质力学模型试验研究;蒋昱州等[11]采用超载频度ΔP=2.0P对伍家岗隧道锚室内3维地质力学模型进行超载;陈建叶等[12]在武都碾压混凝土重力坝深层抗滑稳定模型试验中采用ΔP=0.2P超载频度;周维垣等[13]开展李家峡拱坝地质力学模型试验,前期采用ΔP=0.2P和ΔP=0.3P相互交替,后期采用ΔP=0.5P,前后共加载了36次。目前的试验研究中,超载频度多依据经验取ΔP=0.2P~2.0P,但对超载频度的合理取值及超载频度对试验结果的影响,尚无深入的研究。
本文采用地质力学模型试验法,并结合有限元法和刚体极限平衡法的计算结果,通过分析重力坝典型案例的变位、应变、破坏过程和安全系数等结果,综合评价不同超载频度对大坝试验结果的影响,并确定超载频度的合理取值。并将本研究结果运用于丹巴水电站典型坝段坝基稳定模型试验,评价丹巴水电站典型坝段的坝基稳定性和安全性,揭示薄弱环节,提出加固措施。
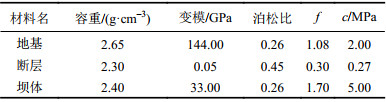
1 重力坝典型案例模型试验 1.1 模型设计与制作为研究地质力学模型试验中超载频度对试验结果的影响,作者以某重力坝19#坝段(坝高102 m)为原型,开展了3个不同超载频度的地质力学模型试验。试验方案对原型大坝的地质条件进行一定的概化,地基中只模拟一条与坝基水平面的夹角为30°断层。概化后更能保证模型加工和试验结果的精度,也便于结果的对比。重力坝地质结构如图1所示,坝体及地质材料参数如表1所示。
 |
| 图1 重力坝典型案例地质结构 Fig. 1 Geological structure of a typical gravity dam |
| 表1 坝体及地质材料参数(原型) Tab. 1 Dam and geological material parameters (prototype) |
 |
考虑3个模型对试验任务、试验精度及试验场地的要求,最终选定模型几何比尺CL=300,原型的模拟范围如下:上游坝基长度81.6 m,坝底长度为70.75 m,下游坝基长度153 m,基础深度为122.4 m,厚度方向模拟30 m,对应模型模拟尺寸为103 cm(顺河向)×40.8 cm(竖直向)×10 cm(横河向)。
模型坝基采用10 cm×10 cm×5 cm的小块体进行砌筑,坝体采用浇筑法整体浇筑,干燥后按照设计尺寸进行精修,最后与坝基进行粘接。
1.2 模型加载与量测模型模拟的荷载包括自重以及上游水压力,自重通过原型、模型材料容重相等来实现,上游水荷载采用油压千斤顶加载。量测系统包括表面变位量测系统和应变量测系统,表面测点布置如图2所示,应变测点主要布置在坝基面。
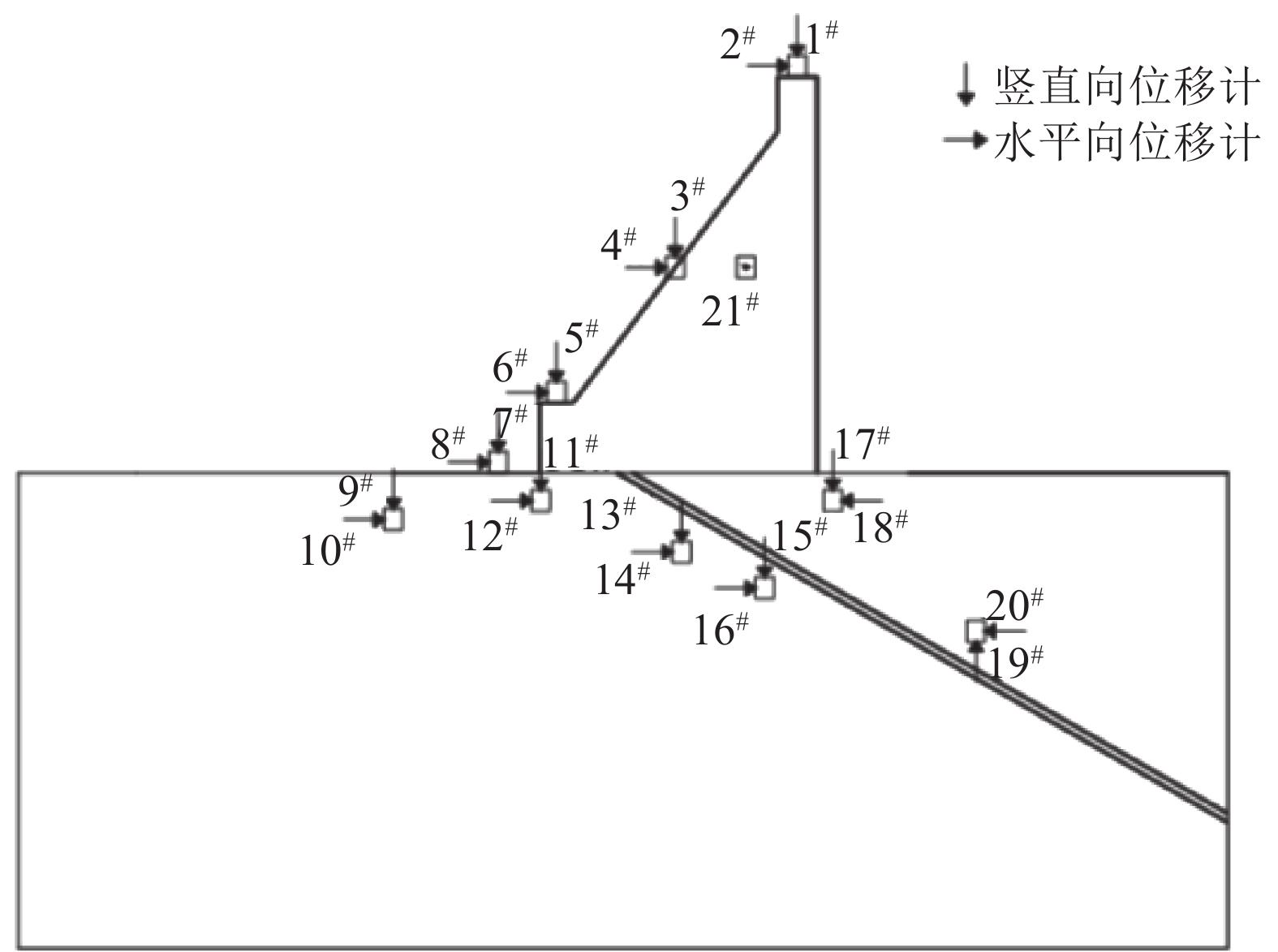 |
| 图2 模型表面变位测点布置 Fig. 2 Arrangement diagram of model surface displacement measuring point |
1.3 不同超载频度试验结果对比
试验时,首先对模型进行预压,消除由于模型砌筑产生的无效变形后缓慢卸荷,而后逐渐加载至正常水荷载1.0P,然后分别按照拟定的0.2P、0.5P和1.0P超载频度逐步加载到模型上(每一个超载频度对应一个模型,共开展3次试验),直至模型出现失稳破坏现象,则停止加载。3次试验分别获得坝与地基变位、坝体应变及模型破坏过程和形态等结果,试验结果的对比如下:
1)坝与地基变位
图3为坝体及坝基部分测点分别在3种不同超载频度下的典型变位关系曲线。由图3可得出:3次试验的结果均表现为坝体总体发生向下游的变位,水平变位大于竖直变位。坝体顶部变位大于下部变位,如2#、4#和6#测点水平变位值随高程降低依次减小;竖直变位在超载前期,坝体以沉降为主,后期以抬升为主。模型整体变位特征符合重力坝的变形规律。
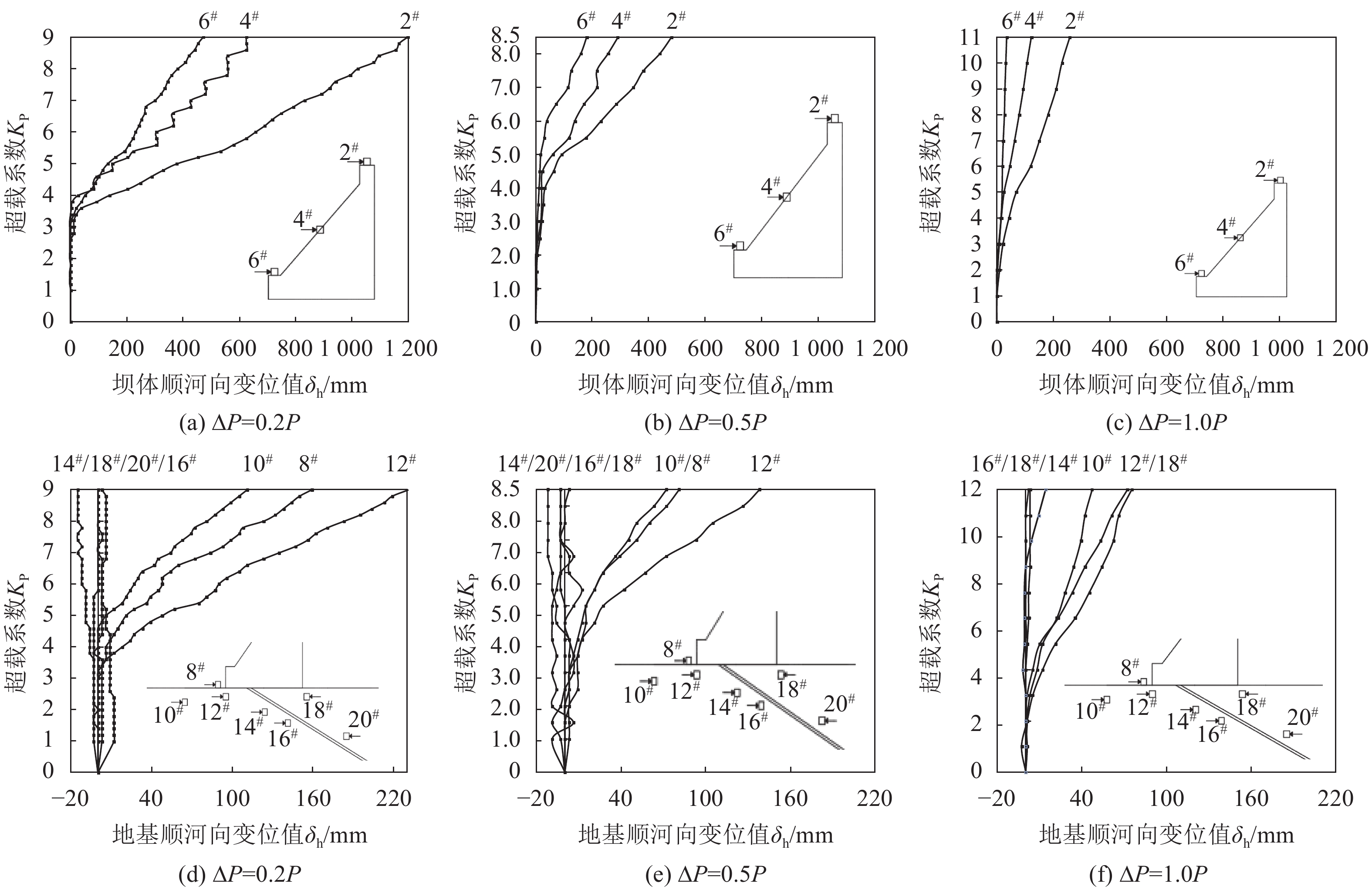 |
| 图3 不同超载频度下坝体及坝基变位关系曲线 Fig. 3 Curves of displacement relationship between dam and dam foundation under different overload frequencies |
对比3次试验结果可知,超载频度越大,其变位关系曲线的拐点越滞后,且同一超载倍数下的测点的变位值越小。如当超载频度ΔP=0.2P时,试验的变位关系曲线在KP=3.8~4.0出现拐点,超载频度为ΔP=0.5P和ΔP=1.0P时,则分别在KP=4.5~5.0和KP=5.0时出现拐点。在数值上,如坝体上4#测点变位值在ΔP=0.2P、0.5P、1.0P超载频度下,KP=2.0时分别为3、0、0 mm,KP=4.0时分别为27、21、15 mm,KP=6.0时分别为306、138、43 mm。
2)坝体应变
图4为不同超载频度下坝体应变测点的应变与超载系数关系曲线。
 |
| 图4 不同超载频度下坝体应变曲线 Fig. 4 Dam strain curves of different overload frequencies |
由图4可得出:ΔP=0.2P超载频度下得到的应变关系曲线表现出明显的拐点;ΔP=0.5P超载频度下的应变关系曲线有波动,但仍有较为明显的拐点;而ΔP=1.0P超载频度得到的应变曲线拐点不太明显。超载频度越大,拐点滞后现象越明显。
3)破坏过程
超载频度对模型破坏过程有影响,同一超载系数下,超载频度小的模型试验破坏范围大。不同超载频度下模型破坏发展中的关键点及其对应的超载系数如表2所示。从表2中可以看出,随着超载频度的增大,模型的破坏过程具有一定的滞后性,如超载频度ΔP=0.2P、0.5P和1.0P模型分别在KP=1.8,KP=2.0,KP=2.0时起裂,ΔP=1.0P的模型裂缝发展相对较滞后。
| 表2 不同超载频度下模型破坏过程 Tab. 2 Model destruction process under different overload frequencies |
 |
4)超载安全系数
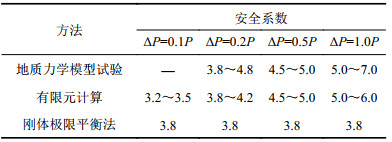
不同超载频度的模型试验得到的超载安全系数有差异。超载频度ΔP=0.2P的模型试验所得到的安全系数为KP=3.8~4.8,超载频度ΔP=0.5P的模型试验所得到的安全系数为KP=4.5~5.0,超载频度ΔP=1.0P的模型试验所得到的安全系数为KP=5.0~7.0。
2 超载频度影响性分析及其合理取值从第1.3节的模型试验结果对比可知,超载频度对模型试验结果有较明显的影响,进一步采用有限元法和刚体极限平衡法,对试验结果进行对比、补充和验证,从而综合分析超载频度的合理取值。
2.1 有限元法运用ANSYS软件,基于本文拟定的重力坝典型案例,建立如图5所示的有限元模型。有限元模型与地质力学模型试验模拟范围一致,见图1,数值计算的材料参数也与模型试验一致,见表1。岩体强度采用Drucker–Prager屈服准则(D–P准则),数学模型离散中坝体采用solid65单元,岩体采用solid45单元。模型共计有限单元总数为4 380个,节点总数为5 784个。计算模型采用的坐标系为:水平方向为X轴方向,以向上游为正;竖直方向为Y轴方向,以向上为正;底面为三向约束,上下游面与前后面采用法向约束。有限元计算加载方案采用4种不同的超载频度,即ΔP为0.1P、0.2P、0.5P、1.0P。
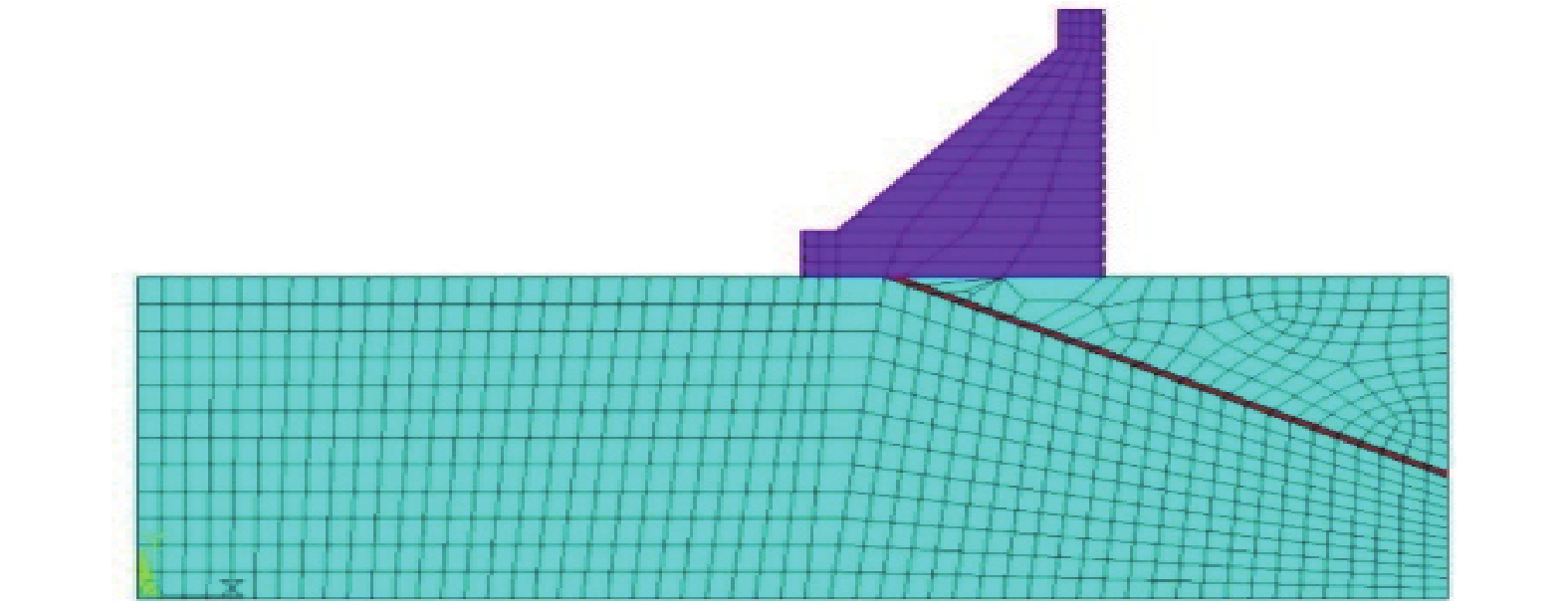 |
| 图5 有限元模型 Fig. 5 Finite element model |
分析有限元计算结果,进一步论证不同的超载频度对变位、破坏形态及安全系数影响。
1)超载频度ΔP对变位的影响
以坝体典型节点变位为例分析,图6为不同超载频度下的典型节点的竖直向变位关系曲线,正值表示向上变位。
 |
| 图6 不同超载频度下的变位曲线 Fig. 6 Displacement curves of different overload frequencies |
由图6可得:ΔP=0.1P超载频度下的变位曲线在KP=3.2~3.5出现拐点;ΔP=0.2P超载频度下的变位关系曲线在KP=3.8~4.2时出现拐点;ΔP=0.5P超载频度下的变位曲线在KP=4.5~5.0出现拐点;ΔP=1.0P超载频度下的变位曲线在KP=5.0~6.0出现拐点,但不明显。由此可见,随着超载频度的增加,变位曲线拐点的出现存在一定滞后性。
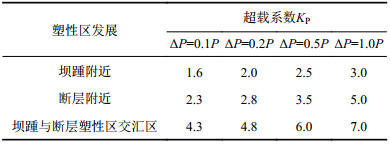
2)超载频度ΔP对塑性区发展的影响
表3列出了不同超载频度下数值模型塑性区发展的关键点及其对应的超载系数。由表3可看出,随着超载频度的增大,模型的塑性区发展表现出一定的滞后,并且在同一超载系数下,超载频度越大,其破坏范围越小,破坏过程有一定的滞后。
| 表3 不同超载频度下模型塑性区发展 Tab. 3 Development of plastic zone of model under different overload frequencies |
 |
3)超载频度ΔP对安全系数的影响
根据不同超载频度下有限元计算得到的坝体、坝基变位及塑性区发展情况,可得到ΔP=0.1P超载频度的安全系数为KSP=3.2~3.5,ΔP=0.2P超载频度的安全系数KSP=3.8~4.2,ΔP=0.5P超载频度的安全系数为KSP=4.5~5.0,ΔP=1.0P超载频度的安全系数为KSP=5.0~6.0。所以,超载频度对数值计算的安全系数有一定的影响,超载频度越大,安全系数越大。
2.2 刚体极限平衡法综合分析模型试验和有限元得到的破坏形态,坝与坝基整体失稳的滑裂面由坝踵至断层的破裂面、沿断层的滑裂面及坝趾底部建基面上的破裂面构成,根据这些破裂面,拟定坝基深层抗滑稳定计算滑裂面,借助MATLAB软件中solve命令,求得坝基抗滑稳定安全系数K=K1=K2=K3=3.8。
2.3 超载频度的影响及合理取值通过以上超载频度的影响性分析,较小的超载频度获得的变位及应变关系曲线阶段性明显,可以较准确地反映出变位及应变的线性阶段、大变形阶段及整体失稳破坏等整个过程,并且较明显的拐点也有利于超载安全系数的判定,获得的坝体应变分布特征也更为精确,但过小的超载频度会增长试验所需时间。
从破坏情况来看,在相同超载系数下,超载频度越小,破坏范围较大,越有利于观测破坏形态及揭示坝基薄弱部位。
3种方法得到的安全系数如表4所示。从安全系数上看,超载频度越大,其安全系数越大,对于工程则偏危险。同时,安全系数K的确定可参考工程中应用较多推荐的刚体极限平衡法的计算结果,ΔP=0.2P超载频度得到的超载安全系数与刚体极限平衡法计算得到的安全系数较为一致。
| 表4 各种方法得到的安全系数 Tab. 4 Safety factors obtained by various methods |
 |
综上,从超载频度对试验结果各方面的影响考虑,结合工程的安全性、试验操作的可行性等要求,在大坝与地基整体稳定地质力学模型超载法中选取超载频度ΔP=0.2P比较合理、可行。
3 丹巴水电站典型坝段稳定性研究 3.1 工程概况丹巴水电站是大渡河水电站规划的第8级电站,位于四川省甘孜藏族自治州丹巴县境内,其闸坝坝高42 m,坝基覆盖层深厚,最大厚度达127.66 m,结构及组成复杂,坝基覆盖层自上而下总共分为5层,其变形模量较低,压缩性大,坝基稳定性问题突出。
3.2 坝基稳定试验研究针对丹巴水电站坝与地基整体稳定性问题,开展地质力学模型试验。模型几何比CL=100,模型的模拟范围尺寸为:1.73 m×0.23 m×1.08 m(纵向×横向×高度),相当于原型工程173 m×23 m×108 m范围。试验中分别研制了各覆盖层的相似模型材料,并按照各覆盖层分布采用分层夯实法进行模型砌筑,最后在坝基上粘接重力坝坝体,模型砌筑完成全貌如图7所示。采用超载法分析坝体在超载作用下,坝体、覆盖层和上游防渗墙变位分布特征、破坏过程及破坏形态,并得到超载安全系数,其中超载频度为论证得到的较为合理的超载频度,即ΔP=0.2P。
 |
| 图7 模型砌筑完成全貌 Fig. 7 Whole picture of the completed model |
1)坝体变位分布特征
坝体顺河向变位方向总体向下游,坝顶变位最大;在正常蓄水位工况下,2#点的顺河向变位为6.4 cm(原型值),顺河向变位随高程降低逐渐减小,符合常规。坝体典型变位曲线如图8所示。由坝体顺河向变位关系曲线可知:KP小于1.6时,变位关系曲线呈线性发展;当KP为1.6~2.0时,变位关系曲线出现较为明显的拐点;随着超载倍数的增加,变位关系曲线逐步增长,直至数据出现不稳定,试验结束。
 |
| 图8 坝体顺河向变位关系曲线 Fig. 8 Displacement curves of the dam body along the river |
2)下游覆盖层表面变位分布特征
下游覆盖层典型表面变位曲线如图9所示。由下游覆盖层表面顺河向变位关系曲线可知:当KP小于1.6时,各测点变位曲线基本呈线性发展;当KP为1.6~2.0时,多数变位曲线出现较为明显的拐点;随着超载倍数的增加,变位关系曲线逐步增长,直至数据出现不稳定,试验结束。
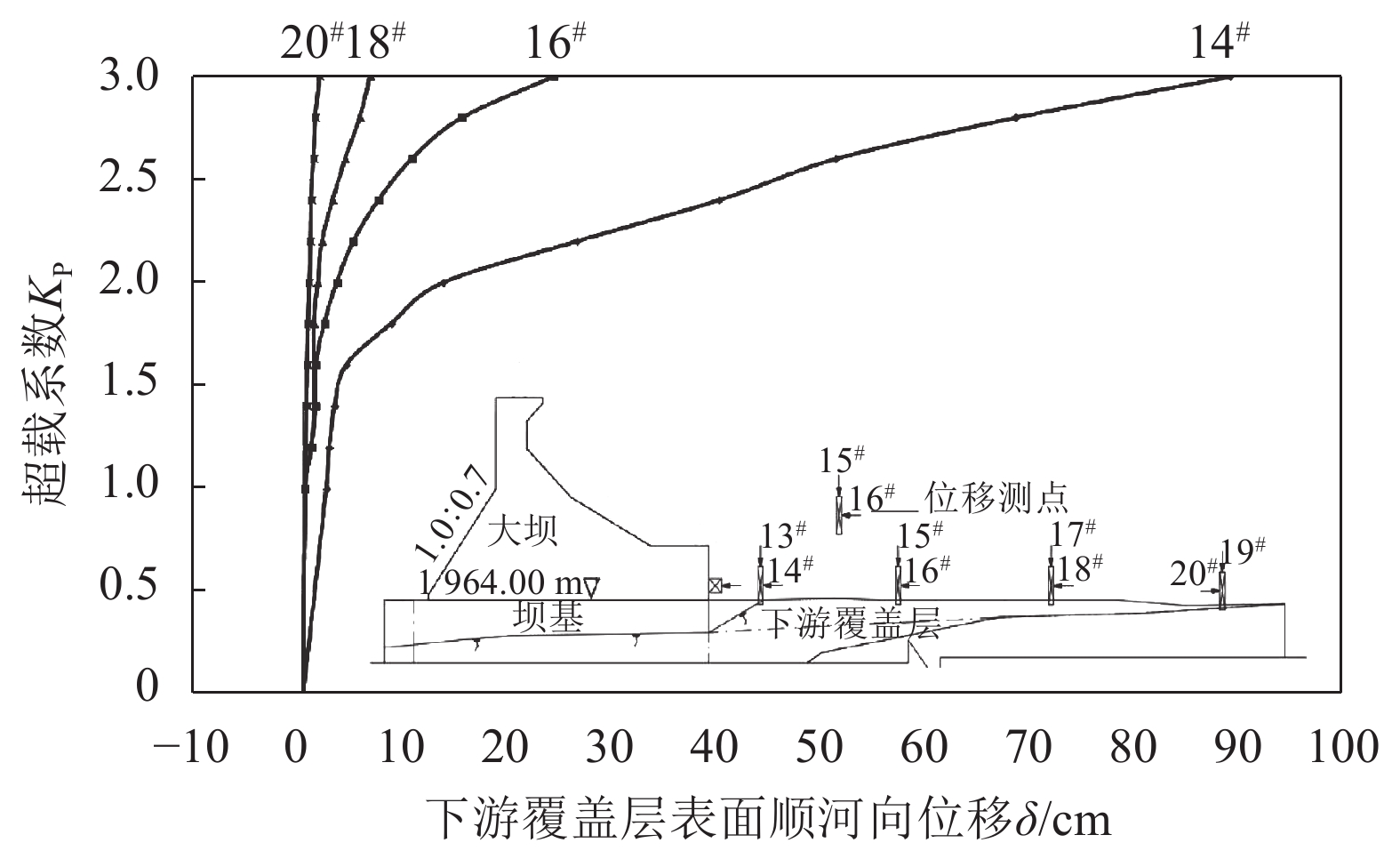 |
| 图9 下游覆盖层表面顺河向变位关系曲线 Fig. 9 Curves of the downstream displacement of the downstream cover layer surface |
3)破坏过程及破坏形态
模型的整个破坏过程为:KP=1.0时,坝与地基整体工作性态正常,产生较小的表面变位值及接触面的相对变位值,未发生开裂;随着超载倍数的增加,变位值逐渐增大,但模型未开裂,当KP=1.6时,坝踵附近的基础覆盖层回填料(天然区)出现微裂纹;超载至KP=1.8~2.0时,基础覆盖层回填料(天然区)裂纹逐渐扩展,回填料(固结灌浆区)出现微裂纹。超载至KP=2.0~2.4时,建基面严重开裂,下游基础覆盖层部分隆起,形成裂缝。
图10给出了模型的最终破坏形态。由图10可知:模型破坏区域主要出现在坝体与基础接触部位上,建基面严重开裂,下游基础覆盖层部分隆起,形成裂缝;坝趾下游的回填料(天然区)与坝基回填料(固结灌浆区)之间出现贯穿裂缝。模型的破坏过程和破坏机理表现为重力坝沿建基面的失稳破坏模式,即先在坝踵处产生拉剪破坏,坝趾处产生压缩破坏,然后逐渐沿建基面形成贯通性裂缝,最后形成失稳趋势。
 |
| 图10 模型破坏形态 Fig. 10 Model damage form |
4)超载安全系数评价
综合模型中各测点变位关系曲线和应变关系曲线的波动、拐点、增长速度、转向等特征,并结合模型的破坏过程等结果,可知:超载至1.4P时发生初裂;超载到1.6P~2.0P时,变位关系曲线和应变关系曲线出现明显的转折和拐点,建基面基础与坝体接触部位出现裂缝,发生大变形,故可得到典型坝段超载安全系数为KSP=1.6~2.0,由于地质力学模型试验安全系数当前尚无明确的评判水准,参考《水闸设计规范》,所得的安全系数比规范允许值大(K ≥1.3),说明闸坝与地基是稳定的。
3.3 坝基稳定评价通过对丹巴水电站典型坝段进行模型试验,获取了坝与地基的变位分布特征、变位关系曲线,以及破坏过程、破坏形态,得到其整体稳定超载安全系数KSP=1.6~2.0,大于《水闸设计规范》要求,但总体上是稳定的。对坝基开裂破坏较早的薄弱部位,建议下阶段采取设置抗滑桩、水泥灌浆等多种工程措施,以提高坝基抗滑能力。
4 结论与展望1)通过典型重力坝的3个不同超载频度地质力学模型试验结果对比可知,超载频度ΔP对地质力学模型试验结果存在一定的影响:超载频度越大,测点变位的量值越小,变位关系曲线出现的拐点越滞后;较小的超载频度可以得到较为准确的坝体应变分布规律,其应变曲线有较明显的拐点;随着超载频度的增大,破坏过程有一定滞后,同一超载系数KP下,超载频度越大,模型破坏范围越小;随着超载频度越大,结构的超载安全系数越大。研究结果为大坝稳定地质力学模型试验的加载方式提供科学依据,并有助于提高试验结果的可靠性。
2)结合典型重力坝稳定分析模型试验与有限元计算结果,并参考刚体极限平衡法结果,分别从变位、应变、破坏情况和安全系数等方面进行综合分析,根据试验操作的可行性、变位发展的充分性、工程的安全性、安全系数精度等方面的要求,超载频度取值为ΔP=0.2P较为合理。
3)将分析得到的合理超载频度运用到丹巴水电站典型坝段坝与地基整体稳定研究中,得到丹巴水电站典型坝段地质力学模型超载安全系数为KSP=1.6~2.0,总体满足规范要求。评价了丹巴水电站典型坝段的坝基稳定性和安全性,为该工程的设计和施工提供参考。
4)超载频度对坝与地基超载法模型试验及数值计算结果均有影响,下阶段可进一步展开对不同坝型、坝基等超载频度ΔP的取值研究。
| [1] |
Zhang Chuhan. Crucial techniques high dams and hydroPower projects[J]. Journal of China Three Gorges University (Natural Sciences), 2004, 26(3): 193-197. [张楚汉. 高坝–水电站工程中的关键科学问题[J]. 三峡大学学报(自然科学版), 2004, 26(3): 193-197.] |
| [2] |
Shen Tai. Development of geomechanic model experiment techniques[J]. Journal of Yangtze River Scientific Research Institute, 2001, 18(5): 32-35. [沈泰. 地质力学模型试验技术的进展[J]. 长江科学院院报, 2001, 18(5): 32-35. DOI:10.3969/j.issn.1001-5485.2001.05.008] |
| [3] |
Yang Baoquan,Xiong Ke,Chen Yuan,et al. Deformation monitoring information of geo-mechanical model test and its application in engineering[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(4): 17-24. [杨宝全,熊科,陈媛,等. 地质力学模型试验中的变位信息监测及其在工程中的应用[J]. 四川大学学报(工程科学版), 2015, 47(4): 17-24.] |
| [4] |
Dong Jianhua,Zhang Lin,Xu Yuanfei,et al. Application of catastrophe theory to determine the instability criterion for geo-mechanical model test[J]. Advanced Engineering Sciences, 2017, 49(4): 18-25. [董建华,张林,徐远飞,等. 突变理论在地质力学模型试验失稳判据中的应用[J]. 工程科学与技术, 2017, 49(4): 18-25.] |
| [5] |
Zhang Long,Liu Yaoru,Yang Qiang,et al. Geomechanical model test on global stability of a arch dam at Dagangshan[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 971-982. [张泷,刘耀儒,杨强,等. 基于地质力学模型试验的大岗山拱坝整体稳定性分析[J]. 岩石力学与工程学报, 2014, 33(5): 971-982.] |
| [6] |
Yang Baoquan,Zhang Lin,Chen Yuan,et al. Experimental and numerical comprehensive analysis on overall stability of Jinping Ⅰ high arch dam[J]. Journal of Hydraulic Engineering, 2017, 48(2): 175-183. [杨宝全,张林,陈媛,等. 锦屏一级高拱坝整体稳定物理与数值模拟综合分析[J]. 水利学报, 2017, 48(2): 175-183.] |
| [7] |
Chen Yuan,Zhang Lin,Yang Baoquan,et al. Geomechanical model experiment of global stability of Lizhou arch dam on Muli River[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Supp2): 3928-3935. [陈媛,张林,杨宝全,等. 木里河立洲拱坝整体稳定地质力学模型试验研究[J]. 岩石力学与工程学报, 2012, 31(增刊2): 3928-3935.] |
| [8] |
Zhang Qiangyong,Li Shucai,Li Yong,et al. 3D geomechanical model test research on stability and supporting for surrounding rock mass of a large-scale diversion tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp2): 4051-4059. [张强勇,李术才,李勇,等. 大型分岔隧道围岩稳定与支护三维地质力学模型试验研究[J]. 岩石力学与工程学报, 2007, 26(增刊2): 4051-4059.] |
| [9] |
Zhu Weishen,Li Yong,Zhang Lei,et al. Geomechanical model test on stability of cavern group under high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1308-1314. [朱维申,李勇,张磊,等. 高地应力条件下洞群稳定性的地质力学模型试验研究[J]. 岩石力学与工程学报, 2008, 27(7): 1308-1314. DOI:10.3321/j.issn:1000-6915.2008.07.002] |
| [10] |
Dong Jianhua,Xie Heping,Zhang Lin,et al. Experimental study of 3D geomechanical model on global stability of Dagangshan double curvature arch dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2027-2033. [董建华,谢和平,张林,等. 大岗山双曲拱坝整体稳定三维地质力学模型试验研究[J]. 岩石力学与工程学报, 2007, 26(10): 2027-2033. DOI:10.3321/j.issn:1000-6915.2007.10.010] |
| [11] |
Jiang Yuzhou,Wang Ruihong,Zhu Jiebing,et al. Geomechanical model test on global stability for Wujiagang bridge tunnel-type anchorages[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Supp2): 4103-4113. [蒋昱州,王瑞红,朱杰兵,等. 伍家岗大桥隧道锚三维地质力学模型试验研究[J]. 岩石力学与工程学报, 2016, 35(增刊2): 4103-4113.] |
| [12] |
Chen Jianye,Zhang Lin,Chen Yuan,et al. Failure model test on deep anti-sliding stability of Wudu RCC gravity dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2097-2103. [陈建叶,张林,陈媛,等. 武都碾压混凝土重力坝深层抗滑稳定破坏试验研究[J]. 岩石力学与工程学报, 2007, 26(10): 2097-2103. DOI:10.3321/j.issn:1000-6915.2007.10.020] |
| [13] |
周维垣,林鹏,杨若琼.高拱坝地质力学模型试验方法与应用[M].北京:中国水利水电出版社,2008.
|
 2020, Vol. 52
2020, Vol. 52


