为了保证在发射过程中音频信号不被篡改或污染,需要对发射前的音频信号和发射信号的接收解调结果进行比对[1]。目前广播节目监播这一工作大多是人工完成的[2],即广播监播机接收广播信号并解调,监测人员循环播放和监听辨别。广播发射台常有多路广播节目信号需要发射,所以人工音频监播的工作量很大,无法达到实时监播的要求。并且,同一套广播节目的音频信号一般都是由不同传输链路(卫星、光纤、微波、网络)传输的,各路信号到达各节点会存在时间延迟[3]。当两音频不同步时,音频比对不能得到准确的相似度[4]。因此,在音频比对之前需要先估计出两音频信号间的延时,并将两音频同步,同步结果对音频比对结果(即相似度)的准确度影响很大[5]。
通常,传统的音频相似度计算方法主要有两步[6]:先提取音频的特征参数[7],如音频信号的包络、短时能量、基因频率、梅尔频率倒谱系数(MFCC)[8]、线性预测倒谱系数(LPCC)[9]等特征;再使用距离测量等方法比较这些特征参数的差异,从而得出两路音频的相似度[10]。传统方法只能针对普通音频,不适用于广播音频,其原因主要有3个方面:一是,如果两路实时广播音频之间存在延时,用音频特征参数计算所得到的音频相似度结果就不准确。二是,在容错性方面,文献[11]中指出众多音频特征参数都是以准确描述音频为目标,音频的细微变化都会反映在音频特征参数上,从而达到比较高的音频内容辨识度。如果所输入的两个相同音频含有噪声干扰,或是经过一些不同通带的滤波器(如带通滤波器)处理,会使两音频之间有较大的差异[12],故用音频特征参数计算相似度时通常会误判为两音频相似度很低甚至完全不同。而广播音频在制作时需要进行滤波处理,在传输过程中会存在噪声干扰。在广播音频监测中,需要比对卫星接收机的音频和广播监播机接收到的音频,前者一般是没有任何噪声的,后者常常含有噪声干扰。针对广播音频比对,主要在于判断两音频的内容是否相同,而不在于听觉效果上是否完全一致,所以对于受到噪声干扰和经过滤波器处理的广播音频,传统方法会误判两音频相似度较低。三是,在相似度的计算效率方面,提取音频特征参数以计算两实时音频的相似度的传统方法计算复杂度相对较高[13],高性能的计算机和较长的计算时间,因此传统方法不适合用于广播音频实时比对。目前,也有不用提取音频特征参数进行音频比对的方法,如文献[14]中将需要比对的两音频归一化后分为低频带、中频带和高频带,相同频带的音频短时能量求和后做减法,选取合适阈值判断减法结果从而得到音频相似度。由于该算法在时域中处理,因此计算简单并且只需要较短的计算时间,但是该方法同样只能用于比对没有时间延迟的两音频。
针对以上问题,本文提出一种基于倒谱分析的实时音频相似度快速比对算法。若两音频存在延时,该算法不需要先将两音频同步,可直接对两音频进行延时估计和音频比对,算法抗噪声性能较强,计算时间短,可得到较准确的延时估计结果和音频比对结果。
1 传统计算相似度的方法要确定两样本之间的相似性,可采用不同的方法。一般而言,传统的音频相似度测量可以分为两类。一是,基于距离,如Minkowski距离、Mahalanobis距离和Canberra距离。这些方法将提取到的音频特征向量,如音频的MFCC特征向量,视为度量空间中的点,点与点之间的距离越大,相似性越小,反之亦然。二是,基于相关系数,例如,余弦相似度和Pearson相关系数。所得相似度范围为–1到1,1表示完全相同,–1表示完全不同,0通常表示独立性,中间值表示一定程度的相似或不相似。表1中描述了典型的相似度测量方法,其中,
| 表1 典型的相似度测量方法 Tab. 1 Typical methods of similarity measures |
 |
Minkowski距离通常取
倒谱(cepstrum)是对信号频谱的对数进行傅里叶反变换(IFT)的结果。倒谱有复数倒谱、实数倒谱、功率倒谱和相位倒谱。功率倒谱在人类语言分析中有着特殊的应用。本文倒谱分析用的是功率倒谱。倒谱可以看作是关于不同谱带的变化率的信息,它最初是用于描述地震和炸弹爆炸引起的地震回声。该方法对功率谱中的等距频率分量具有较强的分辨率,能够有效地识别信号中的回波分量。若给定时间信号
| $ Y(\omega ) = {{\cal F}}[y(t)] = \int\limits_{ - \infty }^{ + \infty } {y(t){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} $ | (1) |
其功率谱为:
| $ {S\!_{{y}}}(\omega ) = {\left| {Y(\omega )} \right|^2} = {\left| {{\cal F}}[y(t)] \right|^2} $ | (2) |
其功率倒谱为:
| $ {C_{{y}}}\left( \tau \right) = {{\cal F}}^{ - 1}\left[ {\ln {S\!_{{y}}}\left( \omega \right)} \right] = \displaystyle\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{2\text{π}}}\left[ {\ln {S\!_{{y}}}\left( \omega \right)} \right]{{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega } $ | (3) |
信号自相关函数与其功率谱函数也是一对傅里叶变换:
| $ {R_{{y}}}\left( \tau \right) = {{\cal F}}^{ - 1}\left( {{S\!_{{y}}}\left( \omega \right)} \right) = \displaystyle \int\limits_{ - \infty }^{ + \infty } {\frac{{\rm{1}}}{{{\rm{2\text{π} }}}}{S\!_{{y}}}(\omega ){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega } $ | (4) |
两者对比可见,功率倒谱与自相关函数具有相同的量纲,即具有一致的物理意义。回声是源信号与其延迟信号相叠加得到的,因为源信号与延迟信号具有强相关性,所以从含有延迟信号的混合信号的自相关函数上看,在时间延迟量位置上会具有较高峰值。信号间时域卷积对应其频域的乘积,功率倒谱把时域卷积的复杂关系转化成为时延域的简单相加关系,因此,在信号功率倒谱的同样位置也将出现高峰值,且更为明显。
2.2 倒谱分析法计算音频相似度的原理假设
| $ \left\{\!\!\!\! {\begin{array}{*{20}{l}} {{x_1}(t) = {a_1}x(t),}\\ {{x_2}(t) = {a_2}x(t - {\tau _0})} \end{array}} \right. $ | (5) |
式中:
构造混合信号为:
| $ \begin{aligned}[b] y(t) = &{x_1}(t) + {x_2}(t) = {a_1}x(t) + {a_2}x(t - {\tau _0}) = \\ &x{(t)^{\rm{*}}}({a_1}\delta (t) + {a_2}\delta (t - {\tau _0})) \\ \end{aligned} $ | (6) |
式中,
| $ Y(\omega ) = X(\omega )({a_1} + {a_2}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}}) $ | (7) |
对于式(7),其功率谱密度函数为:
| $\begin{aligned}[b] {S\!_{{y}}}(\omega ) =& {\left| {Y\left( \omega \right)} \right|^2} = Y\left( \omega \right){Y^{\rm{*}}}\left( \omega \right) = \\ &X\left( \omega \right)\left( {{a_1} + {a_2}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}}} \right) \cdot {X^{\rm{*}}}\left( \omega \right){\left( {{a_1} + {a_2}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}}} \right)^{\rm{*}}} = \\ &{S\!_{{x}}}\left( \omega \right)\left( {{a_1} + {a_2}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}}} \right) \cdot \left( {{a_1} + {a_{2}}{{\rm{e}}^{{\rm{j}}\omega {\tau _0}}}} \right) \end{aligned} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (8) |
式中,上标“*”表示复共轭运算。式(8)由3个乘积项构成。为分离这3项,对式(8)两边取对数,得:
| $ \ln \left[ {{S\!_{{y}}}(\omega )} \right] = \ln \left[ {{S\!_{{x}}}\left( \omega \right)} \right] + \ln \left( {{a_1} + {a_2}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}}} \right) + \ln \left( {{a_1} + {a_2}{{\rm{e}}^{{\rm{j}}\omega {\tau _0}}}} \right) $ | (9) |
利用对数函数的级数展开式:
| $ \begin{aligned}[b] \ln (a + x) =& \ln a + \dfrac{x}{a} - \dfrac{{{x^2}}}{{2{a^2}}} + \frac{{{x^3}}}{{3{a^3}}} - \cdots = \\ &\ln a + \sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\dfrac{{{x^n}}}{{n{a^n}}}} \end{aligned} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (10) |
取式(10)前两项做近似,式(9)可写为:
| $ \begin{aligned}[b] \ln {S\!_{{y}}}(\omega ) =& \ln {S\!_{{x}}}\left( \omega \right) + \ln {a_1} + \dfrac{{{a_2}}}{{{a_1}}}{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}} - \dfrac{{{a_2}^2{{\rm{e}}^{ - {\rm{j}}2\omega {\tau _0}}}}}{{2{a_1}^2}} + \\ & \ln {a_1} + \dfrac{{{a_2}}}{{{a_1}}}{{\rm{e}}^{{\rm{j}}\omega {\tau _0}}} - \dfrac{{{a_2}^2{{\rm{e}}^{{\rm{j}}2\omega {\tau _0}}}}}{{2{a_1}^2}} \end{aligned} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (11) |
对式(11)两边取傅里叶变换,将时域变量记为
| $ \begin{aligned}[b] &{{\cal F}^{ - 1}}\left\{ {\ln {S\!_{{y}}}(\omega )} \right\} = {{\cal F}^{ - 1}}\left\{ {\ln {S\!_{{x}}}\left( \omega \right)} \right\} + \dfrac{{{a_2}}}{{{a_1}}}\delta \left( {\tau - {\tau _0}} \right) - \\ &\;\;\;\;\dfrac{{{a_2}^2}}{{2a_1^2}}\delta \left( {\tau - 2{\tau _0}} \right) + \dfrac{{{a_2}}}{{{a_1}}}\delta \left( {\tau + {\tau _0}} \right) - \dfrac{{{a_2}^2}}{{2a_1^2}}\delta \left( {\tau + 2{\tau _0}} \right) + 2\ln {a_1} \end{aligned} $ | (12) |
依据功率倒谱定义,将式(12)简化为:
| $ \begin{aligned}[b] {C_{{y}}}\left( \tau \right) \!=& {C_{{x}}}\left( \tau \right) \!+\! \dfrac{{{a_2}}}{{{a_1}}}\delta \left( {\tau \!-\! {\tau _0}} \right) - \dfrac{{{a_2}^2}}{{2a_1^2}}\delta \left( {\tau - 2{\tau _0}} \right) + \\ & \dfrac{{{a_2}}}{{{a_1}}}\delta \left( {\tau + {\tau _0}} \right) - \dfrac{{{a_2}^2}}{{2a_1^2}}\delta \left( {\tau + 2{\tau _0}} \right) + 2\ln {\rm{ }}{a_1} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \end{aligned} $ | (13) |
由式(13)可以看出,混合信号的功率倒谱中,在时间延迟位置及其整数倍位置上有冲激峰量。由此,只要检测出冲激峰量,即可根据其位置得出两路音频信号之间的延迟
图1为倒谱分析计算音频相似度的流程图。输入为两路音频信号,分别称为卫星音频
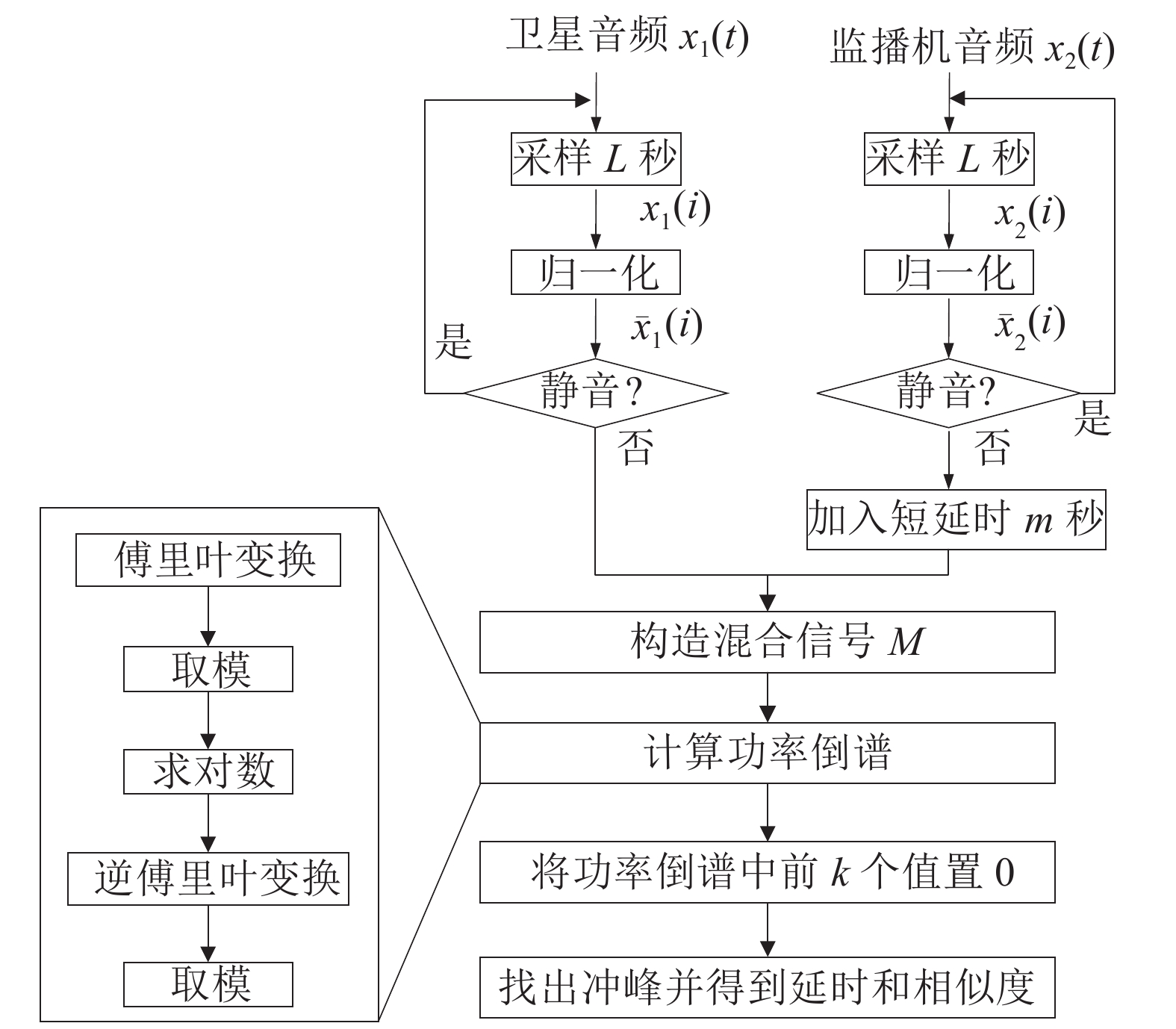 |
| 图1 基于功率倒谱的音频相似度计算方法 Fig. 1 Audio similarity calculation method based on power cepstrum |
使用式(14)归一化采样数据
| $ \bar x(i) = \frac{{x(i)}}{{\sqrt {\displaystyle\sum\limits_{i = 0}^N {{{[x(i)]}^2}} } }} $ | (14) |
式中,
| ${X_{\rm{s}}} = \sum\limits_{i = 0}^N {\left| {\bar x(i)} \right|} $ | (15) |
若
再按照式(16)将两信号叠加合并得到混合信号
| $ M = \frac{{{{\bar x}_1}({i_1}) + {{\bar x}_2}({i_2} - m \cdot {f_{\rm{s}}})}}{2} $ | (16) |
式中:
对信号
| $ {\tau _0} = \frac{{{p_{\rm{s}}} - m \cdot {f_{\rm{s}}}}}{{{f_{\rm{s}}}}} $ | (17) |
根据课题组的其他实验研究可知,冲激峰量的幅度范围为0~0.45。当完全一样的两音频作为输入时,冲激峰量的幅度为0.45;当完全不一样的两音频作为输入时,冲激峰量的幅度在0.02以下。所以,将0.02作为阈值,冲激峰量幅度大于0.02则认为两音频可能相似,小于0.02则认为不相似。
借鉴PCM编码中的
| $ F(x) ={\rm{sgn}}(x)\frac{{\ln (1 + \mu |x|)}}{{\ln (1 + \mu )}} $ | (18) |
式中,
提出了由功率倒谱中冲激峰幅度计算相似度百分比的公式,将冲激峰幅度映射为相似度百分比:
| $ S = \frac{{\ln (0.15 + 50\;{\rm{ }}000 \cdot {p_{\rm{a}}})}}{{\ln (0.15 + 50\;{\rm{ }}000)}} \times 100{\rm{\% }} $ | (19) |
为了深入了解所提出的倒谱分析法在无噪声和不同信噪比加性白噪声条件下的性能,进行了以下7个实验。实验的环境平台均为MATLAB R2019a,电脑CPU为i5–3337u,系统为Windows10教育版。
3.1 短延时m的最优选择为探究算法中所加入的短延时
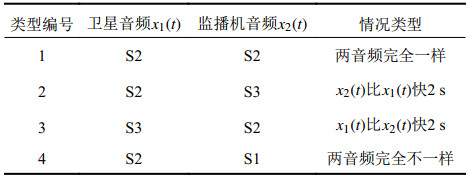
由于传输链路的影响,监播机音频一般都是延后于卫星音频,而备用卫星音频一般延后于监播机音频2到3 s。因此实验中,准备了3个广播电台的音频片段,每个音频片段30 s。其中,音频片段S1和S2内容完全不一样,S2与S3内容是一样的,并且S3比S2快2 s。按照表2将这3个音频片段进行两两组合,模拟了真实环境下卫星音频和监播机音频的4种情况。
| 表2 卫星音频和监播机音频的4种情况 Tab. 2 Four cases of satellite audio and monitor audio |
 |
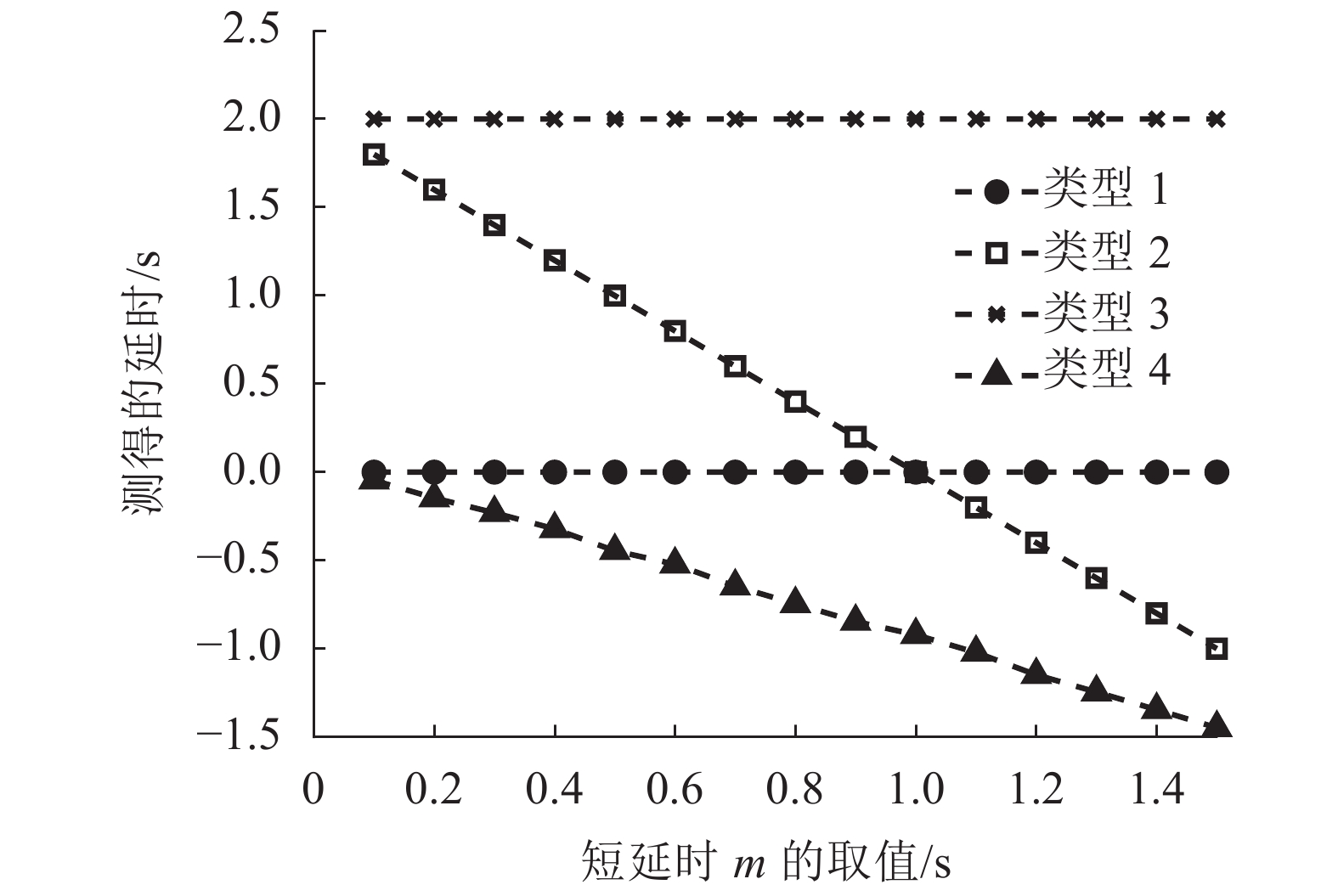
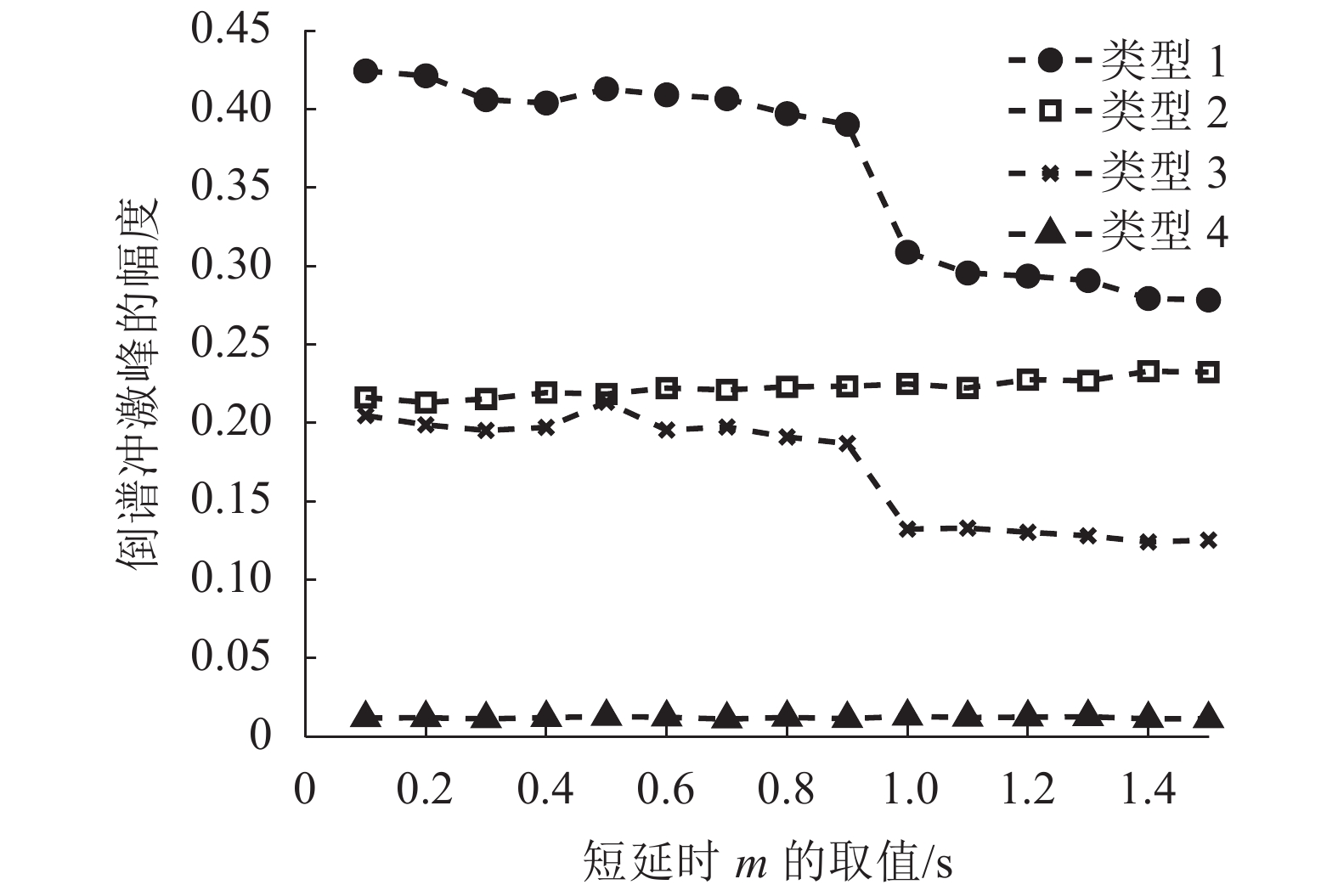
4种情况所测得的两音频间的延时和倒谱冲激峰幅度的变化如图2和3所示。
 |
|
图2 短延时
|
 |
|
图3 短延时
|
从图2可以看出,在类型1和类型3下,所测得的两音频之间的延时不会因加入的短延时
为比较倒谱分析法、基于MFCC的欧氏距离法(简称欧式距离法)这两种音频比对算法在不同信噪比下无延时两音频比对结果,准备了广播电台的50个音频片段作为模版库,每个片段持续10 s,包括音乐,3种不同语种的语音以及音乐和语音的混合音频。对于这些音频片段,加入加性高斯白噪声后获得不同信噪比的音频片段。从中选择了第23个音频作为测试样本。
3.2.1 比对未经过带通滤波器处理的两音频通过倒谱分析法和欧氏距离法分别计算了测试样本与模版库中50个无噪声音频片段之间的相似度。归一化的欧式距离和相似度结果如图4和5所示。欧氏距离越小,代表相似度越大。
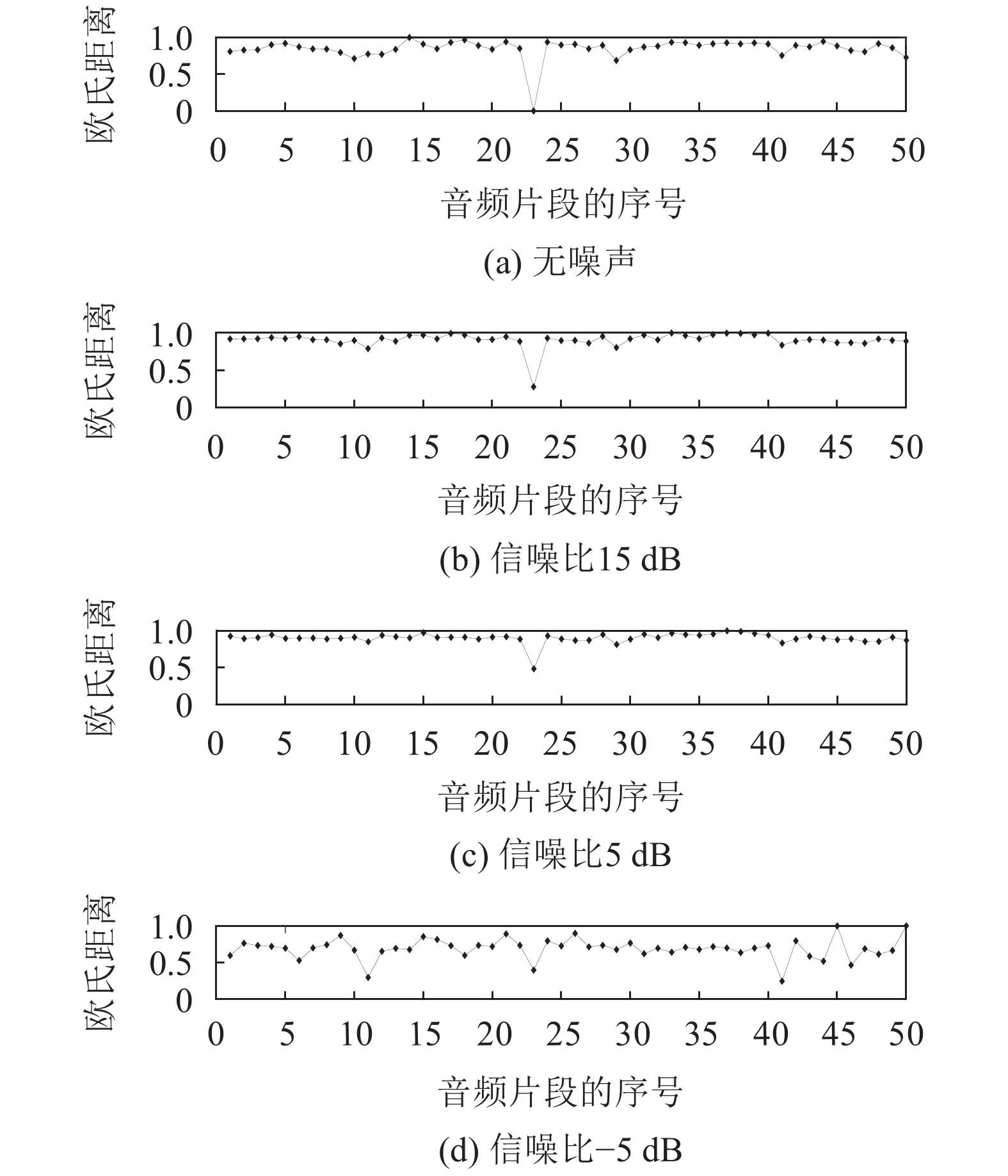 |
| 图4 基于MFCC特征的欧式距离法所测出的欧氏距离 Fig. 4 Measured Euclidean distance by Euclidean distance method based on MFCC features |
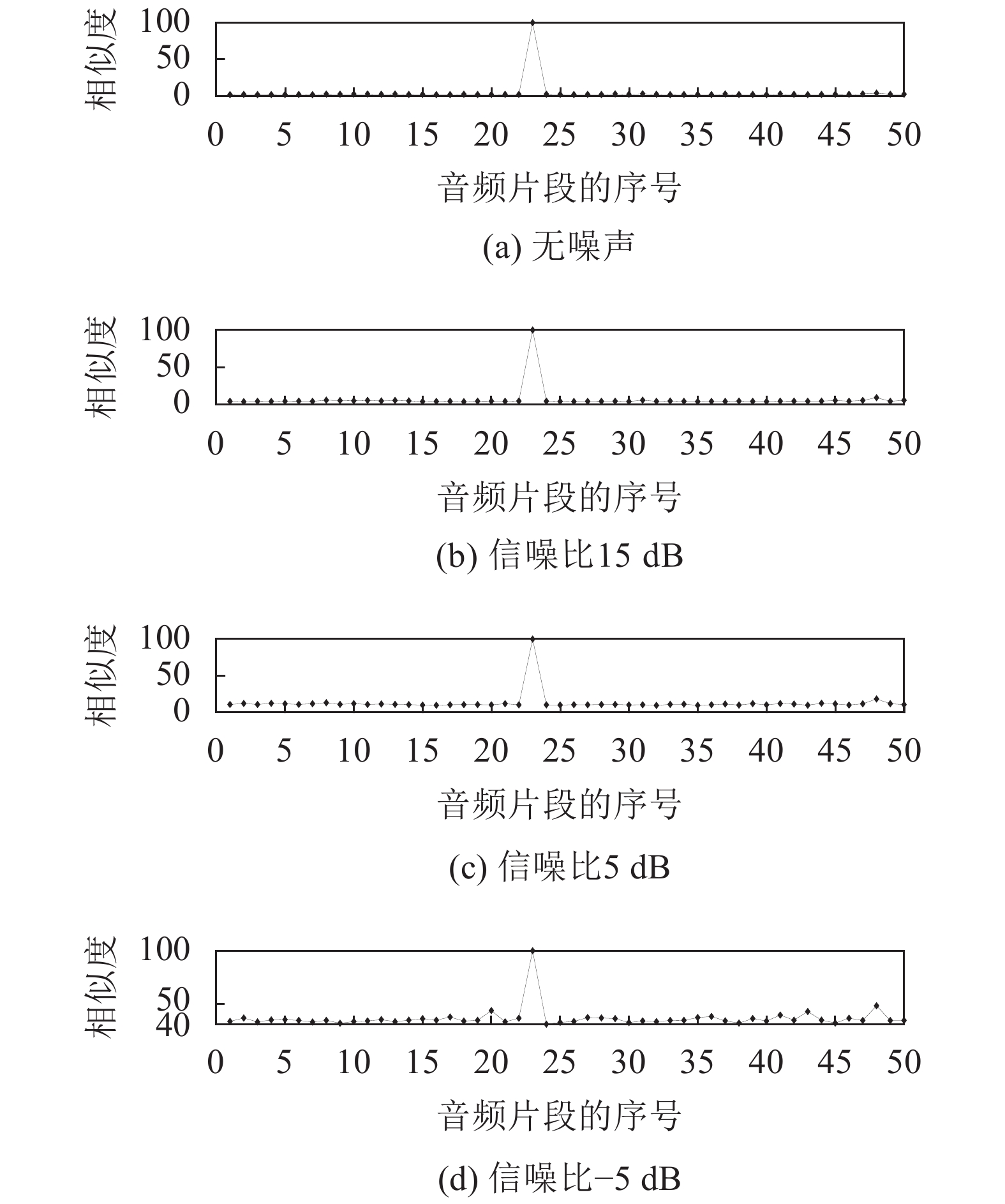 |
| 图5 基于倒谱分析法所测出的相似度 Fig. 5 Similarity based on cepstrum analysis |
从图4可以看出,基于MFCC特征的欧式距离法所测出的欧氏距离在高信噪比(SNR>5 dB)中是有效的,而在低信噪比(SNR=–5 dB)中该方法不能准确地找出相似的音频片段。由图5可知,所提出的倒谱分析法很稳健,即使在低信噪比下也可以找到最佳匹配的音频片段。
3.2.2 比对经过不同通带的带通滤波器处理后的两音频为了模拟两条不同的真实传输链路,设置两个数字带通滤波器a、b,阶数均为8,a的通带为50~2 000 Hz,b的通带为1 500~3 800 Hz,重叠带宽为500 Hz (1 500~2 000 Hz)。将测试样本(第23个)音频经过带通滤波器a处理,模版库中的50个音频分别经过带通滤波器b处理。以第23个音频作为测试样本,与模版库中的50个音频依次用倒谱分析法和欧氏距离法做比对,归一化的欧式距离和相似度结果见图6和7。
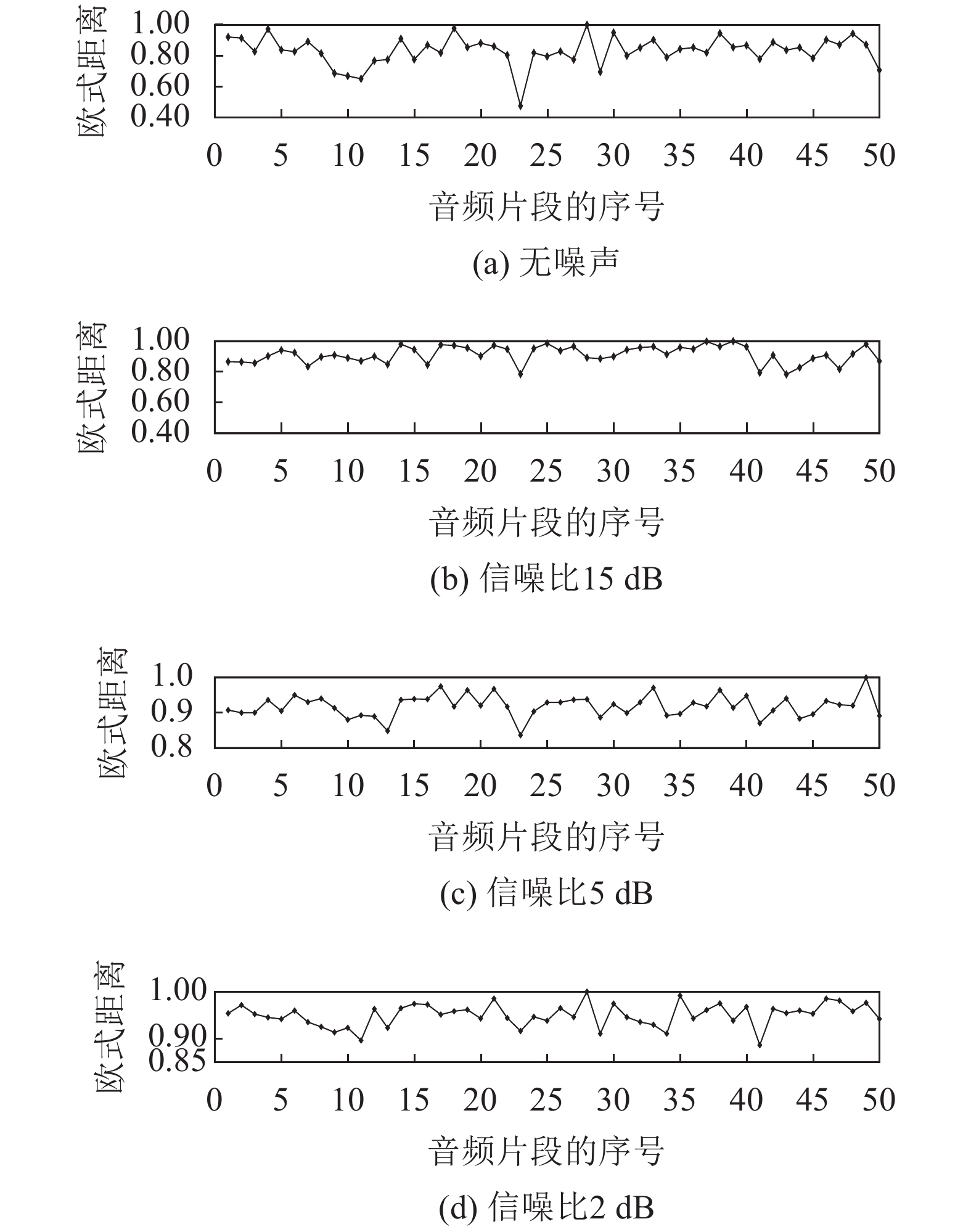 |
| 图6 基于MFCC特征的欧式距离法比对经过不同带宽带通滤波器处理的两音频所测出的欧氏距离 Fig. 6 Euclidean distance measured of two audio processed by different bandpass filters for Euclidean distance method based on MFCC features |
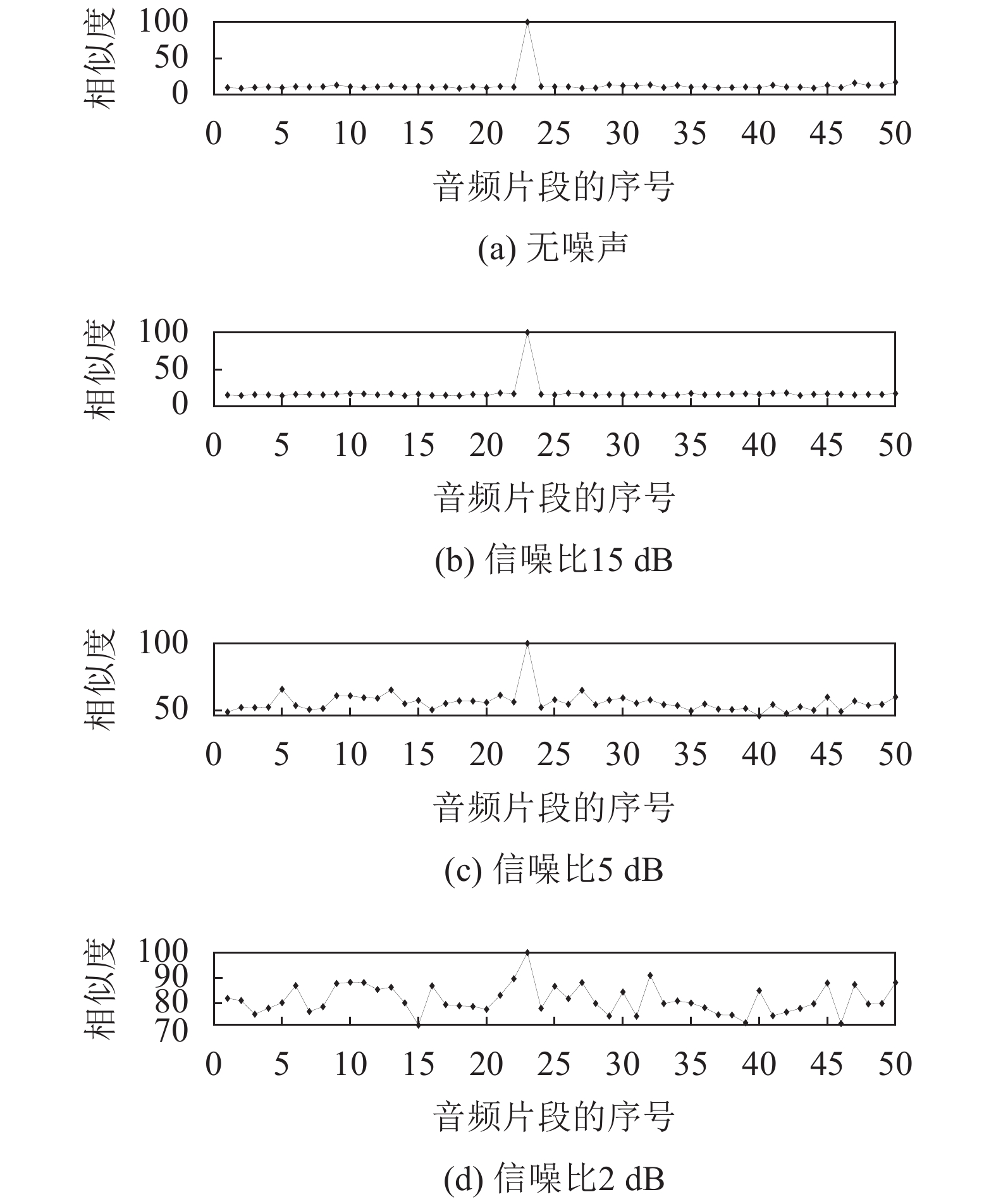 |
| 图7 基于倒谱分析法比对经过不同带宽带通滤波器处理的两音频所测出的相似度 Fig. 7 Similarity between two audio processed by different bandpass filters based on cepstrum analysis |
从图6和7可以看出,待比对的两音频经过不同带宽的带通滤波器处理后,欧氏距离法在无噪声条件下是有效的,而在信噪比(SNR<15 dB)时该方法不能准确地找出相似的音频片段。所提出的倒谱分析法依然非常稳健,即使在低信噪比(SNR=2 dB)时也可以找到正确匹配的音频片段。
3.3 不同信噪比下不同延时两音频延时估计结果和比对结果比较将测试样本(第23个)音频依次加入0.3、2.0、6.0 s这3种不同延时后作为待比对音频
让不同延时的两音频片段在不同信噪比下用所提出的倒谱分析法计算两音频的延时和相似度,结果如图8和9所示,图中,
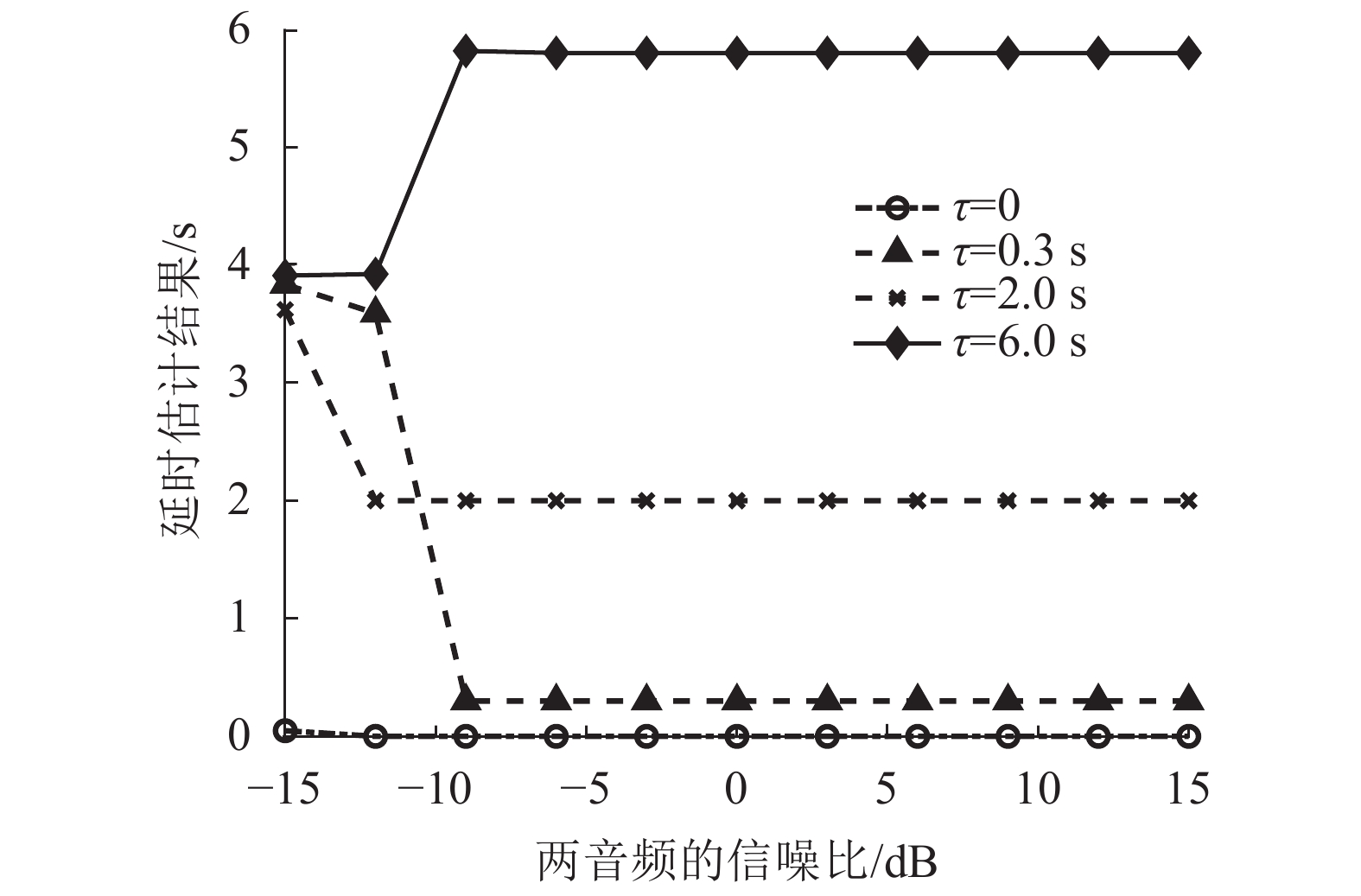 |
| 图8 不同信噪比下两音频延时估计结果 Fig. 8 Results of delay estimation for two audio with different SNR |
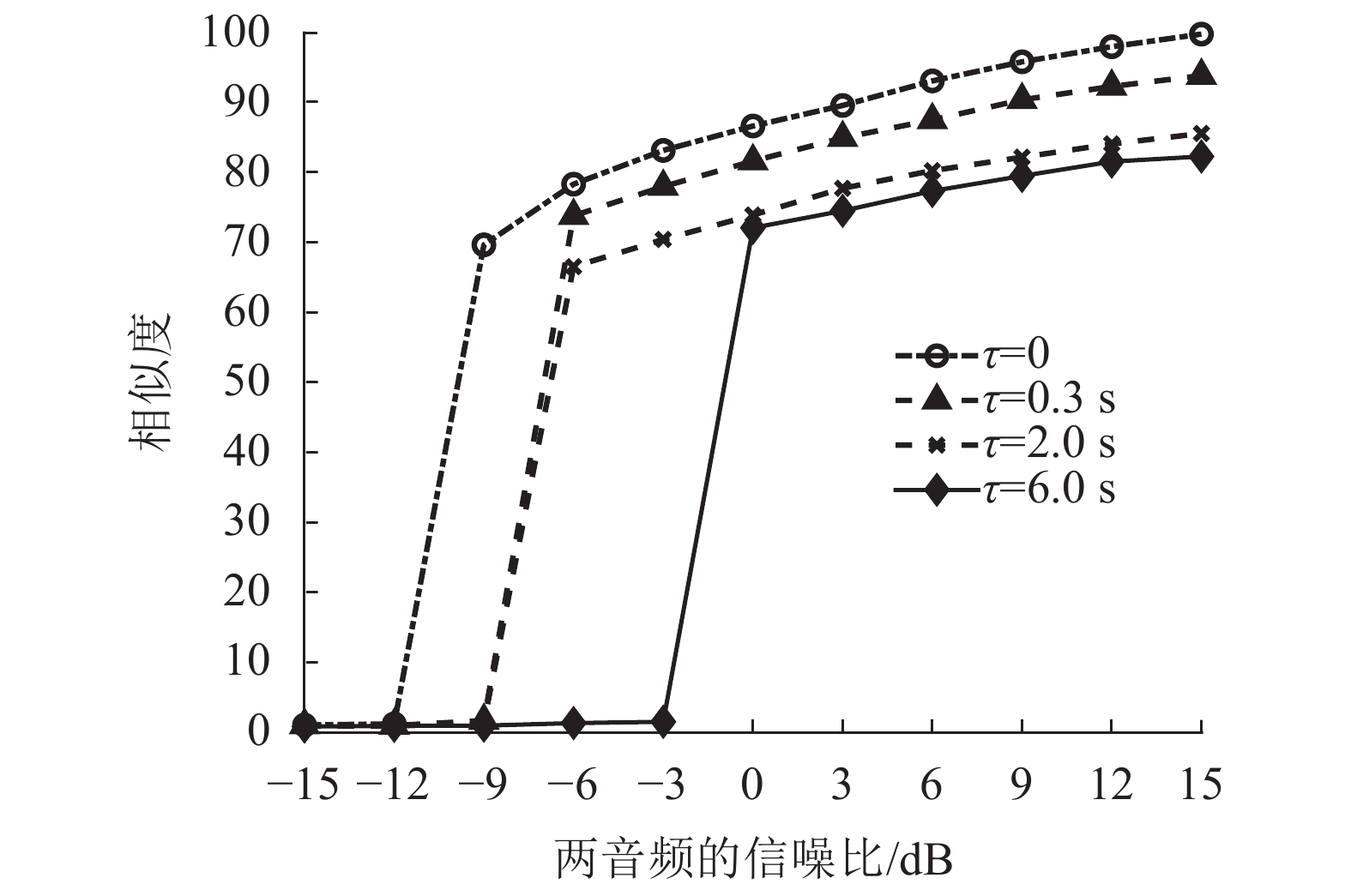 |
| 图9 不同信噪比下两音频相似度比对结果 Fig. 9 Similarity results of two audio with different SNR |
从图8和9可以看出,所提出的倒谱分析法在信噪比较低(–5 dB)时仍可以得到准确的延时估计结果,而相似度会随着两音频延时增加或信噪比降低变得不准确,但是其抗噪声性能仍然在可接受范围内。
3.3.2 不同信噪比下延时估计和比对经过不同通带的带通滤波器处理后的两音频将
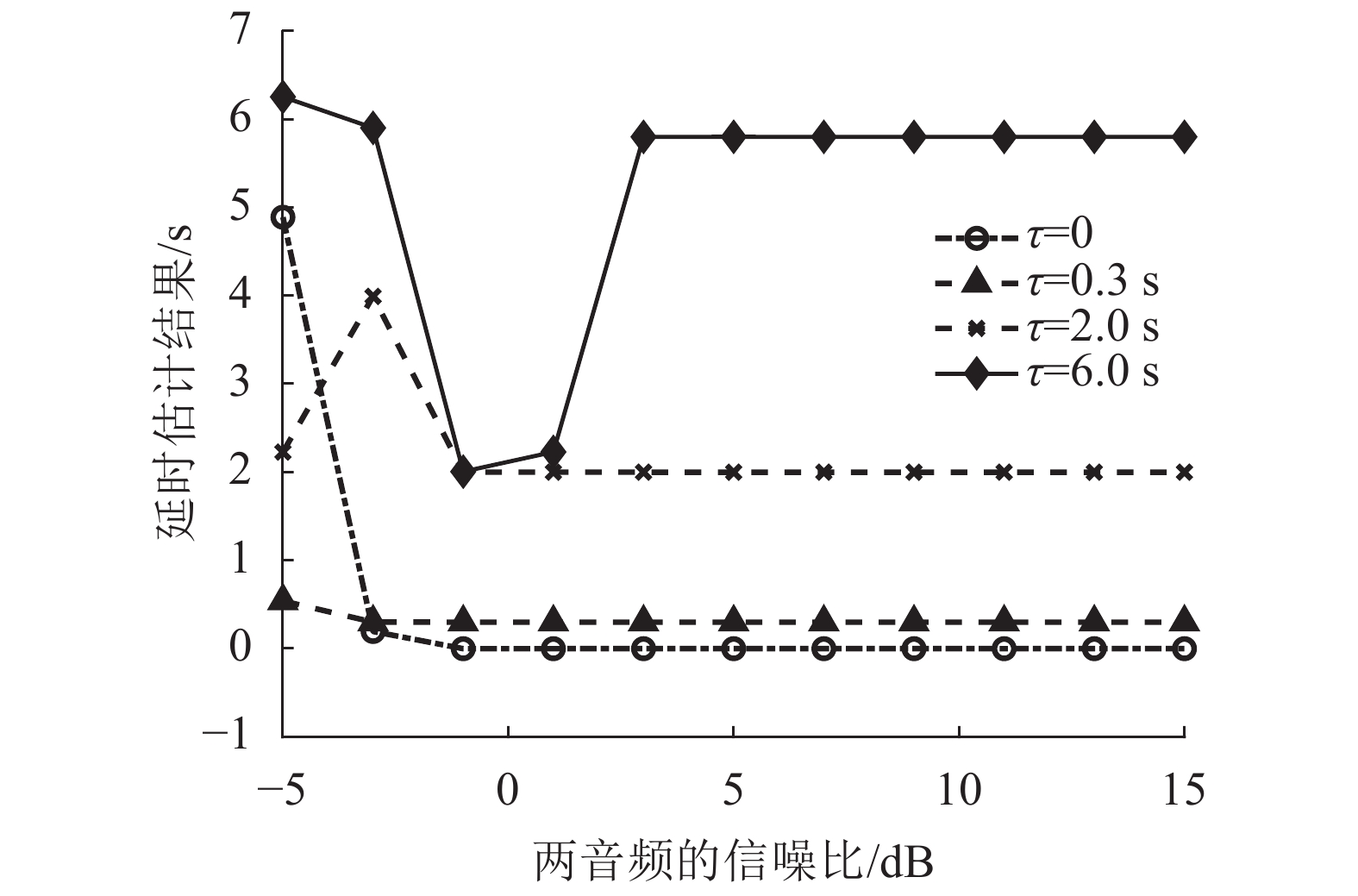 |
| 图10 不同信噪比下经过不同带宽的带通滤波器处理后的两音频延时估计结果 Fig. 10 Results of delay estimation for two audio with different SNR and processed by different bandpass filters |
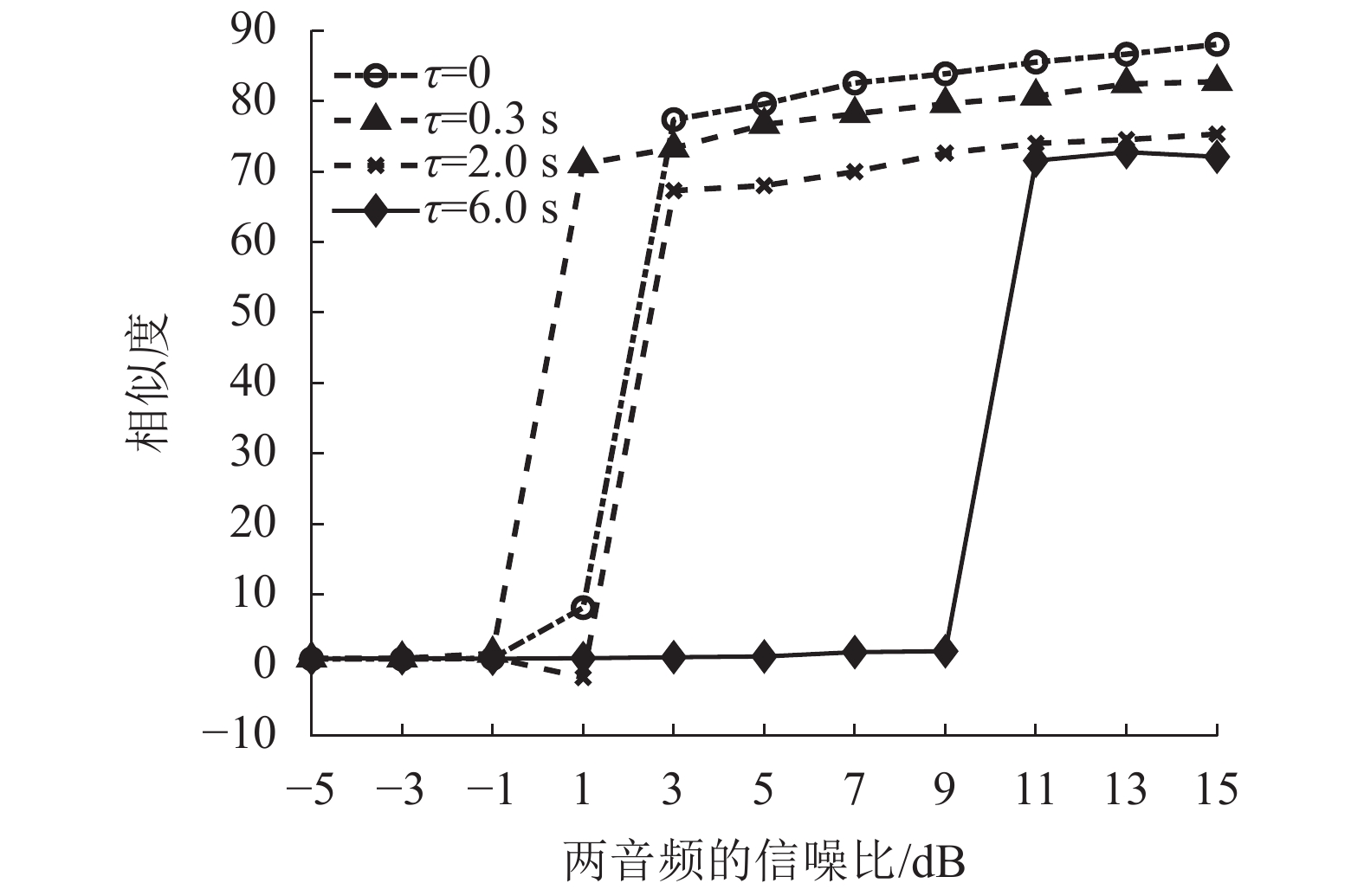 |
| 图11 不同信噪比下经过不同带宽的带通滤波器处理后的两音频相似度比对结果 Fig. 11 Similarity results of two audio with different SNR and processed by different bandpass filters |
3.4 大样本库音频比对
为了验证算法的准确性和鲁棒性,又从50个不同电台总共100 h广播音频源中随机选择了500个音频片段(每个片段持续10 s),其中,包含3种不同语种的语音和各种类型的音乐,如古典、乡村、爵士乐、流行、舞蹈、摇滚等。每个音频片段都经过带通滤波器b处理,同时在每个音频片段中加入加性高斯白噪声,获得不同信噪比的音频片段。500个音频片段依次作为测试样本,先经过带通滤波器a处理,再将其和模版库中的500个音频片段依次计算相似度。匹配精度定义为正确匹配数与音频片段总数之比。比对完成后计算了不同信噪比下所提出倒谱分析法和欧氏距离法的匹配精度,结果如表3所示。
| 表3 不同信噪比下两种方法的匹配精度对比 Tab. 3 Comparison of matching accuracy of two methods under different SNR |
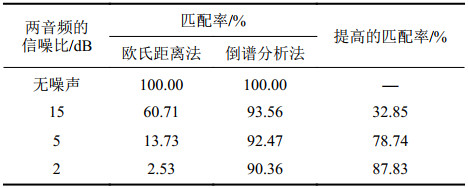 |
如表3所示:当无噪声条件下时,这两种算法可以实现高精度。随着信噪比的降低,欧氏距离法的匹配精度迅速下降,而所提出的算法仍保持可接受的精度。因此可以得出结论,本文提出的倒谱分析法比欧氏距离法得到的音频相似度更准确、更稳健,并且可以在得到相似度结果的同时估计出两音频之间的延时。
3.5 算法运算速度比较为验证算法速度,在同一信噪比(两音频的信噪比为15 dB)、同一实验平台环境下,计算所提出的倒谱分析法和欧氏距离法每次比对所用的时间,如图12所示。由图12可知,所提出的倒谱分析法平均每次运行时间远小于欧氏距离法。其原因是欧氏距离法需要先分别提取两音频的MFCC特征矩阵,再计算两个MFCC特征矩阵之间的欧氏距离,找到最小距离从而得到相似度,因此每次所需要的运行时间就更长。
 |
| 图12 两种方法计算相似度的运行时间 Fig. 12 Average running time of two methods when calculating similarity |
4 结 论
为提高低信噪比和存在延时的两广播音频在实时环境下比对的准确度,提出了一种基于倒谱分析的音频相似度快速计算方法。针对广播音频的特点和音频比对的应用需求,将倒谱分析改进后应用于两音频比对,且计算速度较快,可达到实时比对的要求,能够减少音频相似度错误报警率。该方法不需要对待比对的两音频提取MFCC等音频特征参数,直接通过倒谱分析得出两音频之间的延时估计结果和相似度比对结果。实验结果表明,相比于基于音频特征距离的传统音频比对方法,本文算法的音频比对结果更为准确,同时还能得到延时估计结果。当SNR分别为15、5和2 dB时,本文算法的音频比对匹配精度分别比欧氏距离法提高了32.85%、78.74%和87.83%,每次比对所需要的平均运行时间也缩短。
采用了所提出的倒谱分析音频相似度快速计算方法,有助于提高实时广播音频的比对效率和准确度,大幅度降低音频相似度错误报警率。由于环绕音较强的音频对本文算法性能影响显著,未来将深入研究如何更准确地比对该类型的音频,以进一步提升算法性能。此外,本文算法虽能对两音频进行延时估计,但不能进一步判断出延时的正负情况,如何结合其他算法来达到更准确的延时估计结果也是下一步的研究方向。
| [1] |
Audiovisual, 2019(2): 235-236. [黄思贝. 无线广播电视发射台自动化信号监测系统研究[J]. 视听, 2019(2): 235-236. DOI:10.19395/j.cnki.1674-246x.2019.02.129] |
| [2] |
Communication World, 2019, 26(4): 46-47. [赵洪春. 广播电视发射台监测监控系统设计[J]. 通讯世界, 2019, 26(4): 46-47. DOI:10.3969/j.issn.1006-4222.2019.04.028] |
| [3] |
Liu Chunjiang. Radio program intelligent monitoring system based on audio signal comparison[J]. Radio and TV Broadcast Engineering, 2018, 45(4): 100-104. [刘春江. 基于音频信号比对的无线广播节目智能监测系统[J]. 广播与电视技术, 2018, 45(4): 100-104. DOI:10.16171/j.cnki.rtbe.2018004018] |
| [4] |
Fu Rui,Zhang Dingjing,Niu Tailong,et al. Research on the components of broadcasting monitoring system[J]. China Digital Cable TV, 2019(2): 146-148. [付瑞,张定京,牛泰龙,等. 广播监测系统构成要素研究[J]. 中国有线电视, 2019(2): 146-148. DOI:10.12071/ccatv.2019-02-010] |
| [5] |
原瑾. 数字化中波同步广播单频网的音频时延分析[J]. 数字通信世界, 2018(10): 102. DOI:10.3969/J.ISSN.1672-7274.2018.10.196 |
| [6] |
Zhang Lin,Zhou Tao,Du Qingzhi,et al. Audio comparison algorithm based on physical characteristics[J]. Video Engineering, 2017, 41(11/12): 110-114. [张琳,周韬,杜庆治,等. 基于物理特征的音频相似度比对算法研究[J]. 电视技术, 2017, 41(11/12): 110-114. DOI:10.16280/j.videoe.2017.h11.020] |
| [7] |
Guo Xingji,Fan Bingqi. Feature-based comparison of audio[J]. Journal of Henan Normal University(Natural Science), 2006, 34(2): 35-38. [郭兴吉,范秉琪. 基于特征的音频比对技术[J]. 河南师范大学学报(自然科学版), 2006, 34(2): 35-38. DOI:10.16366/j.cnki.1000-2367.2006.02.009] |
| [8] |
Huang Yuyuan,Yin Ying,Zhao Yue,et al. Acoustic inspection of internal defect in magnetic tile based on bispectrum analysis[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(5): 188-194. [黄沁元,殷鹰,赵越,等. 基于双谱分析的磁瓦内部缺陷音频检测方法[J]. 四川大学学报(工程科学版), 2014, 46(5): 188-194. DOI:10.15961/j.jsuese.2014.05.058] |
| [9] |
Yu Xiaoqing,Pan Xueqian,Yang Wei,et al.Audio similarity measure based on Renyi’s quadratic entropy[C]//Proceedings of the 2010 International Conference on Audio,Language and Image Processing.Shanghai:IEEE,2010:722–726.
|
| [10] |
Sonnleitner R,Widmer G. Robust quad-based audio fingerprinting[J]. IEEE/ACM Transactions on Audio,Speech,and Language Processing, 2016, 24(3): 409-421. DOI:10.1109/TASLP.2015.2509248 |
| [11] |
电子科技大学,北京英夫美迪数字技术有限公司.一种快速广播音频比对方法:CN201510244557.4[P].2015–10–21.
|
| [12] |
Ye Yuqing,Zhang Shaoran,Hong Weijun,et al.Audio similarity comparison system of english dubbing on android platform[C]//Proceedings of the 2017 IEEE International Conference on Information and Automation.Macau:IEEE,2017:692–697.
|
| [13] |
Yao Shanshan,Niu Baoning,Liu Jianquan. Audio identification by sampling sub-fingerprints and counting matches[J]. IEEE Transactions on Multimedia, 2017, 19(9): 1984-1995. DOI:10.1109/TMM.2017.2723846 |
| [14] |
Jaiyen N,Hantula P,Tongta R.Real-time audio similarity comparison algorithm[C]//Proceedings of the 2017 IEEE 15th Student Conference on Research and Development (SCOReD).Putrajaya:IEEE,2017:477–480.
|
 2020, Vol. 52
2020, Vol. 52

