2. 河海大学 江苏省岩土工程技术工程研究中心,江苏 南京 210098;
3. 河海大学 岩土工程科学研究所,江苏 南京 210098;
4. 徐州工程学院 土木工程学院,江苏 徐州 221018;
5. 河海大学 隧道与地下工程研究所,江苏 南京 210098;
6. 南京工程学院 建筑工程学院,江苏 南京 211167
2. Jiangsu Research Center for Geotechnical Eng. Technol., Hohai Univ., Nanjing 210098, China;
3. Research Inst. of Geotechnical Eng., Hohai Univ., Nanjing 210098, China;
4. School of Civil Eng., Xuzhou Univ. of Technol., Xuzhou 221018, China;
5. Research Inst. of Tunnel and Underground Eng., Hohai Univ., Nanjing 210098, China;
6. School of Architecture Eng., Nanjing Inst. of Technol., Nanjing 211167, China
桩土复合路基是高速公路软基路段常用的处理方法,其沉降特性,特别是工后沉降的预测及早期评价尤为重要,对保证营运期的车辆安全与舒适性将起到积极作用[1-3]。许多学者和工程技术人员借助不同方法,对地基工后沉降问题进行了大量研究,并取得了许多有益成果。理论分析方面,Chen等[4]提出考虑初始应力状态影响的高速铁路路基累积沉降分析模型;Shan等[5]建立一种迭代计算方法研究路桥过渡区的不均匀沉降问题;Kermani等[6]提出两种工后沉降预估方法,即利用路基的高度预估工后沉降,以及采用施工过程中压实层的应力–应变行为预测路基的应力–应变–时间变化。数值计算方面,Li等[7]采用弹黏塑性本构模型和有限元程序(CFEM 2D)计算了人工岛的变形和工后沉降;周同和等[8]根据反演出的复合地基变形所需的土层模量放大系数,提出数值模拟计算工后沉降的理论方法;丁铭绩[9]基于数值模拟方法,计算分析了高速铁路CFG桩桩板复合地基设计施工参数等对工后沉降的影响。现场试验方面,Lo等[10]利用前12个月的沉降数据,预测了高速公路9年后的工后沉降;Emadali等[11]采用现代遥感技术监测和预测大坝的工后沉降;陈远洪等[12]基于现场监测数据提出软基路堤工后沉降的幂多项式预测方法。然而,借助施工质量检测方法预测和早期评价桩土复合路基工后沉降情况未见报道。
本文拟在改进现行静载试验方法的基础上,通过采用延时持载手段及概率统计方法,建立一种工后沉降早期检测评价方法。该方法不仅可丰富工后沉降预测的方法,且有利于将现有复合路基质量检测指标体系从单一的强度检测拓展为强度、沉降检测。
1 评价方法为利用桩土复合路基静载试验获取反映工后沉降的信息,进行早期检测评价,除在现行8~10 cm砂垫层上增加弹性垫层模拟实际垫层作用外,引入了延时持载试验手段。
1.1 试验方法改进的必要性在桩土复合路基承载体系中,垫层起着关键作用,现行桩土复合路基静载试验中采用8~10 cm砂垫层模拟实际垫层作用过于简单。基于理论分析、数值模拟计算和室内外试验研究,根据不同桩型,在现有试验条件下,增加对应的弹性垫层,现场试验(图1)结果表明:此方法能较好地模拟实际垫层的作用[13],为获取反映工后沉降的信息提供了可能。
 |
| 图1 应力比值变化试验现场 Fig. 1 Test site of stress ratio change |
理论分析和工程实践表明,在路基荷载和车辆荷载作用下,由于受垫层动态调节的影响,桩土复合路基达到稳定的承载形式,需要有个延迟期。延迟期的长短与垫层的工程性质、桩间距和上部荷载等有关。在广东省交通运输工程质量监督站和佛山市公路桥梁工程监测站的帮助下,作者搜集了广东地区通车2~5年的157段工后沉降实测数据,资料显示:这些复合路基路段的静载试验均满足规范要求,其中包括管桩、水泥搅拌桩、CFG桩、粉喷桩等桩体类型;各路段的通车流量、地层地质组成和填土高度等也不尽相同,具有一定的代表性。采用双曲线法对各路段的工后沉降监测数据进行拟合,预测通车15年的工后沉降。根据预测数据可知,最大的工后沉降为321.15 mm,最小的工后沉降为8.78 mm。以20 mm为组距,共17组,绘制直方图如图2所示。
 |
| 图2 工后沉降直方分布图 Fig. 2 Histogram of post-construction settlement |
由图2可知,工后沉降超过100 mm的路段占总路段的54.78%;有30%以上路段超过规范[14]要求值。数据结果说明:利用静载试验方法在现行试验条件下,易在桩土复合路基未达到稳定的承载形式前试验已结束;加之对垫层作用模拟简单,获取的试验数据很难对工后沉降做出准确的早期检测评价。因此,要获取桩土复合路基稳定承载形式下的试验数据,实现早期检测评价,有必要完善现行静载试验对垫层的模拟,引入延时持载试验手段。
1.2 评价关系式在改进现行试验方法的基础上,通过对不同现场延时持载试验结果的分析,并考虑垫层调节作用的影响时间,在延时持载试验过程中,采用双曲线法[15]拟合沉降–时间关系,即:
| ${S\!_t} = {S\!_0} + \frac{{t - {t_0}}}{{a + b\left( {t - {t_0}} \right)}}$ | (1) |
式(1)可改写为:
| $\frac{{\Delta t}}{{\Delta S}} = \frac{{t - {t_0}}}{{{S\!_t} - {S\!_0}}} = a + b\left( {t - {t_0}} \right)$ | (2) |
式中:
对式(1)求极限可得持载状态下的最大残余沉降
| ${S\!_{{\rm{r}}\;\max }} = \frac{1}{b}$ | (3) |
对式(1)求导可得持载试验的沉降速率Vt,即:
| ${V_t} = \frac{{\partial S}}{{\partial t}} = \frac{a}{{{{\left[ {a + b\left( {t - {t_0}} \right)} \right]}^2}}}$ | (4) |
将
| $ {S\!_{{\rm{r}}\;\max }} \le {S\!_{{\rm{r}}t}},{V_t} \le {V_{{\rm{r}}t}} $ | (5) |
式中,Srt、Vrt为评价指标,可根据规范[14]中不同路段15年工后累计沉降要求(桥头过渡路段小于100 mm,含结构物路段小于200 mm,一般路段小于300 mm)换算而得。基本思路如下:假设检测路段所有桩体的沉降特性相同,并以路堤截面中心点沉降值为对应评价指标的换算值,采用概率统计方法分析,建立路堤截面中心点沉降值与延时持载试验值的对应关系,最终确定评价指标。
桩土复合路基是否处于稳定的承载状态,可通过分析桩土应力比变化情况判断,即在荷载作用下桩土应力比需趋于稳定。对于复合路基桩土应力比变化,许多学者和工程技术人员已经开展了相关性研究[16-19],并取得了有益的结论。综合现场资料和理论分析可知:当静载荷试验加载到较大值时,可使垫层的调节速率增大,在短时间内达到实际荷载下的稳定桩土应力比值。通过理论分析、数值计算及现场试验(图1、3)等方法研究了桩土应力比在不同荷载和时间下的变化规律,结果表明:90%的情况在2倍承载力设计值延时48 h内,复合路基的桩土应力比可达实际荷载下的稳定桩土应力比值。因此,在延时持载试验中,取2倍承载力设计值,并延长48 h,将由此获取的
 |
| 图3 试验现场加载及百分表布置 Fig. 3 Site loading and dialgage layout |
2 评价参数
评价关系式中,工后沉降评价参数
延时持载试验是引入弹性垫层并在常规静载荷试验的基础上进行的改进,因此试验主要参数可参考《建筑地基处理技术规范》(JGJ79—2012)[20]。具体试验步骤包括前期准备、加载及沉降–时间关系观测和数据提取等部分。
1)试验荷载确定及加载分级。确定复合路基承载力设计值,并取2倍值作为试验设计荷载,与常规单桩复合路基静载试验的最大载荷相同。根据规范[20]要求,加载分8~12级,并控制每一级加载时间间隔。
2)试验垫层选择。为更好地模拟垫层的调节作用,采用8~10 cm砂垫层+弹性橡胶垫层,弹性橡胶垫层厚度h和弹性模量E的取值见表1[13]。
| 表1 弹性橡胶垫层参数取值 Tab. 1 Elastic rubber cushion parameter values |
 |
3)试验加载装置的布置。试验采用压重平台反力装置。压重平台反力装置作为荷载反力,将大于最大试验荷载的荷重在试验开始前一次性加上平台;试验时,用液压千斤顶分级加载。荷载板一般采用直径1.26 m、面积1.25 m2的圆板,见图3。
4)数据采集设备布置。在压板四角装设4个百分表,按规定时间测定沉降量,百分表精度为0.01 mm。
5)沉降–时间关系观测。加载阶段按规范要求记录数据;延时持载阶段测读沉降量前6次时间间隔依次为10、10、10、15、15、15 min,以后每隔30 min测读一次沉降量。
6)数据提取分析。从采集的试验数据中提取延时持载下各时间点对应的沉降值,根据式(1)或(2)对持载过程不同时间点沉降数据进行双曲线拟合,获取
按延时持载试验步骤,取3个典型现场试验路段,说明
| 表2 典型现场试验路段工况 Tab. 2 Working conditions of typical field test sections |
 |
| 表3 典型路段代表性试验数据 Tab. 3 Representative test data of typical sections |
 |
根据式(2),设
 |
| 图4 拟合曲线 Fig. 4 Fitting curves |
根据图4的拟合直线可获取各工况的
| 表4 各工况现场试验S–t关系式的参数 Tab. 4 Parameters of S–t relations in field tests under various working conditions |
 |
将表4中的数据代入式(1)中,可得各工况对应的S–t关系式,即:
| $S = {S\!_{0}}{\rm{ + }}\frac{{t - {t_{0}}}}{{{a} + {b}(t - {t_{0}})}}$ | (6) |
由式(4)可得t=t0时的沉降速率
| 表5 典型路段现场试验评价指标计算结果 Tab. 5 Calculation results of field test evaluation indexes for typical sections |
 |
3 评价指标
评价关系式中,评价指标Srt、Vrt由搜集的157段复合路基工后沉降实测数据和38段静载延时持载试验实测数据,通过概率统计分析方法,建立对应关系;再根据不同路段规范要求的工后沉降值,确定建议值。
3.1 工后沉降分布特点分析根据相关研究[21-22]和对已搜集路段的工后沉降资料分析,设桩土复合路基最终工后沉降
| $f\left( c \right) = \frac{1}{{c\sqrt {2\text{π} } \sigma }}{{\rm{e}}^{ - \frac{{{{\left( {\ln\; c - \mu } \right)}^2}}}{{2{\sigma ^2}}}}}$ | (7) |
令
| ${\!\!\! \textit{z}} = \frac{{\ln c - \mu }}{\sigma }$ | (8) |
可得标准正态分布形式。根据密度函数和正态分布定义,工后沉降累计分布函数为:
| ${F_{\rm{g}}}\left( c \right) = \varPhi \left( {\textit{z}} \right) = P\left( {{\textit{Z}} \le {\textit{z}}} \right) = \int_{{\rm{ - }}\infty }^{\textit{z}} {\frac{1}{{\sqrt {2\text{π} } }}} {{\rm{e}}^{ - \frac{1}{2}{{\textit{z}}^2}}}{\rm{d}}{\textit{z}}$ | (9) |
其中
| $\!\!\!\!\!\!\!\!\!\hat \mu = \frac{1}{n}\sum\limits_{i = 1}^n {\ln\; {c_i}} $ | (10) |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\hat \sigma ^2} = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {\ln\; {c_i} - \frac{1}{n}\sum\limits_{i = 1}^n {\ln\; {c_i}} } \right)} ^2}$ | (11) |
式中,n为实测路段个数,本文取n=157。由157个路段的复合路基工后沉降实测数据,可求得
采用非参数假设检验,即
| $\nu = \sum\limits_{i = 1}^k {\frac{{{{\left( {{n_i} - n{{\hat p}_i}} \right)}^2}}}{{n{{\hat p}_i}}}} $ | (12) |
式中:
| ${\hat p_i} = P\left\{ {{c_{i - 1}} \le C \le {c_i}} \right\} = {F_0}\left( {{c_i}} \right) - {F_0}\left( {{c_{i - 1}}} \right)$ | (13) |
| ${\hat p_i} \approx \varPhi \left( {\frac{{\ln\; {c_i} - \hat \mu }}{{\hat \sigma }}} \right) - \varPhi \left( {\frac{{\ln\; {c_{i - 1}} - \hat \mu }}{{\hat \sigma }}} \right)$ | (14) |
从而得
| $ \chi _{0.25}^2\left( {14} \right) = 17.117 \le \nu \le \chi _{0.10}^2\left( {14} \right) = 21.064{\text{。}} $ |
即工后沉降分布有90%的可能性服从对数正态分布,其分布参数
38组不同桩型、不同试验条件下,加载过程中的沉降和最大残余沉降如图5所示。
 |
| 图5 加载过程沉降与残余沉降 Fig. 5 Loading process and maximum residual settlement |
由图5可知:加载过程中沉降分布在95.32~3.80 mm之间,最大残余沉降分布在38.760~0.299 mm之间。沉降最大值发生在24#试验上,沉降最小值发生在1#试验上。从数据的分布形式上看,最大残余沉降在不同取值区间分布规律略有不同,最终沉降也有类似现象。
3.2.1 采用对数正态分布分析设最大残余沉降
| $ {F_{\rm{r}}}\left( {{s_{{\rm{r}}\;\max }}} \right) = \varPhi \left( {\textit{z}} \right) = P\left( {{\textit{Z}} \le {\textit{z}}} \right) = \int_{{\rm{ - }}\infty }^{\textit{z}} {\frac{1}{{\sqrt {2\text{π} } }}} {{\rm{e}}^{ - \frac{1}{2}{{\textit{z}}^2}}}{\rm{d}}{\textit{z}} $ | (15) |
假设
| $\chi _{0.25}^2\left( 4 \right) = 5.385 \le \nu \le \chi _{0.10}^2\left( 4 \right) = 7.779{\text{。}} $ |
即
首先采用Γ–分布分析,设
设
| $\frac{1}{{{S\!_{{\rm{r}}\;\max }}}}{\text{~}}\Gamma \left( {\alpha ,\beta } \right)$ | (16) |
式中,
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f\left( {{s_{{\rm{r}}\;\max }}} \right) = \frac{{{\beta ^\alpha }}}{{\Gamma \left( \alpha \right)}}{s_{{\rm{r}}\;\max }}^{ - \alpha {\rm{ - }}1}{{\rm{e}}^{ - \frac{\beta }{{{s_{_{{\rm{r}}\;\max} }}}}}}$ | (17) |
| ${F_{\rm{r}}}\left( {{s_{{\rm{r}}\;\max }}} \right) = \int_0^{{s_{{\rm{r}}\;\max }}} {f\left( x \right)} {\rm{ d}}x$ | (18) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{{\hat \beta }}{{\hat \alpha {\rm{ - }}1}} = \frac{1}{m}\sum\limits_{k = 1}^m {{s_{{\rm{r\;max}}k}}} $ | (19) |
| $\frac{{{{\hat \beta }^2}}}{{{{\left( {\alpha {\rm{ - }}1} \right)}^2}\left( {\alpha {\rm{ - }}2} \right)}} = \frac{1}{m}{\sum\limits_{k = 1}^m {\left( {{s_{{\rm{r\;max}}k}} - \frac{1}{m}\sum\limits_{k = 1}^m {{s_{{\rm{r\;max}}k}}} } \right)} ^2}$ | (20) |
式中:m为延时持载试验次数,取m=38;k=1,2,
假设
| $\nu \ge \chi _{0.005}^2\left( 5 \right) = 16.750{\text{。}} $ |
即最大残余沉降有99.5%的可能性服从逆Γ–分布,其形状参数
综上分析,延时持载试验在持载状态下,最大残余沉降分布服从对数正态分布和逆Γ–分布的可能性均很高。为判断二者的区别,分别做最大残余沉降的实测值及服从对数正态分布和逆Γ–分布时的概率密度函数曲线,如图6所示。
 |
| 图6 最大残余沉降概率分布 Fig. 6 Probability distribution of Sr max |
由图6可知,对数正态分布和逆Γ–分布的差异主要发生在数据分布段上。即:最大残余沉降值大于7.0 mm且小于12.0 mm采用逆Γ–分布拟合更好;小于7.0 mm或大于12.0 mm采用对数正态分布拟合更好。
3.3 评价指标确定 3.3.1 评价指标由于检测试验是随机选择的,因此,可假设检测路段所有桩体的沉降特性相同。虽然实际路段的工后沉降受控因素较多,涉及有车辆荷载、加固区、下卧层等方面,但可假设工后沉降反映的是承载形式特性。由上述结果的进一步分析可知,桩土复合路基实际发生的工后沉降与延时持载试验的最大残余沉降呈正相关,反映到概率分布上可认为:延时持载试验的最大残余沉降发生的概率与实际工后沉降发生的概率有对应关系,即:将通车15年工后沉降规范要求值100 mm(桥头过渡路段)、200 mm(含结构物路段)和300 mm(一般路段),代入式(9),查阅标准正态分布表,即可得到不同路段满足规范要求的概率
| 表6 最大残余沉降检测标准 Tab. 6 Maximum residual settlement test standard |
 |
与上述分析方法相同,作
 |
| 图7 参数a概率分布 Fig. 7 Probability distribution of a |
对a的试验结果进行概率分布拟合,得:
| $F\left( a \right) = 1 - 1.87{\rm{exp}}\left( { - \frac{a}{{4.36}}} \right)$ | (21) |
由表6的计算结果,联立式(21)、(3)和(4),可得到延时持载试验沉降速率Vt=48 h的评价指标值,见表7,其含义同表6。
| 表7 延时持载试验沉降速率Vt=48 h评价指标值 Tab. 7 Test standard of delayed load holding test settlement rate Vt=48 h |
 |
考虑到实际情况的多样性,建议采用双评价指标值控制,目的是最大限度保证能获取复合路基稳定承载状态下的工后沉降评价信息。
值得指出的是,在工后沉降分布特点分析和最大残余沉降分布特点分析中,样本数量仍然偏少,给出的评价指标准确性还有提升空间。另外,除采用概率统计方法获取延时持载试验的最大残余沉降与实际工后沉降对应关系外,还可以采用一些确定值的理论或数值分析方法描述。考虑到本文着重提出一种新的早期检测评价方法和基本分析思路,故不再赘述。
3.3.2 实例分析在搜集资料中,选择了资料较完整的3个路段(试验编号为4#、19#、38#),其中,4#、19#试验路段于2015年7月建成通车,38#试验路段于2016年12月建成通车。具体设计施工参数如表8所示。
| 表8 试验路基设计施工参数 Tab. 8 Test roadbed design construction parameters |
 |
在改进现行试验条件的延时持载试验中,采集的数据如表9所示。
| 表9 延时持载试验数据 Tab. 9 Time-delay holding test data |
 |
各路段工后沉降监测频率如表10所示,获取的工后沉降数据如图8所示。
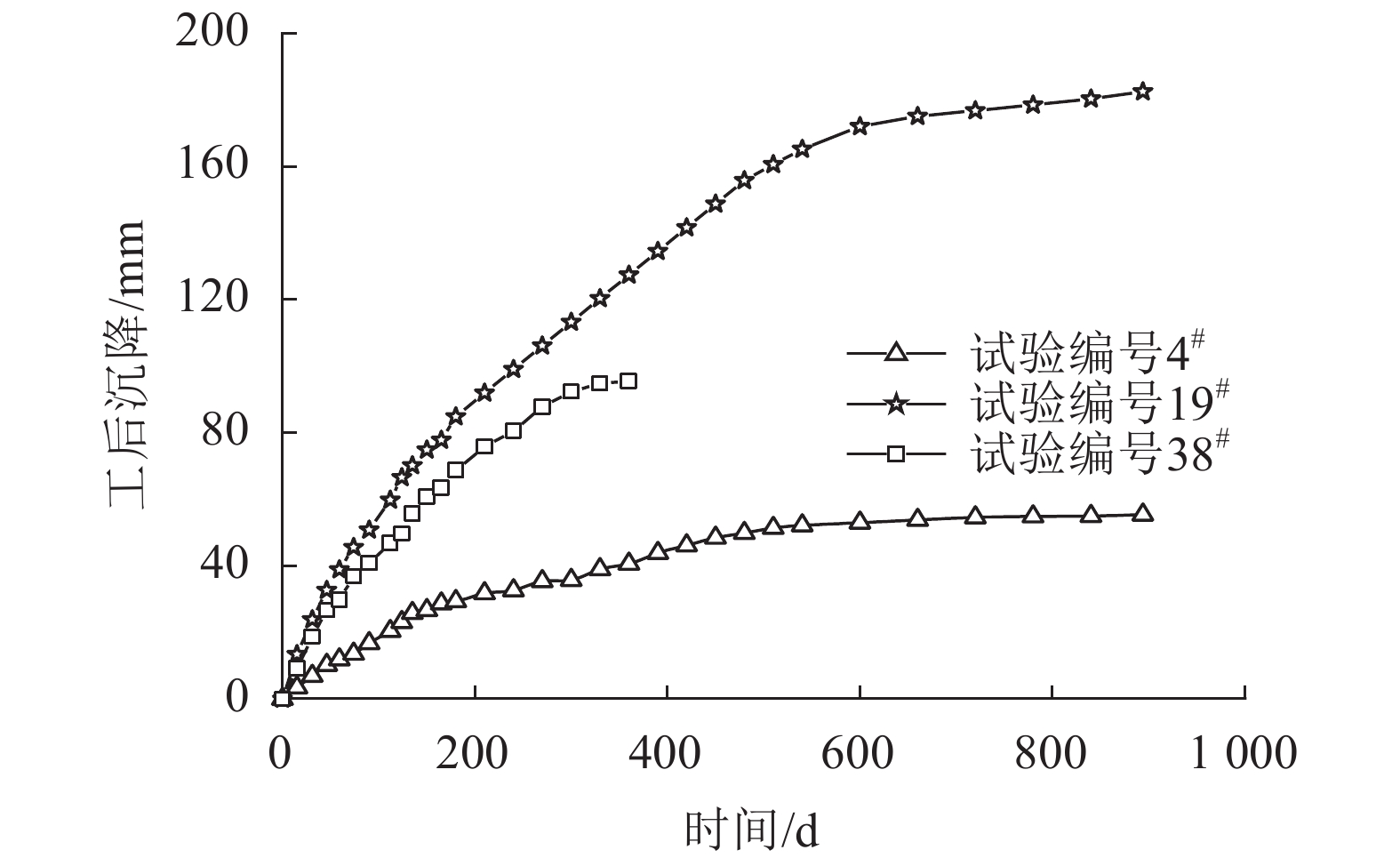 |
| 图8 工后沉降实测数据 Fig. 8 Post-contruction settlement measuring data |
| 表10 工后沉降实测频率 Tab. 10 Measuring frequency of post-construction settlement |
 |
延时持载试验最大残余沉降及工后15年各方法计算的工后沉降见表11。
| 表11 工后沉降计算结果 Tab. 11 Post-work settlement calculation results |
 |
各计算结果与实测数据工后沉降预测值(双曲线法)的误差情况如表12所示。
| 表12 计算结果的误差分析 Tab. 12 Error analysis of the calculated results |
 |
根据分析结果,结合表6、7的评价指标值,以及延时持载最大残余沉降实测累计概率密度曲线(图6),分别与服从对数正态分布和逆Γ–分布时的累计概率密度曲线拟合分析,验证了最大残余沉降值在小于7.0 mm或大于12.0 mm时,采用服从对数正态分布;大于7.0 mm且小于12.0 mm时,采用服从逆Γ–分布,对工后沉降进行评价和预估。即可通过利用延时持载试验结果达到评价桩土复合路基工后沉降的目的。
在第2.2节的典型现场试验分析中,前2个路段,即:水泥搅拌桩复合路基现场试验(4#)、CFG桩复合路基现场试验Ⅰ(14#),均满足
1)在桩土复合路基延时持载试验中,延时持载残余沉降
2)采用概率统计分析方法,通过不同实测数据对比可知,延时持载试验的最大残余沉降值小于7.0 mm或大于12.0 mm采用对数正态分布拟合准确性更高;大于7.0 mm且小于12.0 mm采用逆Γ–分布拟合准确性更高。
3)15年工后沉降规范要求值为100 mm(桥头过渡路段)、200 mm(含结构物路段)和300 mm(一般路段)时,延时持载试验最大残余沉降
4)实例表明,对延时持载试验评价指标值不满足评价关系式要求的桩土复合路基,应根据实际情况进行后续的补救措施,如:注浆、超载预压和延长预压时间等处理,可避免大的工后沉降。
| [1] |
Eid H T,Shehada A A. Estimating the elastic settlement of piled foundations on rock[J]. International Journal of Geomechanics, 2015, 15(3): 04014059. DOI:10.1061/(asce)gm.1943-5622.0000376 |
| [2] |
Li Guowei,Nguyen T N,Amenuvor A C. Settlement prediction of surcharge preloaded low embankment on soft ground subjected to cyclic loading[J]. Marine Georesources & Geotechnology, 2016, 34(2): 154-161. DOI:10.1080/1064119x.2014.985860 |
| [3] |
Li Haibin,Zheng Xianglei,Sheng Yanping,et al. Differential settlements of embankment treated by cement fly-ash gravel pile and sheet pile in freeway extension constructions[J]. International Journal of Geomechanics, 2017, 17(11): 04017092. DOI:10.1061/(asce)gm.1943-5622.0000995 |
| [4] |
Chen R P,Jiang P,Ye X W,et al. Probabilistic analytical model for settlement risk assessment of high-speed railway subgrade[J]. Journal of Performance of Constructed Facilities, 2016, 30(3): 04015047. DOI:10.1061/(asce)cf.1943-5509.0000789 |
| [5] |
Shan Yao,Zhou Shunhua,Zhou Hechao,et al. Iterative method for predicting uneven settlement caused by high-speed train loads in transition-zone subgrade[J]. Transportation Research Record:Journal of the Transportation Research Board, 2017, 2607(1): 7-14. DOI:10.3141/2607-02 |
| [6] |
Kermani M,Konrad J M,Smith M. An empirical method for predicting post-construction settlement of concrete face rockfill dams[J]. Canadian Geotechnical Journal, 2017, 54(6): 755-767. DOI:10.1139/cgj-2016-0193 |
| [7] |
Li Gang,Zhang Jinli,Yang Qing,et al. Centrifugal test and numerical assessment for settlement of a large-scale artificial island constructed on deep marine clays[J]. European Journal of Environmental and Civil Engineering, 2017, 21(2): 172-192. DOI:10.1080/19648189.2015.1110054 |
| [8] |
Zhou Tonghe,Guo Yuancheng,Zhang Sihua,et al. Prediction and control of post-construction settlement for post-processing dual compound foundation[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(增2): 42-46. [周同和,郭院成,张四化,等. 后处理二元复合地基工后沉降预测与控制技术[J]. 岩土工程学报, 2010, 32(增2): 42-46.] |
| [9] |
Ding Mingji. Numerical simulation on the post-construction settlement of CFG pile-slab composite foundation in high-speed railway[J]. China Railway Science, 2008, 29(3): 1-6. [丁铭绩. 高速铁路CFG桩桩板复合地基工后沉降数值模拟[J]. 中国铁道科学, 2008, 29(3): 1-6. DOI:10.3321/j.issn:1001-4632.2008.03.001] |
| [10] |
Lo S,Mak J,Gnanendran C T,et al. Long-term performance of a wide embankment on soft clay improved with prefabricated vertical drains[J]. Canadian Geotechnical Journal, 2008, 45(8): 1073-1091. DOI:10.1139/T08-037 |
| [11] |
Emadali L,Motagh M,Haghshenas Haghighi M. Characterizing post-construction settlement of the Masjed-Soleyman embankment dam,Southwest Iran,using TerraSAR-X SpotLight radar imagery[J]. Engineering Structures, 2017, 143: 261-273. DOI:10.1016/j.engstruct.2017.04.009 |
| [12] |
Chen Yuanhong,Chen Zhan,Zhou Ge. Power-polynomial prediction and analysis of post-construction settlement of embankment on soft ground[J]. China Civil Engineering Journal, 2009, 42(5): 112-116. [陈远洪,陈占,周革. 软基路堤工后沉降的幂多项式预测与分析[J]. 土木工程学报, 2009, 42(5): 112-116. DOI:10.15951/j.tmgcxb.2009.05.001] |
| [13] |
Xu Fenqiang.Study on the bearing characteristics and new testing method of pile-soil composite embankment[D].Nanjing:Hohai University,2017. 徐奋强.桩土复合路基承载特性与检测新方法研究[D].南京:河海大学,2017. |
| [14] |
中华人民共和国交通运输部.公路软土地基路堤设计与施工技术细则:JTG/T D31-02—2013[S].北京:人民交通出版社,2013.
|
| [15] |
Wang Wei,Zai Jinmin,Lu Tinghao. Analysis on hyperbolic model and exponential model for post-construction settlement of soft soil[J]. Journal of Jiangsu University(Natural Science Edition), 2008, 29(2): 173-176. [王伟,宰金珉,卢廷浩. 软土工后沉降双曲线模型与指数曲线模型分析[J]. 江苏大学学报(自然科学版), 2008, 29(2): 173-176.] |
| [16] |
Zhou Longxiang,Wang Mengshu,Zhang Dingli,et al. Study of the soil arching effect and the pile-soil stress ratio of composite ground[J]. China Civil Engineering Journal, 2011, 44(1): 93-99. [周龙翔,王梦恕,张顶立,等. 复合地基土拱效应与桩土应力比研究[J]. 土木工程学报, 2011, 44(1): 93-99. DOI:10.15951/j.tmgcxb.2011.01.017] |
| [17] |
Zhao Minghua,Ma Binhui,Zhang Ling. Analysis of time effect of pile-soil stress ratio in gravel-pile composite foundation[J]. Journal of Central South University(Science and Technology), 2008, 39(4): 831-837. [赵明华,马缤辉,张玲. 碎石桩复合地基桩土应力比的时效分析[J]. 中南大学学报(自然科学版), 2008, 39(4): 831-837.] |
| [18] |
Lü Weihua,Miao Linchang. Calculation method of pile-soil stress ratio of rigid pile composite foundation[J]. Journal of Southeast University(Natural Science Edition), 2013, 43(3): 624-628. [吕伟华,缪林昌. 刚性桩复合地基桩土应力比计算方法[J]. 东南大学学报(自然科学版), 2013, 43(3): 624-628. DOI:10.3969/j.issn.1001-0505.2013.03.032] |
| [19] |
Zhao Minghua,Niu Haoyi,Liu Meng,et al. Pile-soil stress ratio and settlement of composite ground with gravel piles in flexible foundation[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1549-1556. [赵明华,牛浩懿,刘猛,等. 柔性基础下碎石桩复合地基桩土应力比及沉降计算[J]. 岩土工程学报, 2017, 39(9): 1549-1556. DOI:10.11779/CJGE201709001] |
| [20] |
中华人民共和国住房和城乡建设部.建筑地基处理技术规范:JGJ 79—2012[S].北京:中国建筑工业出版社,2012.
|
| [21] |
夏乐天.应用概率统计[M].北京:机械工业出版社,2008.
|
| [22] |
Liu Xin,Gan Liangqin,Sheng Ke,et al. Experimental study on service life of foamed mixture lightweight soil based on method of accelerated stress tests[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1793-1799. [刘鑫,甘亮琴,盛柯,等. 基于加速应力试验方法的气泡混合轻质土使用寿命估计研究[J]. 岩土工程学报, 2017, 39(10): 1793-1799. DOI:10.11779/CJGE201710006] |
| [23] |
Qin Weiliang,Qin Li,Da Qingli. The computation of VaR based on the normal inverse gamma distribution and general extreme value distribution[J]. Application of Statistics and Management, 2008, 27(2): 250-256. [秦伟良,秦莉,达庆利. 基于正则逆Gamma分布和广义极值分布的VaR计算[J]. 数理统计与管理, 2008, 27(2): 250-256. DOI:10.13860/j.cnki.sltj.2008.02.021] |
 2020, Vol. 52
2020, Vol. 52


