2. 中国北方车辆研究所,北京 100072
2. China North Vehicle Research Inst., Beijing 100072, China
随着中国实现各种装置设备从引进仿制到自主研制的过渡,需要进行动态压力测量的场合和需求也变得越来越多,尤其在航空航天发动机领域对高频动态压力的高精度测量与校准显得尤为突出。如航空发动机研制与测试中,高速旋转的叶片会在发动机压气机内形成15~22 kHz的脉动压力[1-2];在新型脉冲爆震发动机(PDE)的性能研究实验中发现,爆震室内除了与爆震频率一致的50 Hz以内的脉冲压力外,每次爆震还可能引起频率达10 kHz以上的压力振荡[3-4];在评价弹药毁伤效能中,爆炸冲击波超压测试空中爆炸压力冲击波上升时间一般在亚毫秒到微秒级,要求测量系统或传感器的固有频率至少在100 kHz以上,测量带宽至少达到10 kHz以上[5-6]。对于上述这些高频动态压力参数的测量不仅关系到装备性能的好坏,还是重要的设计和优化依据,这就离不开高精度的高频正弦压力的测量与校准。
目前国内外高频动态压力校准主要采用激波管校准的方式[7-8],但激波管压力阶跃过程的测量溯源一直没有得到解决,通过现有算法等得到的幅频响应和相频响应只具有定性意义,无法进行不确定度分析。以正弦压力为代表的周期性压力校准能对压力测试系统动态特性进行定量评价,但其可靠溯源问题一直没有得到解决,目前基本还是使用参考传感器的比较法形式进行溯源,而参考传感器的量值溯源问题同样存在,并且国际上很大部分研究人员更倾向于把这类基于比较法建立的装置当成专用的测试设备而不是计量标准设备,因此正弦压力校准中的可溯源问题成为其使用推广中的瓶颈[9]。同时现有正弦压力校准频率低于10 kHz[10],并不能满足很多高频动态压力测试校准需要,还需要往上拓展正弦压力校准频率范围。
作者介绍国防科技工业第一计量测试技术中心研制的激光干涉法高频液体正弦压力校准装置,采用压电换能器在密闭管腔中激励液体介质产生正弦压力,再利用激光干涉法测量液体折射率随压力变化的方法用于正弦压力校准,压力改变液体介质折射率的激光干涉法正弦压力幅值测量实现了正弦压力的可靠溯源[11],并对压力分布、温度、结构形变、振动等误差来源进行了分析与实验。
1 基本原理与结构激光干涉法高频液体正弦压力校准采用压电换能器作为正弦压力发生器,压电换能器由压电陶瓷叠堆构成,当压电叠堆由设定的交流信号驱动时,压电叠堆表面就会产生相应的位移变化,此时压电叠堆可以等效为一个运作的活塞[12],推动密闭管腔内液体介质产生正弦压力,由管道动力学分析建立压力与液体折射率和光程的关系模型,并通过激光干涉仪精密测量液体光程的改变,从而实现基于激光干涉技术的正弦压力的测量,并将动态压力溯源到长度、时间、质量等基本量上,其核心结构原理如图1所示。
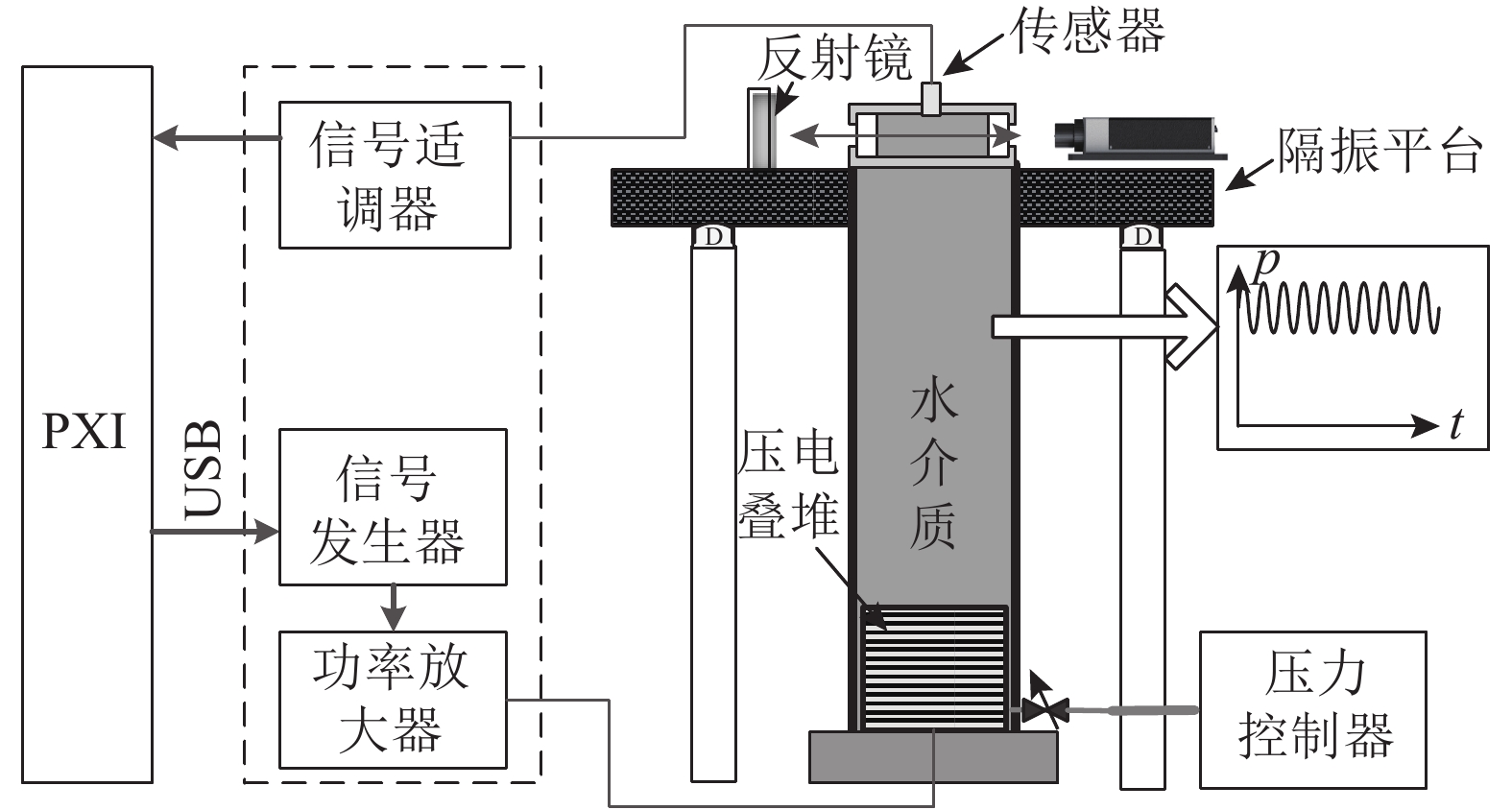 |
| 图1 激光干涉法高频液体正弦压力校准示意图 Fig. 1 Schematic diagram of high frequency liquid sinusoidal pressure calibration by laser interferometry |
激光干涉法高频液体正弦压力校准装置除了核心的高频液体压力发生器与激光干涉测量系统外,还包括静压控制系统、数据采集分析及控制系统、地基与光学隔振平台等部分。在进行正弦压力激光干涉测量中,压力传感器安装在测量段侧壁上感受正弦压力,数据采集分析及控制系统同步采集传感器电压信号与激光干涉仪信号,在同一段时间内,传感器测量的电压信号与经过测量模型计算得到的压力信号作比,即可得到压力传感器的动态灵敏度曲线。
2 高频液体正弦压力发生器高频液体正弦压力发生器主要包括压电叠堆系统和谐振管腔系统两大部分,压电叠堆系统负责产生正弦激励,而谐振管腔系统负责放大激励信号。由于压电叠堆具有逆压电效应[13],压电叠堆由设定频率的电压信号驱动时,在其表面会产生和驱动电压频率一致的位移。由于在管腔内部液体介质的不可压缩性,压电叠堆的位移迫使液体介质传递与激励频率相同的压力波,当激励频率与谐振管腔的固有频率一致时,整个系统进入共振状态,在管腔的另一端就可以得到经过共振放大的正弦压力波。
实际谐振管腔和压电叠堆是个较复杂的机电耦合系统[14],其性能受多方面因素的影响,如实际应用中压电叠堆粘结层的材料性质会影响其输出位移、整体结构上存在反谐振点、安装缝隙、液体介质内混有气体等,一定程度上都会影响谐振频率的大小和产生压力的幅值。
为了实现装置在整个频率范围内都产生较好正弦压力波和适当的幅值,装置设计了双压电叠堆形式并进行结构优化实现频率范围的扩展,构建的管腔结构基于在每1 kHz整数倍附近出现谐振实现幅值的增大,提高信噪比,并在管腔中段建立光学测量段,装置主体结构如图2所示。
 |
| 图2 高频液体正弦压力校准装置 Fig. 2 High frequency liquid sinusoidal pressure calibration device |
3 正弦压力激光干涉测量 3.1 测量原理
为了实现基于激光干涉技术的正弦压力光学测量,需要把激光干涉测量系统得到的运动参数(位移、速度、加速度)转化为压力变化。采用纯水为液体压力介质,在光频条件下,根据洛伦兹–洛伦茨方程(Lorentz-Lorenz equation)[15],非导电液体介质的折射率n与密度ρ之间存在一定关系。从定性的角度上,折射率n随着密度ρ的增大而增大,密度ρ与压力p、温度T存在复杂的函数关系;从定量的角度上,在50 MPa以内的等温过程中,可推导出折射率n与压力p近似为线性关系。在20 ℃条件下,进行线性拟合可以得到水的折射率模型公式为:
| $n = {K_{\rm{w}}}p + {n_{20}}$ | (1) |
式中:
在光学测量段中,利用激光干涉测量高频液体状态改变,但实际的测量光路如图3所示,总测量光程路径
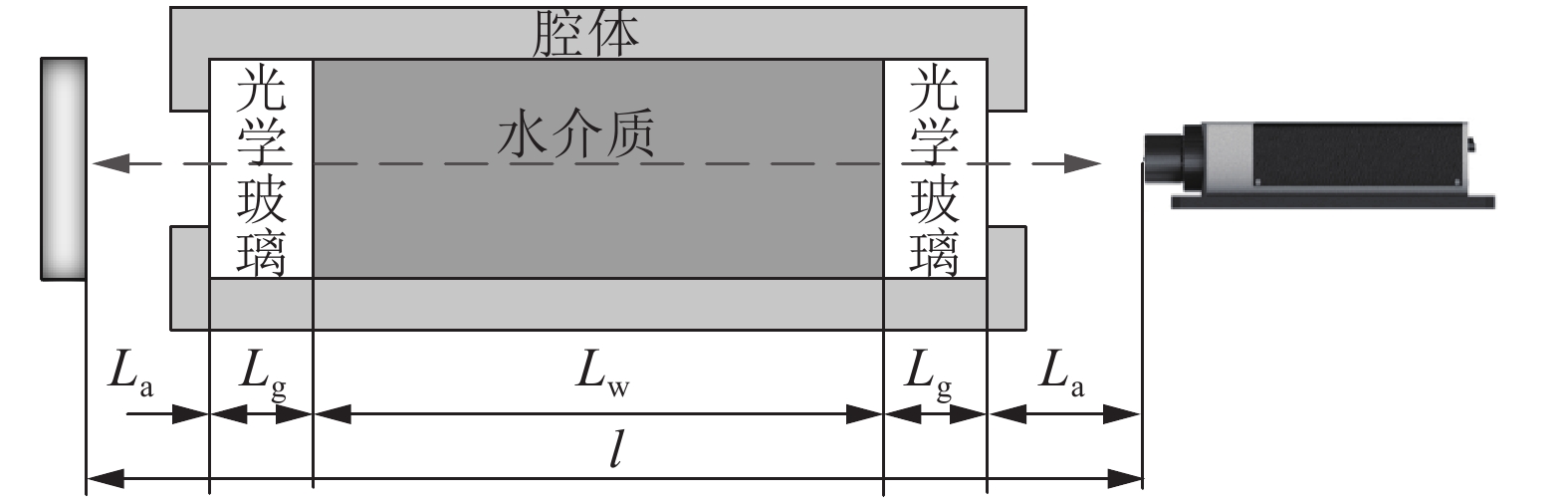 |
| 图3 测量光路示意图 Fig. 3 Schematic diagram of measuring optical path |
| $l = 2{L_{\rm{a}}} + 2{L_{\rm{g}}} + {L_{\rm{w}}}$ | (2) |
式中,
光学测量段主要由光学玻璃和金属腔体构成。光学玻璃采用H–K9L型玻璃,弹性模量
| $\Delta l = \Delta {L_{\rm{w}}} = \Delta n{L_{\rm{w}}} = {K_{\rm{w}}}\Delta p{L_{\rm{w}}}$ | (3) |
由此得到光程–压力的数学模型,其中光程–压力转化系数定义为压力激光测量的光程灵敏度a为:
| $a = {{\Delta l} / {\Delta p}} = {K_{\rm{w}}}{L_{\rm{w}}}$ | (4) |
由式(4)可见,光程灵敏度a与液体介质的中光程
现场原位静态标定的方式来确定光程灵敏度具有两点优势:首先,不需要对液体介质的中光程路径进行测量,极大的提高了实验的便利性;其次,只要液体介质的相关物理属性不发生突发性的或本质性的变化,动态校准实验前的原位静态标定可以消除其相关物理属性长期漂移带来的影响。
正弦压力的幅值
| $\Delta {p_{\rm{m}}} = {{\Delta {l_{\max }}} / a}$ | (5) |
式中,
在建立光程–压力数学模型和利用式(5)计算正弦压力幅值的过程中,都进行了不同程度的简化,这些简化在实际测试和计算中都可能导致测量误差的引入。因此,需要对可能存在的误差源进行分析和补偿,主要体现在以下几个方面:
1)压力分布不均
压电叠堆产生的压力波在液体介质中传递和反射,由于谐振管腔内部的不可见性,使得腔体内的压力分布情况不易掌握。实际校准中,被校传感器安装与激光光路测量垂直,存在一小段位置差,传感器感压面与激光干涉测量系统测量到的一个点的压力p可能存在不一致。
采用基于有限元法的声场数值模拟方法,能够直观地得到流体声场在某一频率下的声压分布,计算激光光路上的压力与被校传感器感受到的压力之间的偏差,根据分析结果,在10 kHz以内,激光光路上与传感器敏感中心的幅值最大相对偏差为0.8%,相位相对偏差估计小于1.0º;10~20 kHz两点之间的幅值最大相对偏差为2.1%,相位相对偏差估计小于2.5º;20~30 kHz两点之间的幅值最大相对偏差为3.0%,相位相对偏差估计小于3.3º。
2)温度变化
在动态压力过程中,等温过程并不适用。正弦压力持续时间仅仅数毫秒并且伴随腔内液体体积的压缩和膨胀,可假设在此过程中液体与腔体无实质性热交换,应当将其考虑为一个绝热过程。
绝热情况下的温度变化与体积膨胀和压缩,在现有的温度测量方法上,这些变化在毫秒量级上无法得到可靠的测量。因此,有必要联系绝热过程中温度的改变与压力的变化上去。
对比在等温过程和绝热过程中,折射率与温度和压力的关系,可得知温度变化导致的相对偏差在0.3%~1.2%之间。
3)结构形变
在压力环境下,压力载荷作用在光学玻璃和腔体结构上的影响主要表现为在内部压力介质的作用下产生挤压变形,使得激光测量的光程发生变化。采用有限元法来解决光结构变形量,得到光学玻璃与腔体在不同频率正弦压力激励和不同压差下的形变量,从而可以进一步分析光程的变化。
对于腔体结构,通过ANSYS结构仿真分析得到在0~10 MPa载荷下,激光测量路径的管腔整体形变量达到0.0844 μm/MPa,其中主要关注的横向形变占比达95%。管腔受静态压力的形变量会影响激光干涉测量的准确度,对于长度14 mm的内径光学路径,理论计算得到的光程灵敏度a为2.4025 μm/MPa,对于测量通道所在的测量段的形变对于激光干涉测量的影响最大达到3.34%。
对于光学玻璃,通过加载10 MPa静载荷压力可知,光学玻璃最大变形在中央处为1.19 μm,外边缘变形最小,通过1~30 kHz的仿真,结果显示玻璃轴向形变动态幅值在0.1~1.0 μm之间,那么光学玻璃可能产生的最大形变量影响达到2.09%。
4)振动
在实际动态测量中,激光测量光路不仅通过液体介质,还将通过外界空气与光学玻璃。由于密封和保护玻璃片的需要,光学玻璃的设计一般使用端面加密封垫圈的形式,压电叠堆的工作会造成光学玻璃的振动,这种振动也会造成激光通过液体介质的物理路径变化。
激光测量到的光程的变化主要来自于两个主要因素:液体介质折射率变化与光学玻璃的振动移动。假设振动位移
如果只考虑单边光学玻璃,光学玻璃的轴向振动引起的光程偏差约为
通过多次实验确定在0~10 kHz范围内光写玻璃相对振动很小,光学玻璃振动对测量误差影响也很小,引起的幅值误差不超过0.6%,相位误差小于0.4°,在10~25 kHz的范围内光学玻璃相对振动相比低频段略有增加,引起的幅值误差最大值为1.4%,25 kHz以上光学玻璃片相对振动幅值误差不超过3.2%。
3.3 激光干涉测量实验首先需要原位标定的光程灵敏度a,设计的腔体内长度L=14 mm,光程灵敏度a理论值为2.4025 μm/MPa,通过原位标定得到实际装置的光程灵敏度a为2.3302 μm/MPa。
利用搭建的高频液体正弦压力装置进行了正弦压力激光干涉测量实验。采用外差式激光干涉仪Polytec–OFV505测量腔体内液体介质光程的改变,干涉仪位移档位设定为1 μm/V。实验中同步采集压力传感器测量输出信号与激光干涉仪测量位移输出信号,激光干涉仪测量结果根据式(5)计算得到压力信号。某次5 kHz正弦压力激励下实验中同步采集的压力传感器输出信号与激光干涉仪测量计算的压力信号的比对结果,如图4所示。
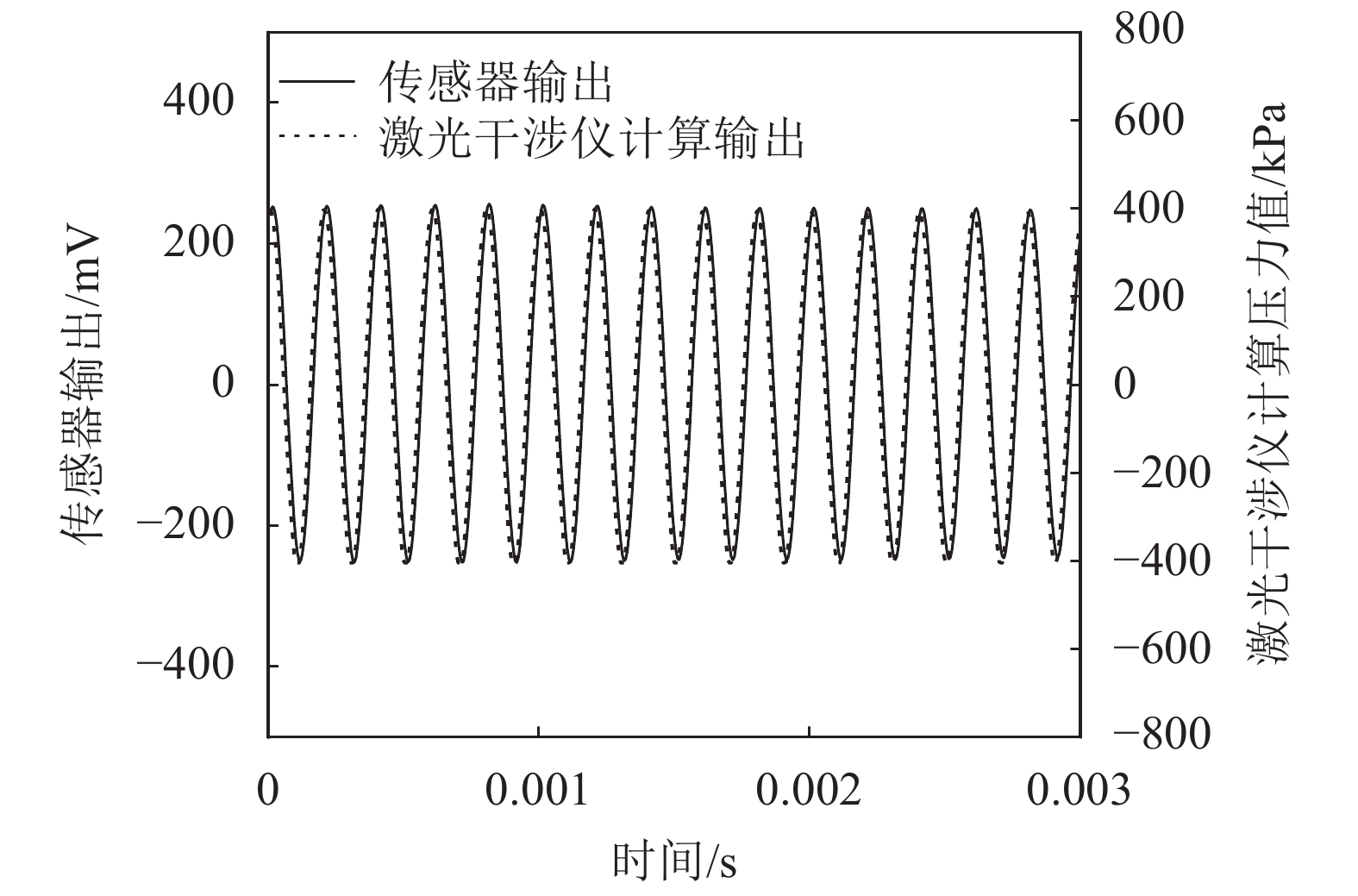 |
| 图4 5 kHz正弦压力下输出曲线 Fig. 4 Output curve under sinusoidal pressure of 5 kHz |
可见激光干涉测量并解算动态压力工作正常,压力波形与压力传感器输出波形基本一致,基于激光干涉法测量液体动态压力变化历程的方法切实可行。
4 系统实验与不确定度分析 4.1 校准实验激光干涉法高频液体正弦压力校准装置主要由高频液体正弦压力发生器,激光干涉测量系统和数据采集分析系统三大部分构成,整体装置实验部分如图5所示。
 |
| 图5 校准装置实验图 Fig. 5 Experimental diagram of calibration device |
高频液体正弦压力发生器安装在大理石隔振基座上,光学测量段穿过开孔光学平台,激光干涉测量系统安装在光学平台上,通过光学测量段测量管腔内部压力变化。上述布置目的是避免压电叠堆工作所带来的振动影响,振动会影响激光干涉系统对正弦压力信号的测量。
选定PCB 113B26型传感器进行校准实验,传感器出厂校准参数如表1所示。
| 表1 PCB 113B26 出厂校准参数 Tab. 1 Calibration parameters of PCB 113B26 |
 |
对选定传感器进行校准实验,在1~30 kHz范围内挑选频率间隔为1 kHz的30个谐振频率点进行校准,得到传感器在这一频率范围内动态幅值灵敏度并与其出厂校准的灵敏度进行比较,如图6所示。
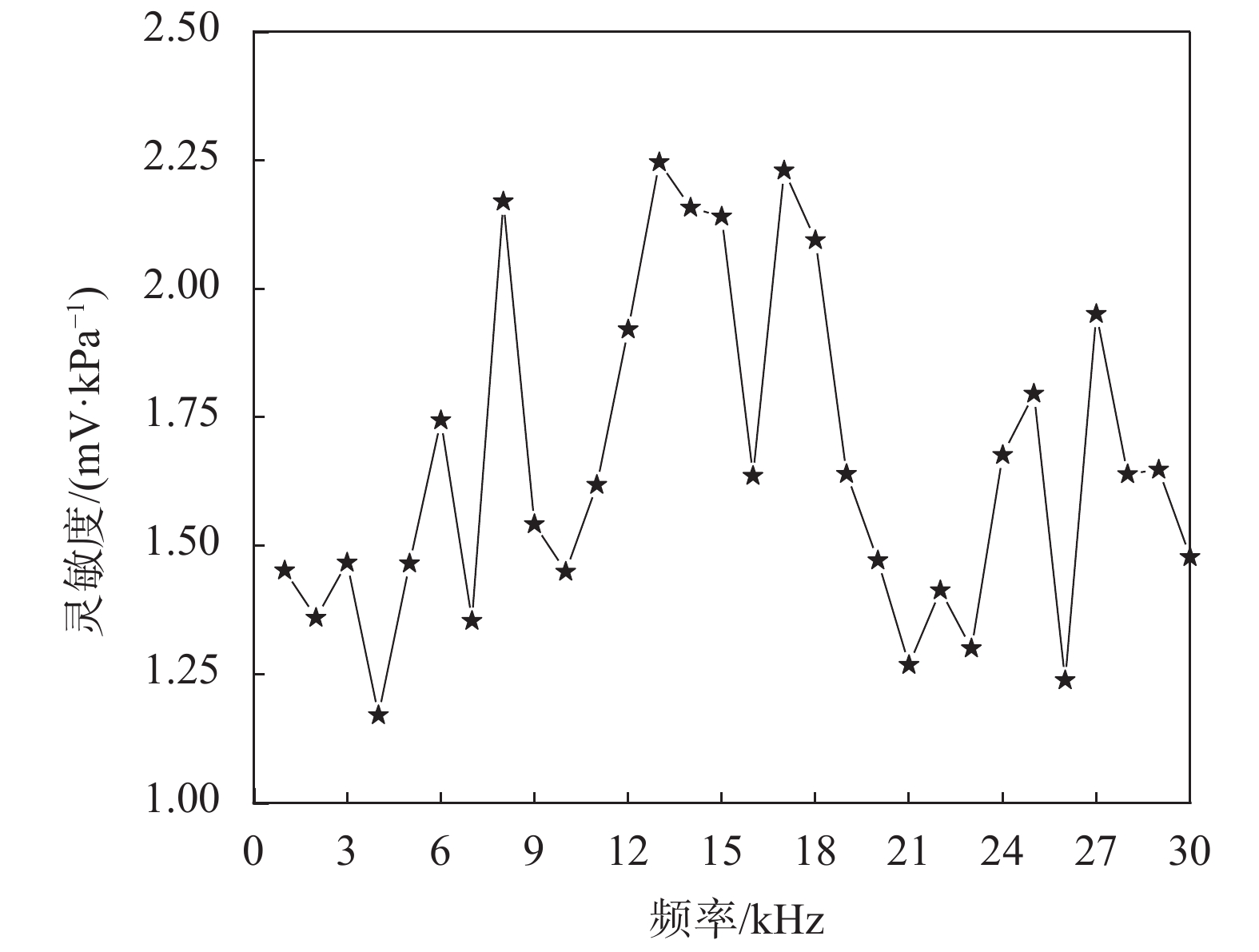 |
| 图6 谐振点下幅值灵敏度曲线 Fig. 6 Amplitude sensitivity curve at resonance point |
某些频点下的动态幅值灵敏度与静态灵敏度之间偏差较大,可能原因:一是由于校准装置自身存在反谐振点导致信噪比降低;二是由于传感器自身动态特性决定。
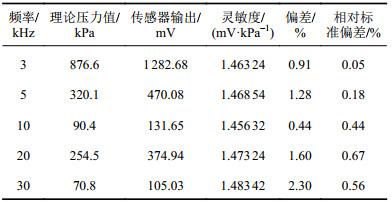
抽取几组频点进行传感器校准,在每一频点下进行8次校准,校准结果如表2所示。30 kHz频率下校准传感器的幅值灵敏度与静态灵敏度偏差最大为2.30%,每个频点下进行8次重复校准,幅值灵敏度的相对标准偏差均较小,最大为0.67%,证明装置的重复性较好。
| 表2 校准结果 Tab. 2 Calibration results |
 |
4.2 幅值灵敏度校准不确定度分析
被校传感器幅值灵敏度为:
| $S = \frac{{\Delta U}}{{\Delta {P_{\rm m}}}} = \frac{{\Delta U \cdot a}}{{\Delta {l_{\max }}}}$ | (6) |
式中,
幅值灵敏度校准不确定度影响量包括激光干涉位移测量、光程灵敏度、压力分布、结构形变、振动、温度、数据采集分析系统、测量重复性等。
1)被测电压采集引入的不确定度分量。根据数据采集卡校准证书(10 kHz以内交流幅值校准)以及依据《数据采集系统校准规范》(JJF 1048—1995)进行的频率扩展与相位自校准实验结果表明,在0~10 kHz频率范围内,电压采集引入的幅值相对误差在0.05%以内;在10~30 kHz频率范围内,电压采集引入的幅值相对误差在0.25%以内。上述相对误差服从均匀分布,故电压采集带来的不确定度分量估计为:
| $u\left( {{x_1}} \right) = 0.002\;5/\sqrt 3 = 0.14{\text{%}} $ | (7) |
2)激光干涉仪位移测量引入的不确定度分量。根据激光干涉仪的校准证书,10 kHz以内激光干涉仪硬件解调的幅值误差小于0.2%,10~20 kHz小于0.3%,20~30 kHz小于0.6%。上述误差服从均匀分布,则激光干涉仪位移测量引入的不确定度分量为:
| $u\left( {{x_2}} \right) = 0.006/\sqrt 3 = 0.35{\text{%}} $ | (8) |
3)压力激光测量的光程灵敏度引入的不确定度分量。压力激光测量的光程灵敏度a通过原位标定以及数学模型
| $u\left( {{x_3}} \right) = \sqrt {{{0.001\;2}^2} + {{0.006}^2}} = 0.61{\text{%}} $ | (9) |
4)温度变化引入的不确定度分量。根据前述的温度影响分析,温度改变所带来的最大测量误差为1.2%,服从均匀分布,则温度变化引入的不确定度分量为:
| $u\left( {{x_4}} \right) = 0.012/\sqrt 3 = 0.69{\text{%}} $ | (10) |
5)结构形变引入的不确定度分量。根据上述结构形变影响因素分析与实验,测量通道所在的测量段的形变对于激光干涉测量的影响最大达到3.34%,服从均匀分布,其引入的不确定度为
| $u\left( {{x_5}} \right) = \sqrt {0.0{\rm{1}}{{\rm{9}}^2} + 0.0{\rm{1}}{{\rm{2}}^2}} = {\rm{2}}.{\rm{2}}{\text{%}} $ | (11) |
6)光学窗口振动引入的不确定度分量。根据上述振动影响因素分析与实验,光学窗口振动引起的最大幅值测量误差估计为0.6%(10 kHz以内)、1.4%(10~20 kHz)与3.2%(20~30 kHz),服从均匀分布,则该不确定度分量为:
| $u\left( {{x_6}} \right){\rm{ }} = 0.03{\rm{2}}/\sqrt 3 = {\rm{1}}.{\rm{8}}{\text{%}} $ | (12) |
7)压力分布不均引入的不确定度分量。根据上述影响因素分析与实验,激光测量光路与传感器敏感中心的幅值最大相对偏差在1~10 kHz为0.8%;10~20 kHz两者之间的幅值最大相对偏差为2.1%;20~30 kHz两者之间的幅值最大相对偏差为3.0%,服从均匀分布,则该不确定度分量为:
| $u\left( {{x_7}} \right){\rm{ }} = 0.030/\sqrt 3 = 1.73{\text{%}} $ | (13) |
8)多次测量重复性引入的不确定度分量。10 MPa下,在30 kHz频率下经过10次实验,利用贝塞尔公式计算,取幅值灵敏度相对标准偏差的最大值,则引入的A类不确定度分量为
在10 MPa静态压力环境,30 kHz频率下扩展不确定度为:
| $U(S) = 2 \times \sqrt {\sum\limits_{i = 1}^7 {u{{({x_i})}^2} + u_{\rm{A}}^2} } = 7.6{\text{%}} $ | (14) |
通过在10 MPa静态压力下,1~30 kHz频率范围内的多次不同频率下幅值灵敏度校准不确定度分析,扩展不确定度在3.0%~7.6%(k=2)。
5 结 论基于激光干涉测量技术的高频液体正弦压力校准装置,可以通过压力腔内液体介质激光光程的变化复现腔内压力的变化历程,利用激光干涉仪取代参考传感器,使长度基本量直接复现动态压力单位量值,也避免了参考传感器的溯源问题,实现了动态压力的绝对校准。
校准装置实现正弦压力的可靠溯源,并能够产生频率范围为1~30 kHz,动态幅值范围为0.01~1.00 MPa的正弦压力,校准装置的扩展不确定度在7.6%以内,在某些频率和非谐振频率下还存在信噪比较低的情况,严重影响校准结果,因此还需进一步提高和完善。
基于激光干涉测量的高频液体正弦压力校准技术及装置,未来可应用于压力幅值宽且频率含量丰富的液体动态压力测量当中,也为中国未来动态压力测量和校准技术领域的研究和探索提供了一定依据。
| [1] |
Yang Xueguang,Zhang Xiaoguang,Xing Zhiguo. Development and prospect of aeroengine dynamic pressure testing[J]. Technology Outlook, 2015(27): 144-145. [杨学广,张晓光,邢志国. 航空发动机动态压力测试发展与展望[J]. 科技展望, 2015(27): 144-145. DOI:10.3969/j.issn.1672-8289.2015.27.132] |
| [2] |
Kou Haijun,Zhang Junhong,Lin Jiewei. Aero-engine fan blade vibration characteristic analysis[J]. Journal of Xi’an Jiaotong University, 2014, 48(11): 109-114. [寇海军,张俊红,林杰威. 航空发动机风扇叶片振动特性分析[J]. 西安交通大学学报, 2014, 48(11): 109-114. DOI:10.7652/xjtuxb201411019] |
| [3] |
Huang Xiqiao,Yan Chuanjun,Wang Zhiwu,et al. Effect of operating frequency on performance of pulse detonation engine driven ejector[J]. Journal of Aerospace Power, 2008, 23(3): 401-405. [黄希桥,严传俊,王治武,等. 爆震频率对脉冲爆震发动机引射性能影响的实验[J]. 航空动力学报, 2008, 23(3): 401-405. DOI:10.13224/j.cnki.jasp.2008.03.025] |
| [4] |
Huang Xiqiao,Li Yang,Chen Le,et al. Experimental study on thrust augmentation of ejector driven by pulse detonation engine[J]. Journal of Northwestern Polytechnical University, 2013, 31(1): 55-59. [黄希桥,李洋,陈乐,等. 脉冲爆震发动机引射器增推性能的实验研究[J]. 西北工业大学学报, 2013, 31(1): 55-59. DOI:10.3969/j.issn.1000-2758.2013.01.011] |
| [5] |
Liu Hong,Xing Yongzhen,Xia Hua. Overpressure measurement and data analysis of muzzle shock wave[J]. Science & Technology Information, 2016, 14(1): 8-9. [刘红,邢永祯,夏华. 膛口冲击波超压测试及数据分析[J]. 科技资讯, 2016, 14(1): 8-9. DOI:10.16661/j.cnki.1672-3791.2016.01.008] |
| [6] |
Rahman Hebibul,Wang Hongyan,Xue Fangzheng,et al. High temperature dynamic pressure sensor and experimental analysis[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(2): 44-50. [热合曼·艾比布力,王鸿雁,薛方正,等. 耐高温动态压力传感器与实验分析研究[J]. 实验流体力学, 2017, 31(2): 44-50. DOI:10.11729/syltlx20170028] |
| [7] |
ISA.A guide for the dynamic calibration of pressure transducers:ISA–37.16.01—2002[S].North Carolina,2002.
|
| [8] |
Yang Fan,Kong Deren,Jiang Bo,et al. Dynamic characteristic of shock wave pressure sensor based on shock tube calibration[J]. Journal of Nanjing University of Science and Technology, 2017, 41(3): 330-336. [杨凡,孔德仁,姜波,等. 基于激波管校准的冲击波压力传感器动态特性研究[J]. 南京理工大学学报, 2017, 41(3): 330-336. DOI:10.14177/j.cnki.32-1397n.2017.41.03.009] |
| [9] |
Yang Jun,Shi Bo,Fan Shangchun,et al. Liquid high pulse pressure calibration by laser interferometry[J]. Explosion and Shock Waves, 2018, 38(3): 572-578. [杨军,史博,樊尚春,等. 基于激光干涉测量的液体高脉冲压力校准[J]. 爆炸与冲击, 2018, 38(3): 572-578. DOI:10.11883/bzycj-2016-0280] |
| [10] |
Li Qiang,Wang Zhongyu,Wang Zhuoran. Uncertainty evaluation for the dynamic calibration of pressure transducer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 847-856. [李强,王中宇,王卓然. 压力传感器动态校准不确定度评定[J]. 北京航空航天大学学报, 2015, 41(5): 847-856. DOI:10.13700/j.bh.1001-5965.2014.0356] |
| [11] |
Li Bo,Yang Jun,Huang Nan,et al. Dynamic calibration technology for measuring sinusoidal pressure of water medium based on laser interferometry[J]. Infrared and Laser Engineering, 2019, 48(8): 18-24. [李博,杨军,黄楠,等. 基于激光干涉法测水介质正弦压力的动态校准技术[J]. 红外与激光工程, 2019, 48(8): 18-24. DOI:10.3788/IRLA201948.0805003] |
| [12] |
Huang Chengzhi.Development of piezoelectric stack pumpand hydraulic linear actuator[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2013. 黄成志.压电叠堆泵及直线驱动器设计[D].南京:南京航空航天大学,2013. |
| [13] |
Xu Weihua,Bao Hai,Yang Yihan,et al. Voltage signal transmission principle based on the inverse piezoelectric effect of piezoelectric ceramic[J]. Automation of Electric Power Systems, 2010, 34(4): 80-83. [许韦华,鲍海,杨以涵,等. 基于压电陶瓷逆压电效应的电压信号变送原理[J]. 电力系统自动化, 2010, 34(4): 80-83.] |
| [14] |
Wang Zhaoqiang,Liu Haili,Xu Tianzhu,et al. Efficient energy conversion structure of a piezoelectric stack oscillator[J]. Journal of Vibration and Shock, 2011, 30(12): 125-128. [王兆强,刘海利,徐天柱,等. 谐振式压电叠堆的高效换能结构研究[J]. 振动与冲击, 2011, 30(12): 125-128. DOI:10.3969/j.issn.1000-3835.2011.12.025] |
| [15] |
Khodier S A. Refractive index of standard oils as a function of wavelength and temperature[J]. Optics & Laser Technology, 2002, 34(2): 125-128. DOI:10.1016/s0030-3992(01)00101-3 |
| [16] |
Wagner W. The IAPWS Industrial Formulation 1997 for the thermodynamic properties of water and steam[J]. Trans Asme Journal of Engineering for Gas Turbine & Power, 2000, 122(1): 150-184. DOI:10.1007/978-3-662-03529-0_3 |
 2020, Vol. 52
2020, Vol. 52

