高速逆流色谱技术HSCCC是一种连续的液–液萃取分离技术,通过在两个不混溶液相之间反复分配溶质来实现分离[1]。HSCCC具有适用范围广、无污染、高效和分离量大等优点,并广泛应用于生物医学、食品、天然产物、有机合成等多个领域。在色谱柱内,其中一个液相作为固定相,通过行星运动中分离柱内产生的流体动力平衡而保持静止,而另一个作为流动相,通过高压泵连续不断地输入到管路中,用作溶质载体。色谱柱的每一圈螺旋管内存在着一个混合区与一个分层区,并且沿着管的长度方向是连续存在的,这种交替的过程对色谱分离尤其重要。例如在1 200 r/min转速下,注入流动相的样品可以在1秒钟内经历20次重复混合和分层过程,由于不同物质在互不相溶的两相溶剂中的分配系数不同,分配系数的大小影响洗脱时间的长短,分配系数越小就越早洗脱,所以高速逆流色谱能够实现高效分配[2]。
自逆流色谱仪被发明以来,Ito等[1-2],曹学丽[3]开发了一系列逆流色谱装置,常见的逆流色谱仪类型有I型和J型,由于J型CCC装置设计巧妙、分离效果好,所以在实验室与商业上得到了较广泛的运用。J型逆流色谱为平行轴同步行星式运动色谱,主要由装置结构和分离柱结构组成,分离柱安装在行星架上,当分离柱绕公转轴公转的同时,也会绕自转轴同向高速自转。所以它既有自转又有公转。这种行星传动有很多优点:结构紧凑,承载能力大;传动效率高;运动平稳、抗冲击和振动能力较强。
目前,国内对逆流色谱仪器系统研发较少,且色谱仪多为分析型。李振帅等[4]对分析型高速逆流色谱的中心轴进行了动静态性能研究。陈箭峰等[5]对大容量高速逆流色谱的关键核心零件分离柱设计与性能进行了相关研究。作者将在此基础上设计J型大容量高速逆流色谱仪行星架。行星架是让分离柱稳定工作的重要部件,所以保证行星架的刚度、强度以及稳定性非常重要,通过有限元方法对其进行静强度分析和模态分析,并使用HyperWorks的拓扑优化功能,对行星架进行结构优化。
1 色谱仪机械传动系统色谱仪主体结构如图1所示,其机械传动系统主要包括行星架、分离柱、V型皮带、双面齿同步带、中心轴、行星轴、电机、同步带轮、V型带轮。左右中心轴通过轴承与机架装配,行星架通过两边中心轴安放在水平中央位置,两个质量一样的分离柱对称地装在行星架的两边,在每个分离柱的行星左轴上都装有1个同步带轮,它们与固定的中心同步带轮通过双面齿同步带相啮合,这3个同步带轮的尺寸和齿数是一样的[3];分离柱内部螺旋软管的端口通过小通管引出,与外面的输液泵、检测器相连接。
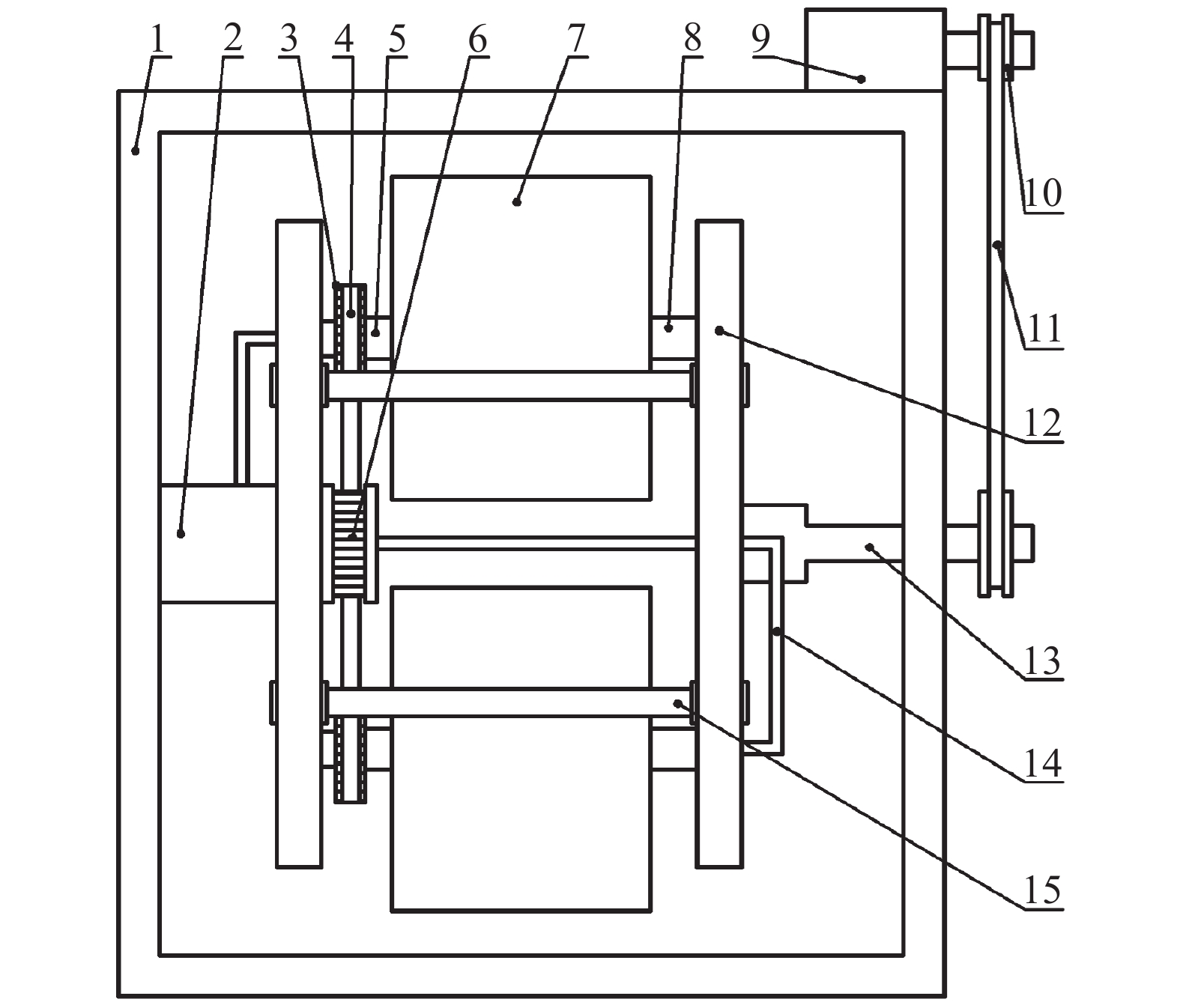 |
| 1.机架;2.中心左轴;3.行星同步带轮;4.双面齿同步带;5.行星左轴;6.中心同步带轮;7.分离柱;8.行星右轴;9.电机;10.V型带轮;11.V型皮带;12.行星架;13.中心右轴;14.小通管;15.钢管。 图1 色谱仪主体结构 Fig. 1 Main structure of chromatograph |
工作原理:电机通过V型皮带带动行星架旋转,则行星架上的分离柱绕中心轴进行公转,同时分离柱自身也会绕行星轴进行自转,从而色谱仪在公转与自转运动中产生了关键的离心合力场。当分离柱获得高速转速时,便能得到快速、制备量大的分离效果。
通过对色谱文献[6-7]的研究,得知
| 表1 行星结构的主要参数 Tab. 1 Main parameters of planetary structure |
 |
2 行星结构的静力分析 2.1 建立有限元模型
采用SolidWorks建立行星结构的3维模型,并对一些小特征进行简化,能有效得到收敛计算结果。根据实际工作情况,选择行星板材料为超硬铝7075,钢管选用结构钢Q235,材料属性如表2所示。将简化的有限元模型导入HyperMesh中,检查模型的边、面缺陷,进行几何清理;为保证网格质量,先进行2D网格划分,再划分3D网格,行星板的单元尺寸选择4 mm,钢管的单元尺寸选择2 mm,最后生成四面体单元,并检查网格质量。模型网络划分的结果如图2所示。
| 表2 材料属性 Tab. 2 Material properties |
 |
 |
| 图2 网格划分的行星架有限元模型 Fig. 2 Finite element model of planet carrier with mesh generation |
2.2 施加约束和载荷
两侧的行星板通过4个螺栓孔与4根钢管相连接,在HyperMesh中,在螺栓孔周围将所有的节点使用RBE2单元连接,以模拟螺栓连接;在中心左轴与行星板接触的地方施加位移约束,行星架主要受扭矩、分离柱的公转离心力和组件重力的作用。所选电机的功率为1.5 kW,额定转速为2 850 r/min,通过设计电机轴上的V型带轮与中心V型带轮的大小,使其传动比为2∶1,当中心右轴获得的转速为1 425 r/min,算得中心右轴的扭矩为10.1 Nm。则此时行星架角速度为149.2 rad/s,且每个分离柱的质量为9 kg,使用式(1)可计算公转离心力。
| $F = Ma = M{\omega ^2}R$ | (1) |
式中:F为分离柱的公转离心力,N;M为分离柱质量,kg;
计算得到每个分离柱所受的公转离心力为24 442 N。且行星架上的组件总质量为22 kg,其重力为216 N。把受力施加在行星架上,行星架的约束与载荷加载如图3所示。
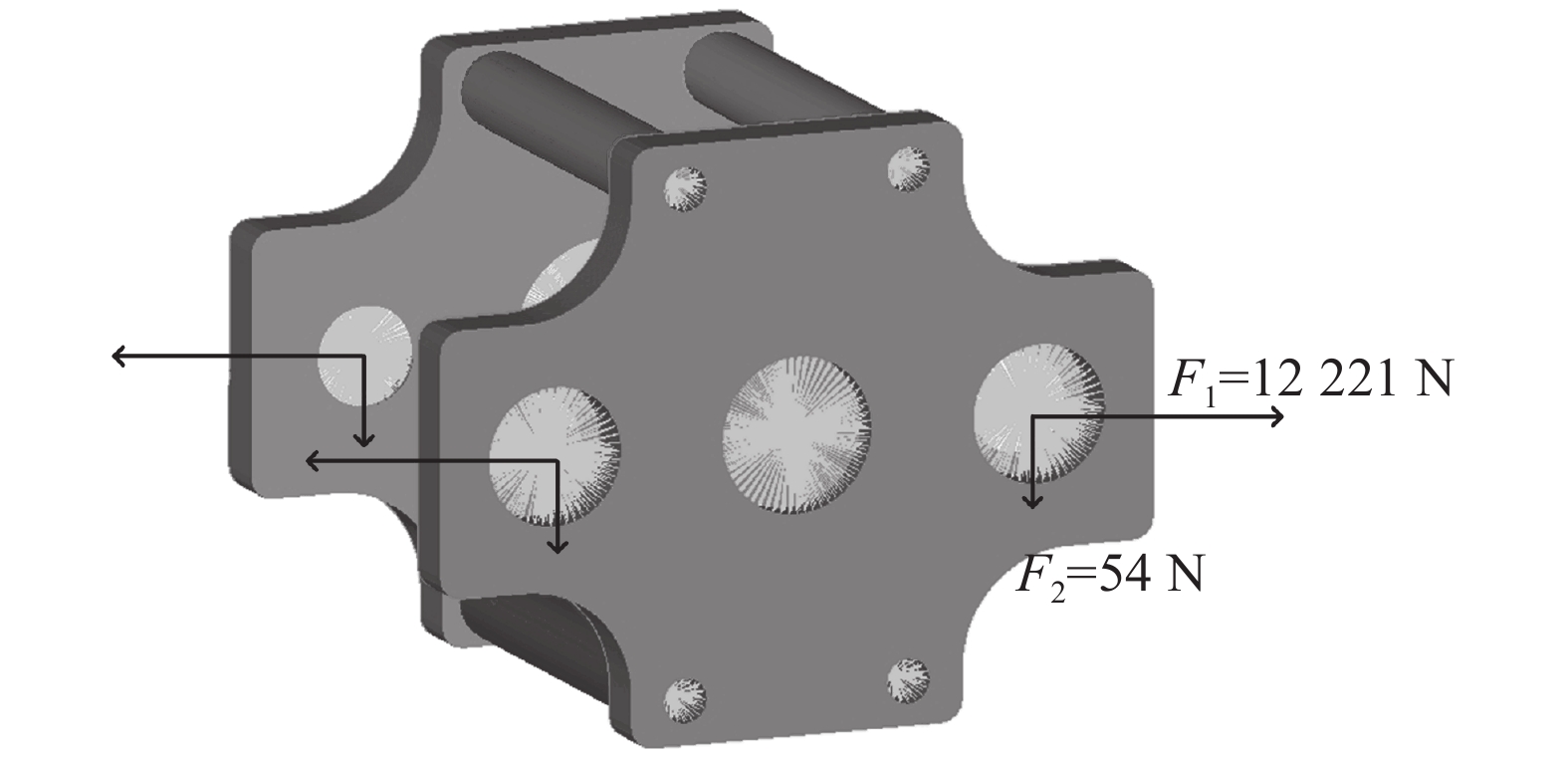 |
| 图3 约束与载荷 Fig. 3 Constraints and loads |
图3中,F1由24442 N在分离柱的一对安装孔上均分而得,F2由216 N在4个分离柱安装孔上均分而得。水平方向的力施加为F1,竖直方向的力施加为F2,每个分离柱安装孔均施加相同的F1和F2。各螺栓孔周围所有的节点使用RBE2单元连接。
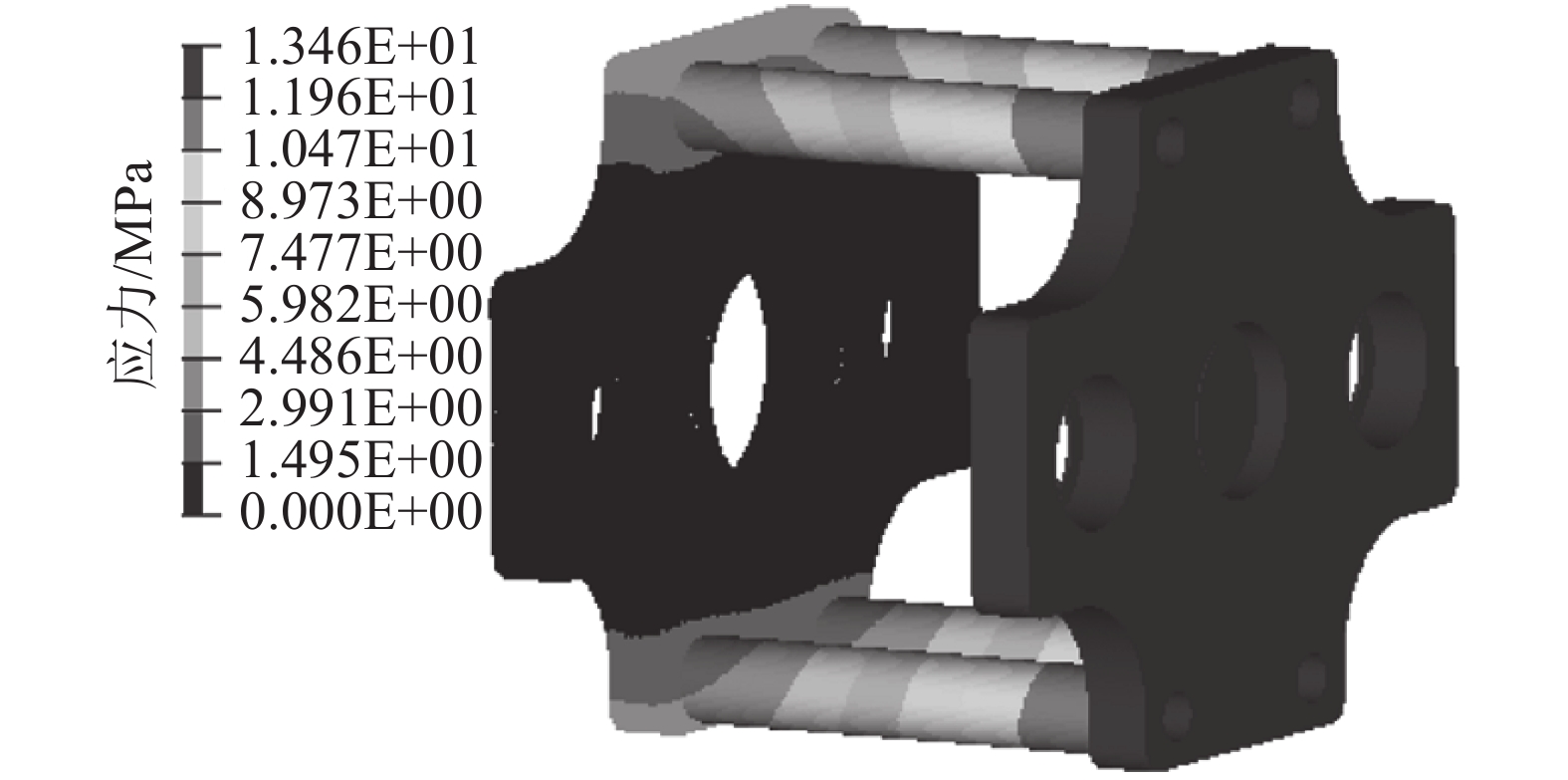
2.3 静力分析通过上述的加载约束,求得行星架的变形和应力情况[8],如图4所示。从图4(a)可得,行星架的最大变形为0.010 mm,发生在行星板的边缘处;从图4(b)可得,行星架的最大等效应力为10.74 MPa,由表2知7075的抗拉强度为560 MPa,故强度远远满足要求。结果分析表明:行星架的结构还可以进一步优化,以得到更优的模型。
 |
| 图4 行星架静力分析结果 Fig. 4 Static analysis results of planet carrier |
3 模态分析
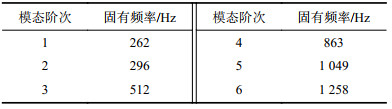
模态分析是整个动力学分析的基础,通过模态分析可识别出结构的固有频率与振型,对行星架进行约束模态分析。求解得到其前6阶固有频率[9],如表3所示。行星架的1阶振型如图5所示。
| 表3 行星架的固有频率 Tab. 3 Natural frequency of planet carrier |
 |
 |
| 图5 行星架的1阶振型 Fig. 5 First-order mode of planet carrier |
由表3可知,行星架各阶模态下的固有频率随模态阶次的升高而逐渐增大,在机构正常工作过程中,行星架的最高转速为1 425 r/min,可知它转动时最高激振频率为23.75 Hz,而行星架1阶固有频率高达262 Hz,远大于分离柱工作时的最高激振频率,所以发生共振的可能性很小。
4 行星架拓扑优化拓扑优化技术是一种广泛应用的结构优化设计方法,能够在给定的设计空间内寻求最佳的材料分布,以此得到优化结构的良好性能[10]。OptiStruct拓扑优化的材料模式采用SIMP法,假定材料的材料弹性模量与密度有关,将设计空间每个单元的“Density”作为设计变量,0~1之间连续取值,通过引惩罚因子对中间密度值进行惩罚,使中间密度向0~1两端聚集,这样就将拓扑优化问题转化为单元材料密度的最优分布问题。图6为基于HyperWorks的行星架结构优化流程图。
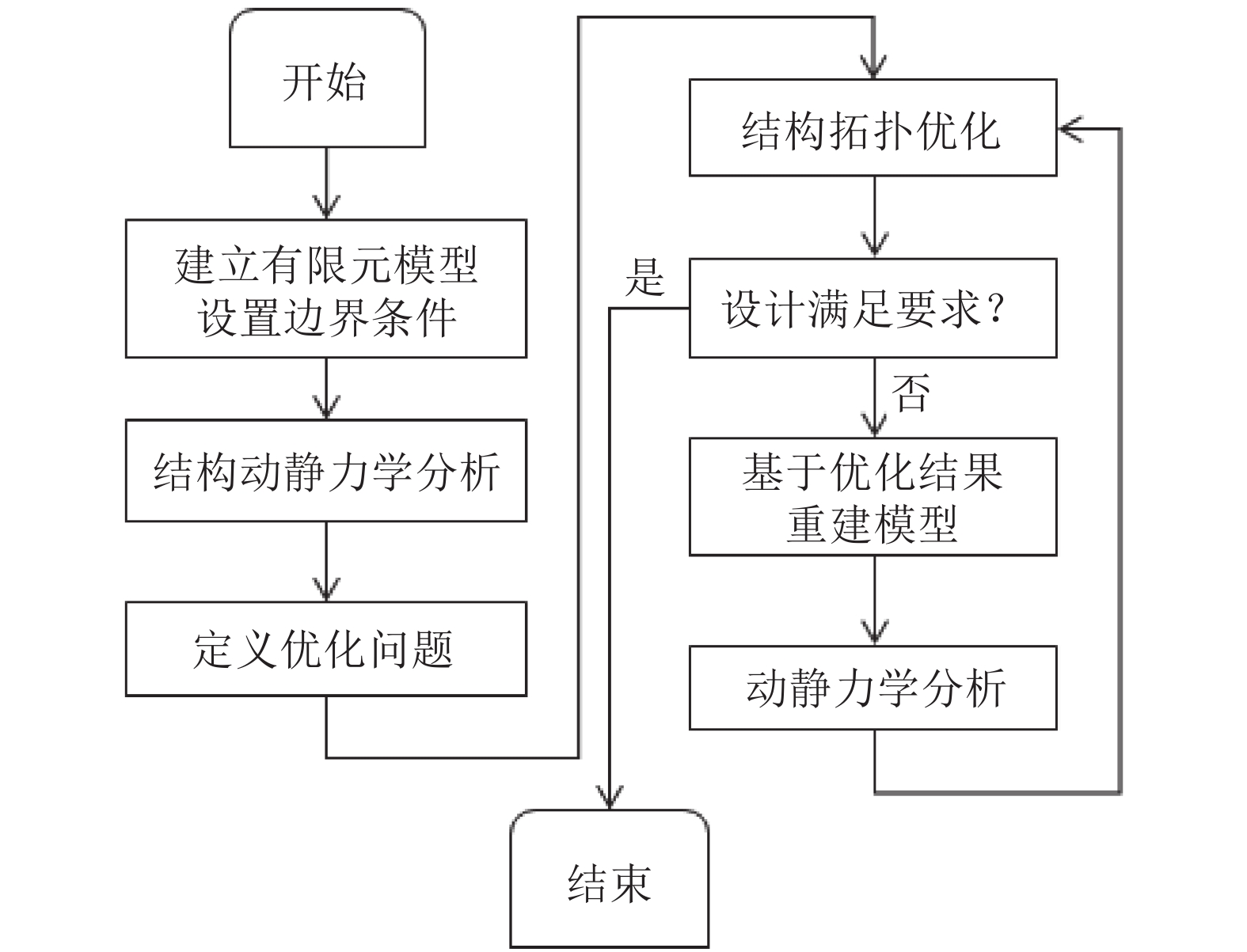 |
| 图6 拓扑优化流程 Fig. 6 Topology optimization process |
4.1 确定拓扑优化数学模型
提高低阶固有频率能改善模态特性,减小共振概率。考虑结构柔度是为了提高刚度,柔度越小则刚度越大,柔度是用单元应变能来定义的。所以综合考虑提高低阶固有频率和最小化柔度的多目标优化,能提高行星架整体的动静态性能。能实现这种目标可采用折衷规划法[11],其思想是多目标问题转化为求解Euclidean距离最小,从而得到多目标函数的折衷解(即全局最优值),此时单目标能获得较优值。则行星架多目标拓扑优化数学模型为[12]:
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \min F(\rho ) = \left\{ {{\varphi ^2}{{\left( {\displaystyle\sum\limits_{k = 1}^m {{w_k}} \frac{{{C_k}(\rho ) - C_k^{\min }}}{{C_k^{\max} - C_k^{\min}}}} \right)}^2} + } \right.\\ {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\left( {1 - \varphi } \right)}^2}{{\left( {\displaystyle\sum\limits_{j = 1}^n {{w_j}} \frac{{\lambda _j^{\max} - {\lambda _j}\left( \rho \right)}}{{\lambda _j^{\max} - \lambda _j^{\min }}}} \right)}^2}} \right\}^{1/2},} \end{array}\\ {\begin{array}{*{20}{l}} {{\rm{ find }}\rho (x)},\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}V(\rho )/{V_0} \le \eta {\text{。}}} \end{array}} \end{array}} \right. $ |
式中,
在第2、3节动静力学的基础上,再进行单目标拓扑优化[13],优化设计主要包含3个要素:设计变量、设计约束和设计目标。在优化前先要将结构划分出设计区域和非设计区域,根据行星结构的特点以及外观要求,将行星板划分为设计区域,其余为非设计区域。第1个单目标优化对象是前两阶频率,约束条件为优化设计区域体积分数上限为0.3,设计目标为频率最大,优化结果如图7所示,第1阶和第2阶优化频率分别为343、421 Hz。第2单目标优化对象是柔度,约束条件为体积分数上限为0.3,设计目标为柔度最小,优化结果如图8所示,柔度由733 N·mm下降至最小值99 N·mm。
 |
| 图7 单目标频率优化 Fig. 7 Single objective frequency optimization |
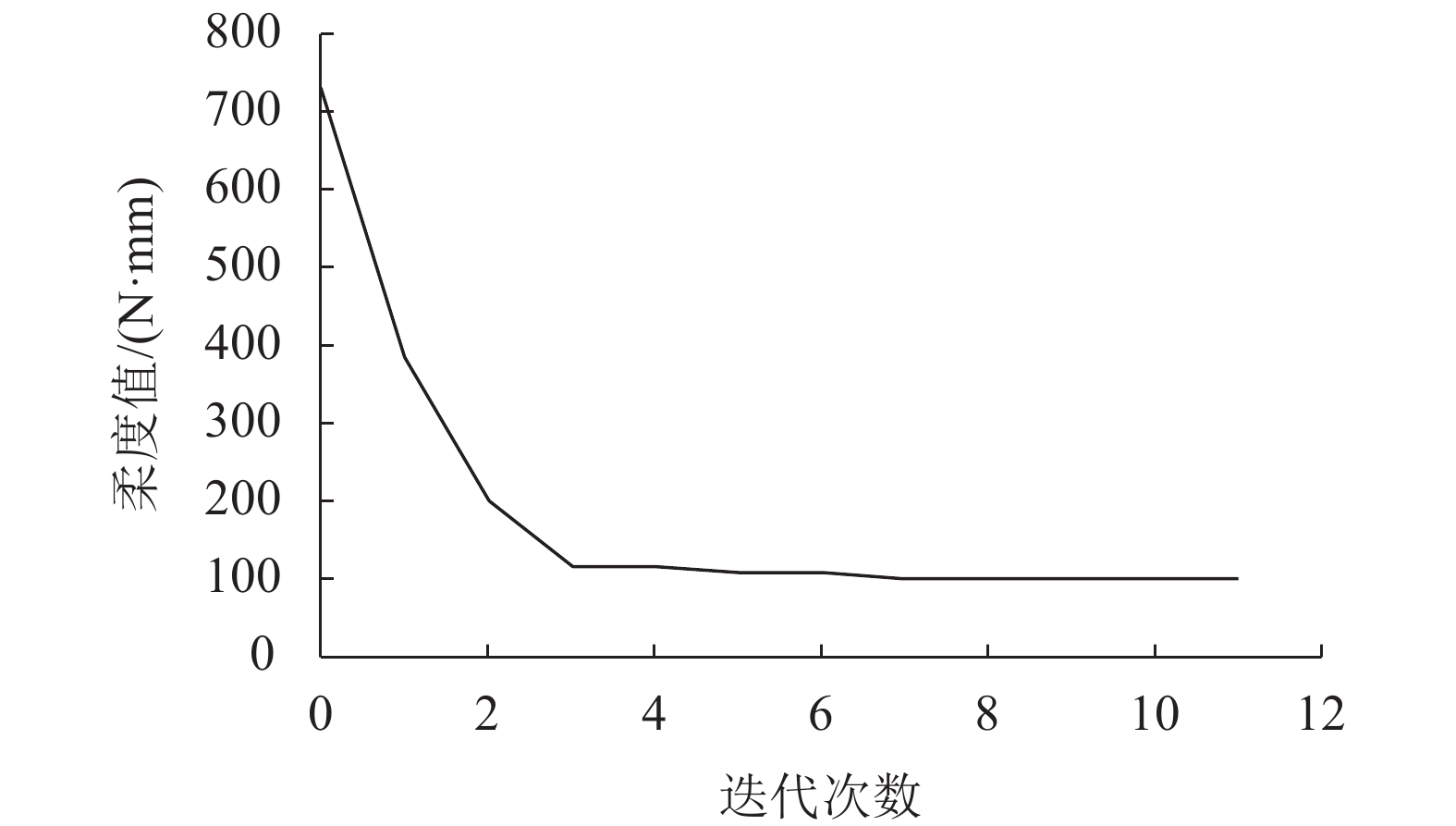 |
| 图8 单目标柔度优化 Fig. 8 Single objective flexibility optimization |
4.3 多目标拓扑优化
经静力学分析,得出最大变形量较小,所以设置柔度权重为0.35,频率总权重为0.65,因第1阶频率比第2阶频率稍重要,设置第1、2阶频率权重分别为0.6与0.4;利用单目标优化数据,设置多目标函数为:
| $ \begin{aligned}[b] f(x) =& {\rm{rss}} \left( {0.35 \times \left( {{x_1} - 99} \right)/634,0.39 \times \left( {343 - {x_2}} \right)/} \right.\\ &\left. {217,0.26 \times \left( {421 - {x_3}} \right)/268} \right){\text{。}} \end{aligned} $ |
式中,
再进行多目标拓扑优化分析[14-15],约束为不超过优化设计区域体积分数0.3,目标为使带权重系数的多目标函数最小化,经过20次迭代后收敛,结果如图9所示。目标函数值为归一化的Euclidean距离,其迭代收敛过程如图9(a)所示,目标函数由0.58最终收敛到0.1;频率和柔度优化结果如图9(b)和(c)所示,最后第1阶频率稳定在307 Hz。第2阶频率稳定在367 Hz,柔度降到了215 N·mm。
 |
| 图9 多目标函数优化 Fig. 9 Multi-objective function optimization |
4.4 优化结果
图10描述的是拓扑优化结果,灰度浅部分表示该单元体的密度接近0,灰度深部分表示该单元体的密度接近1;当取单元密度阈值为0.25时,即去除密度云值低于0.25的区域,可以很清楚显示行星架的主体轮廓。
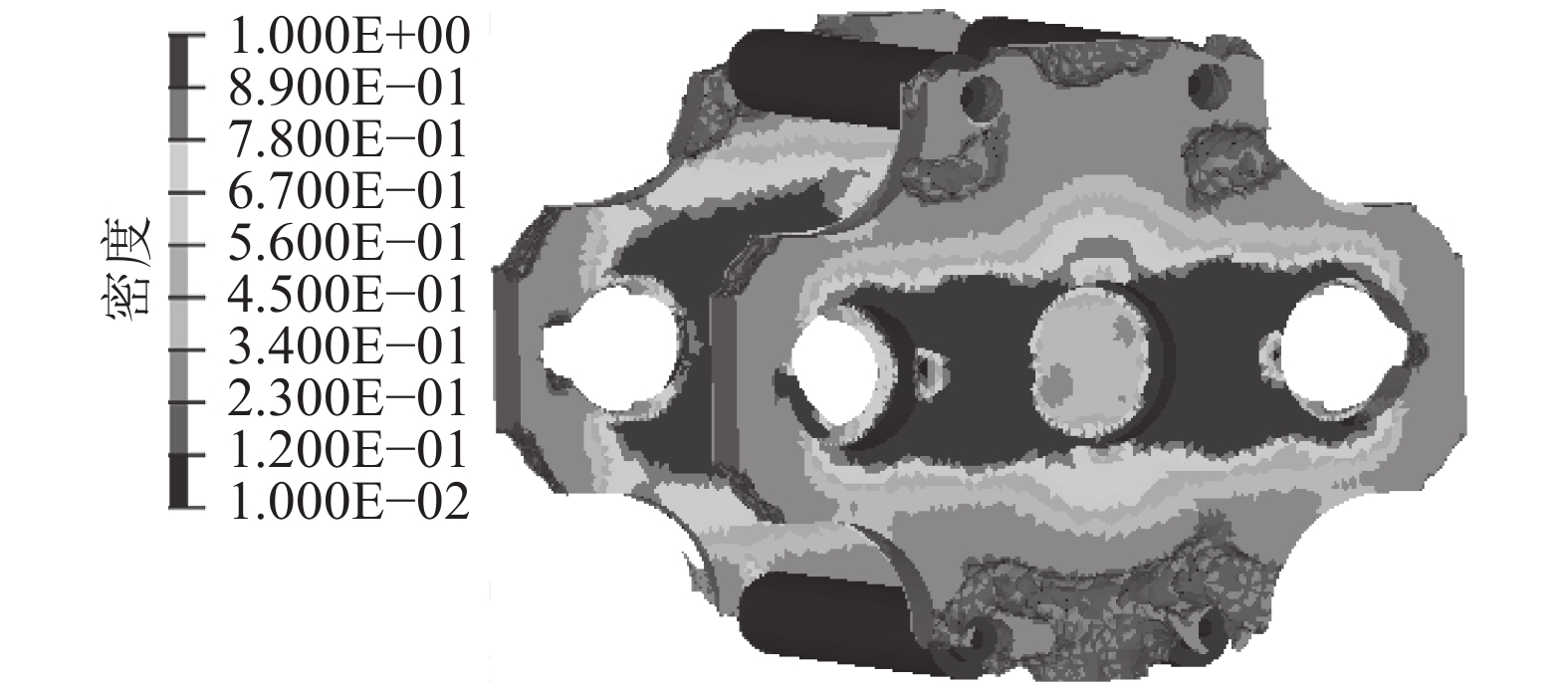 |
| 图10 拓扑优化结果 Fig. 10 Result of topology optimization |
4.5 二次建模及静力学分析
基于拓扑优化所得到的结果,将优化结果与制造工艺要求相结合,对行星架进行重新设计,在设计过程中进行一定的调整。基于以下原则:在SolidWorks中重建实体模型,新模型如图11所示。
 |
| 图11 行星架的新模型 Fig. 11 New model of planet carrier |
1)保持优化后结构的轮廓,灰度浅部分区域可合理去除;
2)考虑易加工性原则,用规则平面和圆滑曲面替换不规则面;
3)在受力较小区域可适当加沉槽。
得到新模型,将优化后的行星架赋予材料属性,得到其质量为6.85 kg;将模型导入到HyperWorks中,约束和载荷与前文相同,再求解计算,观察其变形和应力情况。优化后行星架的变形和应力云图如图12所示。
 |
| 图12 新模型的变形与应力 Fig. 12 Deformation and stress of new model |
从图12中可知,优化后的行星架最大应力为7.95 MPa,最大变形量为0.013 mm,其强度和刚度都能满足要求。
性能数值对比如表4所示。从表4得知:与初始行星架相比,优化后的行星架质量减轻了1.03 kg,降低了13.1%,达到了轻量化的优化目标;最大应力降低到7.95 MPa,减少了26%;最大变形虽然有点微增,小于本设计允许变形量0.03 mm,满足静力学要求。
| 表4 优化前后的数值对比 Tab. 4 Numerical comparison before and after optimization |
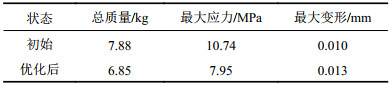 |
5 结 论
设计了一种高速逆流色谱仪行星架结构,并利用HyperWorks软件对其进行了动静态性能研究和拓扑优化,最后对优化后的模型再进行验证。得到以下结论:
1)对行星架进行了有限元静力学分析和模态分析,得到了行星架主体的变形和应力情况,以及前6阶模态参数。对这些特性进行了评估,得到动静力学基本满足要求。
2)为避免单目标拓扑优化的缺陷,因此对模型进行了多目标优化,从而保证一定的刚度和模态性能条件;再根据优化模型重新设计,通过有限元分析的对比,优化后行星架的整体性能有了一定的提升,质量也得到了减轻。结果显示得到了一个材料分布更优、性能更好的行星架结构。
| [1] |
Ito Y,Bowman R L. Countercurrent chromatography:Liquid-liquid partition chromatography without solid support[J]. Science, 1970, 167(3916): 281-283. DOI:10.1126/science.167.3916.281 |
| [2] |
Ito Y. Golden rules and pitfalls in selecting optimum conditions for high-speed counter-current chromatography[J]. Journal of Chromatography(A), 2005, 1065(2): 145-168. DOI:10.1016/j.chroma.2004.12.044 |
| [3] |
曹学丽.高速逆流色谱分离技术及应用[M].北京:化学工业出版社,2005.
|
| [4] |
Li Zhenshuai,Chen Haijun,Yin Qin,et al. Dynamic and static performance analysis of the central axis transmission system of HSCCC[J]. Journal of Xi hua University(Natural Science Edition), 2019, 38(3): 26-31. [李振帅,陈海军,殷勤,等. 高速逆流色谱仪中心轴传动系统动静态性能分析[J]. 西华大学学报(自然科学版), 2019, 38(3): 26-31. DOI:10.3969/j.issn.1673-159X.2019.03.005] |
| [5] |
Chen Jianfeng,Chen Haijun,Yin Qin,et al. Structure design and optimization of large-capacity high-speed countercurrent chromatography separation column[J]. China Measurement &Test, 2019, 45(5): 98-104. [陈箭峰,陈海军,殷勤,等. 大容量高速逆流色谱仪分离柱结构设计与优化[J]. 中国测试, 2019, 45(5): 98-104. DOI:10.11857/j.issn.1674-5124.2018070115] |
| [6] |
Guan Y H,Heuvel R V D. The three dimensional model for helical columns on type-J synchronous counter-current chromatography[J]. Journal of Chromatography(A), 2011, 1218: 5108-5114. DOI:10.1016/j.chroma.2011.05.078 |
| [7] |
Guzlek H,Baptista I I R,Wood P L,et al. A novel approach to modeling counter-current chromatography[J]. Journal of Chromatography(A), 2010, 1217: 6230-6240. DOI:10.1016/j.chroma.2010.08.011 |
| [8] |
Zang Xiaolei,Gu Zhengqi,Mi Chengji,et al. Static/dynamic multi-objective topology optimization of the frame structure in a mining truck[J]. Automotive Engineering, 2015, 37(5): 566-570. [臧晓蕾,谷正气,米承继,等. 矿用车车架结构的静动态多目标拓扑优化[J]. 汽车工程, 2015, 37(5): 566-570. DOI:10.19562/j.chinasae.qcgc.2015.05.015] |
| [9] |
Li Meng,Yin Guofu,Fang Hui,et al. Modal analysis of HSCCC planetary carrier based on ANSYS workbench[J]. Manufacturing Automation, 2015, 37(12): 8-10. [李猛,殷国富,方辉,等. 基于ANSYS Workbench的高速逆流色谱仪行星架模态分析[J]. 制造业自动化, 2015, 37(12): 8-10. DOI:10.3969/j.issn.1009-0134.2015.06.03] |
| [10] |
洪清泉,赵康,张攀,等.OptiStruct & HyperStudy理论基础与工程应用[M].北京:机械工业出版社,2012.
|
| [11] |
Liu Linhua,Xin Yong,Wang Wei.Multi-objective topology optimization for an off-road vehicle frame based on compromise programming[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(3):382-385. 刘林华,辛勇,汪伟.基于折衷规划的车架结构多目标拓扑优化设计[J].机械科学与技术,2011,30(3):382-385. |
| [12] |
Zhang Zhifei,Chen Ren,Xu Zhongming,et al. Research on multi-objective topology optimization of vehicle suspension control arm[J]. Journal of Mechanical Engineering, 2017, 53(4): 114-121. [张志飞,陈仁,徐中明,等. 面向多目标的汽车悬架控制臂拓扑优化研究[J]. 机械工程学报, 2017, 53(4): 114-121. DOI:10.3901/JME.2017.04.114] |
| [13] |
Lan Fengchong,Lai Fanjie,Chen Jiqing,et al. Multi-case topology optimization of body structure considering dynamic characteristic[J]. Journal of Mechanical Engineering, 2014, 50(20): 122-128. [兰凤崇,赖番结,陈吉清,等. 考虑动态特性的多工况车身结构拓扑优化研究[J]. 机械工程学报, 2014, 50(20): 122-128. DOI:10.3901/JME.2014.20.122] |
| [14] |
Peng Ji,Tan Feng,Wei Yabin,et al. Dynamic-static topology optimization design method of fast reactor loader arm[J]. Advanced Engineering Sciences, 2017, 49(Supp2): 251-256. [彭骥,谭峰,卫亚斌,等. 快堆装载机支臂结构的动静态性能拓扑优化设计方法[J]. 工程科学与技术, 2017, 49(增刊2): 251-256. DOI:10.15961/j.Jsuese.201600941] |
| [15] |
Long Kai,Zuo Zhengxing,Yan Qingdong. Multi-objective optimization of continuum structures considering static and dynamic characteristic[J]. Journal of Astronautics, 2008, 29(2): 456-460. [龙凯,左正兴,闫清东. 静动态多目标下的连续体结构拓扑优化[J]. 宇航学报, 2008, 29(2): 456-460. DOI:10.16579/j.issn.1001.9669.2010.06.014] |
 2020, Vol. 52
2020, Vol. 52


