2. 网络与信息安全武警部队重点实验室,陕西 西安 710086;
3. 武警工程大学 教务处,陕西 西安 710086
2. Key Lab. of Network & Info. Security of PAP, Xi’an 710086, China;
3. Office of Academic Affairs, Eng. Univ. of PAP, Xi’an 710086, China
位置服务(location-based service,LBS)是一类在定位技术、地理信息系统和第三方位置服务提供商的支撑下,以用户位置信息为基础,向移动用户提供与位置相关的增值服务的总称[1-2]。近年来,LBS作为移动互联网中最重要的移动服务之一,正在全球以惊人的速度发展普及,呈现出井喷式发展态势。用户在享受更多位置服务的同时,也产生了大量位置数据信息,这些信息往往会明显或隐性地暴露用户的个人隐私信息,产生蝴蝶效应,引发更严重的个人隐私安全问题[3]。《Science》的“The end of privacy”[4]专题就曾指出,从用户的运动轨迹和位置信息,就能推理出其惯用路线、家庭工作单位地点、健康状况、生活习惯、兴趣爱好、社交关系、平时乘坐交通工具[5]等个人隐私信息。位置相关敏感信息的泄露已成为LBS中最大的隐私威胁,也给LBS在军用、民用领域的全方位普及带来了前所未有的挑战。然而,在当前移动社交网络中,LBS的应用几乎都离不开多方之间位置信息的实时共享[6],其中因共享导致的隐私泄露问题不容忽视。因此,如何在共享的同时实现对用户的位置隐私保护,已经成为研究者关注的热点和亟待解决的问题,深入研究符合网络特点和现实需求的LBS位置隐私保护技术具有广阔的应用前景和重要的现实意义。
传统的位置信息共享过程实行的是刚性的“全部或全不”隐私保护策略,无法满足用户的个性化、弹性位置隐私保护需求。为此,Marias等[7]最先提出将秘密共享技术用于位置信息的隐私保护,将用户位置信息利用随机数加密拆分成多个份额,并存放于多个STS(share the secret)服务器中,当用户发起位置服务时,位置服务器需要向每个STS服务器发出申请获得份额。虽然,该方案因引入额外的存储服务器会增加新的性能瓶颈与安全风险,也无法根据不同访问权限提供分级精度的位置共享结果,但是,其提出的多服务器秘密共享存储技术非常值得借鉴。Dürr等[8]借鉴多服务器存储的方法提出了在不可信系统中利用秘密共享策略实现位置共享隐私保护。该方案将系统假设为部分可信,基于坐标变换和空间模糊设计了位置秘密共享方法,分发有限精度的位置份额给多个位置服务器,不同精度的份额集合可重构出不同程度模糊的位置信息。但是,该方案有两个份额产生算法,较为复杂,多级别的位置信息需要多次共享,用户终端计算量较大。为了克服上述缺点,Skvortsov等[9]在开放的网络环境下,将精确位置模糊成具有不同半径的圆形区域,令攻击者从一定数量的份额中再难得到更加精确的位置信息。但是,该方案在较长时间内目标位置更新时生成的份额并不更新,仅适用于“签到”模式,且存储份额的服务器发生问题时,仍会泄露一定精度的目标位置信息。同时,Wernke等[10]提出了Pshare方案。该方案是第一个针对语义位置的多秘密共享隐私保护方案,解决了连续位置更新问题,增强了算法抵抗多种攻击的鲁棒性,并在后续研究中进行了优化和仿真[11-12]。然而,上述方案的计算量较大,当位置份额数量或参与存储份额的位置服务器增加时,其计算份额和重构位置的运算开销也会急剧增加,在移动互联网中资源受限的用户终端上并不适用。2017年,Skvortsov等[13]改变了之前文献[8-9, 11-12]方案中一直采用的“平等份额分发”模式,而预设服务器具有不同的可信级,可信度高的服务器能够存储更高精度的位置信息,反之亦然。但由于可信度高的服务器存储的是更高精度(更多数量)份额,该类服务器易变成攻击热点,且该方案直接采用一般概率信任模型[14]进行分级,需要额外维护管理一个服务器信任分级数据库。
综上所述,虽然LBS中位置共享隐私保护问题没有得到完美解决,但这些方案将位置信息转化为一系列份额分发给多个位置服务器以实现隐私保护的思想具有可借鉴性。作者针对多用户位置共享中的好友查找应用[15-16],基于弹性位置隐私保护策略,提出了一种能够满足用户个性化需求的分级位置共享隐私保护方案。本方案不需要引入其他服务器,也不依赖于位置服务器集的可信度,利用基于中国剩余定理的门限可变多秘密共享方法弹性地满足用户不同精度位置信息的共享需求。
1 方案描述 1.1 系统模型如图1所示,方案的系统模型主要由定位系统和位置隐私保护系统两部分组成。其中,位置隐私保护系统由查询目标
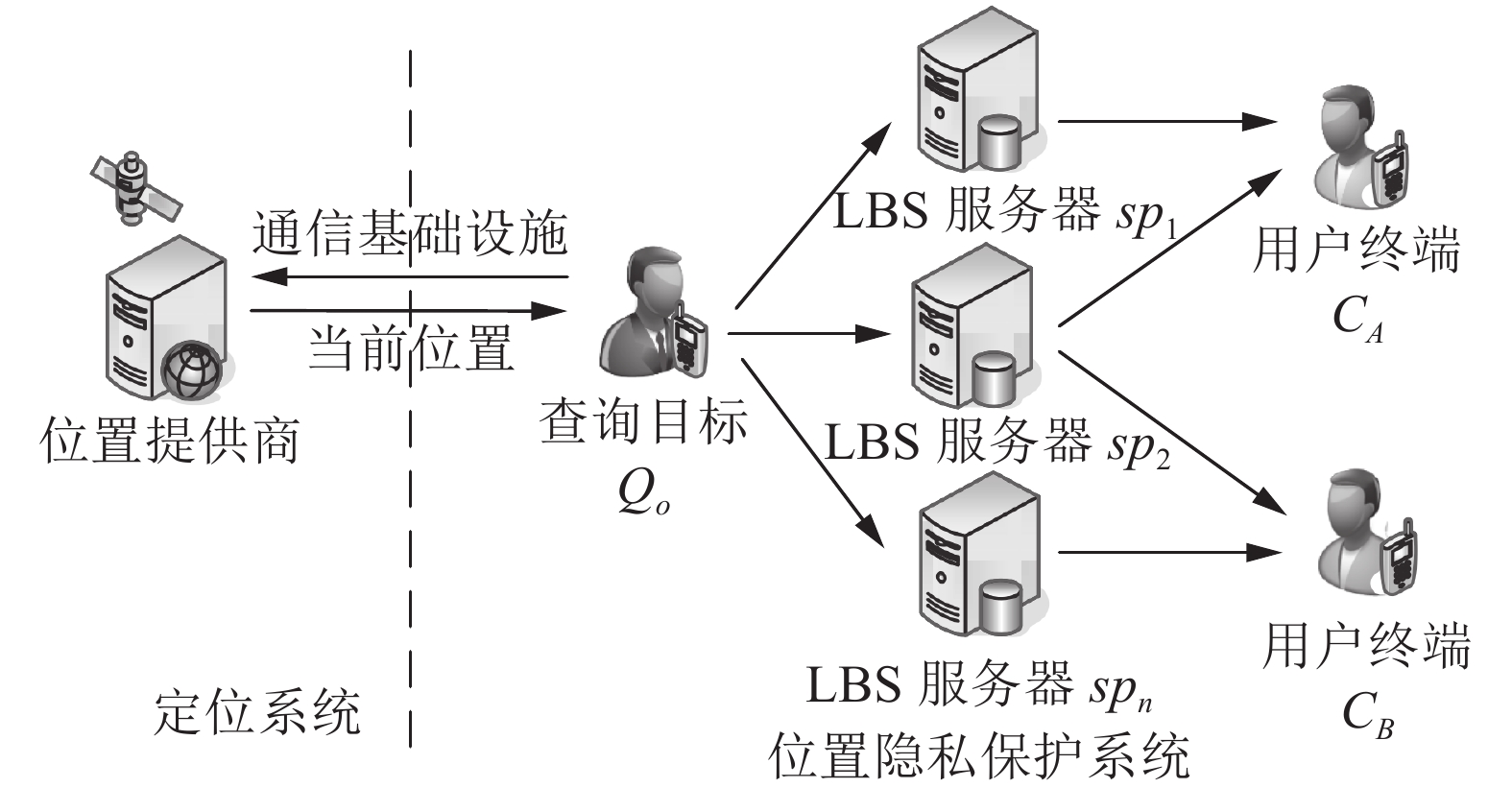 |
| 图1 多用户位置共享隐私保护模型 Fig. 1 Model of location sharing privacy protection for multi-users |
1.2 位置转换模型
用户通过两种位置转换模型可灵活地将真实位置坐标转换成不同精度的位置信息分级共享给其他用户,即自主把握共享位置的对象与精度级别,这更有利于满足实际网络环境中用户的个性化隐私需求。
1)地理位置转换模型
通常情况下,通过定位系统获得的位置经纬度坐标一般都以度(°)、分(′)、秒(″)表示,若用G表示查询目标的精确位置,则用户真实位置的地理坐标数字表示为
2)语义位置转换模型
根据通用规则,语义位置通常表示为{国家,省(州),市,区(县),乡/镇(街道),门牌号},可根据一定数字映射关系(规则)建立语义转换数据库,将语义位置对应表示为数字。如语义位置{中国,陕西省,西安市,未央区,三桥武警路,66号}对应的数字坐标可转换为{0086,71,00,86,0010,66}。精确位置的语义位置对应的数字坐标可表示为
本方案中位置信息共享机制将
1)查询目标选择
2)若
3)令
| $\left\{ \begin{array}{l} \left\{ \begin{array}{l} {a_0} \equiv {T_{1,1}}od {q_1},\\ {a_0} \equiv {T_{2,1}}od {q_2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ {a_0} \equiv {T_{{L_{\max }},1}}od {q_{{L_{\max }}}}; \end{array} \right.\left\{ \begin{array}{l} {a_1} \equiv {T_{1,2}}od {q_1},\\ {a_1} \equiv {T_{2,2}}od {q_2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ {a_1} \equiv {T_{{L_{\max }},2}}od {q_{{L_{\max }}}}; \end{array} \right.\\ \begin{array}{*{20}{l}} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\cdots \end{array}\\ \left\{ \begin{array}{l} {a_{{r_{{L_1}}} - 1}} \equiv {T_{1,{r_{{L_1}}}}}od {q_1},\\ {a_{{r_{{L_1}}} - 1}} \equiv {T_{2,{r_{{L_1}}}}}od {q_2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ {a_{{r_{{L_1}}} - 1}} \equiv {T_{{L_{\max }},{r_{{L_1}}}}}od {q_{{L_{\max }}}}; \end{array} \right.\left\{ \begin{array}{l} {a_{{r_{{L_1}}}}} \equiv 0od {q_1},\\ {a_{{r_{{L_1}}}}} \equiv {T_{2,{r_{{L_1}}} + 1}}od {q_2},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ {a_{{r_{{L_1}}}}} \equiv {T_{{L_{\max }},{r_{{L_1}}} + 1}}od {q_{{L_{\max }}}}; \end{array} \right.\\ \begin{array}{*{20}{l}} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\cdots \end{array}\\ \left\{ \begin{array}{l} {a_{{r_{{L_{\max }}}} - 1}} \equiv 0od {q_1},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ {a_{{r_{{L_{\max }}}} - 1}} \equiv 0od {q_{{L_{\max }} - 1}},\\ {a_{{r_{{L_{\max }}}} - 1}} \equiv {T_{{L_{\max }},{r_{{L_{\max }}}}}}od {q_{{L_{\max }}}}\end{array} \right. \end{array} \right.$ | (1) |
由中国剩余定理可求得式(1)的解
4)构造多项式。令
①若
设
| $ \begin{aligned}[b] F(x) =& {a_0} + {a_1}x + \cdots + {a_{{r_{_{{L_{\max }}}}} - 1}}{x^{{r_{{L_{\max }}}} - 1}} + \\ &{b_{{t_1}}}{x^{{r_{{L_{\max }}}}}} + \cdots + {b_{{t_{{L_{\max }}}} - 1}}{x^{{r_{{L_{\max }}}} + {t_{{L_{\max }}}} - {t_1} - 1}} \end{aligned} $ | (2) |
②若
| ${\;\;\;\;\;\;\;\;\;\;\;F(x)} = {a_0} + {a_1}x + \cdots + {a_{{t_{_{{L_{\max }}}}} - 1}}{x^{{t_{{L_{\max }}}} - 1}}$ | (3) |
5)计算
| $ {S_i} = F({x_i})od M $ | (4) |
6)若
| ${d_i} = F\left( i \right)od M$ | (5) |
7)将
假设用户
1)若
| ${\;\;\;\;\;\;\;\;\;\;\;{F_i}(x)} = F\left( x \right)od \;{q_i}\left( { \in {\mathbb{Z}_{{q_i}}}\left[ x \right]} \right)$ | (6) |
且满足
| $ {S_{i,j}} = {S_j}od \;{q_i} $ | (7) |
则用户得到
| $\left\{ {\begin{array}{*{20}{l}} {{{d}_1'} \equiv {d_1}od \;{q_i},} \\ {{{d}_2'} \equiv {d_2}od \;{q_i},} \\ \quad\quad\quad\vdots \\ {{{d}_{{r_{{L_{\max }}}} - t{}_1}'} \equiv {d_{{r_{{L_{\max }}}} - t{}_1}}od \;{q_i}} \end{array}} \right.$ | (8) |
则用户又可得到
| $ \begin{aligned}[b] {F_i}\left( x \right) &= F\left( x \right)od \;{q_i} = \\ &\;\;\left(\sum\limits_{j = 1}^{{t_i}} {\left( {{S_{i,j}}\prod\limits_{h = 1,h \ne j}^{{t_i}} {\frac{{x - {x_h}}}{{{x_j} - {x_h}}}} \prod\limits_{v = 1}^{{r_{{L_{\max }}}} - {t_1}} {\frac{{x - v}}{{{x_j} - v}}} } \right)} +\right. \\ &\left.\;\sum\limits_{j = 1}^{{r_{{L_{\max }}}} - {t_1}} {\left( {{{d}_j'}\prod\limits_{v = 1,v \ne j}^{{r_{{L_{\max }}}} - {t_1}} {\frac{{x - v}}{{j - v}}} \prod\limits_{h = 1}^{{t_i}} {\frac{{x - {x_h}}}{{j - {x_h}}}} } \right)}\right)od \;{q_i} = \\ &\;\;\;\;\;\;\;{a_0} + {a_1}x + \cdots + {a_{{r_{{L_{\max }}}} - 1}}{x^{{r_{{L_{\max }}}} - 1}} + \\ &\;{b_{{t_1}}}{x^{{r_{{L_{\max }}}}}} + \cdots + {b_{{t_{{L_{\max }}}} - 1}}{x^{{r_{{L_{\max }}}} + {t_{{L_{\max }}}} - {t_1} - 1}}od \;{q_i} = \\ &\;\;\;\;\;\;\;{a_0} + {a_1}x + \cdots + {a_{{r_{{L_{\max }}}} - 1}}{x^{{r_{{L_{\max }}}} - 1}} + \\ &\;\;\;\;\;\;\;{b_{{t_1}}}{x^{{r_{{L_{\max }}}}}} + \cdots + {b_{{t_i} - 1}}{x^{{r_{{L_{\max }}}} + {t_i} - {t_1} - 1}}od \;{q_i}\\[-10pt] \end{aligned} $ | (9) |
由
| $\left\{ \begin{array}{l} {T_{{L_i},1}} = {a_0}od \;{q_i}, \\ {T_{{L_i},2}} = {a_1}od \;{q_i}, \\ \quad\quad\quad\vdots \\ {T_{{L_i},{r_{{L_i}}}}} = {a_{{r_{{L_i}}} - 1}}od \;{q_i} \\ \end{array} \right.$ | (10) |
2)若
| ${\;\;\;\;\;\;\;\;\;\;\;\;{F_i}\left( x \right)} = F\left( x \right)od \;{q_i}\left( { \in {\mathbb{Z}_{{q_i}}}[x]} \right)$ | (11) |
且满足
| $ {S_{i,j}} = {S_j}od \;{q_i} $ | (12) |
则用户可得到
| $\begin{aligned}[b] {F_i}\left( x \right) &= F\left( x \right)od \;{q_i} = \\ &\;\;\;\;\;\;\;\sum\limits_{j = 1}^{{t_i}} {\left( {{S_{i,j}}\prod\limits_{h = 1,h \ne j}^{{t_i}} {\frac{{x - {x_h}}}{{{x_j} - {x_h}}}} } \right)} od \;{q_i} = \\ &\;\;\;\;{a_0} + {a_1}x + \cdots + {a_{{t_{{L_{\max }}}} - 1}}{x^{{t_{{L_{\max }}}} - 1}}od \;{q_i} = \\ &\;\;\;\;\;\;\;{a_0} + {a_1}x + \cdots + {a_{{r_{{L_i}}} - 1}}{x^{{r_{{L_i}}} - 1}} + \\ &\;\;\;\;\;{a_{{r_{{L_{\max }}}}}}{x^{{r_{{L_{\max }}}}}} + \cdots + {a_{{t_i} - 1}}{x^{{t_i} - 1}}od \;{q_i} \end{aligned} $ | (13) |
利用式(10)计算得出
作者设计的多用户位置共享分级隐私保护方案的执行过程如图2所示。
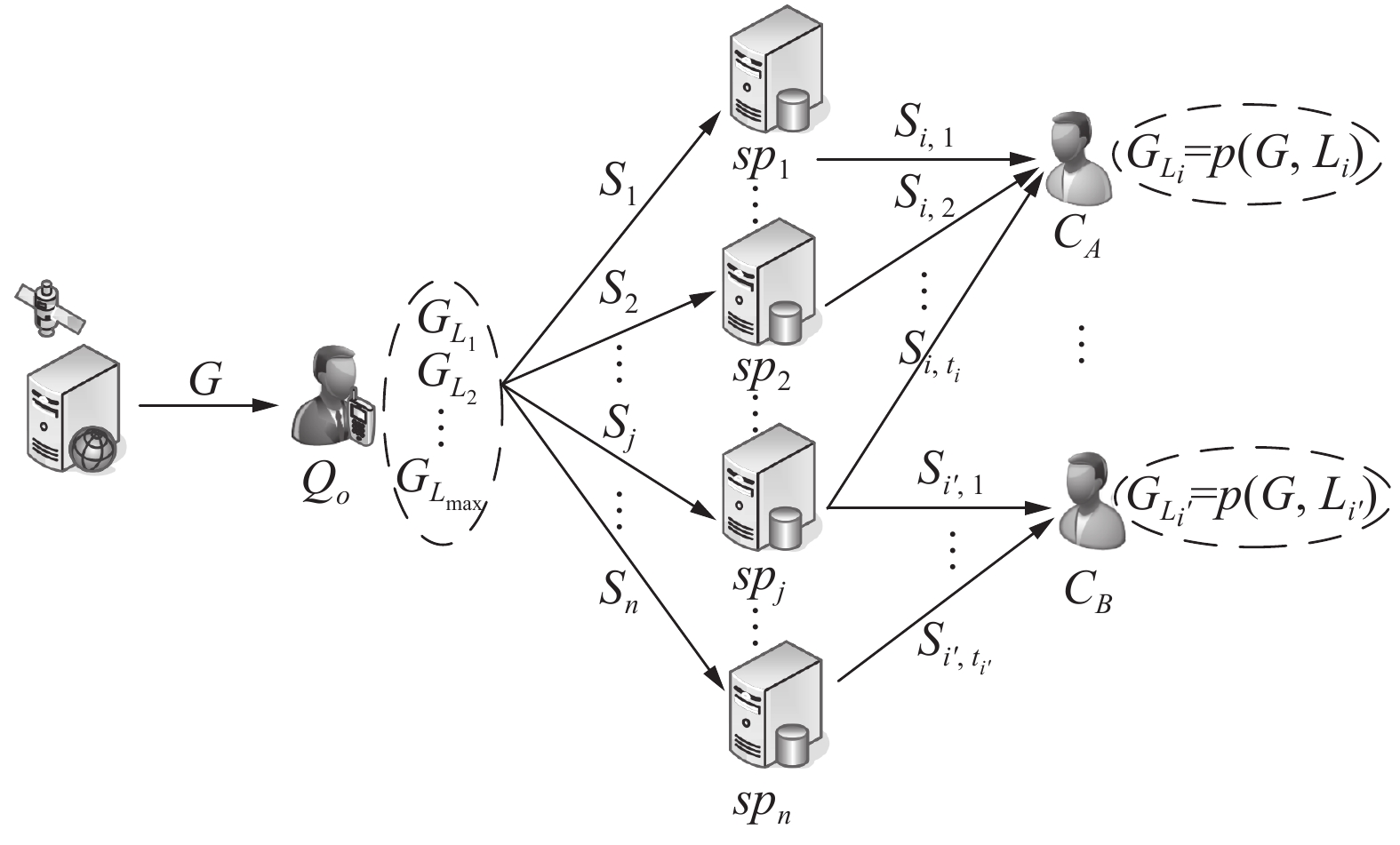 |
| 图2 多用户位置共享隐私保护执行过程示意图 Fig. 2 Implementation of location sharing privacy protection for multi-users |
1)
2)
| $\left\{ \begin{array}{l} {G_{{L_1}}} = p\left( {G,{L_1}} \right), \\ {G_{{L_2}}} = p\left( {G,{L_2}} \right), \\ \quad\quad\quad\vdots \\ {G_{L\max }} = p\left( {G,{L_{\max }}} \right) \\ \end{array} \right.$ | (14) |
3)
4)
5)当
6)被授权访问的
7)
在复杂的移动社交网络中,LBS应用中的隐私威胁主要在于不可信的
引 理 本方案能够实现对
证明:
1)方案的正确性、可行性、有效性在文献[19]中利用多项式形式的中国剩余定理及数论中插值多项式唯一性定理已被详细证明,在此不再赘述。
2)对于任何访问结构,都存在实现该访问结构上完备的秘密共享方案[20],即满足任意授权子集都可以很容易地恢复出秘密,但任意的非授权子集都得不到关于秘密的任何信息。当
3)用户与多个位置服务器的合谋攻击实质上是多个位置服务器合谋攻击的特殊情况[12]。本方案中,即使对应位置精度级
4)假设用户
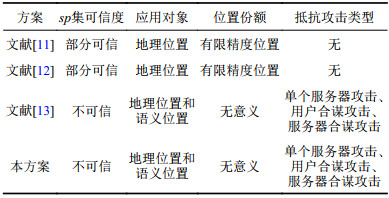
本方案与文献[11-13]方案在是否需要可信sp集、应用对象范围、位置份额、抵抗攻击类型等方面的对比见表1。如表1所示,与同类方案相比,本方案可同时实现地理和语义位置共享的分级隐私保护、抵抗多种常见攻击,安全性高且不依赖于
| 表1 同类方案对比 Tab. 1 Comparison of similar schemes |
 |
2.2 性能分析
本方案的运算主要分为3部分:
实验仿真结果中,
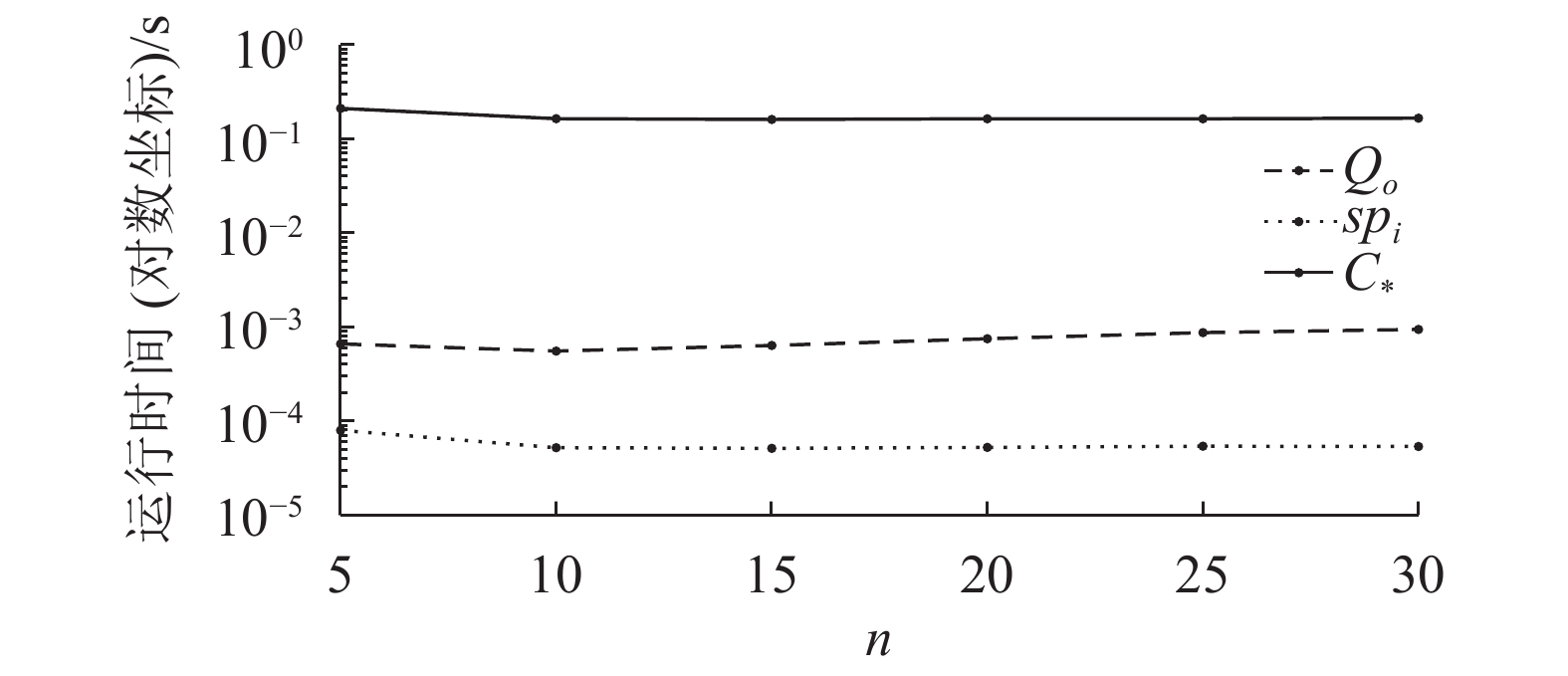 |
| 图3 n变化时的计算时间 Fig. 3 Computation time of changing n |
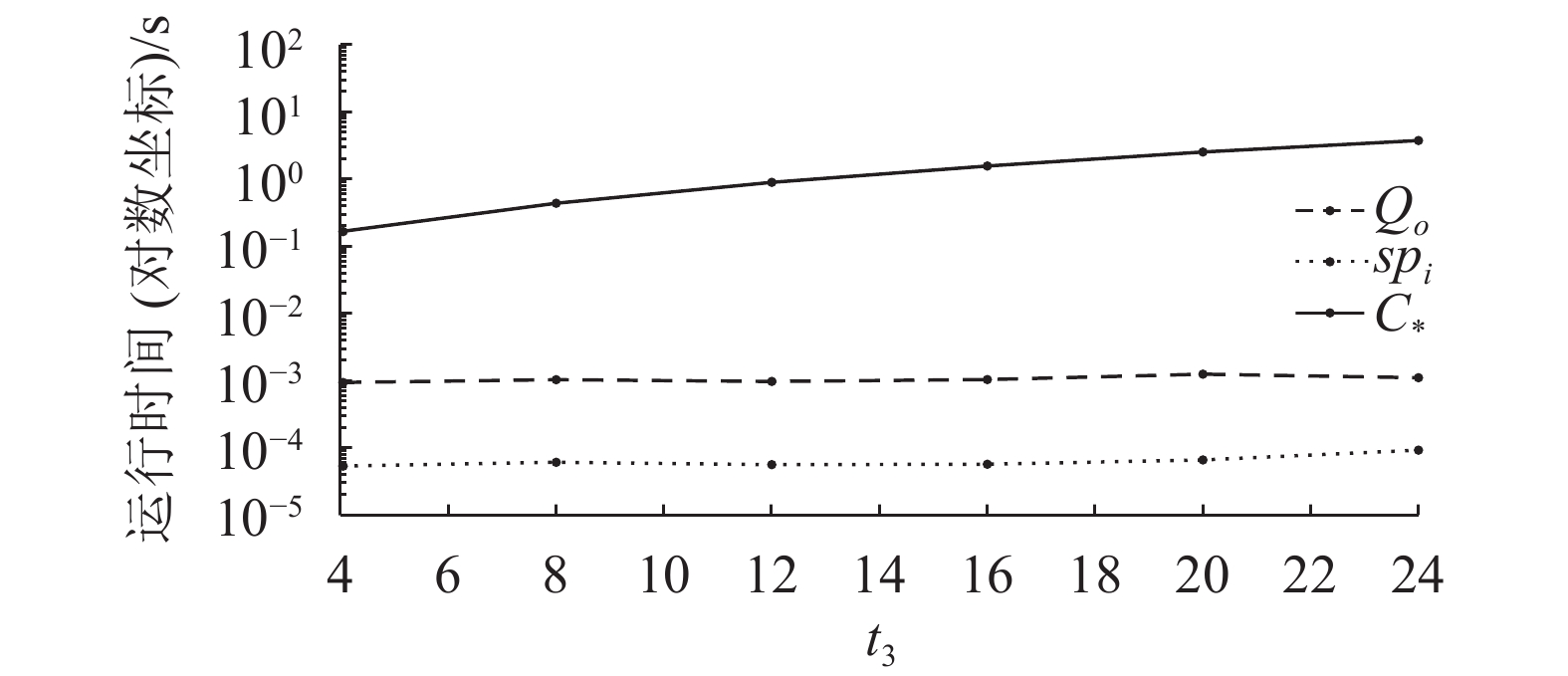 |
| 图4 t3变化时的计算时间 Fig. 4 Computation time of changing t3 |
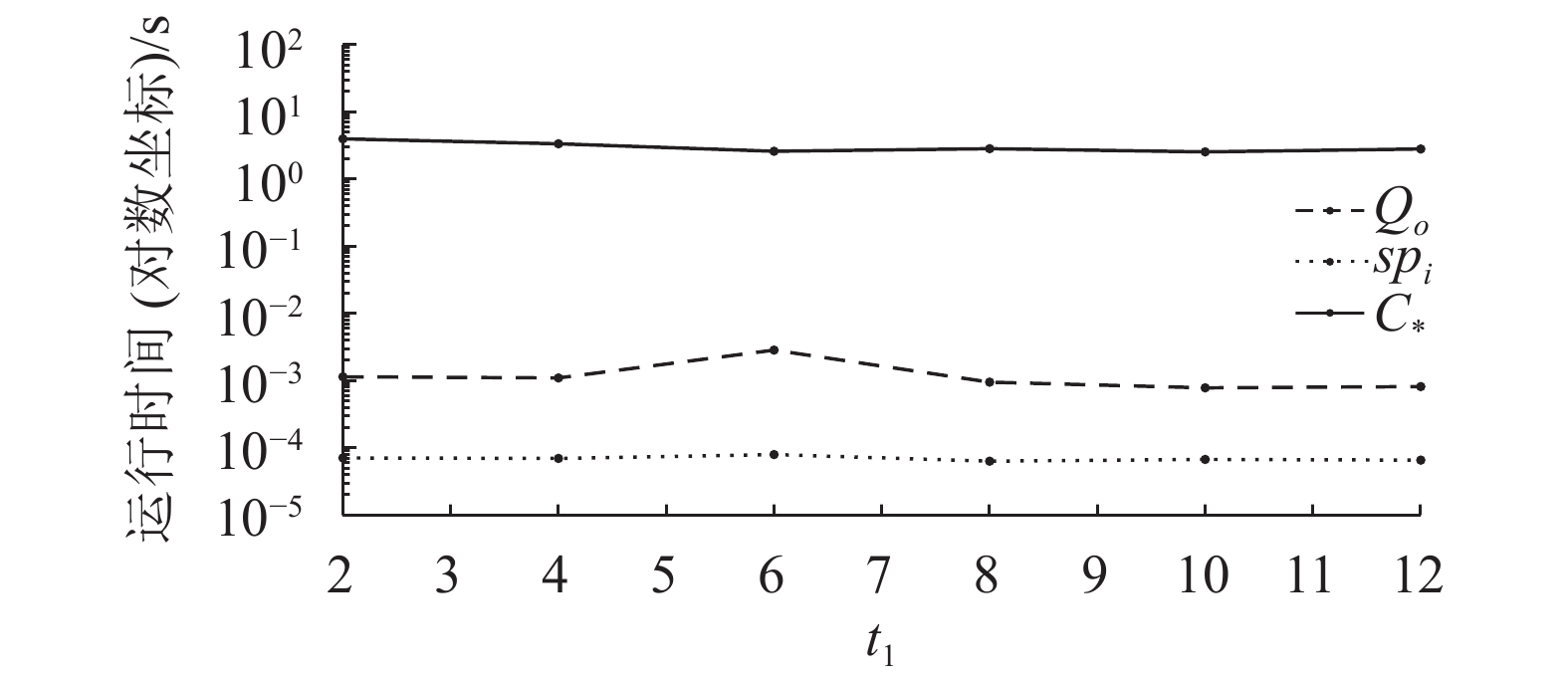 |
| 图5 t1变化时计算时间 Fig. 5 Computation time of changing t1 |
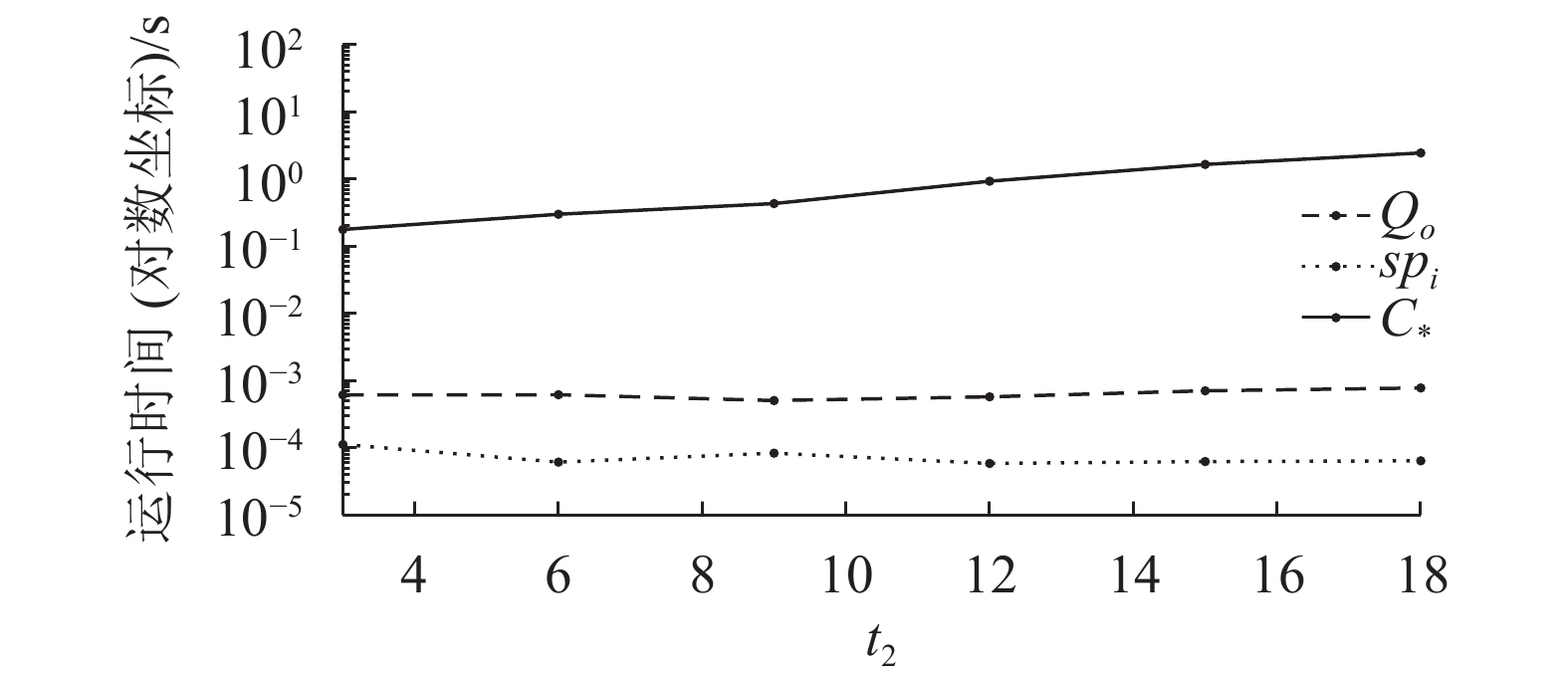 |
| 图6 t2变化时计算时间 Fig. 6 Computation time of changing t2 |
本方案与文献[11-13]方案在运行时间上的对比见表2。如表2所示,即使在加入对大素数的素性判定与选取运算、未采用中国剩余定理快速算法的最坏情况下,本方案的效率相对于同类方案的效率仍然更高,实现简单,计算量小,性能更加稳定。
| 表2 运行时间对比 Tab. 2 Comparison of running time |
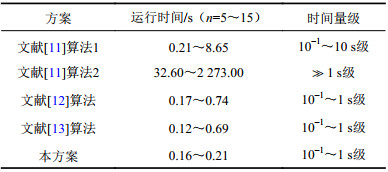 |
这主要是由于本方案将多个不同精度级别的位置信息打包成一个整体,在
若一定时间内
相对于传统“全部或全不”的刚性位置隐私保护策略,弹性的分级隐私保护策略更加符合移动互联网中用户的个性化需求。本方案通过地理和语义位置转换模型保证用户能够灵活地自定义其共享位置的精度级别及可访问对象,并利用基于中国剩余定理的门限可变多秘密共享方法,将定义的多精度级的位置信息作为整体打包转换分割,实现了一次份额分发就能使不同共享对象重构出不同精度的位置信息,在不可信环境下完成了多用户位置共享的弹性隐私保护。仿真实验分析进一步表明,本方案计算复杂度低,通信开销小,鲁棒性好,与同类方案相比更为高效,即使在网络资源受限的环境中和计算能力受限的用户终端上也同样适用。此外,本方案除可应用于好友查找等基于位置共享的社交服务场景外,也可扩展使用至军队信息化层级指挥作战系统,在基于位置共享的群组协同作战领域有着广阔的应用前景。
| [1] |
Wang Yuhang,Zhang Hongli,Yu Xiangzhan. Research on location privacy in mobile Internet[J]. Journal on Communications, 2015, 36(9): 230-243. [王宇航,张宏莉,余翔湛. 移动互联网中的位置隐私保护研究[J]. 通信学报, 2015, 36(9): 230-243. DOI:10.11959/j.issn.1000-436x.2015167] |
| [2] |
Lee B,Oh J,Yu H,et al.Protecting location privacy using location semantics[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’11).New York:ACM,2011:1289–1297.DOI:10.1145/2020408.2020602
|
| [3] |
Kalnis P,Ghinita G,Mouratidis K,et al. Preventing location-based identity inference in anonymous spatial queries[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(12): 1719-1733. DOI:10.1109/TKDE.2007.190662 |
| [4] |
Enserink M,Chin G. The end of privacy[J]. Science, 2015, 347(6221): 490-491. DOI:10.1126/science.347.6221.490 |
| [5] |
Xiong Xingxing,Liu Shubo,Li Dan,et al. Private electric vehicle charging location aggregation based on local differential privacy[J]. Advanced Engineering Sciences, 2019, 51(2): 137-143. [熊星星,刘树波,李丹,等. 基于局部差分隐私的电动汽车充电位置隐私汇聚[J]. 工程科学与技术, 2019, 51(2): 137-143. DOI:10.15961/j.jsuese.201801051] |
| [6] |
Li J,Yan Hongyang,Liu Zheli,et al. Location-sharing systems with enhanced privacy in mobile online social networks[J]. IEEE Systems Journal, 2017, 11(2): 439-448. DOI:10.1109/JSYST.2015.2415835 |
| [7] |
Marias G F,Delakouridis C,Kazatzopoulos L,et al.Location privacy through secret sharing techniques[C]//Proceedings of the Sixth IEEE International Symposium on a World of Wireless Mobile and Multimedia Networks.Taormina-Giardini Naxos:IEEE,2005:614–620.
|
| [8] |
Dürr F,Skvortsov P,Rothermel K.Position sharing for location privacy in non-trusted systems[C]//Proceedings of the 2011 IEEE International Conference on Pervasive Computing and Communications (PerCom).Seattle:IEEE,2011:189–196.
|
| [9] |
Skvortsov P,Dürr F,Rothermel K.Map-aware position sharing for location privacy in non-trusted systems[M]//Pervasive Computing.Berlin:Springer,2012:388–405.
|
| [10] |
Wernke M,Dürr F,Rothermel K.PShare:Position sharing for location privacy based on multi-secret sharing[C]//Proceedings of the 2012 IEEE International Conference on Pervasive Computing and Communications.Lugano:IEEE,2012:153–161.
|
| [11] |
Wernke M,Dürr F,Rothermel K.Efficient position sharing for location privacy using binary space partitioning[M]// Mobile and Ubiquitous Systems:Computing,Networking,and Services.Berlin:Springer,2013:263–275.
|
| [12] |
Wernke M,Dürr F,Rothermel K. PShare:Ensuring location privacy in non-trusted systems through multi-secret sharing[J]. Pervasive and Mobile Computing, 2013, 9(3): 339-352. DOI:10.1016/j.pmcj.2013.01.001 |
| [13] |
Skvortsov P,Schembera B,Dürr F,et al.Optimized secure position sharing with non-trusted servers[EB/OL].(2017–02–27)[2019–09–01].https://arxiv.org/abs/1702.08377.
|
| [14] |
Kinateder M,Baschny E,Rothermel K.Towards a generic trust model—Comparison of various trust update algorithms[M]//Trust Management.Berlin:Springer,2005:177–192.
|
| [15] |
Sadilek A,Kautz H,Bigham J P.Finding your friends and following them to where you are[C]//Proceedings of the Fifth ACM International Conference on Web Search and Data Mining (WSDM’12).New York:ACM,2012:723–732.
|
| [16] |
Strassman M.2-Case study:Development of the find friend application[M]//Location-based Services.Holland:Elsevier,2004:27–39.
|
| [17] |
Li Huixian.Study on theory and application of multi-secret sharing[D].Dalian:Dalian University of Technology,2006:44–50. 李慧贤.多秘密共享理论及其应用研究[D].大连:大连理工大学,2006:44–50. |
| [18] |
Tyagi A,Sreenath N. A comparative study on privacy preserving techniques for location based services[J]. British Journal of Mathematics & Computer Science, 2015, 10(4): 1-25. DOI:10.9734/bjmcs/2015/16995 |
| [19] |
Chan Chaowen,Chang C C. A scheme for threshold multi-secret sharing[J]. Applied Mathematics and Computation, 2005, 166(1): 1-14. DOI:10.1016/j.amc.2004.04.081 |
| [20] |
Benaloh J,Leichter J.Generalized secret sharing and monotone functions[M]//Advances in Cryptology — CRYPTO’88.New York:Springer,1990:27–35.
|
| [21] |
Asmuth C,Bloom J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, 29(2): 208-210. DOI:10.1109/TIT.1983.1056651 |
 2020, Vol. 52
2020, Vol. 52


