2. 四川大学 水力学与山区河流开发保护国家重点实验室,四川 成都 610065
2. State Key Lab. of Hydraulics and Mountain River Eng., Sichuan Univ., Chengdu 610065, China
目前,滑坡稳定性的定量计算方法可分为确定性计算方法和可靠度计算方法。传统的确定性分析方法主要采用极限平衡分析方法、强度折减法等计算坡体的安全系数,在实际工程中得到了广泛的应用。但由于坡体存在荷载环境、结构特征、岩土体特性参数等诸多不确定性因素,采用以概率统计为基础的可靠度分析方法计算滑坡的破坏概率和可靠度,比用安全系数在一定程度上能更客观、定量地反映滑坡的安全性[1],并可以为滑坡灾害的定量风险评价提供依据[2],近年来在滑坡工程中日益得到重视。
2018年10月10日和11月3日,西藏自治区江达县波罗乡白格村金沙江右岸先后两次发生大规模高位滑坡,堵塞金沙江,堰塞湖与溃坝洪水给金沙江上游沿岸居民及其生产和生活设施带来巨大灾害。白格滑坡及其导致的滑坡堵江–溃坝洪水灾害链受到了国内外的广泛关注,诸多学者对滑坡的地质环境条件、变形破坏机制及发展趋势进行了研究。许强等[3]结合现场调查和历史遥感影像解译等手段,分析了滑坡区斜坡的变形历史和动态演化过程,以及两次滑坡–堰塞堵江的基本特征。邓建辉等[4]基于现场调查对滑坡的形成机制与过程进行了系统分析。张永双等[5]从地质角度剖析了白格滑坡的地质成因,提出了金沙江构造缝合带混杂岩体岸坡在持续重力作用下的失稳机理。自2018年连续两次滑坡发生之后,白格滑坡后缘出现3个裂缝区(图1),一旦失稳,再次堵江的危险性较大[4]。因此,裂缝区的发展趋势和稳定性成为目前面临的关键难题。冯文凯等[6]基于裂缝区形貌特征和变形迹象对其变形破坏特征和发展趋势进行了分析。陈菲等[7]结合地质和监测资料对裂缝区的发展趋势进行了分析和预测。王立朝[8]和Fan[9]等分别采用2维离散元模拟软件UDEC和3维有限差分软件FLAC3D对裂缝区稳定性进行了定量数值模拟,由于缺乏现场试验参数,定量分析采用的均为经验参数,难以反映滑坡岩土体的真实性状。
 |
| 图1 白格滑坡平面图 Fig. 1 Overview of Baige landslide |
鉴于白格滑坡地质结构的复杂性和岩土体物理力学参数的不确定性,采用可靠度方法对白格滑坡进行参数反演和裂缝区失稳概率分析,对于滑坡灾害的风险评价及处置具有重要意义。
1 白格滑坡地质环境条件白格滑坡地处青藏高原东部,属横断山区北部,芒康山与沙鲁里山间的金沙江河谷地带,为典型的构造高山峡谷侵蚀地貌。滑坡位于金沙江右岸,前缘为金沙江凹岸,平水位高程2 880 m;后缘为一走向N19°E的条形山脊,高程约3 730 m。滑坡坡向80°~100°,坡度上下陡、中间缓,相对高差达850 m,平均坡度约33°。
滑坡区位于金沙江缝合带上,由于受多期构造运动的影响,区域构造形迹较为复杂。主要断裂构造形迹为近北南向的江达—波罗金沙江断裂带及NW向断裂。根据现场调查及勘查报告[10],滑坡区出露岩性以片麻岩为主,中前部为片麻岩夹碳质板岩,岩层产状倾向(180°~220°)、倾角(∠36°~∠42°);中部到后缘范围为蛇纹石化片麻岩,在斜坡顶部结晶良好,墨绿色;中下部呈碎粉岩状,灰绿色,绿泥石化,具有多期、多次变形与变质特点。滑坡体典型剖面如图2所示。
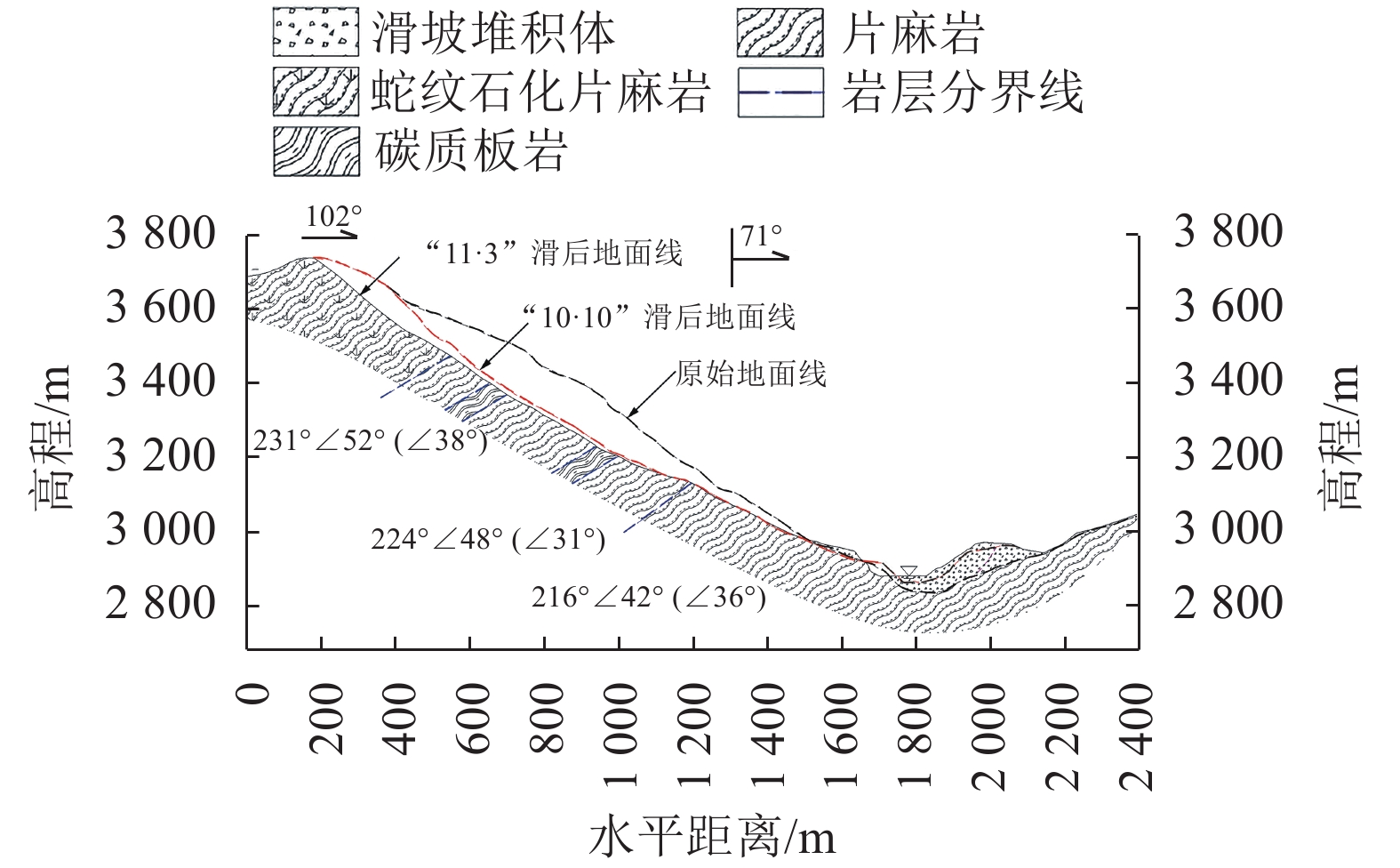 |
| 图2 白格滑坡剖面图(1–1′剖面) Fig. 2 Cross section of Baige landslide (1–1′ section) |
滑坡按高程划分为3区,即前缘的阻滑区、中部的主滑区和后缘的牵引区,分割高程大致为3 500 m和3 000 m。主滑区为楔形体,系两组发育良好的结构面切割形成;阻滑区为四面体,由两组发育较差的结构面切割形成;牵引区为完全风化的岩土体夹团块状碎裂岩体。白格“10·10”滑坡是相对完整的阻滑区岩体在主滑区重力驱动下的渐进破坏过程,方量约107 m3。主滑区楔形体重力是滑坡的主要动力来源,滑坡的孕育过程中,白格“11·3”滑坡是牵引区的部分岩土体在起阻滑作用的碎裂岩体渐进解体后下滑的结果,方量约3×106 m3[2]。
在连续两次滑坡事件发生之后,受失稳滑体牵引拖拽作用以及临空卸荷作用的影响,在滑坡体后缘及两侧出现多条深大裂缝,形成3个裂缝区(图1)。综合现场调查、监测及地质分析[5],各区域的范围及发展趋势为:C1区位于滑坡体下游侧边界,面积约2.3×105 m2,厚度15~95 m,可分为3个亚区,变形速率最快的为C1–1区,体积约7×105 m3;C2区位于滑坡体后缘,面积约7.3×104 m2,厚度45~70 m,可分为2个亚区,潜在失稳范围为C2–1区,体积约3.2×106 m3;C3区位于滑坡体上游侧边界,面积约1.2×105 m2,厚度20~30 m,体积约1.9×106 m3,可分为2个亚区,其中C3–1区体积约1.3×106 m3。各裂缝区典型地质剖面如图3所示,ZK表示钻孔位置和编号。
 |
| 图3 裂缝区剖面图 Fig. 3 Cross section of crack zones |
2 白格“11·3”滑坡参数反演 2.1 基于极大似然的优化算法
在滑坡可靠度分析中,滑坡的破坏概率与坡体抗剪强度参数的统计特征密切相关。受现场条件及试验方法限制,试验数量有限,试验成果往往难以准确地反映坡体抗剪强度参数的统计特征。贝叶斯分析方法能够将岩土体参数先验信息和有限的场地信息有机结合,在概率反演边坡抗剪强度参数和渗透系数等方面逐渐得到应用[11]。Zhang等[12]提出了基于极大似然估计的优化算法,优化过程可以在电子表格实现。Zhang等[13]采用马尔可夫链蒙特卡洛(MCMC)方法对多层土体抗剪强度参数同时进行反分析,有效地解决了边坡反分析中多参数反演问题。Wang等[14]分别采用MCMC方法和极大似然估计对台湾3号高速公路滑坡抗剪强度参数和锚固力参数进行了非确定性反演,表明上述两种方法的计算结果均与现场调查和勘测结果一致,基于极大似然估计的优化算法计算工作量小,更适用于滑坡事后调查和评估。基于极大似然估计的优化算法基本原理如下:
设
| $\varepsilon = y - g({{\theta}} )$ | (1) |
式中:
基于以上假设,
对于出现失稳的滑坡,
| $\begin{aligned}[b] S({{\theta}} ) =& \dfrac{{{{\left[ {g({{\theta}} ) + {{{\mu}} _\varepsilon } - 1} \right]}^{\rm T}}\left[ {g({{\theta}} ) + {{{\mu}} _\varepsilon } - 1} \right]}}{{\partial {{\theta}} }} + \\ &{\left[ {{{\theta}} - {{{\mu}} _{ \theta }}} \right]^{\rm T}}{{C}}_{{\theta}} ^{ - 1}\left[ {{{\theta}} - {{{\mu}} _{ \theta }}} \right] \\ \end{aligned} $ | (2) |
随机参数向量
| ${{{C}}_{{ \theta }\left| d \right.}} = {\left( {\frac{{{{{G}}^{\rm{T}}}{{G}}}}{{{{\sigma }}_\varepsilon ^{\rm{2}}}} + {{C}}_{{\theta}} ^{ - 1}} \right)^{ - 1}}$ | (3) |
| ${{G}} = \frac{{\partial g({{\theta}} )}}{{\partial {{\theta}} }}\left| {_{{{\theta}} = {{\mu}} _{{{\theta}} \left| d \right.}}} \right.$ | (4) |
Zhang等[12]将上述方法称为基于优化的反分析方法,其优化过程可以在Excel中实现,计算简便。
2.2 参数反演分析 2.2.1 安全系数计算模型边坡稳定性反分析一般是极限平衡分析方法。在极限平衡分析方法中,Morgenstern–Price法满足严格平衡条件,收敛性良好,并能对任意形状的滑动面进行分析,因此得到了广泛应用。在概率反分析优化过程中,需要重复调用安全系数的计算模型并对其进行求导,而Morgenstern–Price法的安全系数计算公式为隐函数,无法写出显式状态方程[15],其使用具有一定局限。为克服这一问题,采用响应面法(response surface method, RSM)对安全系数计算模型进行拟合。
现场调查及监测表明,白格“11·3”滑坡坡体内无明显地下水,影响滑坡稳定性最主要的参数是滑坡岩土体的抗剪强度指标黏聚力
| $ g({{\theta}} ) = {a_0} + \sum\limits_{i = 1}^n {{b_i}{{{\theta}} _i}} + \sum\limits_{i = 1}^n {{c_i}} {{\theta }}_i^2 $ | (5) |
式中:
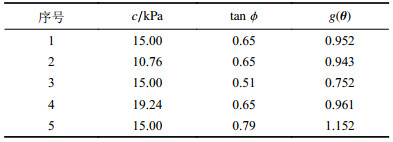
| 表1 中心复合设计取样点及安全系数 Tab. 1 Sampling points by central composite design and corresponding safety factor |
 |
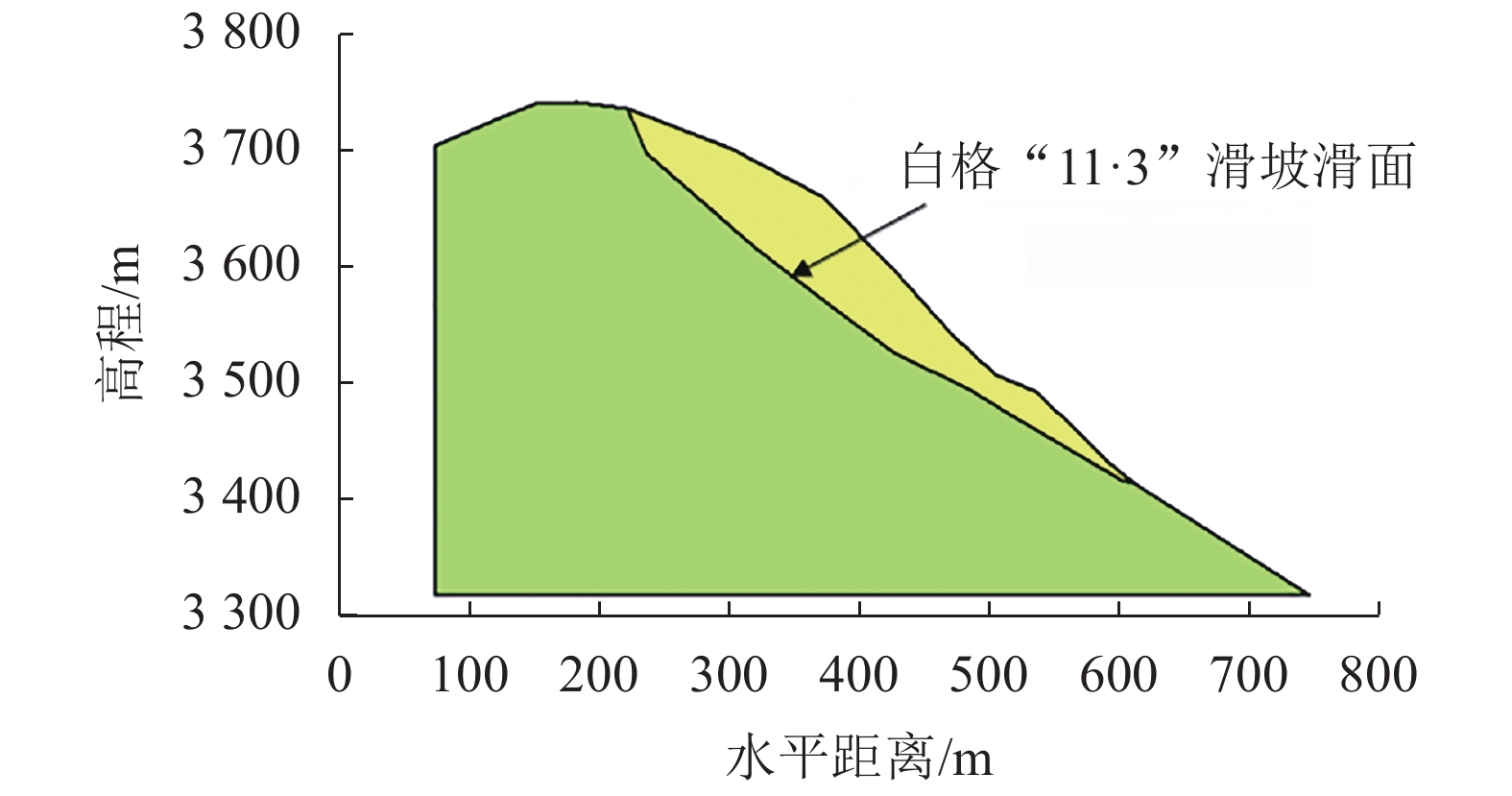 |
| 图4 白格 “11·3”滑坡安全系数计算模型 Fig. 4 LEM model of Baige “11·3” landslide |
将表1中的数据代入式(5),进行响应面求解,得到滑坡安全系数计算模型的响应面近似方程为:
| $g\left( {{\theta}} \right) = 0.000\;{\rm{ }}8 + 0.002\;{\rm{ }}1c + 1.414\;{\rm{ }}4\tan \; \phi $ | (6) |
式中,
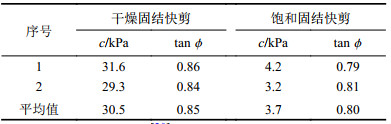
根据坡体强风化蛇纹岩的室内直剪试验结果(表2)及相关文献[19],随机参数向量的先验分布的黏聚力和内摩擦角分别可以取为
| 表2 直剪试验结果 Tab. 2 Results of direct shear test |
 |
| ${{C}}{\rm{(}}{{\theta}} {\rm{)}} = \left[\! {\begin{array}{*{20}{c}} {{3^2}}&0 \\ 0&{0.{1^2}} \end{array}}\! \right]$ | (7) |
根据Christian等[20]的研究,简化Bishop法的模型误差服从均值0.05、标准差0.07的正态分布。考虑到Morgenstern–Price法与简化Bishop法的计算结果一般比较接近,且Morgenstern–Price法满足力的严格平衡条件,因此假设安全系数计算模型
根据第2.2.1和2.2.2节计算模型和参数,采用Excel建立式(2)~(4)的电子计算表格;并采用Excel的规划求解功能,通过使式(2)的
经过优化求解,求得随机参数向量的后验分布黏聚力和内摩擦角可分别取为
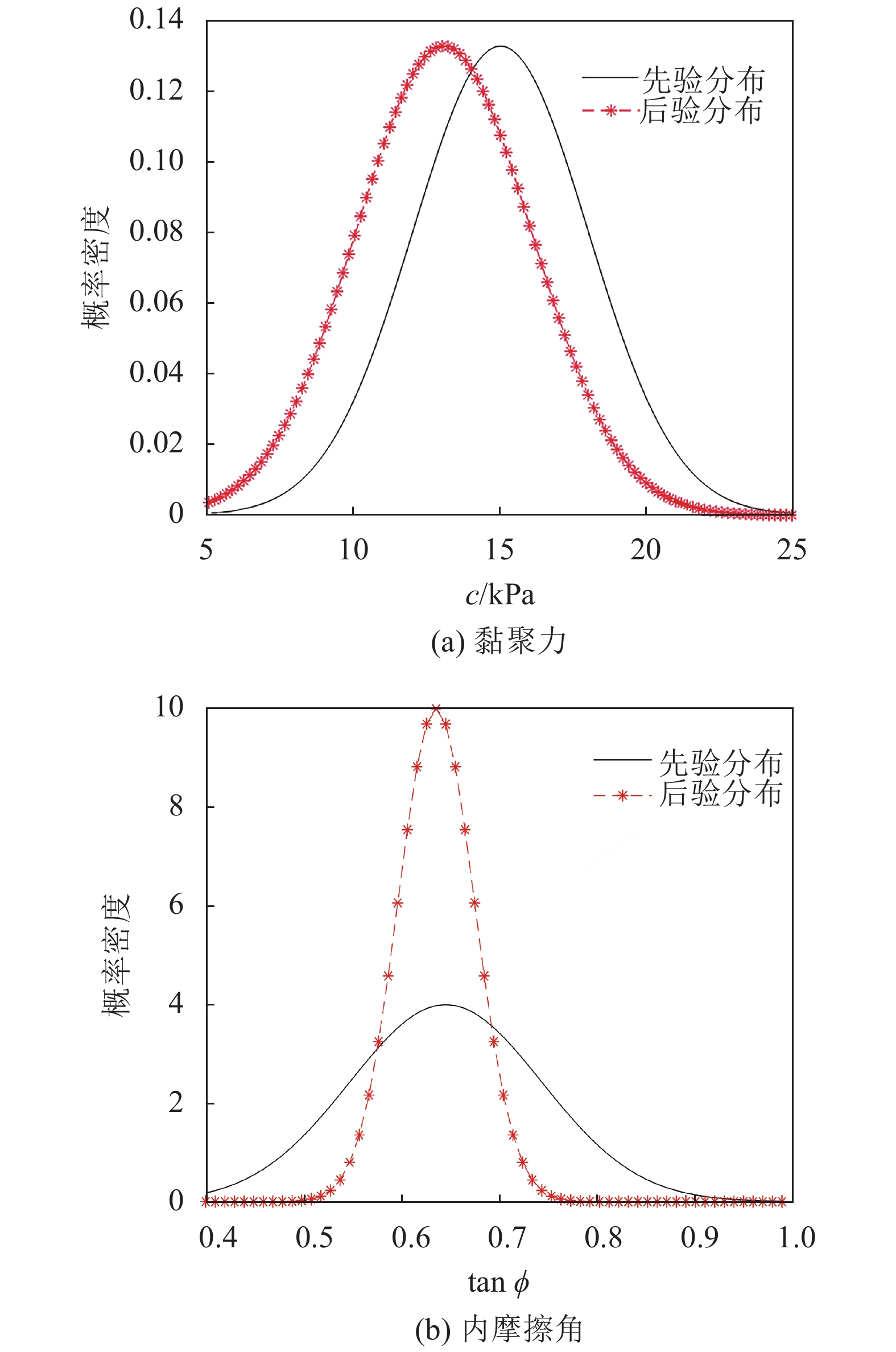 |
| 图5 随机参数向量先验分布与后验分布对比 Fig. 5 Comparison of prior and posterior distribution |
3 后缘裂缝区可靠度分析
由于白格“11·3”滑坡滑源区与后缘裂缝区位于同一高程,岩性基本一致。因此,采用第2.2.3节白格“11·3”滑坡的参数反演分析结果,对后缘各裂缝区的失稳概率进行可靠度分析。计算方法为蒙特卡洛法,采用GeoStudio软件进行计算。计算时,针对每个典型剖面(图3)均考虑两种破坏模式:一是,整体破坏模式,以勘探及监测确定的潜在滑动面作为确定性滑面进行计算;二是,局部破坏模式,由软件自动搜索最危险滑动面,如图6所示。
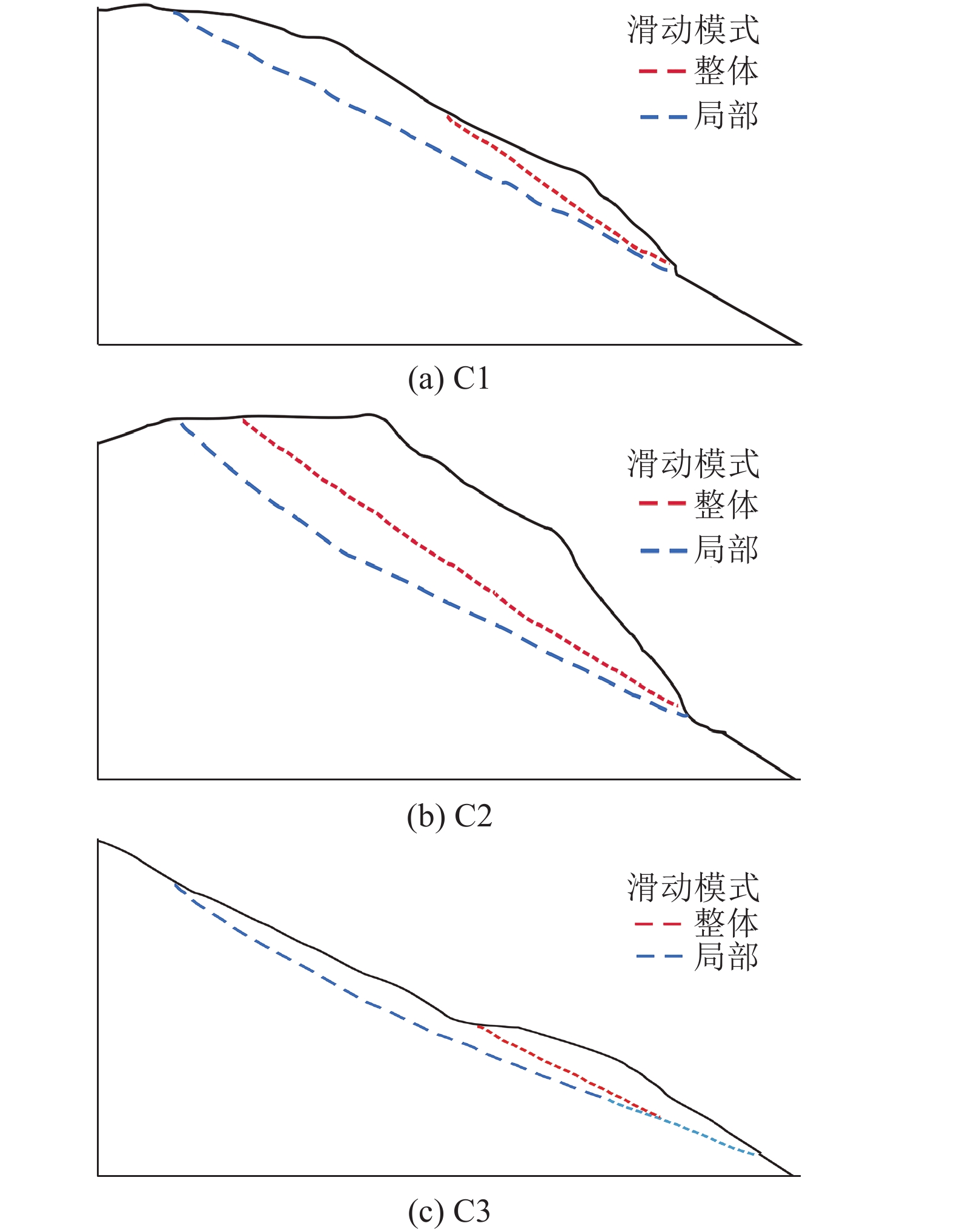 |
| 图6 白格滑坡后缘裂缝区潜在破坏模式 Fig. 6 Failure mode of potential failure mode in the rear fracture zones of Baige landslide |
由图6可知:裂缝区C1自动搜索的最危险滑动区范围与监测得到的变形速率最大的C1–1区范围基本一致。同样,裂缝区C2、C3自动搜索的最危险滑动区范围也分别对应裂缝区前部的潜在失稳区C2–1和C3–1。
表3为各裂缝区的破坏模式及相应的失稳概率计算结果。
| 表3 白格“11·3”滑坡后缘裂缝区可靠度计算结果 Tab. 3 Reliability calculation results of the fracture zone at the rear edge of Baige “11·3” landslide |
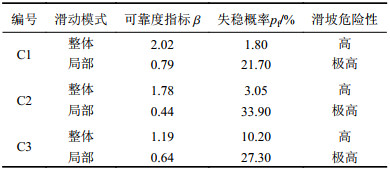 |
由表3可知:各裂缝区在局部破坏模式下,其破坏概率均明显大于整体破坏模式,表明裂缝区破坏以渐进牵引破坏为主,与实际的裂缝发展规律及破坏模式一致。根据文献[9]的滑坡半定量标准,可通过失稳概率判断滑坡的危险性:
针对白格“11·3”滑坡,采用基于极大似然估计的优化算法对滑坡岩土体的抗剪强度参数进行了反演,并利用反演参数,对滑坡后缘裂缝区进行了可靠度分析,主要结果如下:
1)本文将响应面法与基于极大似然的概率反分析方法结合起来,对白格“11·3”滑坡滑坡体不确定参数进行反演,计算过程简便,计算方法适应性强。
2)通过对白格“11·3”滑坡抗剪强度参数进行反演,得到滑坡岩土体抗剪强度后验分布的黏聚力和内摩擦角分别为
3)采用反演参数对白格“11·3”滑坡后缘3个裂缝区的整体和局部稳定性进行了可靠度分析。各裂缝区在局部破坏模式下的最危险滑动区范围与现场调查及监测得到的失稳区范围基本一致,且局部破坏模式下的破坏概率均明显大于整体破坏模式,表明裂缝区破坏以渐进牵引破坏为主,与实际的裂缝发展规律及破坏模式一致。
4)白格“11·3”滑坡后缘3个裂缝区的潜在失稳区域C1–1、C2–1和C3–1的体积分别为7×105 m3、3.2×106 m3和1.3×106 m3,对应的失稳概率分别为21.70%、33.90%和27.30%,均为极高危险性。类比白格“11·3” 滑坡堵江事件,裂缝区如再次启动,特别是方量较大、失稳概率最高的C2–1区如再次启动,堵江的危险性较大。有必要根据可靠度计算结果,对滑坡堵江–溃坝灾害链进行风险评价,并提出合理的处置措施和应急预案。
5)鉴于白格“11·3”滑坡后缘3个裂缝区已逐步连通,裂缝区之间的变形和稳定性存在相互影响。如何考虑裂缝区之间的相互作用机制,从系统可靠度的角度对其总体稳定性进行评价,有待进一步进行研究。
| [1] |
吴树仁,石菊松,王涛.滑坡风险评估理论与技术[M].北京:科学出版社,2012.
|
| [2] |
殷坤龙,张桂荣,陈丽霞,等.滑坡灾害风险分析[M].北京:科学出版社,2010.
|
| [3] |
Xu Qiang,Zheng Guang,Li Weile,et al. Study on successive landslide damming events of Jinsha River in Baige village on Octorber 11 and November 3,2018[J]. Journal of Engineering Geology, 2018, 26(6): 1534-1551. [许强,郑光,李为乐,等. 2018年10月和11月金沙江白格两次滑坡–堰塞堵江事件分析研究[J]. 工程地质学报, 2018, 26(6): 1534-1551. DOI:10.13544/j.cnki.jeg.2018-406] |
| [4] |
Deng Jianhui,Gao Yunjian,Yu Zhiqiu,et al. Analysis on the formation mechanism and process of Baige landslides damming the upper reach of Jinsha River,China[J]. Advanced Engineering Sciences, 2019, 51(1): 9-16. [邓建辉,高云建,余志球,等. 堰塞金沙江上游的白格滑坡形成机制与过程分析[J]. 工程科学与技术, 2019, 51(1): 9-16. DOI:10.15961/j.jsuese.201801438] |
| [5] |
Zhang Yongshuang,Ba Renji,Ren Sanshao,et al.Analysis on geo-mechanism of the Baige landslide in Jinsha River,Tibet,China[J/OL].Geology in China[2020–03–10].http://kns.cnki.net/kcms/detail/11.1167.p.20191228.1302.004.html. 张永双,巴仁基,任三绍,等.中国西藏金沙江白格滑坡的地质成因分析[J/OL].中国地质[2020–03–10].http://kns.cnki.net/kcms/detail/11.1167.p.20191228.1302.004.html. |
| [6] |
Feng Wenkai,Zhang Guoqiang,Bai Huilin,et al. A preliminary analysis of the formation mechanism and development tendency of the huge Baige landslide in Jinsha River on October 11,2018[J]. Journal of Engineering Geology, 2019, 27(2): 415-425. [冯文凯,张国强,白慧林,等. 金沙江“10·11”白格特大型滑坡形成机制及发展趋势初步分析[J]. 工程地质学报, 2019, 27(2): 415-425. DOI:10.13544/j.cnki.jeg.2018-392] |
| [7] |
Chen Fei,Wang Sai,Gao Yunjian,et al. Evolution of the cracking zones at the site of the Baige landslides and their future development[J]. Advanced Engineering Sciences, 2020, 52(5): 71-78. [陈菲,王塞,高云建,等. 白格滑坡裂缝区演变过程及其发展趋势分析[J]. 工程科学与技术, 2020, 52(5): 71-78. DOI:10.15961/j.jsuese.202000246] |
| [8] |
Wang Lichao,Wen Mingsheng,Feng Zhen,et al. Researches on the Baige landslide at Jinshajiang River,Tibet,China[J]. The Chinese Journal of Geological Hazard and Control, 2019, 30(1): 1-9. [王立朝,温铭生,冯振,等. 中国西藏金沙江白格滑坡灾害研究[J]. 中国地质灾害与防治学报, 2019, 30(1): 1-9. DOI:10.16031/j.cnki.issn.1003-8035.2019.01.01] |
| [9] |
Fan Xuanmei,Yang Fan,Siva Subramanian S,et al. Prediction of a multi-hazard chain by an integrated numerical simulation approach:The Baige landslide,Jinsha River,China[J]. Landslides, 2020, 17: 147-164. DOI:10.1007/s10346-019-01313-5 |
| [10] |
吴新明,曹水合,吴典坤,等.西藏自治区昌都市江达县波罗乡金沙江白格滑坡勘查报告[R].眉山:地矿眉山工程勘察院,2019.
|
| [11] |
Jiang Shuihua,Wei Bowen,Zhang Wenju,et al. Probabilistic back analysis of spatially varying soil properties and reliability updating of slopes with multiple sources of test data[J]. Rock and Soil Mechanics, 2018, 39(4): 1491-1499. [蒋水华,魏博文,张文举,等. 基于多源试验数据空间变异土体参数概率反演及边坡可靠度更新[J]. 岩土力学, 2018, 39(4): 1491-1499. DOI:10.16285/j.rsm.2016.2257] |
| [12] |
Zhang J,Tang W H,Zhang L M. Efficient probabilistic back-analysis of slope stability model parameters[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1): 99-109. DOI:10.1061/(asce)gt.1943-5606.0000205 |
| [13] |
Zhang L L,Zhang J,Zhang L M,et al. Back analysis of slope failure with Markov chain Monte Carlo simulation[J]. Computers and Geotechnics, 2010, 37(7/8): 905-912. DOI:10.1016/j.compgeo.2010.07.009 |
| [14] |
Wang Lei,Hwang J H,Luo Zhe,et al. Probabilistic back analysis of slope failure—A case study in Taiwan[J]. Computers and Geotechnics, 2013, 51: 12-23. DOI:10.1016/j.compgeo.2013.01.008 |
| [15] |
Chen Changfu,Zhu Jianfeng,Gong Xiaonan. Calculation method of earth slope reliability based on response surface method and Morgenstern–Price procedure[J]. Engineering Mechanics, 2008, 25(10): 166-172. [陈昌富,朱剑锋,龚晓南. 基于响应面法和Morgenstern–Price法土坡可靠度计算方法[J]. 工程力学, 2008, 25(10): 166-172.] |
| [16] |
张璐璐,张洁,徐耀.岩土工程可靠度理论[M].上海:同济大学出版社,2011.
|
| [17] |
Li Dianqing,Zheng Dong,Cao Zijun,et al. Comparison among response surface methods for slope reliability analysis[J]. Engineering Journal of Wuhan University, 2017, 50(1): 1-17. [李典庆,郑栋,曹子君,等. 边坡可靠度分析的响应面方法比较研究[J]. 武汉大学学报(工学版), 2017, 50(1): 1-17. DOI:10.14188/j.1671-8844.2017-01-001] |
| [18] |
GEO-SLOPE International Ltd.边坡稳定性分析软件SLOPE/W用户指南[M].中仿科技(CnTech)公司,译.北京:冶金工业出版社,2011.
|
| [19] |
Phoon K K,Kulhawy F H. Evaluation of geotechnical property variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 625-639. DOI:10.1139/t99-039 |
| [20] |
Christian J T,Ladd C C,Baecher G B. Reliability applied to slope stability analysis[J]. Journal of Geotechnical Engineering, 1994, 120(12): 2180-2207. DOI:10.1061/(asce)0733-9410(1994)120:12(2180) |
 2020, Vol. 52
2020, Vol. 52


