2. 桂林理工大学 土木与建筑工程学院,广西 桂林 541004;
3. 广西岩土力学与工程重点实验室,广西 桂林 541004
2. School of Civil and Architectural Eng., Guilin Univ. of Technol., Guilin 541004, China;
3. Guangxi Key Lab. of Geomechanics and Geotechnical Eng., Guilin 541004, China
岩石在外荷载作用下发生的蠕变变形破坏对深部隧道、巷道和高应力边坡的岩体支护有很大影响。当岩体处于高温、高地应力、强扰动和高地压等复杂地质环境时所呈现的力学性质与常规应力状态下存在明显差异。岩体的变形不仅与外荷载有关,也与时间密切相关,呈现出明显的流变特征,且随着围压逐渐增大,围岩由脆性破坏转化为延性破坏,围岩强度(黏聚力)会随着应力和时间变化产生一定程度的劣化,进而使围岩承载力快速下降,最终导致围岩整体失稳破坏。因此,揭示围岩的蠕变失稳破坏机理尤为重要。例如:Zhou等[1]根据临界裂纹扩展理论,结合PFC2D软件,提出一种可以描述堆石体蠕变行为的随机虚拟裂纹DEM模型;Chen等[2]基于不同温度下花岗岩蠕变行为的试验研究,结合损伤演化过程构建了基于热损伤机理的蠕变模型,描述花岗岩在不同温度和不同时间作用下的蠕变变形;Shi[3]对组合应力场中裂纹扩展问题进行探讨,结合以往试验研究结果提出一种确定结构在组合应力条件下临界裂缝尺寸的方法;张玉等[4]对含膏质泥岩进行高温高围压蠕变系列试验,提出指数损伤演化模型和多元函数型加速蠕变模型,揭示了高温高围压软岩蠕变变形机理;Liu[5]采用分数阶黏壶替代传统西原模型中的黏性元件,且假设岩石蠕变参数是与时间相关的变量参数,从而得到岩石的非线性变化参数蠕变模型;Fahimifar等[6]通过构建描述岩石黏塑性蠕变变形的黏塑料缓冲元件,建立可描述岩石蠕变变形全过程的蠕变模型,并采用数值有限差分法及其内置的FISH语言对本构模型进行二次开发,然后对隧道围岩在荷载作用下时效性变形进行模拟。
上述研究对不同条件下岩体进行蠕变试验,通过不同方法建立可描述蠕变全过程的蠕变模型,可知,由于岩体本身和工程地质环境的差异,还难以建立统一的蠕变模型研究和预测不同情况下的岩石蠕变规律。因此,对岩石蠕变变形破坏机理的研究还有待深入[7-8]。
不仅深部岩体具有明显的流变特性,浅部岩体在强扰动作用下的强度和变形也会呈现时效性。岩石在外荷载及外界强扰动作用下,长期蠕变变形将伴随新生裂隙产生,岩体强度也呈现出下降趋势,且蠕变特性参数也会随着时间出现损伤劣化,最终导致各种宏观与局部破坏现象发生。为进一步揭示蠕变变形破坏的内在机理,预测随时间推移岩体的蠕变变形规律,丁志坤等[9]提出一种改进的非定常广义开尔文蠕变模型;蔡煜等[10]结合Lemaitre应变等效原理建立非定常Burgers模型。这些研究验证了非定常模型可更好地描述岩石的蠕变特性。Zhang[11]、何志磊[12]等基于分数阶理论建立可以克服传统西原体难以描述加速蠕变问题的非线性模型,很好地解决了岩石蠕变的非线性特性;韩阳[13]、刘开云[14]等考虑弹性模量随时间的弱化规律,采用非线性黏壶元件改进Burgers模型,并基于非定常Burgers模型的蠕变方程,建立非定常非线性模型。上述研究中,对于模型参数的确定都是基于试验数据进行反演,但在确定蠕变参数时,参数没有一个明确的物理意义,且将得到的蠕变参数代入到模型中并不能很好地反映工程实际情况,故需要建立一种简便有效、物理意义明确的蠕变参数确定方法。
基于对岩石蠕变变形阶段的深入分析,通过引入黏弹塑性损伤元件[15]描述加速蠕变,提出一种通过模型方程结合试验数据确定蠕变参数的方法;通过对确定的蠕变参数进行不同应力和不同时间作用下变化规律的分析,将参数模型反代入损伤本构模型中得到模型曲线,并将其与试验曲线进行对比,验证本文提出蠕变参数确定方法的正确性,以进一步完善岩石流变特性的研究方法。
1 岩石蠕变全过程分析通过引入文献[15]的黏弹塑性损伤模型,对原模型的损伤演化方程改进,用以分析不同应力和不同时间双重影响下岩石蠕变全过程。此黏弹塑性模型由Kelvin体(E2)和弹塑性损伤体(E1)组成(图1)。
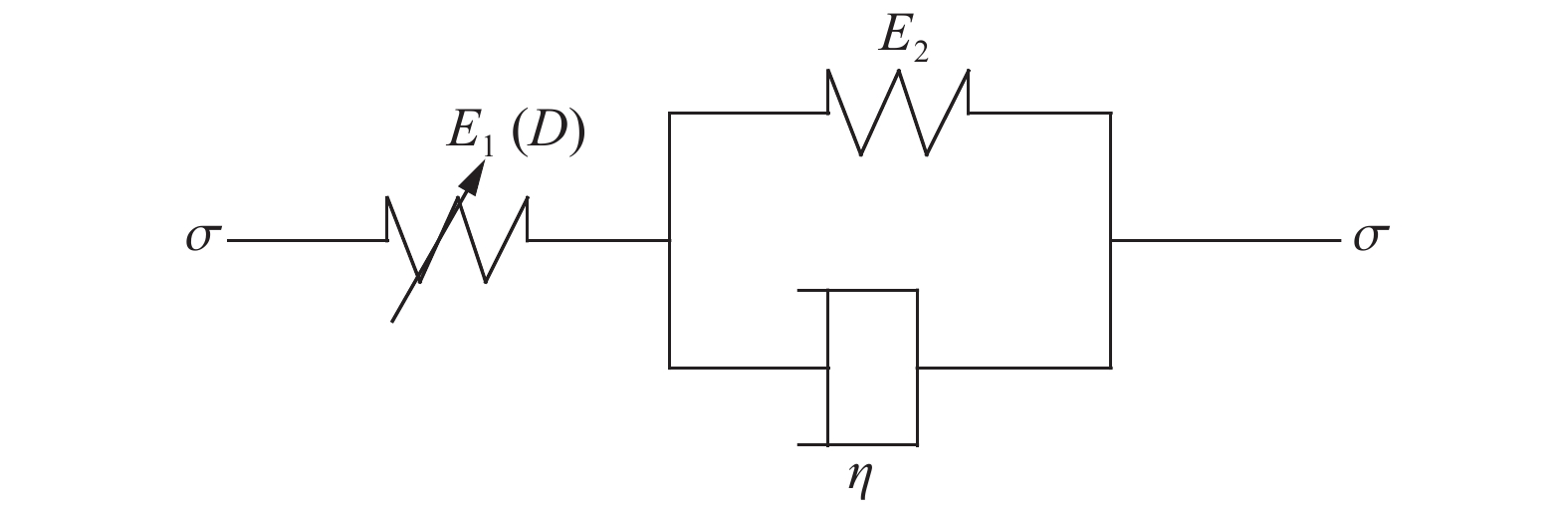 |
| 图1 蠕变模型 Fig. 1 Creep Model |
由于本文试验为假三轴,存在关系σ1>σ2=σ3,则岩石在3维状态下的蠕变模型为:
当σ < σs(σs为屈服应力)时,
| $\begin{aligned}[b] {\varepsilon _1} =& \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}} + \\ &\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_2}}}\left[ {1 - \exp \left( { - \frac{{{G_2}}}{\eta }t} \right)} \right] \end{aligned} $ | (1) |
当σ ≥ σs(σs为屈服应力)时,
| $\begin{aligned}[b] {\varepsilon _1} =& \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right]{\left( {\frac{{{t_{\rm{F}}} - t}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - C}} + \\ &\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_2}}}\left[ {1 - \exp \left( { - \frac{{{G_2}}}{\eta }t} \right)} \right] \end{aligned} $ | (2) |
式(1)~(2)中,ε1为轴向应变,σ1为轴向应力,σ3为围压,G1为弹性体剪切模量,K为体积模量,tF为蠕变破坏时间,
蠕变变形进入加速蠕变阶段后,当t→tF时,岩石轴向应变ε1→∞,且dε1/dt→∞,故式(2)可描述岩石的加速蠕变变形特征。无加速蠕变变形时,可采用式(1)对蠕变曲线进行描述。
2 蠕变模型参数确定为得到蠕变参数的确定方法,需要对蠕变参数的影响因素进行分析,进而改进描述岩石蠕变特性的蠕变本构模型。
2.1 蠕变破坏时间tF和岩石发生加速蠕变的时刻蠕变破坏时间tF为岩石蠕变的全过程历时,即岩石蠕变破坏时对应的蠕变速率趋于无穷大的时刻;岩石发生加速蠕变的时刻
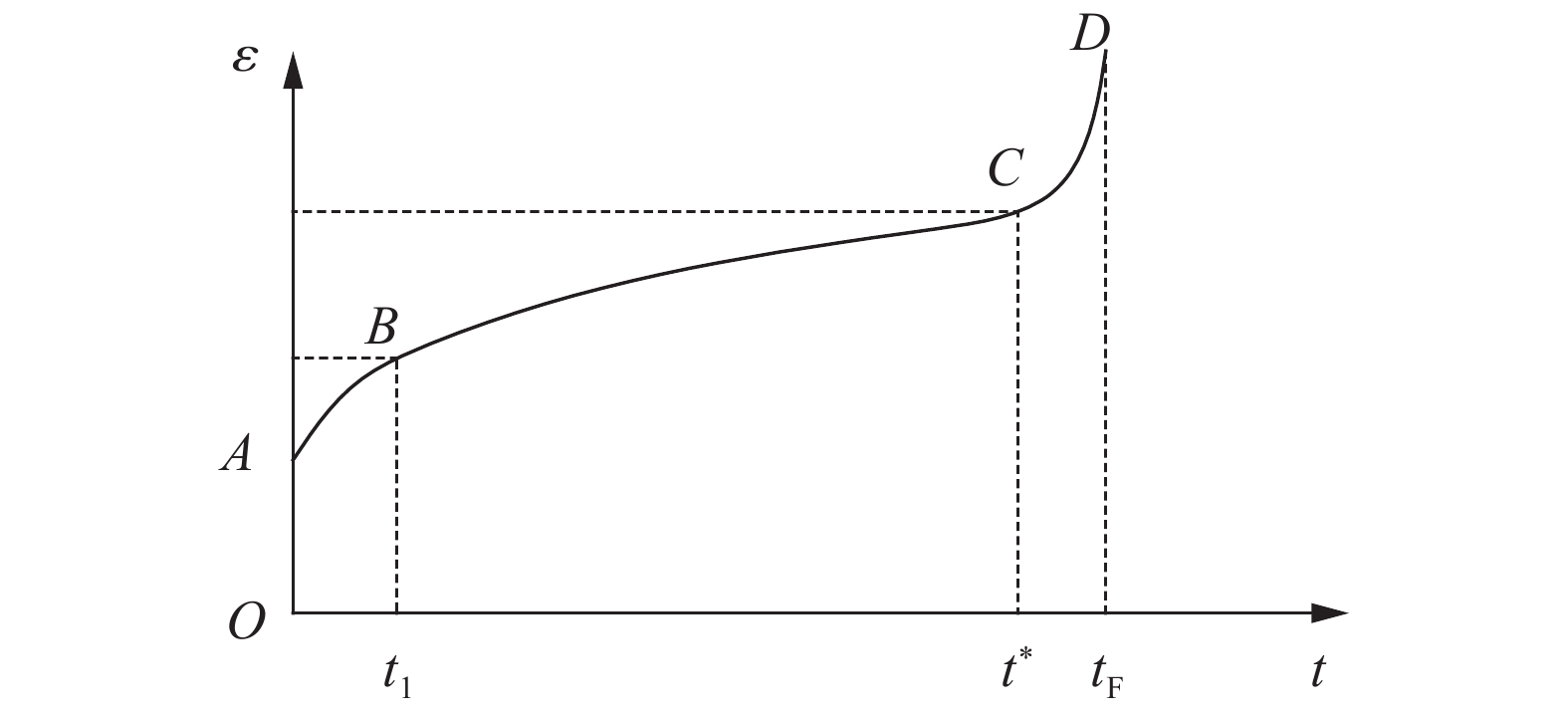 |
| 图2 岩石蠕变曲线 Fig. 2 Rock creep curve |
2.2 剪切模量G1和体积模量K
在岩石蠕变过程中,假设瞬时应变都是弹性应变,则可通过试验曲线的瞬时体积应变值确定各级应力状态下的初始体积模量K0。岩石的初始瞬时应变ε0、剪切模量G1和体积模量K满足式(3),将确定的初始体积模量K0代入式(3)得到岩石的剪切模量G1[17]。
| $\left\{ \begin{array}{l} K = \dfrac{{{\sigma _{\rm{m}}}}}{{3{\varepsilon _{\rm{m}}}}} = \dfrac{{{\sigma _{\rm{m}}}}}{{{\varepsilon _{\rm{v}}}}}, \\ {\varepsilon _0} = \dfrac{{{\sigma _{\rm{m}}}}}{{3K}} + \dfrac{{{S_{ij}}}}{{2{G_1}}} \end{array}\right. $ | (3) |
式中,σm为应力球张量,Sij为应力偏张量,εv为体积应变。
由于岩石的剪切模量G1只受应力状态影响,故不再讨论时间t作用下的参数确定。但体积模量K受时间t的影响,可结合式(3)和试验数据求得体积模量K在各时刻的数值。
2.3 损伤程度影响参数C参数C是影响损伤程度的参数,岩石蠕变损伤与应力和蠕变时间有关,故参数C应为随应力和时间变化的变量。当岩石蠕变变形进入加速蠕变阶段时,黏弹性蠕变变形随着时间变化逐渐趋于稳定,即由损伤蠕变模型可知,岩石总蠕变变形量应为黏弹性蠕变变形稳定值与黏塑性应变之和[18],进而可得岩石的黏弹性蠕变变形稳定值ε1可表示为:
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _1} = \mathop {{\rm{lim}}}\limits_{{\rm{t}} \to \infty } \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_2}}}\left( {1 - {{\rm{e}}^{ - \frac{{{G_2}}}{\eta }t}}} \right)} \right] = \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_{2\infty }}}}$ | (4) |
式中,G2∞为时间t→∞时的剪切模量,是一个稳定值,不受时间t的影响。
在加速蠕变曲线上任取一个时间点ti,假设图1中的蠕变模型参数和参数C在时间ti小范围内随着时间的变化数值保持不变[19];同时,也可在一个时间点ti附近任取一点tj,存在Ci = Cj,则可以得到:
| $\;\;\;\;\;\;\;\;\;{\varepsilon _i} = \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right]{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_i}}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_{2\infty }}}}$ | (5) |
| ${\;\;\;\;\;\varepsilon _j} = \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right]{\left( {\frac{{{t_{\rm{F}}} - {t_j}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_j}}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_{2\infty }}}}$ | (6) |
联立式(5)和(6),相减得到:
| $\begin{aligned}[b] {\varepsilon _i} - {\varepsilon _j} =& \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right] \cdot \\ & \left[ {{{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)}^{ - {C_i}}} - {{\left( {\frac{{{t_{\rm{F}}} - {t_j}}}{{{t_{\rm{F}}} - {t^*}}}} \right)}^{ - {C_i}}}} \right] \end{aligned} $ | (7) |
最终,通过式(7)可确定出不同时刻下的参数Ci。
2.4 黏弹性参数G2和当σ ≥ σs时,根据式(1)在蠕变曲线上任意取一个时间点ti,存在以下关系:
| $\begin{aligned}[b] {\varepsilon _i} =& \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right]{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_i}}} + \\ & \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_{2i}}}}\left[ {1 - \exp \left( { - \frac{{{G_{2i}}}}{{{\eta _i}}}{t_i}} \right)} \right] \end{aligned} $ | (9) |
对式(1)进行时间t的1阶导数求导后,在蠕变曲线上任取一时间点ti得到蠕变速率εi'为:
| $\begin{aligned}[b] {{\varepsilon _i'}} =& \frac{{{C_i}}}{{{t_{\rm{F}}} - {t^*}}}\left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right] \cdot \\ &{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_i} - 1}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{\eta _i}}}\exp \left( { - \frac{{{G_{2i}}}}{{{\eta _i}}}{t_i}} \right) \end{aligned} $ | (9) |
为方便计算,对式(8)和(9)中的指数函数进行泰勒公式展开,得到:
| ${\;\;\;\;\;\;\;\;\;\exp} \left( { - \frac{{{G_{2i}}}}{{{\eta _i}}}{t_i}} \right) = 1 - \frac{{{G_{2i}}}}{{{\eta _i}}}{t_i} + o\left( {t_i^2} \right)$ | (10) |
将展开的指数函数式(10)代入式(8)和(9)中,得到:
| ${\varepsilon _i} = \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right]{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_i}}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{\eta _i}}}{t_i}$ | (11) |
| $\begin{aligned}[b] {{\varepsilon_i '}} =& \frac{{{C_i}}}{{{t_{\rm{F}}} - {t^*}}}\left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K}}} \right] \cdot \\ &{\left( {\frac{{{t_{\rm{F}}} - {t_i}}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - {C_i} - 1}} + \frac{{{\sigma _1} - {\sigma _3}}}{{3{\eta _i}}}\left( {1 - \frac{{{G_{2i}}}}{{{\eta _i}}}{t_i}} \right) \end{aligned} $ | (12) |
联立式(11)和(12),得到不同时刻下的黏弹性参数G2i和ηi为:
| ${\;\;\;\;\;\;\;G_{2i}} = \left\{ {1 - \left[ {\left\{ {{{\varepsilon _i'}} - \frac{{A{C_i}}}{{{t_{\rm{F}}} - {t^*}}} \cdot {B^{ - {C_i} - 1}}} \right\}\frac{{3{\eta _i}}}{{{\sigma _1} - {\sigma _3}}}} \right]} \right\}\frac{{{\eta _i}}}{{{t_i}}}$ | (13) |
| ${\eta _i} = {\left( {{\varepsilon _i} - A{B^{ - {C_i}}}} \right)^{ - 1}}\frac{{{\sigma _1} - {\sigma _3}}}{3}{t_i}$ | (14) |
式(13)和(14)中,参数A和B可表示为
由此得到了所建立的蠕变模型在不同时刻、不同应力作用下的蠕变参数值。
3 室内蠕变试验 3.1 室内三轴压缩试验岩石试样均取自海棠山隧道围岩,为保证试样均一性,岩样均来自同一断面。按照国际岩石力学学会标准将试样加工成高为100 mm、直径为50 mm的标准圆柱形试件,如图3(a)所示;试验系统采用美国MTS813.02试验机(图3(b))进行。该试验系统刚度为7.0×109 N/m,轴向最大应力为1 600 kN,最大围压为70 MPa。
 |
| 图3 试样和试验系统 Fig. 3 Sample and test system |
试验方案如下:采用荷载控制方式进行加载。将围压加载至预定值,保持围压不变的情况下逐渐增加径向应力,直至试样破坏;加载速率统一选用200 N/s,围压分别选取10和20 MPa。试验结束后,每隔5 s保存试验数据。根据上述试验步骤进行试验,通过试验数据绘制不同围压条件下的三轴应力–应变曲线,如图4所示。
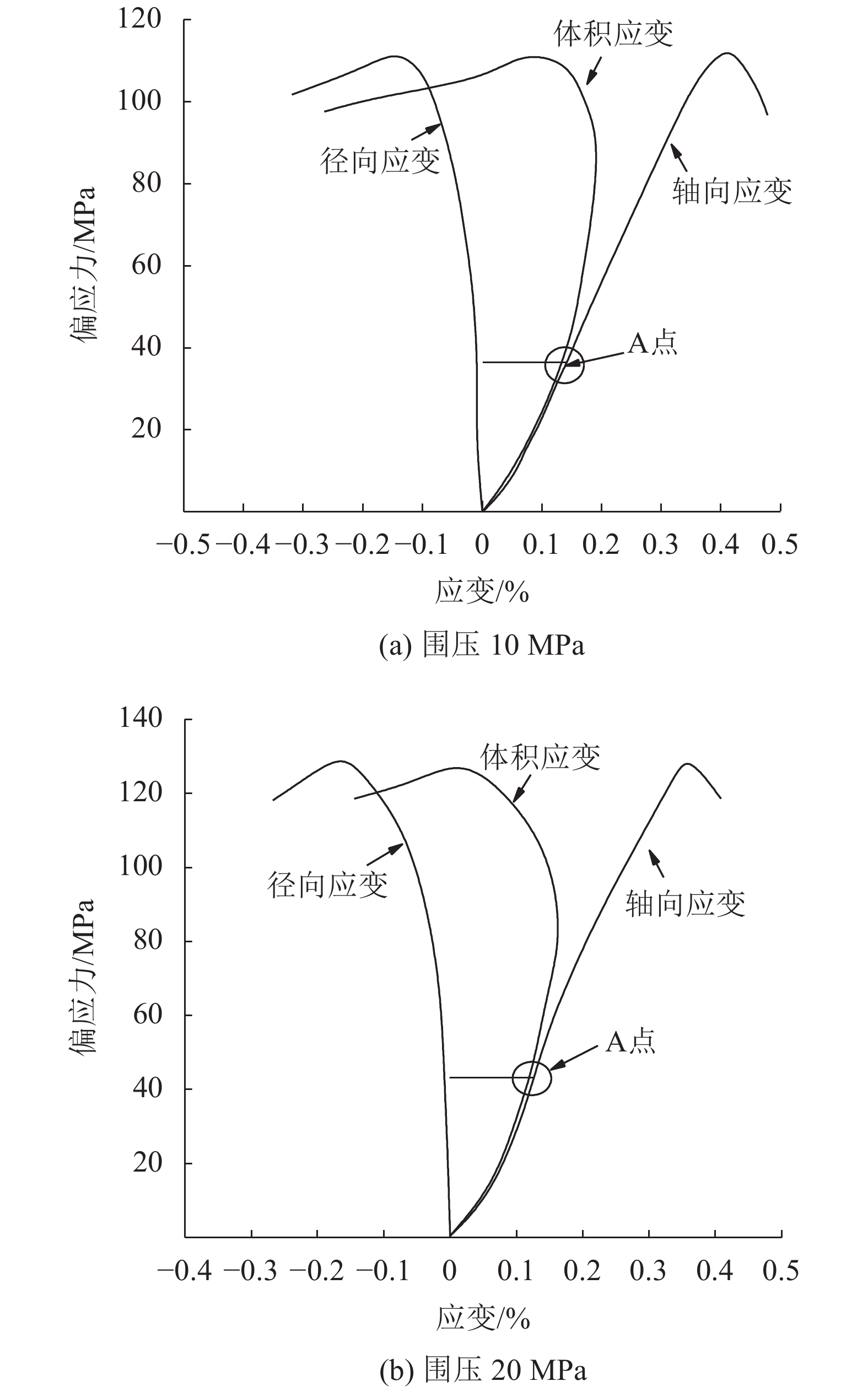 |
| 图4 应力–应变曲线 Fig. 4 Stress–strain curves |
将A点对应的应力作为岩石产生的临界损伤应力[18]。由图4可知,围压10和20 MPa作用下,岩石的临界损伤应力分别为35.27和43.82 MPa。
3.2 蠕变试验方案为研究岩石的流变特性,按照三轴试验中的加载速率施加围压。首先,在施加第1级应力至水平变形稳定后,施加轴向荷载到预定值,并保持恒定,测量和记录岩石试样的轴向应变与时间的关系;然后,按照试验方案逐步进行轴压加载,加载过程必须保证围压恒定。当岩石蠕变进入稳定蠕变阶段或变形稳定阶段(径向变形小于0.03 mm/24 h)时,即可进行下一级轴压的加载,反复至岩石破坏。应力水平取常规三轴压缩试验最大偏应力的50%、60%、70%、80%。
3.3 轴向蠕变结果分析通过陈氏叠加方法[20]对数据进行处理,剔除试验数据异常值,得到不同围压作用下岩石的轴向蠕变变形–时间曲线,如图5所示。
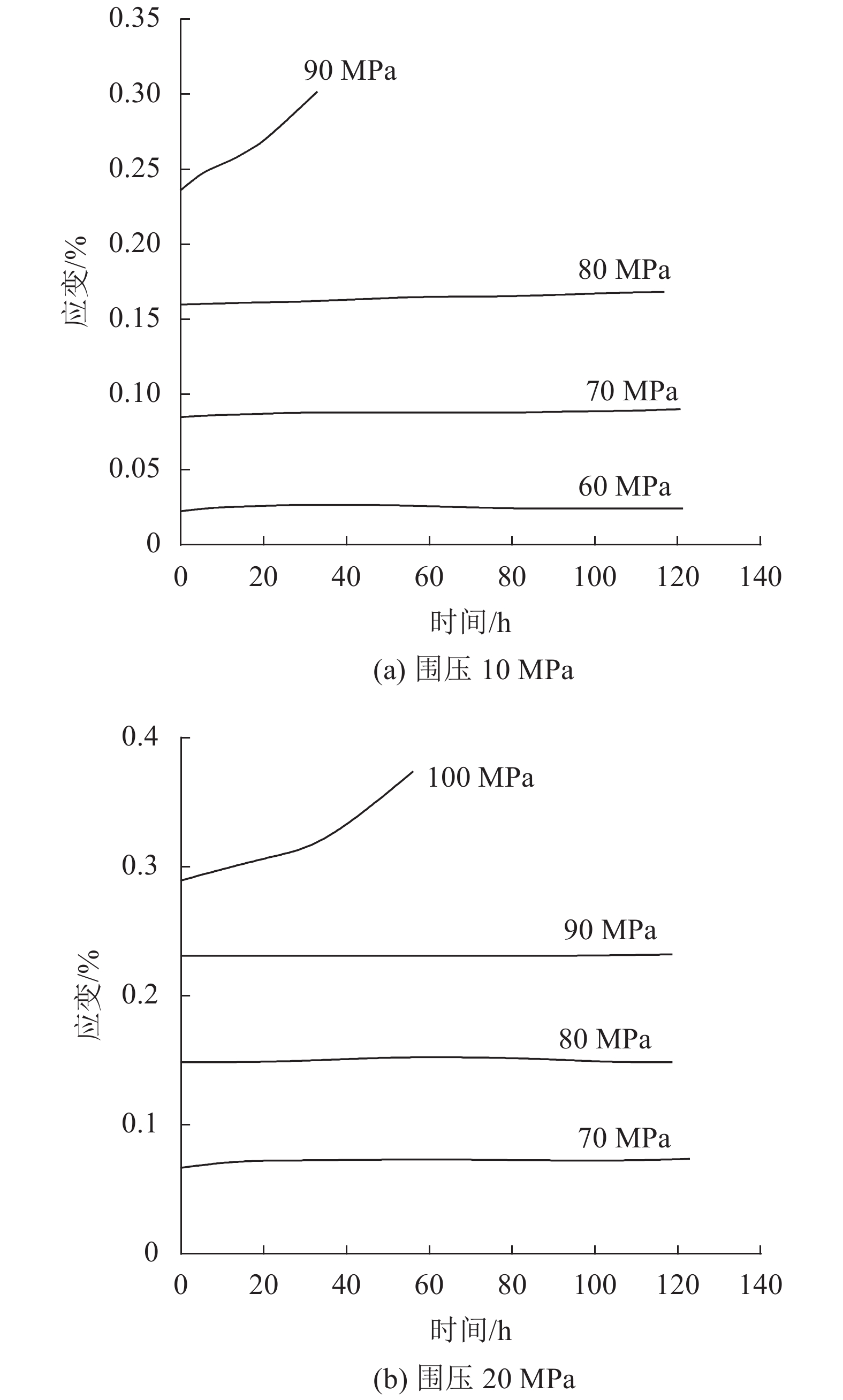 |
| 图5 各级应力下轴向蠕变曲线 Fig. 5 Axial creep curves at all levels of stress |
由图5可知,在蠕变加载初始时刻,不同应力水平下,岩石在加载瞬间都会出现一个瞬时变形,且瞬时变形量随着轴向应力的增大而增大。以围压10 MPa为例:砂岩在低应力水平下(σ3=60 MPa),岩石蠕变变形只是衰减蠕变变形;当应力水平达到一定(σ3=70、80 MPa)时,蠕变变形包括了衰减蠕变和稳定蠕变两种;在高应力水平(σ3=90 MPa)下,出现加速蠕变变形,但加速蠕变变形持续时间较短,岩样随之发生失稳破坏。同时,围压10 MPa时,最后一级应力水平蠕变破坏持续时间大约为32.51 h;围压20 MPa时,最后一级应力水平蠕变破坏持续时间约为55.95 h;围压越大,最后一级破坏持续时间越长,说明围压增大可有效提升岩石的承载力,延长蠕变作用时间。
3.4 蠕变速率结果分析对不同围压作用下的蠕变数据对时间求1阶导数,得到蠕变速率变化规律,如图6所示。
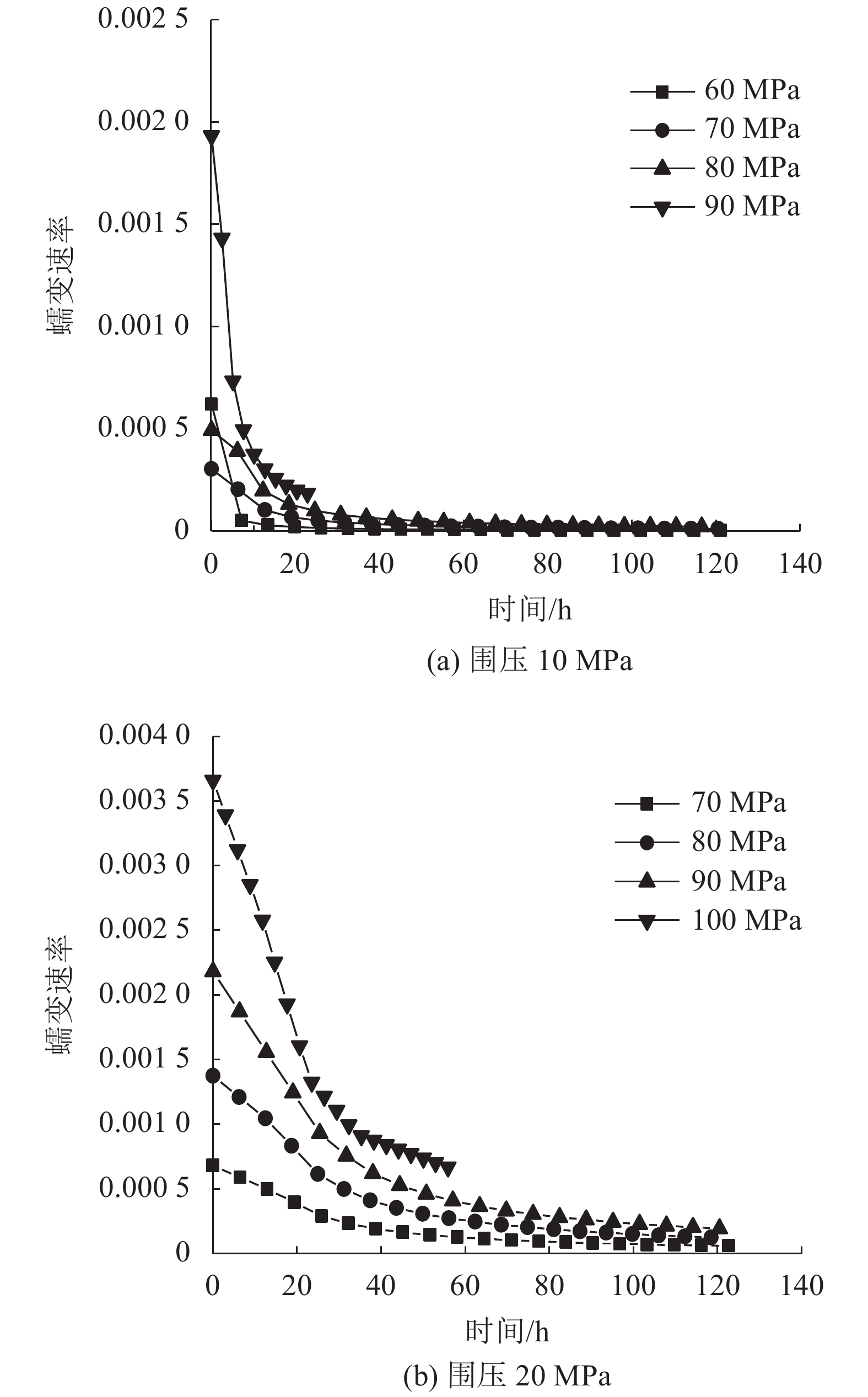 |
| 图6 各级应力下蠕变速率 Fig. 6 Creep strain rate at all levels of stress |
由图6可知:不同应力水平下,均在初始加载瞬间有一个较大的蠕变速率;随后,由于时间推移逐渐减小。以围压10 MPa为例:低应力(σ3=60 MPa)下蠕变速率逐渐衰减至0,此时岩石试样只经历了衰减蠕变阶段;较高应力(σ3=70、80 MPa)下,蠕变速率则趋于一个稳定值,并保持此蠕变速率进入稳定蠕变阶段;更高应力水平(σ3=90 MPa)下,在经历了衰减蠕变和稳定蠕变阶段后,快速进入加速蠕变阶段。
4 蠕变参数变化规律与模型建立 4.1 蠕变参数变化规律分析以围压10 MPa的蠕变试验为例,通过不同时刻蠕变参数的确定方法,得到围压10 MPa时蠕变试验的模型参数见表1。
| 表1 不同时刻下蠕变参数 Tab. 1 Creep parameters at different time |
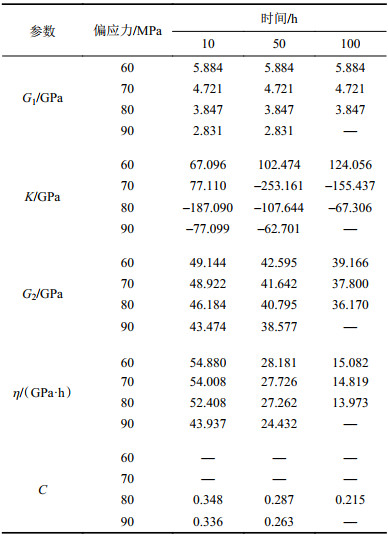 |
根据表1可知,体积模量在过应力差和时间共同作用下会出现负值,难以用数学模型将其变化趋势呈现,故分别讨论在不同过应力差下体积模量K与时间的关系。对体积模量进行数据补充,绘制G1与应力、K与时间的关系,如图7所示。
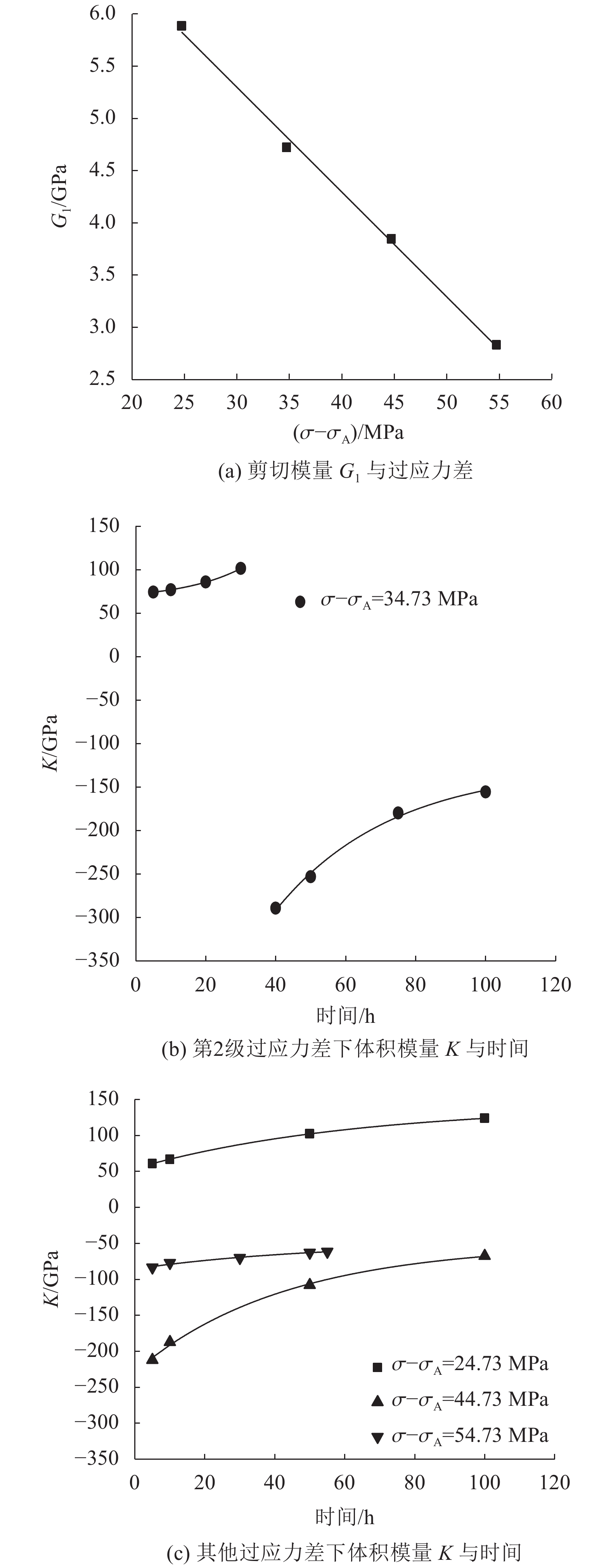 |
| 图7 剪切模量G1与应力及体积模量K与时间的关系 Fig. 7 Relationship between shear modulus G1 and stress, bulk modulus K and time |
剪切模量G1和体积模量K的拟合采用式(15)和(16)。
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_1}\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)} \right] = {a_1} + {b_1}\left( {\sigma - {\sigma _{\rm{A}}}} \right)$ | (15) |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; K\left[\left(\sigma -{\sigma }_{\rm{A}}\right),\;t\right]={a}_{2}{\exp}\left(-t/{b}_{2}\right)+{c}_{2}$ | (16) |
式中,a1、b1、a2、b2、c2均为拟合参数。
由于蠕变参数是随时间和应力变化的变量,岩石的蠕变参数可表示为过应力差和时间的函数,即:
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({G}_{2},\;\eta ,\;C\right)=g\left[\left(\sigma -{\sigma }_{\rm{A}}\right),t\right]$ | (17) |
式中,(σ–σA)为过应力差,g(·)为过应力差与时间的函数。
假设在蠕变过程中,岩石蠕变参数是关于过应力差与时间乘积的函数,即:
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({G}_{2},\;\eta ,\;C\right)=g\left[\left(\sigma -{\sigma }_{\rm{A}}\right)t\right]$ | (18) |
由于蠕变参数在不同应力水平和不同时间作用下具有劣化特征,故可通过蠕变参数的确定方法,结合不同时刻下蠕变变形值和速率值,计算出在不同过应力差和时间乘积作用下的各蠕变参数值(表2)。
| 表2 蠕变参数与(${{\sigma}} -{{\sigma }}_{\bf{A}}$)t关系 Tab. 2 Relationship between creep parameters and (${{\sigma}} - {{\sigma }}_{\bf{A}} $)t |
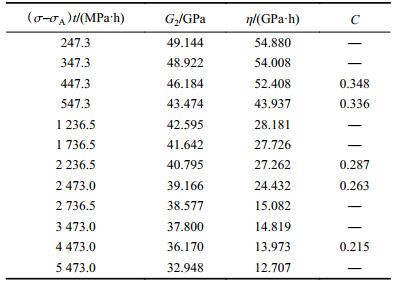 |
蠕变时间取10、50和100 h。绘制蠕变参数与过应力差和时间乘积的关系如图8所示,拟合公式见式(19)。
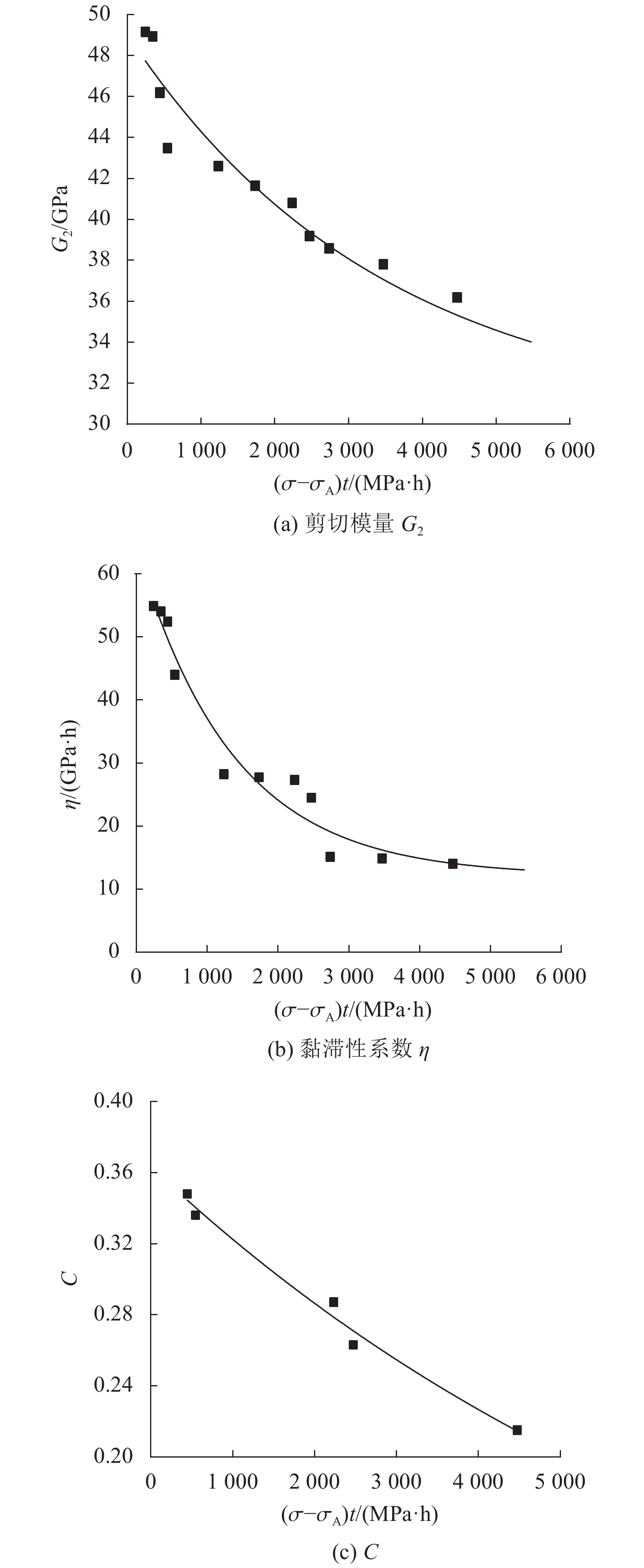 |
| 图8 蠕变参数与过应力差和时间乘积的关系 Fig. 8 Relationship between creep parameters and the product of overstress difference and time |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({G}_{2},\;\eta ,\;C\right)={a}_{i}{\exp}\left[\frac{-\left(\sigma -{\sigma }_{\rm{A}}\right)t}{{b}_{i}}\right]+{c}_{i}$ | (19) |
式中,ai、bi、ci均为拟合参数,i=3,4,5。
由图8可知:根据试验数据,结合蠕变参数确定方法,得出不同(σ–σA)t作用下的剪切模量G1、黏滞性系数η和影响系数C呈指数变化趋势;采用式(19)进行拟合,相关性系数均在0.90以上。同时,得出蠕变参数劣化模型,为后续建立蠕变模型奠定基础。
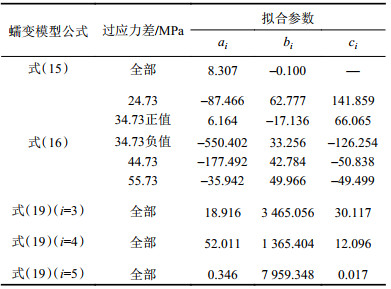
4.2 蠕变模型的改进基于第4.1节蠕变参数与时间和应力的关系,得出蠕变参数模型的拟合参数值见表3,其中,“全部”表示所有过应力差下的模型蠕变参数值。
| 表3 拟合参数 Tab. 3 Fitting parameters |
 |
将式(15)~(19)代入式(1)和(2)中,得到改进后的蠕变模型:
当σ < σs时,
| $\begin{aligned}[b] \varepsilon =& \frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}\left( {\sigma - {\sigma _{\rm{A}}}} \right)}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}} + \\ &\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_2}\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}\left[ {1 - \exp \left( { - \frac{{{G_2}\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}{{\eta \left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}t} \right)} \right] \end{aligned} $ | (20) |
当σ ≥ σs时,
| $\begin{aligned}[b] \varepsilon =& \left[ {\frac{{{\sigma _1} - {\sigma _3}}}{{3{G_1}\left( {\sigma - {\sigma _{\rm{A}}}} \right)}} + \frac{{{\sigma _1} + 2{\sigma _3}}}{{9K\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}} \right] \cdot \\ &{\left( {\frac{{{t_{\rm{F}}} - t}}{{{t_{\rm{F}}} - {t^*}}}} \right)^{ - C\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}} + \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)\left[ {1 - {{\rm{e}}^{ - \frac{{{G_2}\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}{{\eta \left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}}t}}} \right]}}{{3{G_2}\left[ {\left( {\sigma - {\sigma _{\rm{A}}}} \right)t} \right]}} \end{aligned} $ | (21) |
通过式(20)和(21)绘制模型曲线,将其与试验曲线对比,如图9所示。
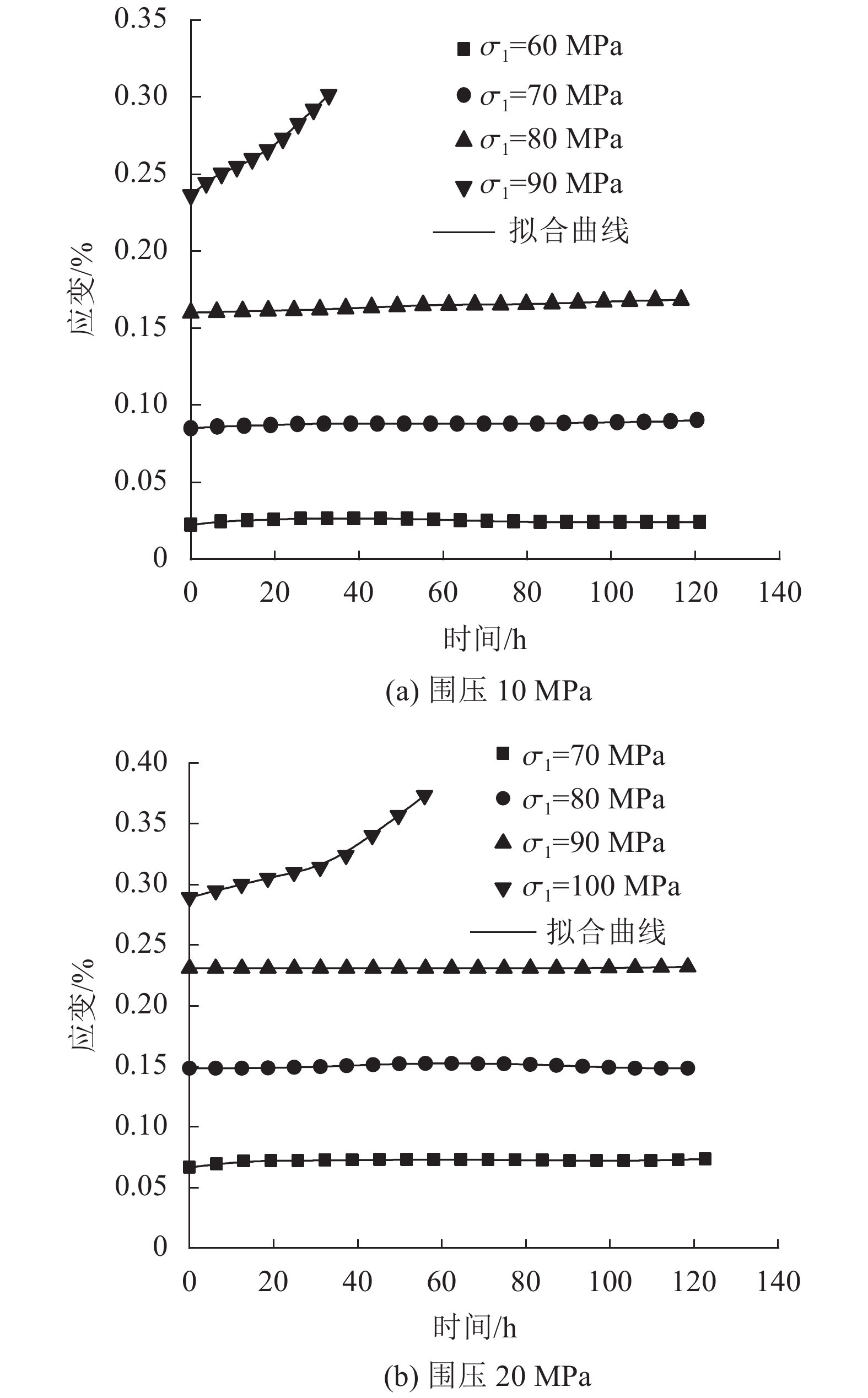 |
| 图9 单试件逐级加载试验数据与模型曲线的对比 Fig. 9 Comparison of the test data of a single specimen with step-by-step loading and the model curves |
由图9可知:本文所建立的考虑时间与过应力差乘积影响的蠕变模型曲线与试验曲线相吻合,较好地描述了岩石衰减蠕变、等速蠕变和加速蠕变的全过程,弥补传统模型难以描述加速蠕变的缺点;同时,引入的损伤模型亦可较好地反映岩石在卸载蠕变过程中的损伤程度。
但文中不同围压作用下蠕变曲线只有在高应力状态下才会出现加速蠕变,为验证模型描述高应力状态下蠕变曲线的可行性,采用文献[10]中单试件、单级加载作用下获得不同应力水平下的蠕变曲线,并将试验曲线与模型曲线进行对比分析,如图10所示。由图10可知,本文提出的改进的蠕变模型考虑了应力和时间的双重影响,能较好地描述岩石在不同应力状态下的蠕变全过程。证明了该模型的正确性与合理性。
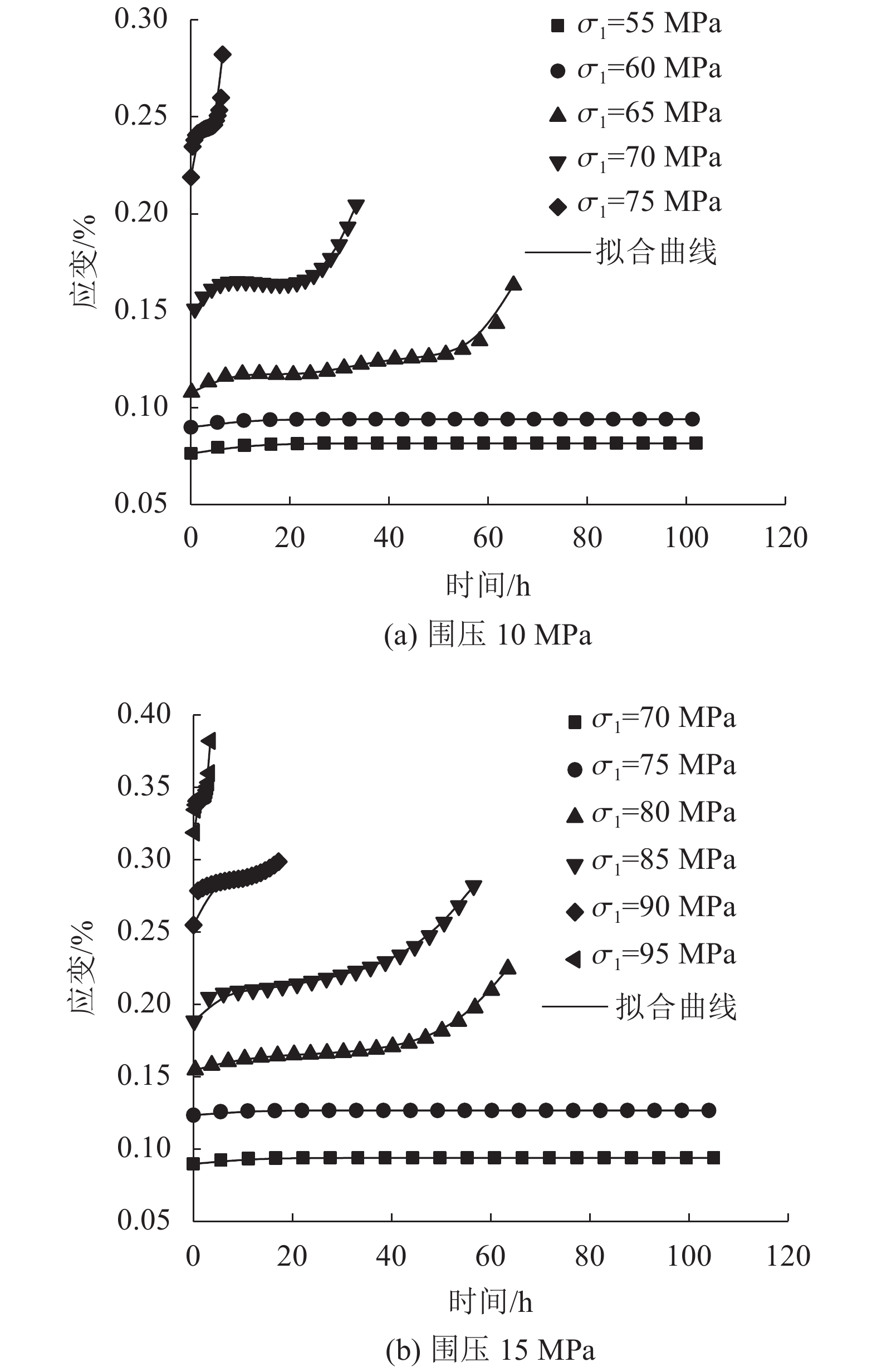 |
| 图10 单试件单级加载试验数据与模型曲线的对比 Fig. 10 Comparison of single-piece single-stage loading test data and model curves |
5 结 论
通过对岩石进行三轴蠕变试验,在对岩石蠕变变形阶段深入分析的基础上,研究了岩石在不同围压条件下的蠕变特性,主要得出以下结论:
1)考虑应力和时间对蠕变参数的双重影响,改进了传统的损伤蠕变模型,并基于试验数据对模型进行了验证。
2)提出确定蠕变参数的方法,得出的蠕变参数具有更明确的物理意义,有助于进一步完善岩石流变的研究方法。
3)分析了蠕变参数随时间和应力差的变化对蠕变的影响,为分析实际工程中岩石的蠕变现象提供了思路。
| [1] |
Zhou M,Song E. A random virtual crack DEM model for creep behavior of rockfill based on the subcritical crack propagation theory[J]. Acta Geotechnica, 2016, 11(4): 827-847. DOI:10.1007/s11440-016-0446-8 |
| [2] |
Chen L,Wang C P,Liu J F,et al. A damage-mechanism-based creep model considering temperature effect in granite[J]. Mechanics Research Communications, 2014, 56(2): 76-82. DOI:10.1016/j.mechrescom.2013.11.009 |
| [3] |
Sih G C. Strain-energy-density factor applied to mixed mode crack problems[J]. International Journal of Fracture, 1974, 10(3): 305-321. DOI:10.1007/bf00035493 |
| [4] |
Zhang Yu,Wang Yaling,Zhang Xiaodong,et al. Experimental study of creep behaviour of gypsum mudstone in a deep reservoir[J]. Rock and Soil Mechanics, 2017, 38(11): 3179-3186. [张玉,王亚玲,张晓东,等. 高埋深储层膏质泥岩蠕变力学特性试验研究[J]. 岩土力学, 2017, 38(11): 3179-3186. DOI:10.16285/j.rsm.2017.11.013] |
| [5] |
Liu Z D. Nonlinear variation parameters creep model of rock and parametric inversion[J]. Geotechnical and Geological Engineering, 2018, 36(5): 2985-2993. DOI:10.1007/s10706-018-0517-8 |
| [6] |
Fahimifar A,Karami M,Fahimifar A. Modifications to an elasto-visco-plastic constitutive model for prediction of creep deformation of rock samples[J]. Soils and Foundations, 2015, 55(6): 1364-1371. DOI:10.1016/j.sandf.2015.10.003 |
| [7] |
Li Yali,Yu Huaichang,Liu Handong. Study of creep constitutive model of silty mudstone under triaxial compression[J]. Rock and Soil Mechanics, 2012, 33(7): 2035-2040. [李亚丽,于怀昌,刘汉东. 三轴压缩下粉砂质泥岩蠕变本构模型研究[J]. 岩土力学, 2012, 33(7): 2035-2040. DOI:10.3969/j.issn.1000-7598.2012.07.018] |
| [8] |
Chen Jing,Jiang Quan,Feng Xiating,et al. Experiment study of time-dependent deformation and failure of original damage marble[J]. Advanced Engineering Science, 2018, 50(5): 27-38. [陈静,江权,冯夏庭,等. 含初始损伤大理岩的时效变形与破坏试验研究[J]. 工程科学与技术, 2018, 50(5): 27-38. DOI:10.1596l/j.jSuese.20l800285] |
| [9] |
Ding Zhikun,Lyu Aizhong. Parameter identification of non-stationary creep equation of rocks[J]. Rock and Soil Mechanics, 2004, 25(Supp1): 37-40. [丁志坤,吕爱钟. 岩石黏弹性非定常蠕变方程的参数识别[J]. 岩土力学, 2004, 25(增刊1): 37-40. DOI:10.3969/j.issn.1000-7598.2004.z1.009] |
| [10] |
Cai Yu,Cao Ping. A non-stationary model for rock creep considering damage based on Burgers model[J]. Rock and Soil Mechanics, 2016, 10(Supp2): 370-374. [蔡煜,曹平. 基于Burgers模型考虑损伤的非定常岩石蠕变模型[J]. 岩土力学, 2016, 10(增刊2): 370-374. DOI:10.16285/j.rsm.2016.S2.047] |
| [11] |
Zhang S,Liu W. The 3D nonstationary creep constitutive model of sandstone based on fractional order[J]. Mathematical Problems in Engineering, 2019(2): 1-12. DOI:10.1155/2019/6031842 |
| [12] |
He Zhilei,Zhu Zhende,Zhu Mingli,et al. An unsteady creep constitutive model based on fractional order derivatives[J]. Rock and Soil Mechanics, 2016, 37(3): 737-744. [何志磊,朱珍德,朱明礼,等. 基于分数阶导数的非定常蠕变本构模型研究[J]. 岩土力学, 2016, 37(3): 737-744. DOI:10.16285/j.rsm.2016.03.016] |
| [13] |
Han Yang,Tan Yuehu,Li Erbing,et al. Non-stationary Burgers creep model of rock and its parameter identification[J]. Engineering Mechanics, 2018, 35(3): 201-217. [韩阳,谭跃虎,李二兵,等. 岩石非定常Burgers蠕变模型及其参数识别[J]. 工程力学, 2018, 35(3): 201-217.] |
| [14] |
Liu Kaiyun,Xue Yongtao,Zhou Hui. A nonlinear viscoelastic-plastic creep model of soft rock with unsteady parameters[J]. Journal of China University of Mining & Technology, 2018, 47(4): 921-928. [刘开云,薛永涛,周辉. 参数非定常的软岩非线性黏弹塑性蠕变模型[J]. 中国矿业大学学报, 2018, 47(4): 921-928. DOI:10.13247/j.cnki.jcumt.000905] |
| [15] |
Cao Wengui,Yuan Jingzhou,Wang Jiangying,et al. A damage simulation technique of the full rock creep process considering accelerated creep[J]. Journal of Hunan University(Natural Science), 2013, 40(2): 15-20. [曹文贵,袁靖周,王江营,等. 考虑加速蠕变的岩石蠕变过程损伤模拟方法[J]. 湖南大学学报(自然科学版), 2013, 40(2): 15-20. DOI:10.3969/j.issn.1674-2974.2013.02.003] |
| [16] |
Kachanov L. Time of the rupture process under creep conditions[J]. Izv. akad. nauk Sssr. otd. tech. nauk, 1958, 8: 26-31. |
| [17] |
Jiang Haifei,Liu Dongyan,Huang Wei,et al. Influence of high pore water pressure on creep properties of rock under high confining pressure[J]. Journal of China Coal Society, 2014, 39(7): 1248-1256. [蒋海飞,刘东燕,黄伟,等. 高围压下高孔隙水压对岩石蠕变特性的影响[J]. 煤炭学报, 2014, 39(7): 1248-1256. DOI:10.13225/j.cnki.jccs.2013.0918] |
| [18] |
Xu Ming,Jin Dehai,Song Erxiang. A rheological model to simulate the shear creep behavior of rockfills considering the influence of stress states[J]. Acta Geotechnica, 2018, 13(6): 1313-1327. DOI:10.1007/s11440-018-0716-8 |
| [19] |
Yan Yan.Research on rock creep tests under seepage flow and variable parameters creep equation[D].Beijing:Tsinghua University,2009. 阎岩.渗流作用下岩石蠕变试验与变参数蠕变方程的研究[D].北京:清华大学,2009. |
| [20] |
Shen Mingrong,Chen Hongju,Zhang Qingzhao. Method for determining long-term strength of discontinuity using shear creep test[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 1-7. [沈明荣,谌洪菊,张清照. 基于蠕变试验的结构面长期强度确定方法[J]. 岩石力学与工程学报, 2012, 31(1): 1-7. DOI:10.3969/j.issn.1000-6915.2012.01.001] |
 2021, Vol. 53
2021, Vol. 53


