2. 四川大学 深地科学与工程教育部重点实验室,四川 成都 610065;
3. 四川大学 破坏力学与工程防灾减灾四川省重点实验室,四川 成都 610065;
4. 同济大学 土木工程学院,上海 200092
2. Key Lab. Deep Underground Sci. and Eng., Ministry of Education, Sichuan Univ., Chengdu 610065, China;
3. Failure Mechanics & Eng. Disaster Prevention and Mitigation, Key Lab. of Sichuan Province, Sichuan Univ., Chengdu 610065, China;
4. College of Civil Eng., Tongji Univ., Shanghai 200092, China
近年来,学者们分析风电塔的可靠性,旨在评估风电塔在不同强度荷载等级下的失效概率,为设计研究以及保险行业提供指导[1]。Nuta等[2] 基于加拿大的抗震反应谱,应用可靠性理论风电塔的抗震分析,对1.65 MW的风电塔进行了易损性抗震风险评估。Patil等[3] 在Nuta等[2]的基础上,对风电塔开展易损性分析,并对近断层地震动与远场地震动进行对比分析。在风–震耦合情况下的风电塔抗震分析中,Asareh等[4]基于美国规范,采用商用有限元软件ABAQUS进行抗震易损性分析。Mo等[5]利用OpenSees对不同运转状态下风机的抗震易损性进行分析。Avossa等[6]采用易损性分析研究方法,对停机和运转工况下抗震失效概率进行对比分析。Fan等[7]基于OpenSees对近断层地震动和远场地震动下的风电塔风–震耦合易损性进行讨论。Yuan等[8]利用全耦合风电塔模型(FAST模型),对风–震耦合易损性进行了多工况下的阐释。Sadowski等[9]虽然没有进行易损性概率转化,但是已经得到了增量时程曲线,并对比了风电塔不同焊缝状态下的地震响应。有研究涉及了抗风易损性分析,Mardfekri等[10]提出了多灾种状态下的风电塔易损性评估框架,基于有限元模型进行抗震易损性和抗风易损性分析,并对灾害发生概率下的可靠度进行了分析。
综上,虽然众多学者已经对风电塔的不同工况、不同结构下的失效概率进行了分析,但绝大部分仅限于抗震易损性研究。对于风电塔而言,由于其固有频率和风荷载接近,风荷载可能更易导致风电塔的破坏。目前报道的倒塌案例[11-13]中,绝大部分是强风荷载下的倒塌,因此风电塔的抗风易损性应当受到重视。另外不同外荷载下风电塔也可能呈现不同的响应和破坏形式[14]。而且,与传统结构的50 a不同,风电塔的设计使用年限为25 a,因此当开展全概率评估时,需要特别考虑由于设计使用年限不同而导致给定时间内灾害的发生概率改变的问题。
基于以上分析,首先以某典型风电塔作为研究对象,对该风电塔设计年限的地震和风的危险性进行分析,然后利用增量时程法对于风电塔的地震易损性和风易损性进行评估,最后根据风电塔设计使用年限内的危险性和易损性分析结果,比较地震和风两种不同灾种下的风电塔失效概率。重点在于两个灾种下风电塔的失效概率对比评估,不考虑风–震耦合下的复杂作用。
1 某典型在役风电塔 1.1 基本信息基于某典型在役风电塔[9,15-18]进行危险性和易损性分析。该风电塔的设计使用年限为25年,建设于上海崇明地区。塔筒总高63.150 m,地面以上1.441 m为刚性基础段,轮毂高度为64.650 m;塔筒底部直径为4.035 m,顶部直径为2.955 m;塔底壁厚为0.250 m,顶部壁厚为0.100 m;风轮半径为35.000 m,轮毂半径为1.750 m;该风电塔的塔架质量为91.000 t,叶片和轮毂的总质量为26.886 t,机舱总质量为60.000 t。塔筒所用的材料为钢材,弹性模量为210 GPa,密度为7 850 kg/m3。
该风电塔的建设地为上海,设防烈度为7度[19],场地的特征周期0.4 s。该场地的10、50和100 a重现期下的基本风压[20]为0.40、0.55和0.60 kN/m2。基于上述场地的相关数据,通过危险性分析换算出符合该风电塔设计使用年限(25年)的超越概率曲线。
1.2 有限元模型为进行易损性分析,建立风电塔的有限元模型如图1所示,在ABAQUS有限元建模中,塔筒使用3D壳单元建立,单元选择S4R类型。集中质量的轮毂和机舱采用刚性耦合至塔顶截面。法兰近似设置为壳单元,并通过增加厚度和质量密度近似反映风电塔法兰对于塔筒质量刚度的突变效应。根据门洞的实际尺寸,对于底部塔段进行切割,并依照实际情况,在门框处使用梁单元进行加固。为了更好地模拟风电的倒塌过程,建模中采取自接触设置(无摩擦硬接触),以准确模拟局部屈曲时材料相互接触的真实状况。叶片采用梁单元分14段,截面使用广义截面定义,匹配实际叶片截面的面积、惯性矩、极惯性矩。风电塔属于钢结构,结构阻尼比取为1%[9]。
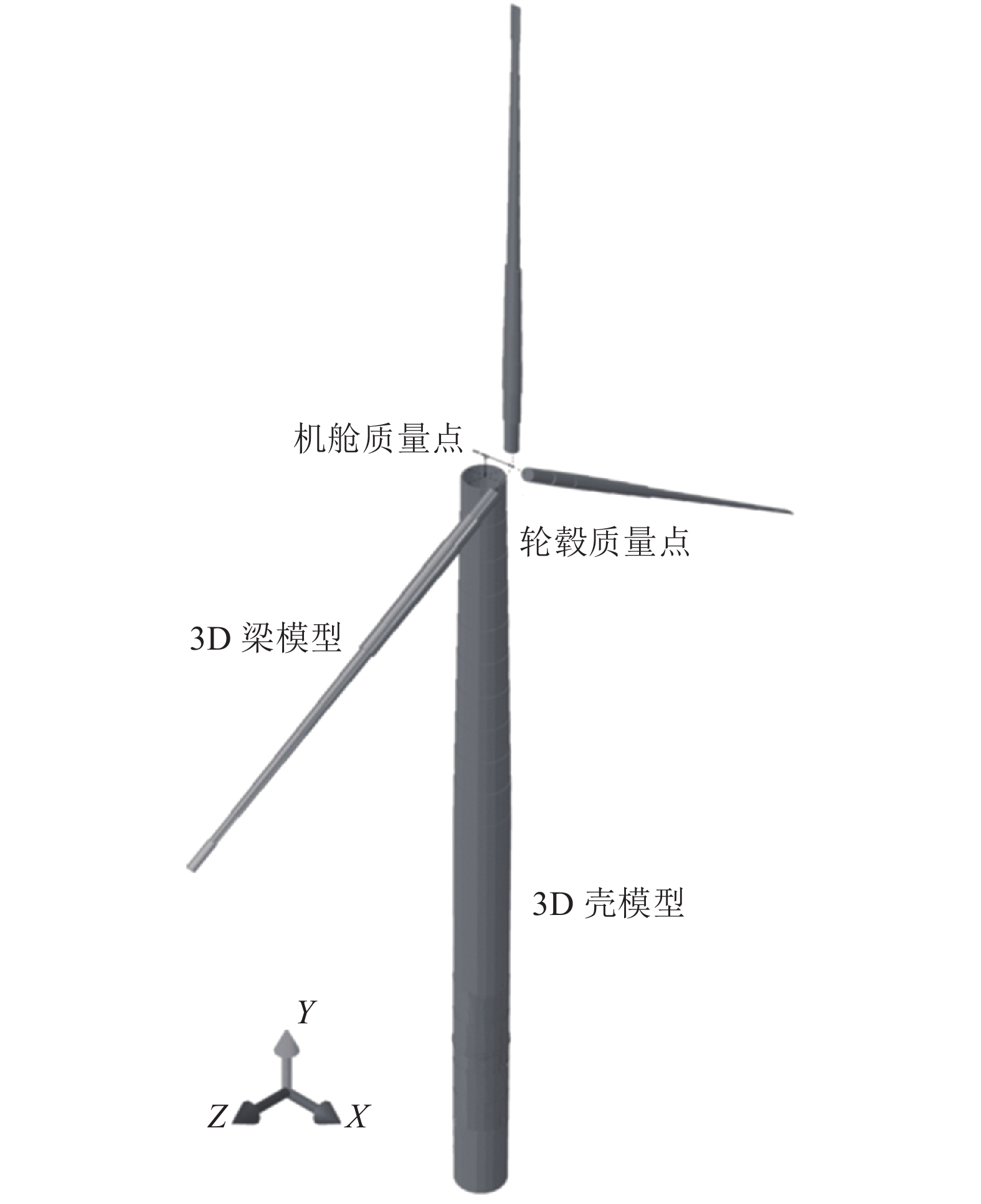 |
| 图1 风电塔有限元模型 Fig. 1 Finite element model of the wind turbine |
通过模态分析,结构的第1频率为0.49 Hz,第2频率为4.38 Hz,与实测值(0.49和3.84 Hz)[17]基本吻合,证明了建模比较准确。结构的前3阶的振型参与系数分别为1.05、0.84、0.35。前3阶的有效质量占比约为70%、15%、6%。风电塔的振型如图2所示。
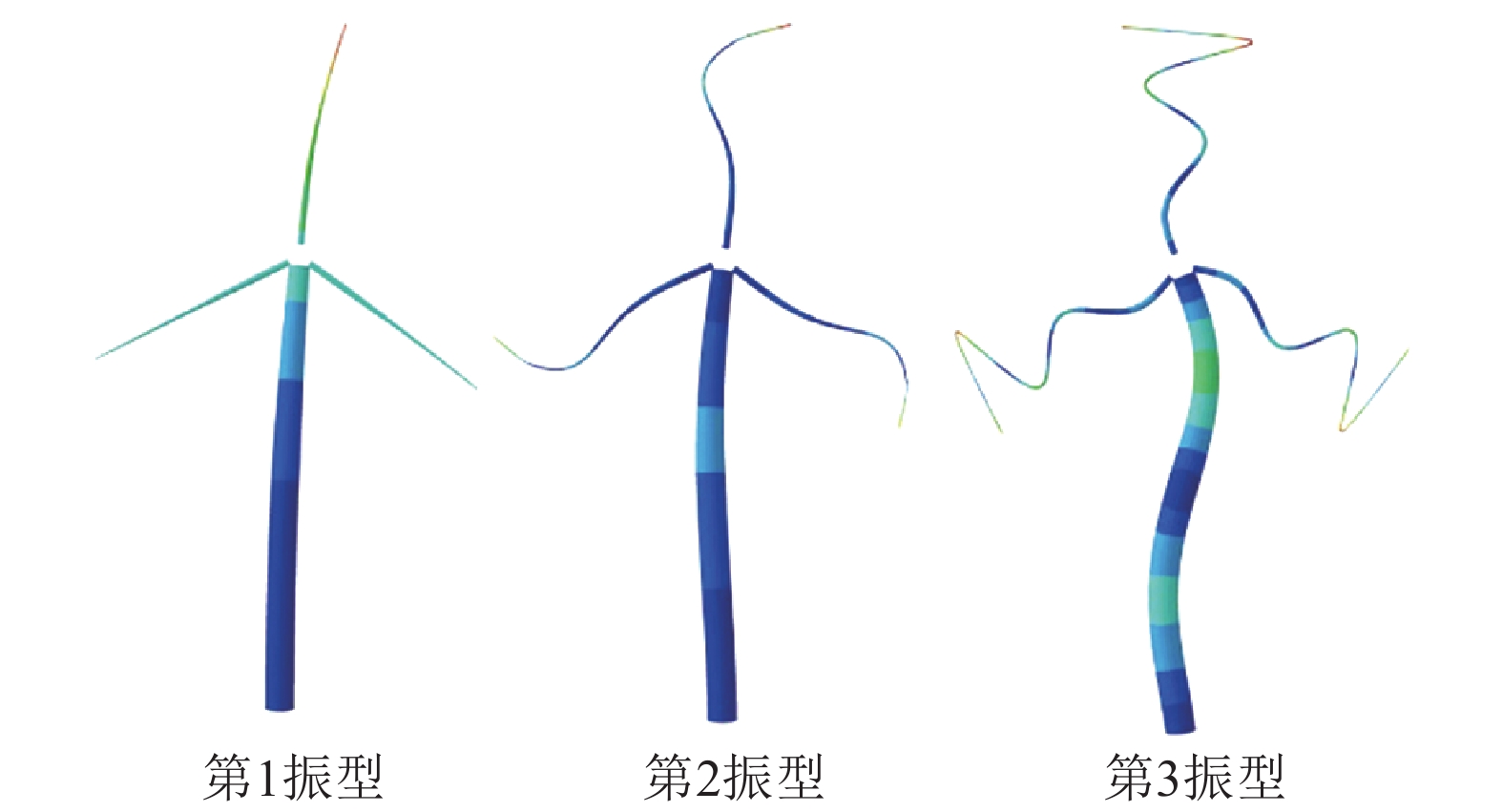 |
| 图2 风电塔振型图 Fig. 2 Structural modes of the wind turbine |
2 灾害危险性分析 2.1 地震危险性分析
地震危险性分析用于评估特定地区发生地震的可能性,中国的抗震规范[19]给定了不同设防烈度下的地震动取值,进而方便设计者进行地震计算。但是规范给定的结构的设计使用年限为50 a,而风电塔结构一般设计使用年限为20至25 a,这意味着若沿用50 a设计使用年限为基准,计算结果偏于保守。所以有必要开展适用于风电塔设计使用年限的地震危险性分析。沈华等[21]探讨了风电塔特有周期下地震动取值分析,使用等超越概率法考虑地震为极值Ⅲ型的概率分布,分别计算不同设计基准期的风电塔地震动的取值。本文应用文献[21]提出的方法,得到了不同地震动强度指标对应的地震发生概率。
为了将设计使用年限由规范给定的50 a调整到25 a做比较,基于上海地区的设防烈度绘制了不同设计使用年限下的曲线图,如图3所示。由图3可以看到,当设计使用年限为50 a时,7度烈度地震的超越概率为10%,符合设防烈度的定义,证明计算无误;设计使用年限越小,发生概率越低,对于特殊设计使用年限较低的结构,例如风电塔结构,使用过高的设计使用年限会使后期抗震计算过于保守。因此,应当采用特定设计使用年限下的地震危险性分析结果。
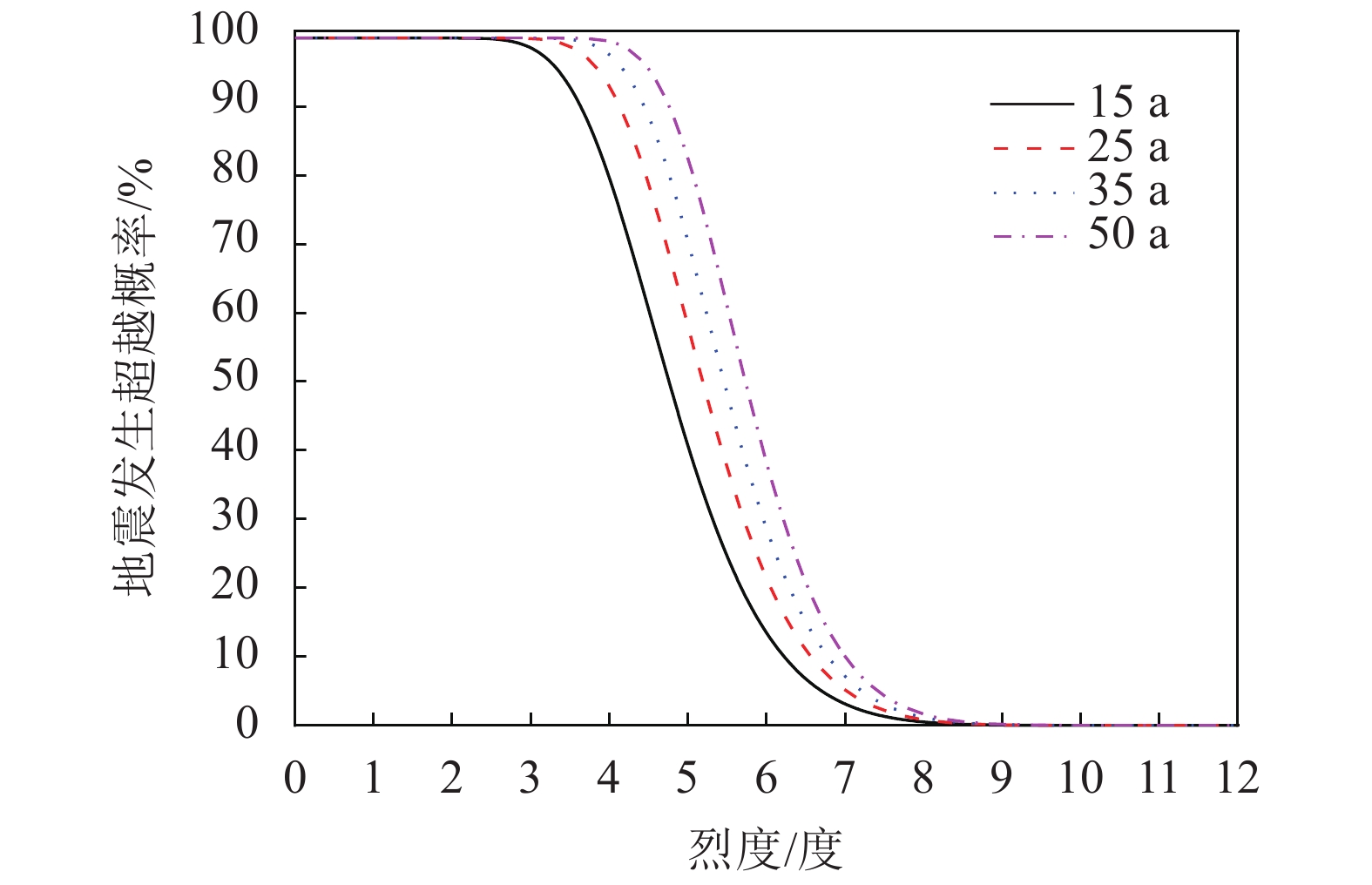 |
| 图3 地震危险性曲线 Fig. 3 Hazard curves for earthquake |
2.2 风危险性分析
风危险性分析是为了求得在给定设计使用年限内风速的超越概率。我国荷载规范[20]规定给定了10、50、100 a重现期下的基本风压取值,并给出了对于不同重现期的换算公式,如式(1)所示:
| ${x_R} = {x_{10}} + ({x_{100}} - {x_{10}})(\ln R/\ln 10 - 1)$ | (1) |
式中,xR为R年重现期的基本风速,x10和x100为10和100 a重现期下的基本风压。
根据式(1)可以推导任意给定风速xR的对应重现期R,进而计算给定年份下的超越概率,变换公式(2)可得:
| $R = \exp \left[ {\bigg(\frac{{{x_R} - {x_{10}}}}{{{x_{100}} - {x_{10}}}} + 1\bigg) \times \ln 10} \right]$ | (2) |
若某一基本风速的重现期为R年,那么每年的不超越概率P1为:
| ${P_1} = 1 - \frac{1}{R}$ | (3) |
则特定设计使用年限t内的风速的超越概率为:
| ${P_t} = 1 - {P_1}^t$ | (4) |
这样,通过给定一系列风速,可以得到设计使用年限内的风速超越概率。
与地震危险性分析类似,对比了不同设计使用年限下的发生概率,如图4所示。由图4可以看到,随着设计使用年限提升,风的发生概率增加,因此对于不同设计使用年限的结构,需要适用于不同的超越概率曲线。
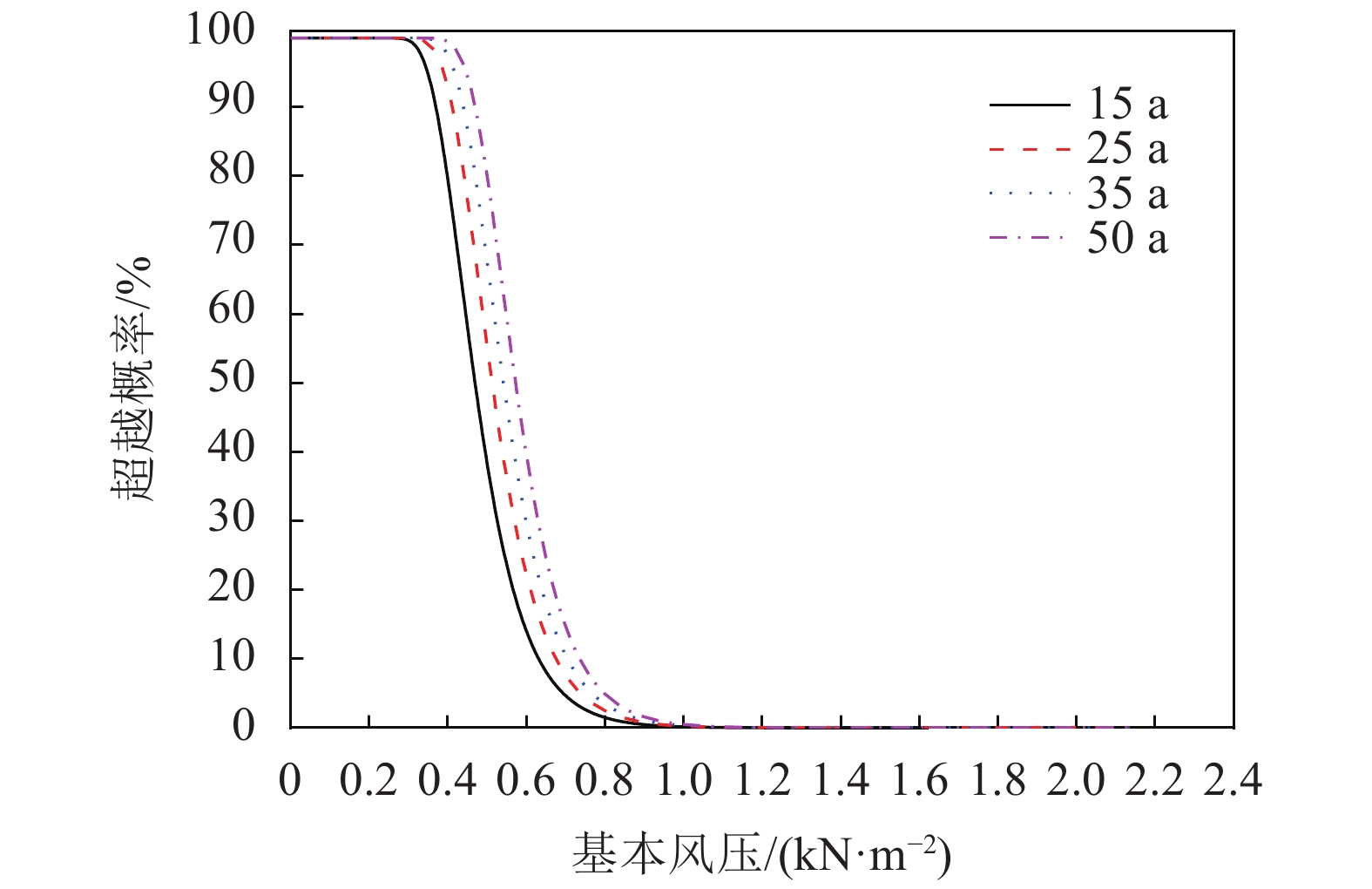 |
| 图4 风危险性曲线 Fig. 4 Hazard curves for wind |
3 结构易损性分析 3.1 增量动力时程分析
利用经典的增量动力时程分析求解结构的抗震易损性的方法应用在风电塔结构的抗震易损性分析中,基本过程如下。
1)建立风电塔的弹塑性分析模型。
2)选择一定数量的地震动记录,定义地震动强度指标和工程需求参数,通过对地震动记录强度设置增量对结构进行非线性时程分析,得到风电塔在不同强度下的动力响应,进而得到IDA曲线簇。
3)定义极限状态,特别对于非线性状态需要合理的量化指标。
4)假定响应服从对数正态分布,可以计算结构的失效概率,如式(5)所示:
| $P(D > {D_L}|{\rm{IM}}) = 1 - \varPhi \bigg(\frac{{\ln ({D_L}) - {\sigma _{\ln (R)}}}}{{{\beta _{\ln (R)}}}}\bigg)$ | (5) |
式中,D为某一工程需求参数响应,DL为极限状态,IM为强度指标,σ 为算数平均值算子,β为标准差算子。
5)以强度指标为横轴,以失效概率为纵轴,绘制抗震易损性曲线。
以上类比,更改地震的强度指标概率为风的强度指标可以得到风易损性曲线。但是值得注意的是,对于风电塔,随着风速不同,风轮的运转状态会不同。轮毂处风速在3~25 m/s范围时,作者所讨论的风电塔处于运转工况,风速超过25 m/s,为了保护风机,风电塔处于停机工况,对于这种较为特殊的结构特点,风易损性分析中应加以考虑。
3.2 地震易损性分析 3.2.1 地震动选波在PEER数据库[22]中基于中国规范中给定的5%阻尼比的加速度反应谱[19]进行地震动调幅选择(图5),共选择了10条地震动进行分析。由于PEER数据库中仅提供5%阻尼比加速度反应谱搜索,因此选波阻尼比与结构阻尼比不一致。为了保证所选地震动在研究风电塔时也具有代表性,通过调幅反算并验证1%阻尼比的反应谱在平均意义下匹配。反应谱的特征周期为0.4 s,在偏硬土场地的情况下,剪切波速没有进行特殊的限制以使拟合精度更好。地震记录以标准误差为基准进行拟合优选。
 |
| 图5 地震动反应谱 Fig. 5 Response spectra of ground motions |
地震动的强度指标的选取,使用反应谱加速度会包含结构自身的特性,但由于地震动有两个水平方向,地震动记录使用平方和开根号的方法来确定地震动强度,如式(6)所示:
| ${S_a}({T_1}) = \sqrt {{S_{a1}}{{({T_1})}^2} + {S_{a2}}{{({T_1})}^2}} $ | (6) |
式中,Sa为反应谱加速度,T1为结构的第1周期。
经过试算,为了使风电塔进入弹塑性范围内,地震的强度采样点为结构基本周期下的谱加速度分别为0.3g、0.6g、0.9g、1.2g、1.5g、1.8g、2.1g、2.4g、2.7g、3.0g。
3.2.2 工程需求参数以及极限状态定义工程需求参数以及极限状态的定义尤为重要,风电塔结构与传统建筑结构不尽相同,在倒塌时会产生屈曲现象,根据目前大多数风电塔易损性研究以及试算,在这里定义了3个需求参数及极限状态。
塔顶位移(极限状态1):风电塔的塔顶位移作为评价风电塔性能的一个重要参数[2-4],被选为风电塔的第1工程需求参数。根据《高耸结构设计规范》[23]位移角不大于1%被认为是正常使用时安全,因此将具有1%的塔顶位移角的塔顶位移(0.65 m)作为第1极限状态,也是风电塔正常使用的极限状态。
Mises应力强度(极限状态2):钢材达到屈服强度进入弹塑性,风塔在此阶段可认为发生不可逆转的破坏。因此,Mises应力强度被选为第2工程需求参数,相应地,钢材的屈服应力355 MPa也被选取为第2极限状态,即屈服极限的界限。
塑性耗能比(极限状态3):塑性耗能比定义[15]动力作用下整体结构的任一时程点,结构的塑性变形耗能与外部动力作用输入功之比。风电塔在形成全截面塑性铰后会发生屈曲破坏并倒塌。通过大量试算,发现塑性耗能比可以较为准确地描述风电塔的倒塌,因此塑性耗能比被选为第3工程需求参数。经过试算,当塑性耗能比大于60%时,风电塔均会发生倒塌,因此,60%的塑性耗能比也被选取为第3极限状态。
3.2.3 结果与讨论图6为风电塔的易损性曲线,即超越极限状态的概率曲线。相较于塔顶位移的极限状态,屈服极限状态超越概率和塑性耗能超越概率上升都较为平缓,表示风电塔进入非线性状态可以通过一定塑性耗能来限制响应。当屈服极限的超越概率提升时,塑性耗能超越概率也随着提升,表示风电塔发生倒塌的概率更大。
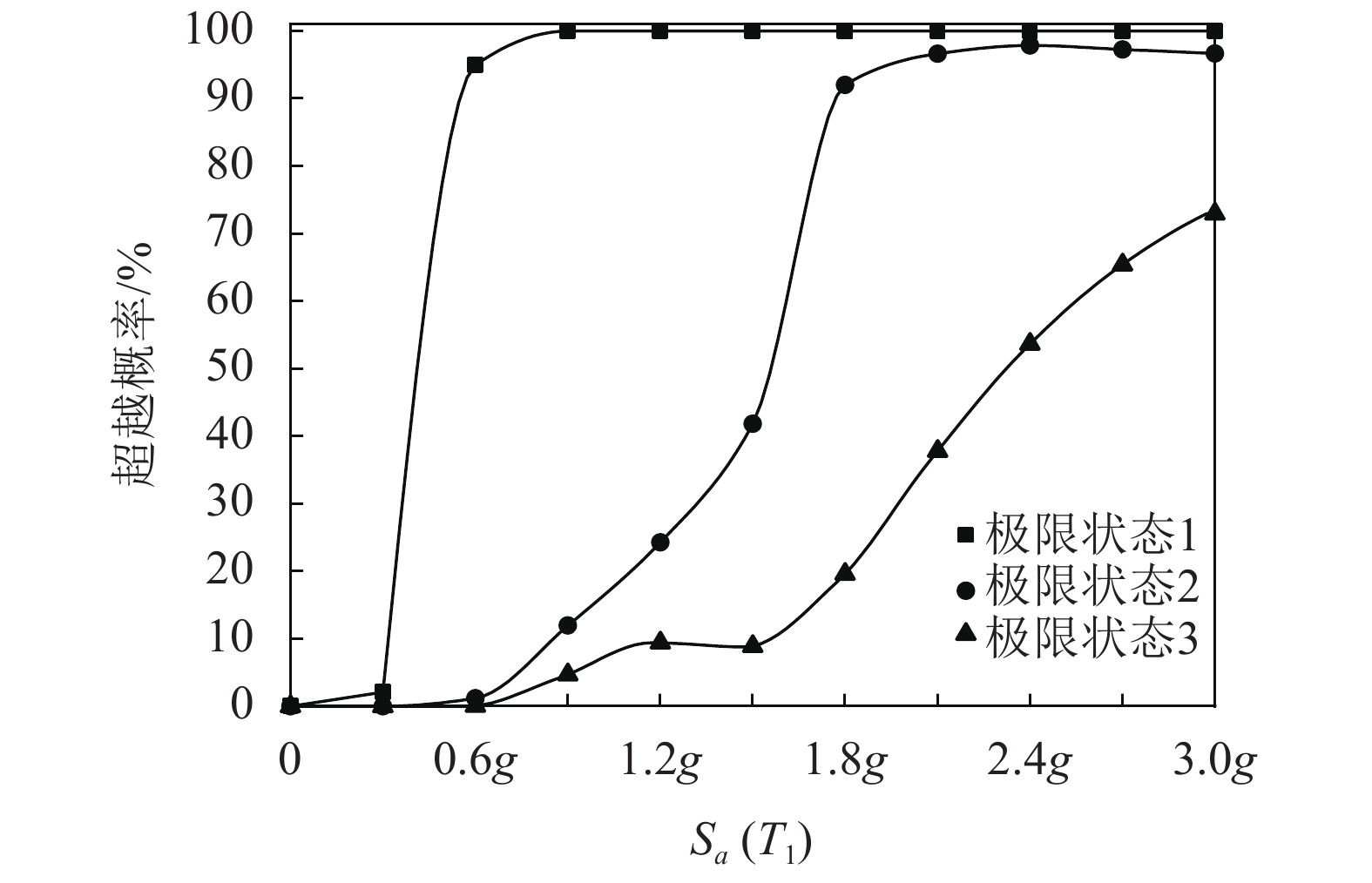 |
| 图6 地震易损性曲线 Fig. 6 Seismic fragility curves |
3.3 风易损性分析 3.3.1 风荷载生成
采用美国可再生能源部(NREL)开发的风机全耦合设计软件FAST和通用有限元软件ABAQUS,来实现风荷载的生成和施加[4,16],具体生成步骤如下:
1)使用FAST常用的前处理软件TurbSim生成风电塔外部风场;
2)为了避免后续再次重复计算塔体动力学效应,在FAST模型刚化塔体后加入该风场进行运转工况下抗风分析;
3)提取顶部的荷载并施加到ABAQUS模型的轮毂位置。
由于风机运转状态会随外部风荷载强度不同而改变,最不利来流风向也会发生相应变化:运转工况下风的入流方向取为前后方向;对于停机工况,根据已有研究[18],风场的流入方向为侧向时为最不利工况,因此停机工况分析中的风向取为侧向。
风谱采用IEC Kaimal谱。脉动风荷载的功率谱对比如图7所示。由图7可以看到,在运转工况下,风电塔在1、2和3 Hz处有峰值出现,因为该风电塔的转速为20 r/min,这3个频率恰好对应这个叶片通过频率的1、2和3倍频,证明运转工况下所选风荷载较为符合实际。另外,无论在停机还是运转工况下,在3~4 Hz范围内均有峰值,这是由叶片自身的局部模态导致的。
 |
| 图7 风荷载的功率谱 Fig. 7 Power spectral densities of wind loads |
对于抗风易损性,风荷载的强度定义为轮毂处平均风速值。在实际风荷载模拟过程中,平均风速会在一定程度上影响脉动风速谱值,因此,实际上随着平均风速值提高,平均风荷载和脉动风荷载均会发生变化。为了使风电塔进入弹塑性范围内,风荷载强度的采样点为轮毂处平均风速分别为5、10、15、20、25、35、45、55、65、75、85 m/s。
3.3.2 工程需求参数以及极限状态定义由于风电塔抗风和抗震研究[9,18]中所关心的需求参数基本一致,因此,易损性分析中的工程需求参数和极限状态与第3.3.1节中相同。
3.3.3 结果与讨论图8为风电塔在风荷载下的IDA曲线簇(极限状态2),可以看到,由于风荷载是使用人工的方法生成的,因此离散性比地震易损性小。另一突出的特点是,在运转工况下,塔顶位移和最大应力经历着一平台段。因为运转工况下,风电塔会不断调整桨距角以维持发电功率,恰好调整的桨距角削弱和降低风荷载。总的来说,风速越高,桨距角越大,受风面积越小,风荷载越小。
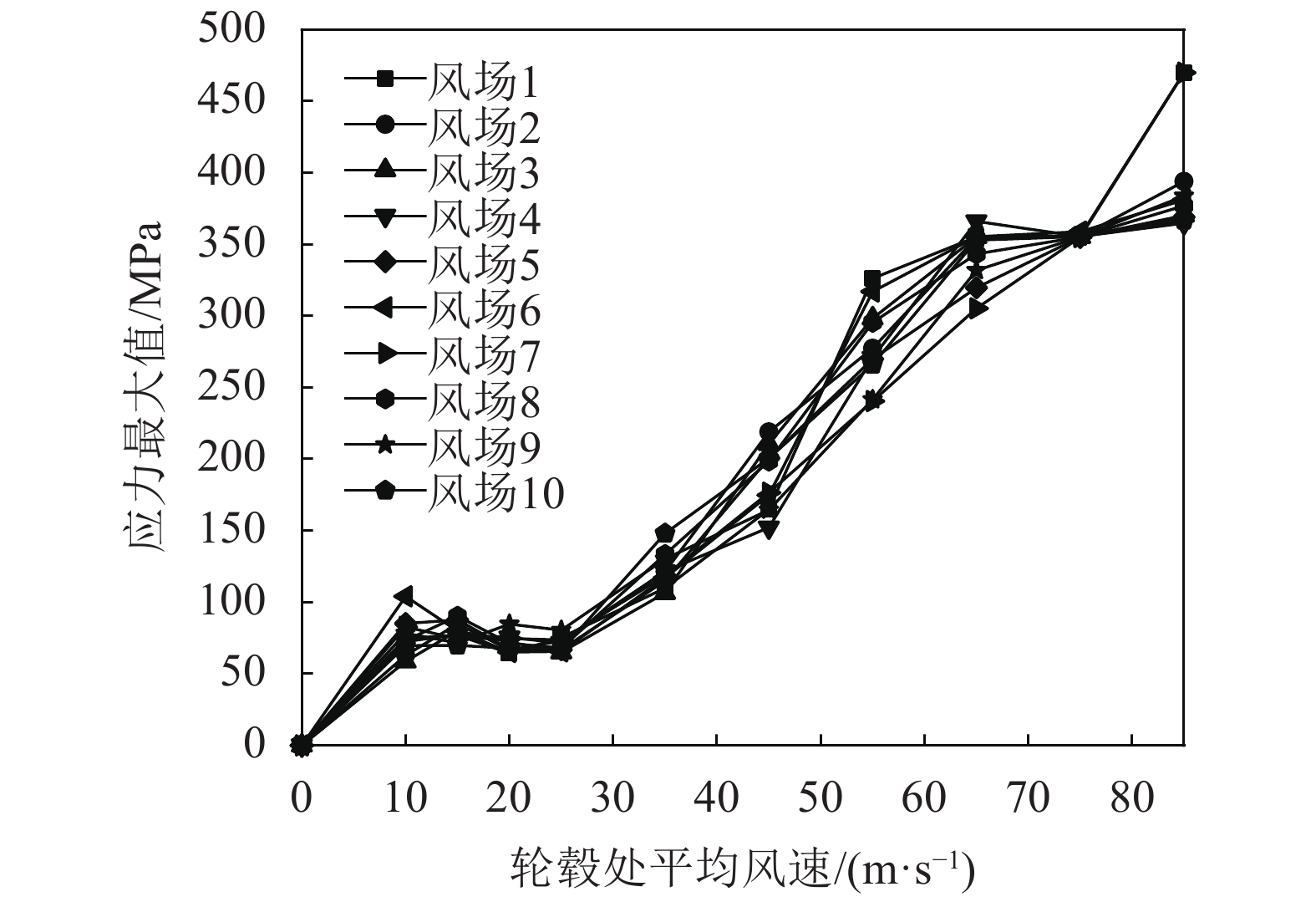 |
| 图8 极限状态2的IDA曲线 Fig. 8 IDA Curves for Limit State 2 |
图9为通过IDA曲线簇计算得到的抗风易损性曲线。与地震易损性类似,塔顶位移具有一定突变型,在此风速56 m/s之后风电塔开始进入塑性状态。需要注意的是,最大应力的易损性曲线趋势在大于65 m/s后有放缓迹象,说明风力发电塔结构塑性发展耗能之后,应力有一定退回的现象[9]。另外,在正常运转下(轮毂风速3~25 m/s),风电塔并不会超越正常使用的极限状态,说明该在役风电塔在运转工况下出现安全问题的可能性较小。
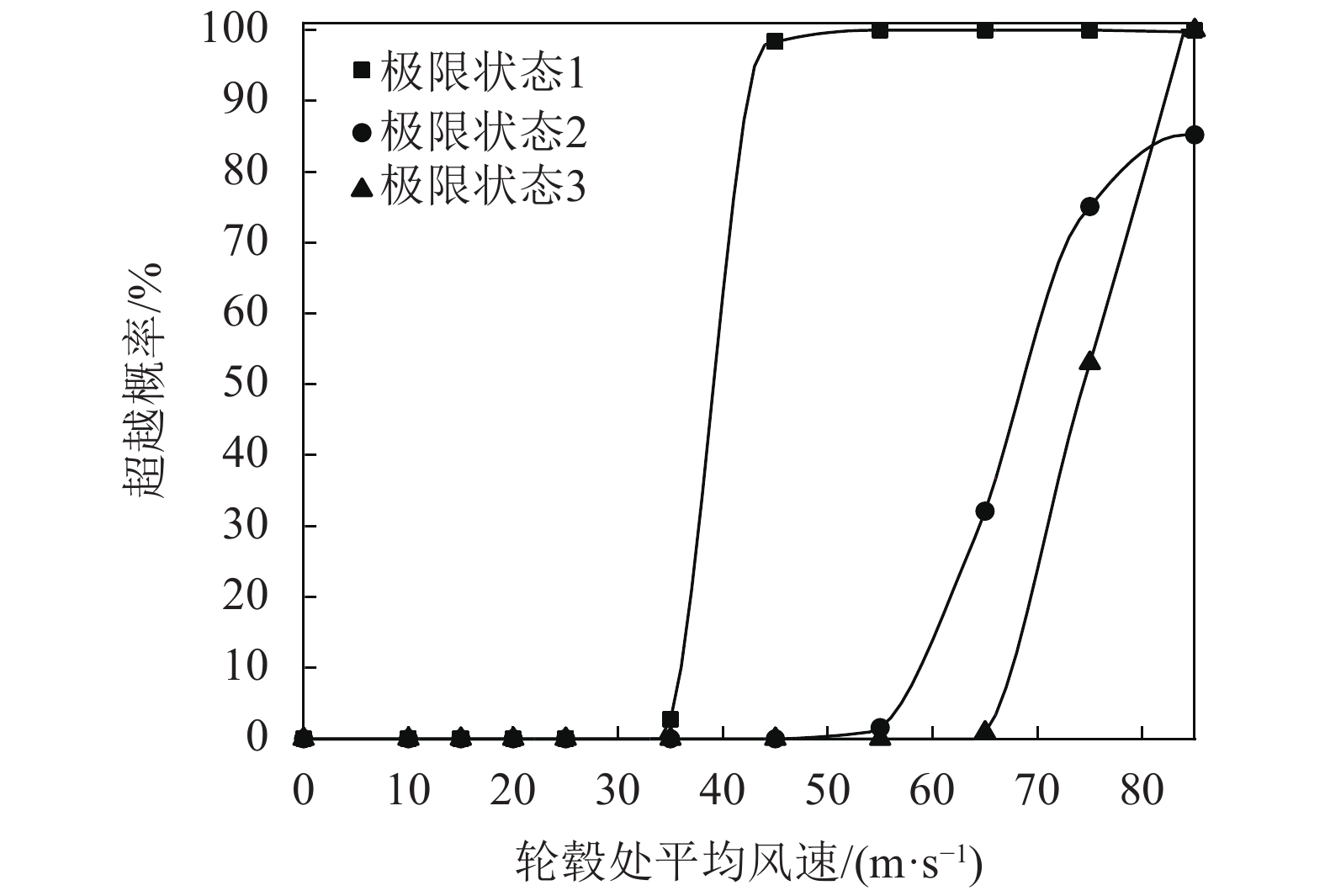 |
| 图9 风易损性曲线 Fig. 9 Fragility curves for wind loads |
4 全概率的对比
对于全概率层面下的失效概率进行了评估。联合危险性分析和易损性分析的全概率求解,可用数学形式表达为:
| $P({L_{\rm{s}}}) = \sum\limits_a {P({L_{\rm{s}}}\left| {A = a} \right.)P(A = a)} $ | (7) |
式中:Ls为极限状态;A为灾害的强度参数;
易损性分析结构可以直接应用在式(7)中,但是危险性分析结构为灾害的超越概率而非发生概率,从概率角度来讲,超越概率曲线为概率分布曲线,然而发生概率曲线为概率密度曲线,因此需要进行转化。概率密度为概率分布的导数,但是考虑到既有的危险性分析曲线为离散数据并非连续函数,因此可以考虑近似有离散差分的方法代替微分,进而求得导数。在这里采用最基本的向前差分的方法,如式(8)所示:
| ${\rm{d}}f(n) \approx f(n) - f(n - 1)$ | (8) |
求得灾害的概率密度曲线后,根据式(7),与易损性曲线相乘求和即可以得到极限状态的发生概率,如表1所示。
| 表1 极限状态的发生概率 Tab. 1 Occurrence probability of limit states |
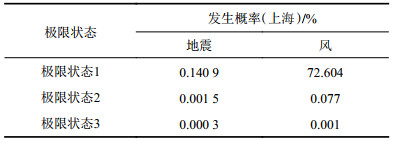 |
从3个不同极限状态来看,极限状态1(正常使用的极限状态)易被超越。这部分概率来源于较高风速的工况,但是在高风速下风电塔会变为停机工况,这时本身风电塔就不会进行运转使用,因此,不会出现结构安全性问题,但会影响风电的持续工作能力。因此极限状态1下的超越概率在本问题中反映了在设计使用年限内,有较大可能因超越正常使用极限而产生风电塔暂停工作的现象,这一现象在风电行业中确实经常发生。屈服和倒塌的极限状态的发生概率较低,但从概率角度来讲也不能排除发生的可能性。
从两个不同灾种的角度来看,地震造成的破坏概率小于风荷载,一方面,因为风电塔是相对长周期的结构,位于反应谱的下降段,因此实际的地震响应较传统结构相比较低,然而风荷载属于相对长周期的荷载,更易激起风电塔的一阶振动;另一方面,风电塔结构一般建设在风能的充沛区域,风荷载的设计强度一般较大,因此更易发生破坏。
5 结论与展望通过地震和风荷载的危险性分析和易损性分析,评估了某典型在役风电塔的失效概率,有如下结论与展望:
1)传统结构的设计使用年限根据规范规定一般为50 a,然而风电塔的设计使用年限一般为25 a,因此,在灾害危险性分析中应该使用针对风电塔设计使用年限的参数,使用过高的设计使用年限进行估计,取值过于保守。
2)风易损性分析中,在风电塔运转工况的风速范围内,随着风速提升,风电塔不断的变桨作用,使结构所受的受风面积减小,总体风荷载近似保持不变,因此在IDA曲线中运转工况范围内有一段平台段。
3)根据在地震和风下的风电塔风险分析,总体来说地震的破坏概率小于风荷载,因为风电塔会建设于风能充沛区,而且其为长周期结构,相比较相对短周期的地震作用,风荷载更易激起结构的振动。
4)对福建等台风、地震均具有较高风险的地区,风电场在风电塔生命周期内存在强风和地震同时发生的可能性,关于风震耦合下的概率化分析将是未来的研究方向。
| [1] |
Dai Kaoshan,Xiao Xue,Liu Kang,et al. Development of earthquake insurance in China and pilot study on its application in wind energy industry[J]. Journal of Natural Disasters, 2018, 27(4): 11-17. [戴靠山,肖雪,刘康,等. 中国地震保险的发展现状分析及其在风电产业应用初探[J]. 自然灾害学报, 2018, 27(4): 11-17. DOI:10.13577/j.jnd.2018.0402] |
| [2] |
Nuta E,Christopoulos C,Packer J A. Methodology for seismic risk assessment for tubular steel wind turbine towers:application to Canadian seismic environment[J]. Canadian Journal of Civil Engineering, 2011, 38(3): 293-304. DOI:10.1139/L11-002 |
| [3] |
Patil A,Jung S,Kwon O S. Structural performance of a parked wind turbine tower subjected to strong ground motions[J]. Engineering Structures, 2016, 120: 92-102. DOI:10.1016/j.engstruct.2016.04.020 |
| [4] |
Asareh M A,Schonberg W,Volz J. Fragility analysis of a 5-MW NREL wind turbine considering aero-elastic and seismic interaction using finite element method[J]. Finite Elements in Analysis and Design, 2016, 120: 57-67. DOI:10.1016/j.finel.2016.06.006 |
| [5] |
Mo R,Kang H,Li M,et al. Seismic fragility analysis of monopile offshore wind turbines under different operational conditions[J]. Energies, 2017, 10(7): 1037. DOI:10.3390/en10071037 |
| [6] |
Avossa A,Demartino C,Contestabile P,et al. Some results on the vulnerability assessment of HAWTs subjected to wind and seismic actions[J]. Sustainability, 2017, 9(9): 1525. DOI:10.3390/su9091525 |
| [7] |
Fan J,Li Q,Zhang Y. Collapse analysis of wind turbine tower under the coupled effects of wind and near-field earthquake[J]. Wind Energy, 2019, 22(3): 407-419. DOI:10.1002/we.2294 |
| [8] |
Yuan C,Chen J,Li J,et al. Fragility analysis of large-scale wind turbines under the combination of seismic and aerodynamic loads[J]. Renewable Energy, 2017, 113: 1122-1134. DOI:10.1016/j.renene.2017.06.068 |
| [9] |
Sadowski A J,Camara A,Málaga–Chuquitaype C,et al. Seismic analysis of a tall metal wind turbine support tower with realistic geometric imperfections[J]. Earthquake Engineering & Structural Dynamics, 2017, 46(2): 201-219. DOI:10.1002/eqe.2785 |
| [10] |
Mardfekri M,Gardoni P. Multi-hazard reliability assessment of offshore wind turbines[J]. Wind Energy, 2015, 18(8): 1433-1450. DOI:10.1002/we.1768 |
| [11] |
Chou J S,Tu W T. Failure analysis and risk management of a collapsed large wind turbine tower[J]. Engineering Failure Analysis, 2011, 18(1): 295-313. DOI:10.1016/j.engfailanal.2010.09.008 |
| [12] |
Chen X,Li C,Xu J. Failure investigation on a coastal wind farm damaged by super typhoon:A forensic engineering study[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147: 132-142. DOI:10.1016/j.jweia.2015.10.007 |
| [13] |
Chen X,Xu J Z. Structural failure analysis of wind turbines impacted by super typhoon Usagi[J]. Engineering Failure Analysis, 2016, 60: 391-404. DOI:10.1016/j.engfailanal.2015.11.028 |
| [14] |
Dai Kaoshan,Mao Zhenxi,Zhao Zhi,et al. Shaking table test study on seismic responses of a wind turbine under ground motions with different spectral characteristics[J]. Advanced Engineering Sciences, 2018, 50(3): 125-133. [戴靠山,毛振西,赵志,等. 不同频谱特性地震动下某风电塔响应振动台试验研究[J]. 工程科学与技术, 2018, 50(3): 125-133. DOI:10.15961/j.jsuese.201800369] |
| [15] |
Zhao Z,Dai K,Camara A,et al. Wind turbine tower failure modes under seismic and wind loads[J]. Journal of Performance of Constructed Facilities, 2019, 33(2): 04019015. DOI:10.1061/(ASCE)CF.1943-5509.0001279 |
| [16] |
Dai Kaoshan,Zhao Zhi,Yi Zhengxiang,et al. Seismic analyses of wind turbine tower under operational conditions[J]. Chinese Journal of Engineering, 2017, 39(10): 1596-1605. [戴靠山,赵志,易正翔,等. 运转工况下风电塔抗震分析[J]. 工程科学学报, 2017, 39(10): 1596-1605. DOI:10.13374/j.issn2095-9389.2017.10.020] |
| [17] |
Dai K,Huang Y,Gong C,et al. Rapid seismic analysis methodology for in-service wind turbine towers[J]. Earthquake Engineering and Engineering Vibration, 2015, 14(3): 539-548. DOI:10.1007/s11803-015-0043-0 |
| [18] |
Dai K,Sheng C,Zhao Z,et al. Nonlinear response history analysis and collapse mode study of a wind turbine tower subjected to tropical cyclonic winds[J]. Wind and Structures, 2017, 25(1): 79-100. DOI:10.12989/was.2017.25.1.079 |
| [19] |
中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB 50011—2010[S].北京:中国建筑工业出版社,2010.
|
| [20] |
中华人民共和国住房和城乡建设部.建筑结构荷载规范:GB 50009—2012[S].北京:中国建筑工业出版社,2012.
|
| [21] |
Shen Hua,Dai Kaoshan,Weng Dagen. Seismic loading for wind turbine tower strucutrual design[J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(3): 84-91. [沈华,戴靠山,翁大根. 风电塔结构抗震设计的地震作用取值研究[J]. 地震工程与工程振动, 2016, 36(3): 84-91. DOI:10.13197/j.eeev.2016.03.84.shenh.011] |
| [22] |
Ancheta T,Darragh R,Stewart J,et al.PEER NGA-West2 Database[R].Berkeley:Pacific Earthquake Engineering Research Center,2013.
|
| [23] |
上海市建设和交通委员会.高耸结构设计规范:GB 50135—2006[S].北京:中国计划出版社,2006.
|
 2021, Vol. 53
2021, Vol. 53


