滚珠丝杠副具有传动精度高、同步性能好、传动效率高等优良性能，已成为航空、航天、石油钻井和科学测量仪器等行业所必需的部件^[1]。在滚珠丝杠副的运行过程中，滚珠与滚道的摩擦和磨损，会降低其精度的稳定性和使用寿命。

滚珠丝杠副中滚珠与螺母或丝杠滚道之间产生的接触应力分析、表面变形以及微观接触特性是滚珠丝杠副摩擦学研究的基本问题。这些问题对滚珠丝杠副的磨损分析、疲劳寿命分析以及滚珠运动状态分析具有重要意义。国内外许多学者对滚珠丝杠副的弹性变形和接触应力进行了深入研究。刘畅等^[2]对滚珠丝杠副的接触变形进行了原理性阐述，建立了两个粗糙的曲面之间的接触多尺度力学模型。Liu等^[3]建立了考虑弹性、弹塑性、塑性变形的表面微凸体接触等接触参数来计算总实际接触面积和接触载荷。Zhao等^[4]在考虑滚珠几何误差的情况下，使用运动分析方法计算了载荷分布和轴向弹性变形。胡建忠等^[5]采用赫兹接触理论建立了滚珠丝杠副轴向接触刚度计算模型。Wei^[6]、Verl^[7]等基于描述滚珠丝杠副接触状态的赫兹理论，对高速滚珠丝杠副进行磨损分析。Chen等^[8]研究了影响滚珠丝杠副轴向接触刚度的各个要素，分别对单螺母弹性变形和轴向刚度进行分析。

以上学者普遍采用赫兹接触理论来对各种接触情况进行近似分析。但是，在滚珠丝杠副中，接触区域是由公称半径、滚道形状、螺旋升角、滚珠半径等共同决定的。由于丝杠滚道和螺母滚道具有螺旋升角，从而造成滚道截面形状的非对称性，且螺旋升角越大导致的非对称性越严重，因此采用Hertz接触理论会造成较大的误差。

为了便于对一般3维型面两接触体之间进行精确的摩擦磨损分析和疲劳寿命分析，国内外许多专家根据最小余能原理和共轭梯度法（conjugate gradient method，CGM）^[9-10]，采用半解析法对一般接触问题进行了深入研究。Kubo^[11]、Francis^[12]等提出利用最小余能原理计算弹性接触中的压力分布和应力分布，这种方法的优点在于可适用于不规则接触表面的接触力学分析。Wang等^[13]基于最小余能方程求解干接触问题，接触压力和切向应力使用共轭梯度法求解，通过解析法得到影响系数，由此计算表面变形或位移，并采用快速傅里叶变换（fast Fourier transform，FFT）加速表面变形的计算^[14]。Ai等^[15]采用半解析法进行粗糙表面的接触问题分析。因此，作者基于最小余能原理的半解析法来求解高速滚珠丝杠副滚珠与滚道之间接触应力分布，使计算结果更加精确。

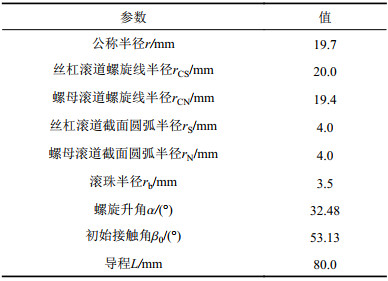
滚珠丝杠副的接触区域的几何形状是由公称半径、滚道截面圆弧半径、螺旋升角、接触角以及滚珠直径等参数共同决定的。计算中所用大导程滚珠丝杠副来源于NSK的产品手册，其各项参数如表1所示。

表1(Tab. 1)

表1 滚珠丝杠副结构参数 Tab. 1 Structural parameters of ball screw mechanism

表1 滚珠丝杠副结构参数 Tab. 1 Structural parameters of ball screw mechanism 参数 值 公称半径r/mm 19.7 丝杠滚道螺旋线半径rCS/mm 20.0 螺母滚道螺旋线半径rCN/mm 19.4 丝杠滚道截面圆弧半径rS/mm 4.0 螺母滚道截面圆弧半径rN/mm 4.0 滚珠半径rb/mm 3.5 螺旋升角α/(°) 32.48 初始接触角β0/(°) 53.13 导程L/mm 80.0

为了对滚珠丝杠副进行运动学分析，首先需要建立滚珠丝杠副系统的坐标系^[15]，如图1所示。分别在丝杠滚珠接触点A和螺母滚珠接触点B建立坐标系AX_AY_A $ {\textit{Z}}_{{A}}$ 和BX_BY_B $ {\textit{Z}}_{{B}}$ ，原点A和B位于刚接触上时（即没有正压力时）的接触点， $ {\textit{Z}}_A$ 轴和 $ {\textit{Z}}_B$ 轴分别垂直于与接触点处的共切平面，X_A轴和X_B轴平行于滚珠中心轨迹螺旋线的切向方向t，Y_A轴和Y_B轴由右手定则确定。

图1(Fig. 1)

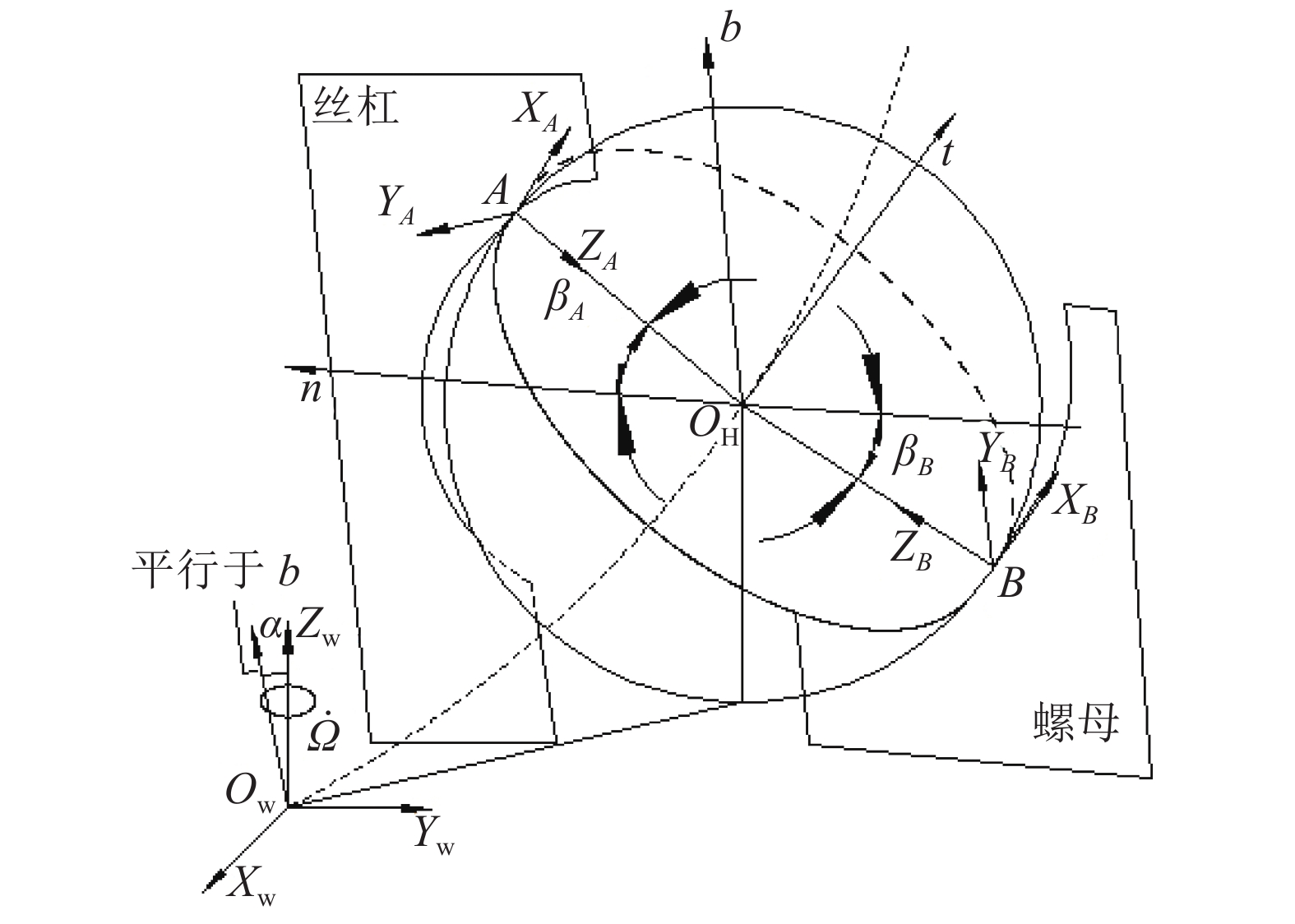图1 滚珠丝杠副系统的坐标系 Fig. 1 Coordinate system of ball screw mechanism

在图1中，坐标系O_WX_WY_W $ {\textit{Z}}_{\rm{W}}$ 为惯性参考坐标系，使 $ {\textit{Z}}_{\rm{W}}$ 轴与丝杠的中心轴线重合，但不随丝杠旋转； $ OXY{\textit{Z}}$ 为与丝杠固联并随丝杠绕轴线旋转的坐标系，且 $ {\textit{Z}}$ 轴与丝杠轴线重合，使X轴与滚珠球心轨迹形成的螺旋线相交；O_Htnb为滚珠球心轨迹形成的螺旋线上任意一点的Frenet–Serret坐标系，各个坐标轴的方向随着原点在曲线上的位置不同而发生变化。原点O_H位于螺旋线上，且与螺旋曲线（即丝杠）的相对位置由底角θ确定；t为螺旋线的切线方向且沿着螺旋线的上升方向；n为螺旋线的主法线方向；b为螺旋线的副法线方向。

为了准确地描述滚道接触点处的几何形状、接触变形和接触应力，需要建立滚道接触点处的坐标系，如图2所示。

图2(Fig. 2)

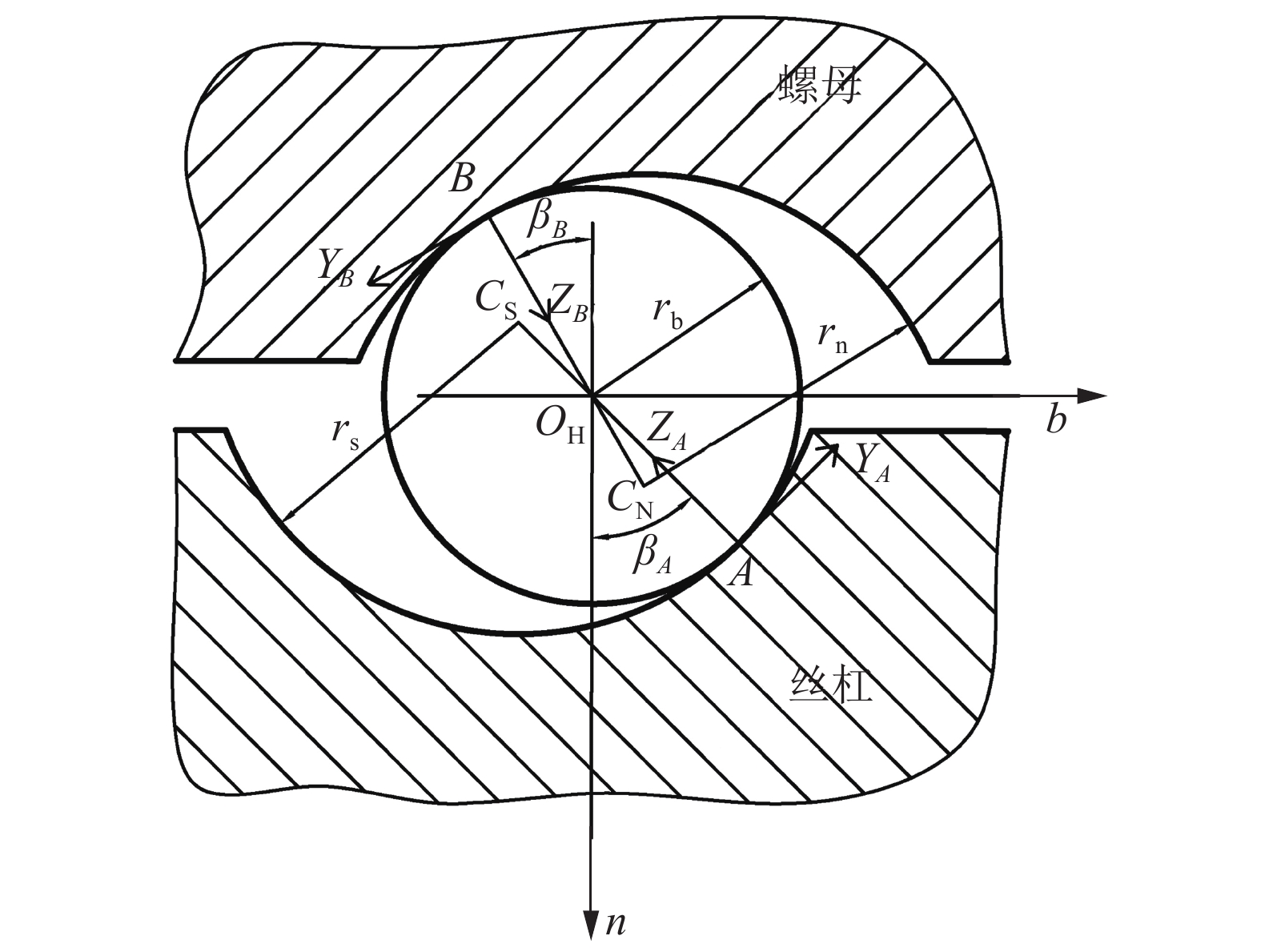图2 滚珠丝杠副接触坐标系 Fig. 2 Contact coordinate system of ball screw mechanism

由于滚珠的对称性，在两个接触点坐标系下滚珠表面形貌的参数方程均相同，可表示为^[16-17]：

式中，A和B分别为丝杠与滚珠、螺母与滚珠的接触点。滚道表面几何形貌在接触点A和B处所建立的坐标系下的参数方程可通过坐标转换的方法获得。Frenet–Serret坐标系O_Htnb中，接触点A附近丝杠滚道截面圆弧的参数表达式为：

式中，r_S为丝杠滚道截面圆弧半径，r_b为滚珠半径，β_A为滚珠与丝杠滚道之间的接触角，β_AS为所分析丝杠滚道区域截面圆弧段对应的圆心角，β_A0用于定义丝杠滚道圆心角的范围。

同理，可得接触点B附近螺母滚道截面圆弧的参数表达式。

根据式（1）、（2）及坐标转换理论，可以得到丝杠滚道圆弧参数方程在接触坐标系AX_AY_A $ {\textit{Z}}_A$ 下的表达式：

同理，可得螺母滚道圆弧参数方程在接触坐标系BX_BY_B $ {\textit{Z}}_B$ 下的表达形式：

式中， ${{T}}_{\rm{S}}^{\rm{H}} $ 表示从丝杠固联坐标系 $ OXY{\textit{Z}}$ 到Frenet–Serret坐标系O_Htnb的坐标转换矩阵， ${{T}}_{\rm{H}}^A$ 和 ${{T}}_{\rm{H}}^B$ 分别表示由坐标系O_Htnb到坐标系AX_AY_A $ {\textit{Z}}_{{A}}$ 和BX_BY_B $ {\textit{Z}}_{{B}}$ 的坐标转换矩阵，θ_C为滚珠和滚道接触点A或B处对应的旋线圆心角。

由滚道圆弧参数方程（3）和（4）可以得到滚道曲面形貌即丝杠滚道和螺母滚道接触点附近区域在接触点坐标系中的分布情况。但是，3维表面在接触点坐标系的平面AX_AY_A和BX_BY_B上的投影并非规则的矩形区域，因此，需要通过2维插值算法，重新进行网格划分，以便于后续的接触力学分析。滚道曲面插值结果如图3所示。

图3(Fig. 3)

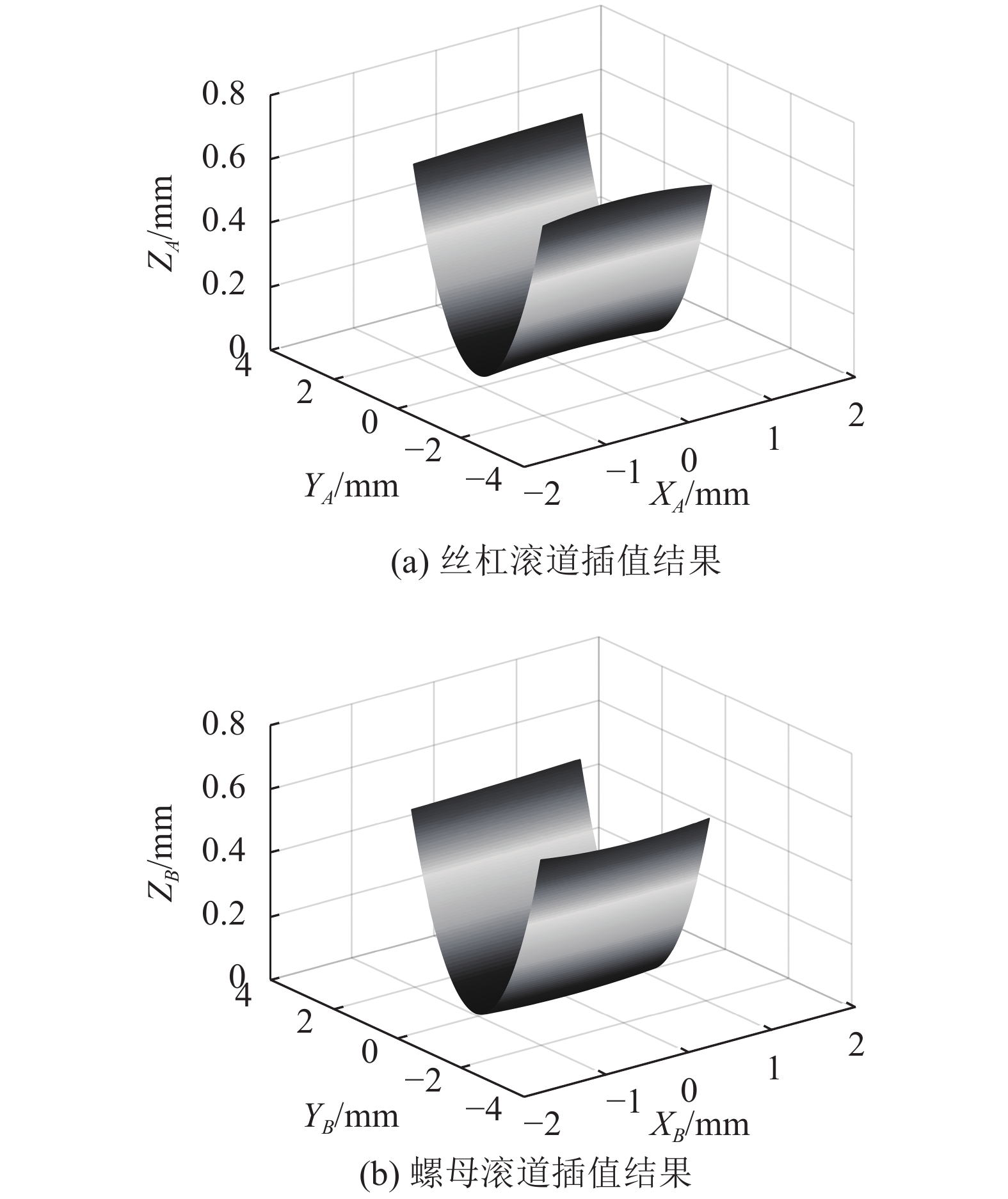图3 滚道曲面插值结果 Fig. 3 Interpolation results of raceway surface

当一个球和一个弹性半无限体的接触，在求解接触应力分布的数值解时，首先要对接触区域和控制方程进行离散。为计算方便，不考虑摩擦力对接触应力计算的影响，给出的方程都是离散化形式，其中M和N分别为x与y方向的网格点数。两表面的接触间隙和接触压力满足如下方程^[14]：

式中，c_i，j为接触表面间隙矩阵c的元素，d₀为刚体接近距离，c_gi，j为接触体几何形状矩阵c_g的元素，c_ri，j为接触体表面粗糙度矩阵c_r的元素，V_i，j为表面弹性变形矩阵V的元素。

表面弹性变形的离散形式的计算方程为：

式中，p_i，j为接触压力矩阵P的元素，k_{i–k，j–l}为变形影响系数矩阵K的元素。

同时接触间隙和接触压力要满足的约束条件为：

在接触区内，c_i，j=0，p_i，j≥0；在接触区外，c_i，j>0，p_i，j=0。显然，c_i，j和p_i，j不能同时为0，即：

对于两弹性体接触表面产生的弹性变形的计算，传统的计算方法是在单元网格上用多项式近似压力分布得到影响系数后采用直接矩阵相乘的方法来计算弹性变形。但为了达到较高的精度，需要对网格进行细分，这样会显著增加计算量，效率较低。Brandt等^[18]提出了多重网格积分法，在求解带有粗糙表面的接触问题时可以得到较为精确的结果，且计算效率较高。

由于接触表面变形的计算相当于求影响系数矩阵与法向应力之间的卷积，因此，在数值求解过程中，采用快速傅里叶变换（FFT）方法可以方便快速地计算弹性变形。通过该方法求解接触变形量分布的计算步骤可参考文献[14]。计算结果表明采用快速傅里叶变换计算弹性变形能够达到所需精度，而且计算效率得到明显提高。

接触问题的核心就在于求解压力分布和接触体表面几何形貌之间的关系，式（5）～（8）所描述的接触问题实际上构成一个线性补余问题，可用矩阵形式表示^[14]：

式中，c_i，j为常数矩阵c的元素； ${\tilde c _{i,j}} = {d_0} + {{\rm{c}}_{gi,j}} + {{\rm{c}}_{ri,j}}$ 。

根据变分原理，方程式（9）和（10）所描述的接触问题可以转化为二次函数的条件极值问题。该原理可表示为寻找目标函数：

在约束条件c_i，j≥0，p_i，j≥0，c_i，jp_i，j=0下的极小值。

通过变分原理将接触问题转化为式（11）所描述的极值问题后，可以采用共扼梯度法进行循环迭代来实现快速收敛。作者所使用的共轭梯度法收敛性的详细证明和迭代求解过程可参考文献[14, 19]。

在研究滚珠丝杠副中滚珠与滚道之间的接触状态时，国内外许多学者均采用赫兹接触理论来进行近似分析。但是由于滚道曲面形状的复杂性和非对称性，因此直接采用赫兹接触模型计算是不精确的。为了验证基于最小余能原理接触应力分布的数值解即非赫兹解的正确性，将该原理与赫兹接触理论分别用于求解光滑的球与平面之间的弹性接触应力分布，并将两种方法的计算结果进行对比分析^[17]。

赫兹接触理论^[20]提出了针对两个不同球体之间弹性接触问题的经典解。根据该理论，使其中一个球体的半径趋于无穷大，即可得到光滑圆球与光滑平面接触时以半径为a的圆形接触区域内的赫兹接触压力分布的解析解即赫兹解。

式中， $ F_{\textit{z}}$ 为两个接触体之间的法向负载。当r=0时，得到接触区域内的最大接触应力P_max，位于接触区域中心。

法向负载 $ F_{\textit{z}}$ 与法向趋近量 $ \delta _{\textit{z}}$ 之间的关系为：

式中，E^*为等效弹性模量，R^*为等效接触半径，表达式分别为：

式中，E₁、E₂和ν₁、ν₂分别为两接触体的弹性模量和泊松比，R₁为球体的半径，R₂ $ \to + \infty $ 表示平面。

接触区域半径与法向趋近量之间的关系为：

根据式（12）～（15）即可求出光滑圆球与光滑平面接触应力分布的情况，两种方法的计算结果如图4所示，其中实线表示接触应力分布的赫兹解。从图4中，可以看出非赫兹解与赫兹解的重合度很好，因此验证了前述非赫兹解的正确性。

图4(Fig. 4)

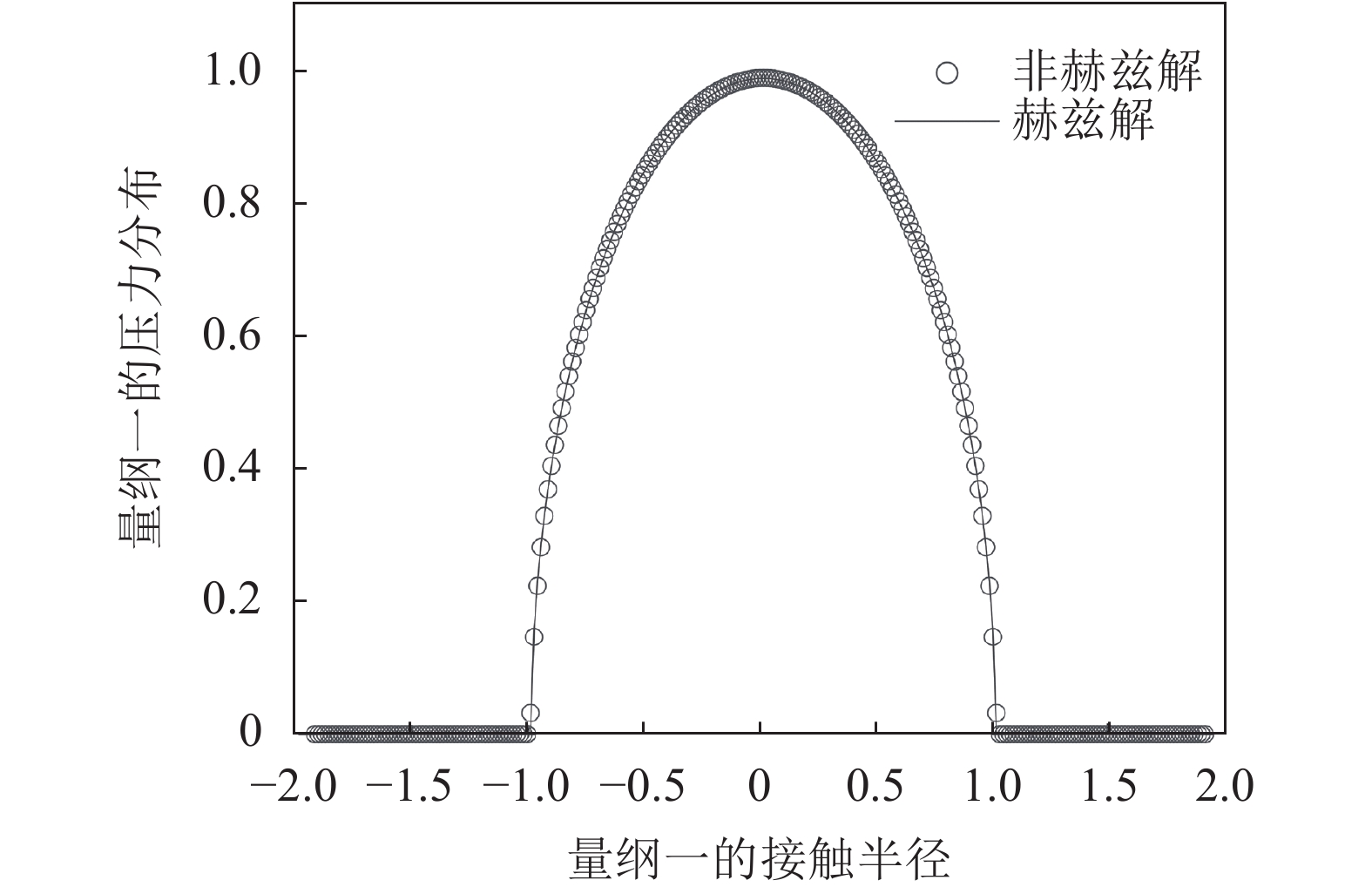图4 球与平面弹性接触压力分布的非赫兹解 Fig. 4 Comparison of the non-Hertzian and Hertzian solutions for the pressure distribution of the elastic contact between a ball and a plane

为了更加准确、全面描述滚珠丝杠副的接触应力分布情况，分别基于最小余能原理和采用赫兹接触理论对滚珠丝杠副中滚珠与滚道的接触问题进行详细计算，并对比分析两种方法的计算结果。

在求解过程中，法向正压力取170 N并综合考虑了滚道的实际3维曲面形貌，图5和6分别给出了螺旋升角为32.48°时滚珠丝杠副接触点A和接触点B处接触区域上应力分布的赫兹解、非赫兹解。由图5和6可知，两种求解方法所得接触应力分布存在一定差异，这是由于其接触区域的非对称性变化造成的。同时，可以看到丝杠滚珠接触点A处接触应力比螺母滚珠接触点B处接触应力稍大一些，这是因为两接触点处的滚道3维表面形貌不同。

图5(Fig. 5)

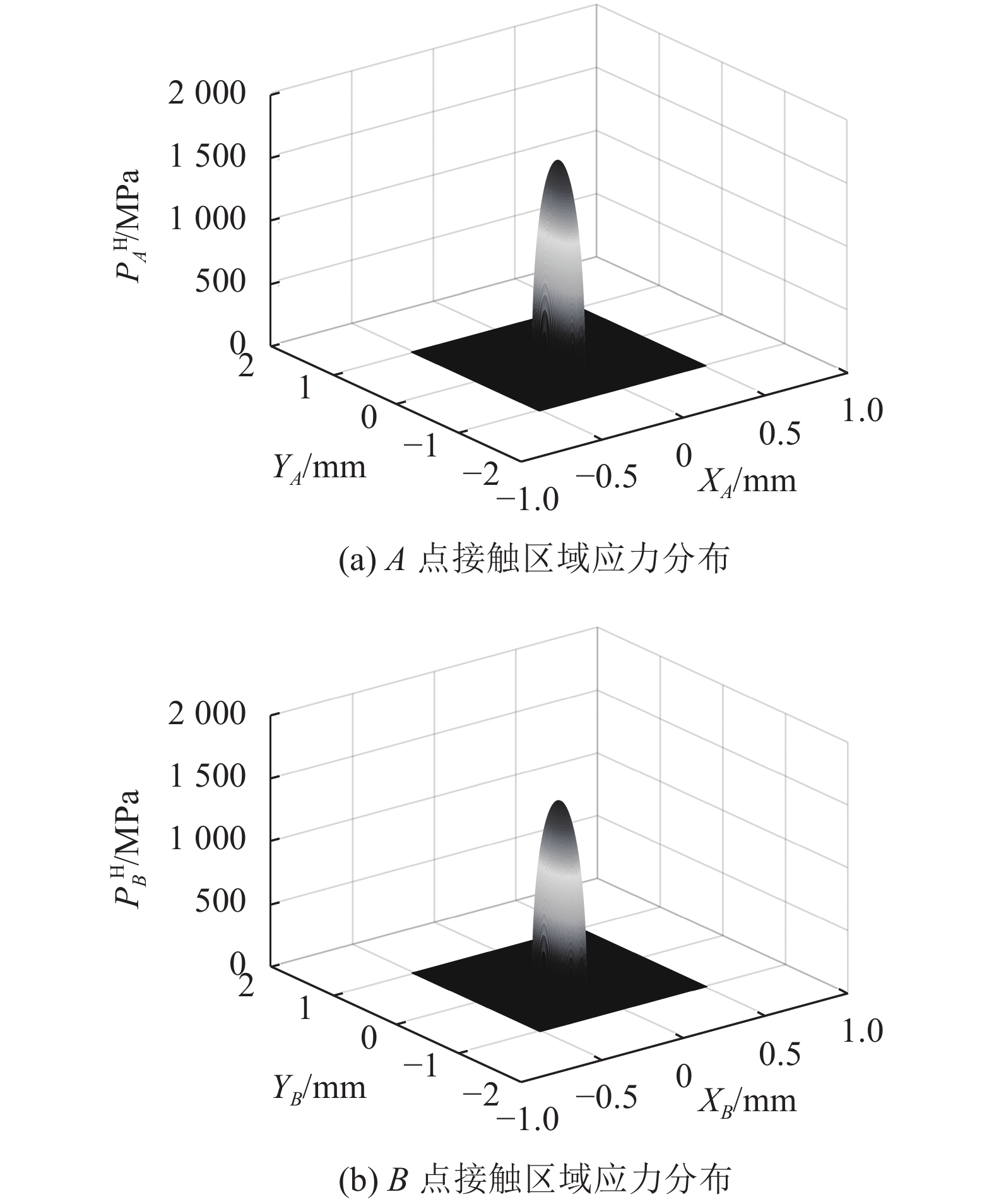图5 螺旋升角为32.48°时接触区域应力分布赫兹解 Fig. 5 Hertzian solution of stress distribution in contact area with helix rise angle of 32.48°

图6(Fig. 6)

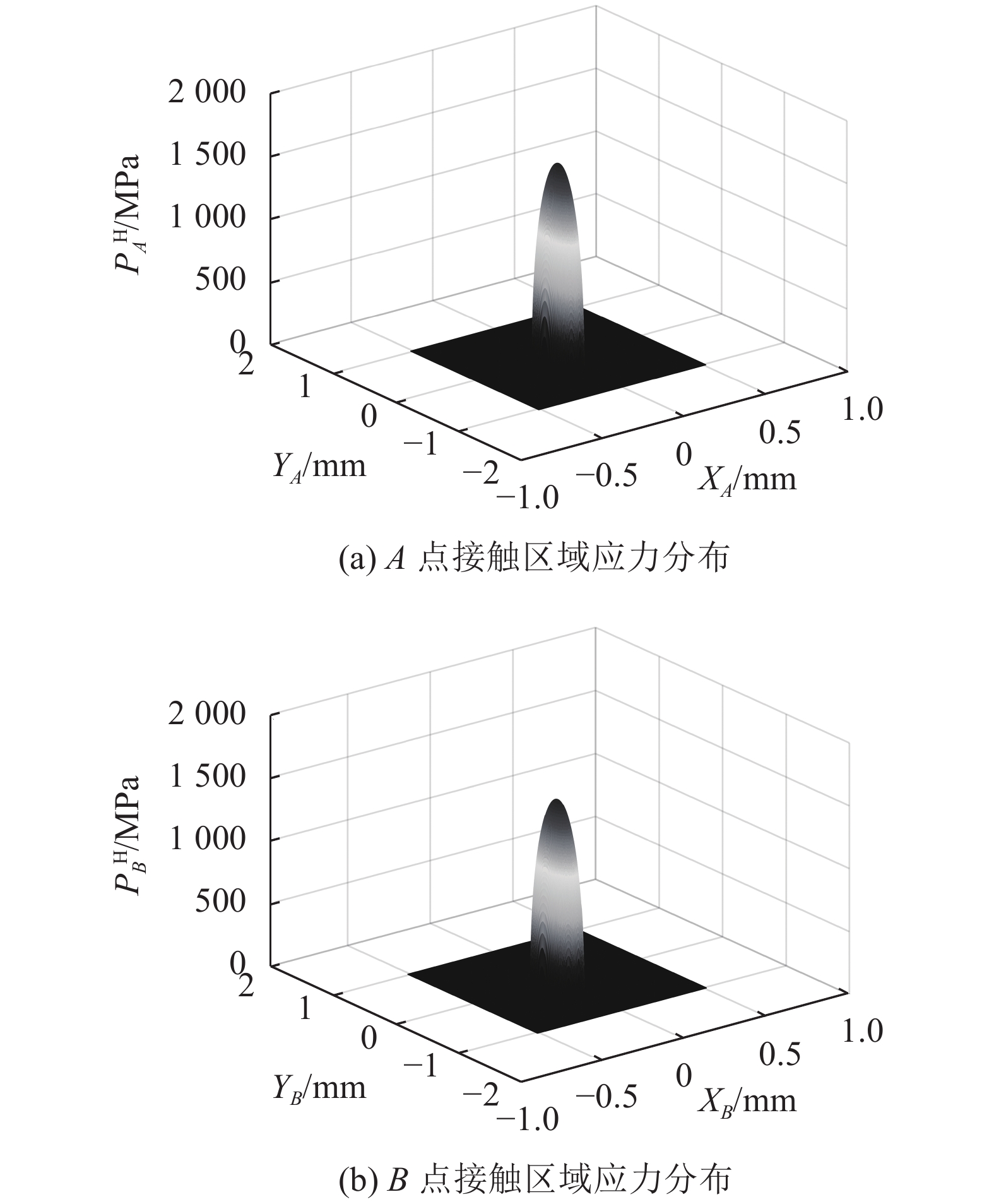图6 螺旋升角为32.48°时接触区域应力分布非赫兹解 Fig. 6 Non-Hertzian solution of stress distribution in contact area with helix rise angle of 32.48°

为了对比两种方法计算结果的不同，图7给出了螺旋升角为32.48°时滚珠丝杠副接触点A和接触点B处应力的非赫兹解与赫兹解之差的等高线图。由图7可知，两种解法所得结果存在较大的不同，尤其是接触区域的边缘处应力差值最大，距离接触中心越近差值越小。因此，采用赫兹接触理论求解滚珠丝杠副的接触应力将产生较大的误差，而采用非赫兹解来分析滚道的接触应力分布情况计算精度更高，且方法简便。

图7(Fig. 7)

图7 螺旋升角为32.48°时接触点处应力的非赫兹解与赫兹解之差的等高线图 Fig. 7 Contour map of the difference between the non-Hertzian solution and the Hertzian solution of the stress at the contact point with helix rise angle of 32.48°

图8和9为两种方法计算得到滚珠与滚道接触点处接触应力分布的等高线图。非赫兹解所得接触椭圆相比赫兹解所得接触椭圆存在一定的偏斜，而且通过计算可求得接触区域的面积和长短轴，两种解法存在一定差异。其中，接触区域应力分布情况可以反映丝杠和螺母滚道因法向压力引起的磨损量在滚道上形成的磨损带的深度和宽度。此外，两种计算方法所得接触点B处接触面积大于接触点A处接触面积，这与第3.2节中接触点A、B处接触应力存在不同相符合。

图8(Fig. 8)

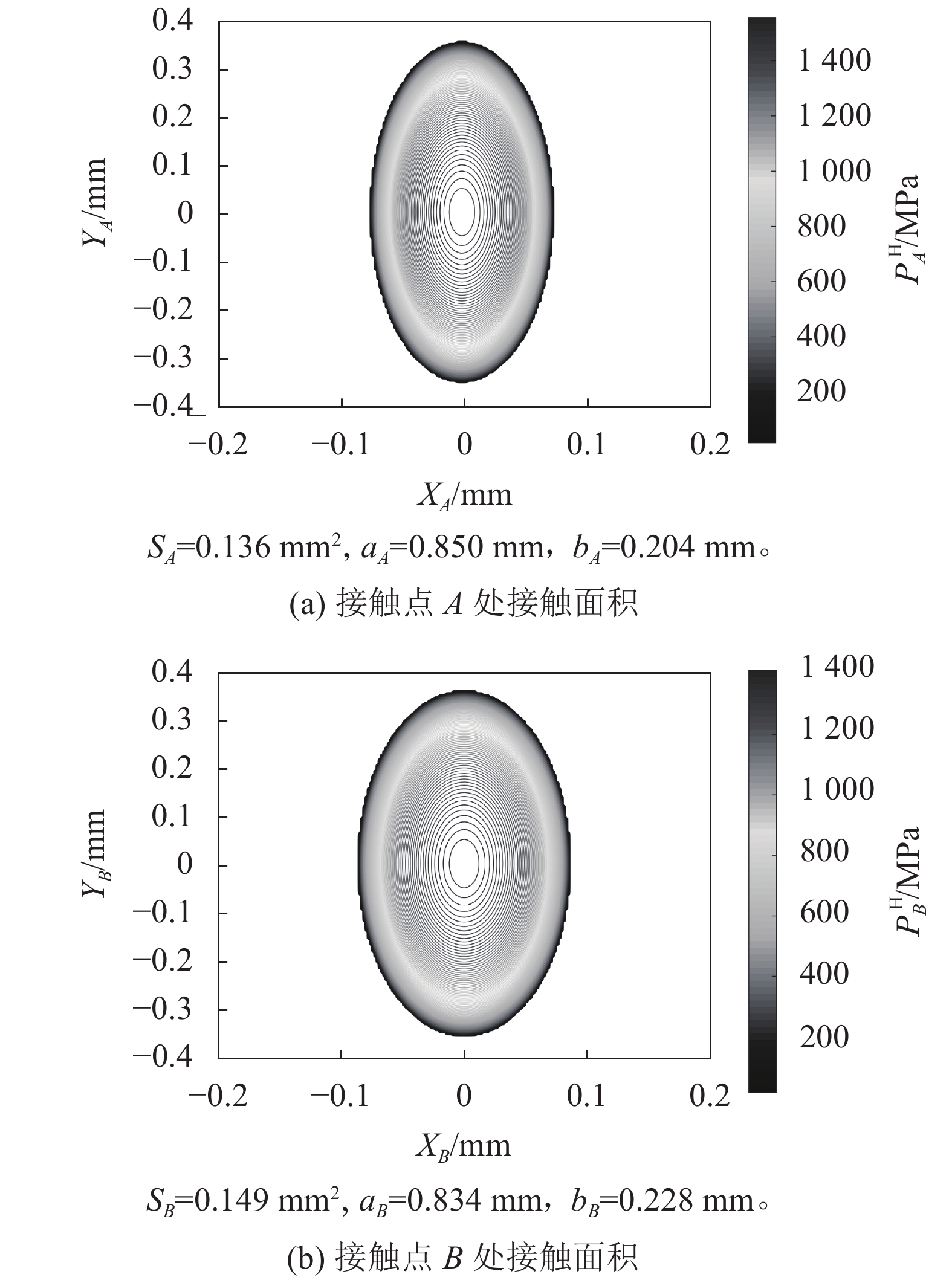图8 赫兹解的接触区域 Fig. 8 Contact area calculated by Hertzian method

图9(Fig. 9)

图9 非赫兹解的接触区域 Fig. 9 Contact area calculated by non-Hertzian method

为了进一步分析滚珠丝杠副螺旋升角的变化对赫兹接触理论所得接触应力计算误差的影响，图10分别给出了螺旋升角为4.55°、10.81°和17.66°时丝杠滚珠接触点A处应力的非赫兹解与赫兹解之差的等高线图，其中，E_max是滚珠丝杠副接触点A处赫兹接触应力相对于非赫兹接触应力的最大计算误差，由图10可见该误差随着螺旋升角的增大而增大。

图10(Fig. 10)

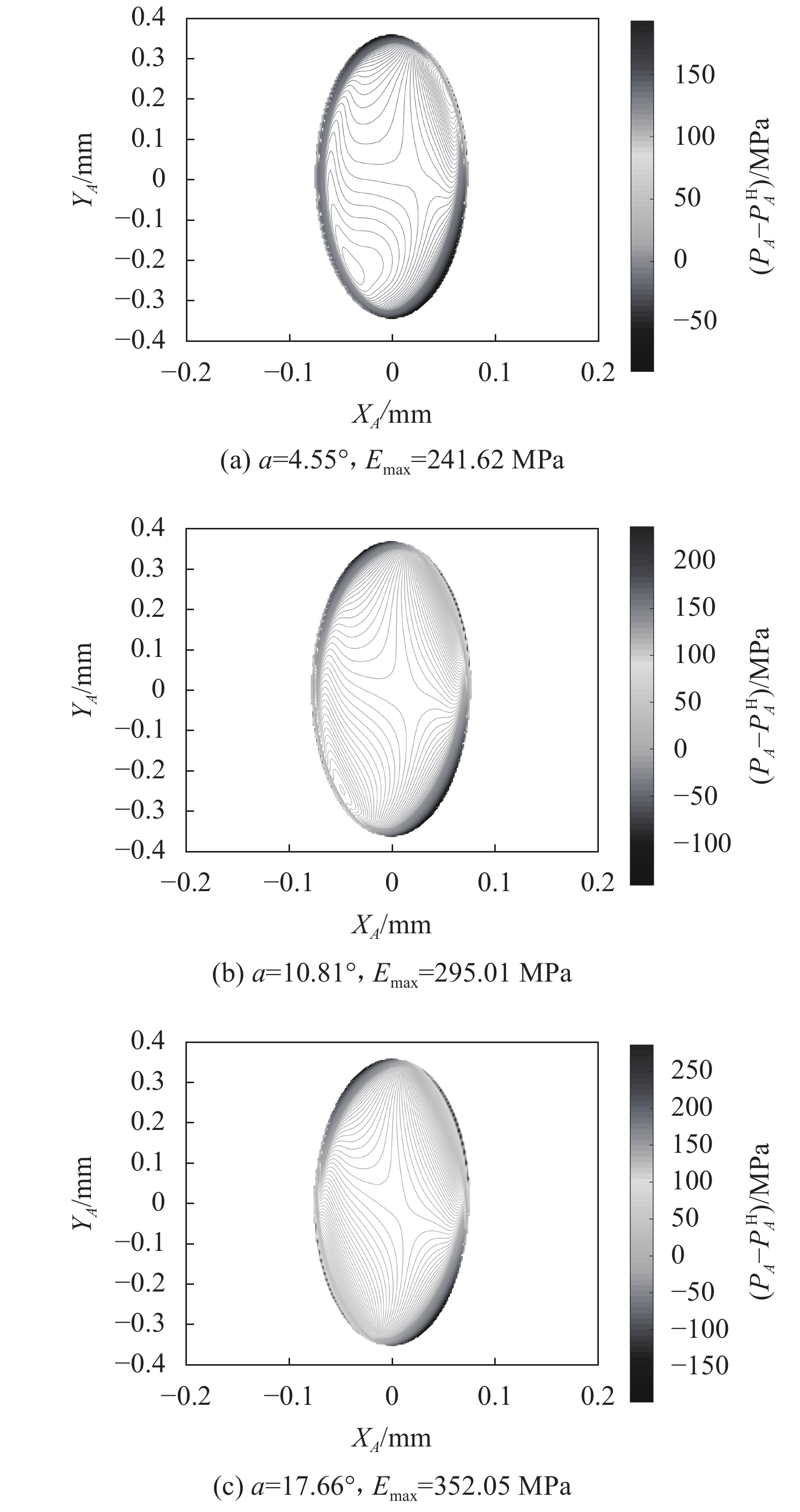图10 丝杠–滚珠接触点A处应力的非赫兹解与赫兹解之差 Fig. 10 Difference between non-Hertzian solution and Hertzian solution of stress at contact point A

图11给出了赫兹解相对于非赫兹解的接触应力误差随螺旋升角的增大而逐渐增大的趋势图。由图11可知，丝杠与滚珠接触点A处的误差始终大于螺母与滚珠接触点B处的误差。随着机床的高速化、精密化的发展，螺旋升角逐渐变大，导致接触区域的非对称性更大。因此，当采用赫兹接触理论计算滚珠丝杠副的接触应力时，将会带来更大的误差。

图11(Fig. 11)

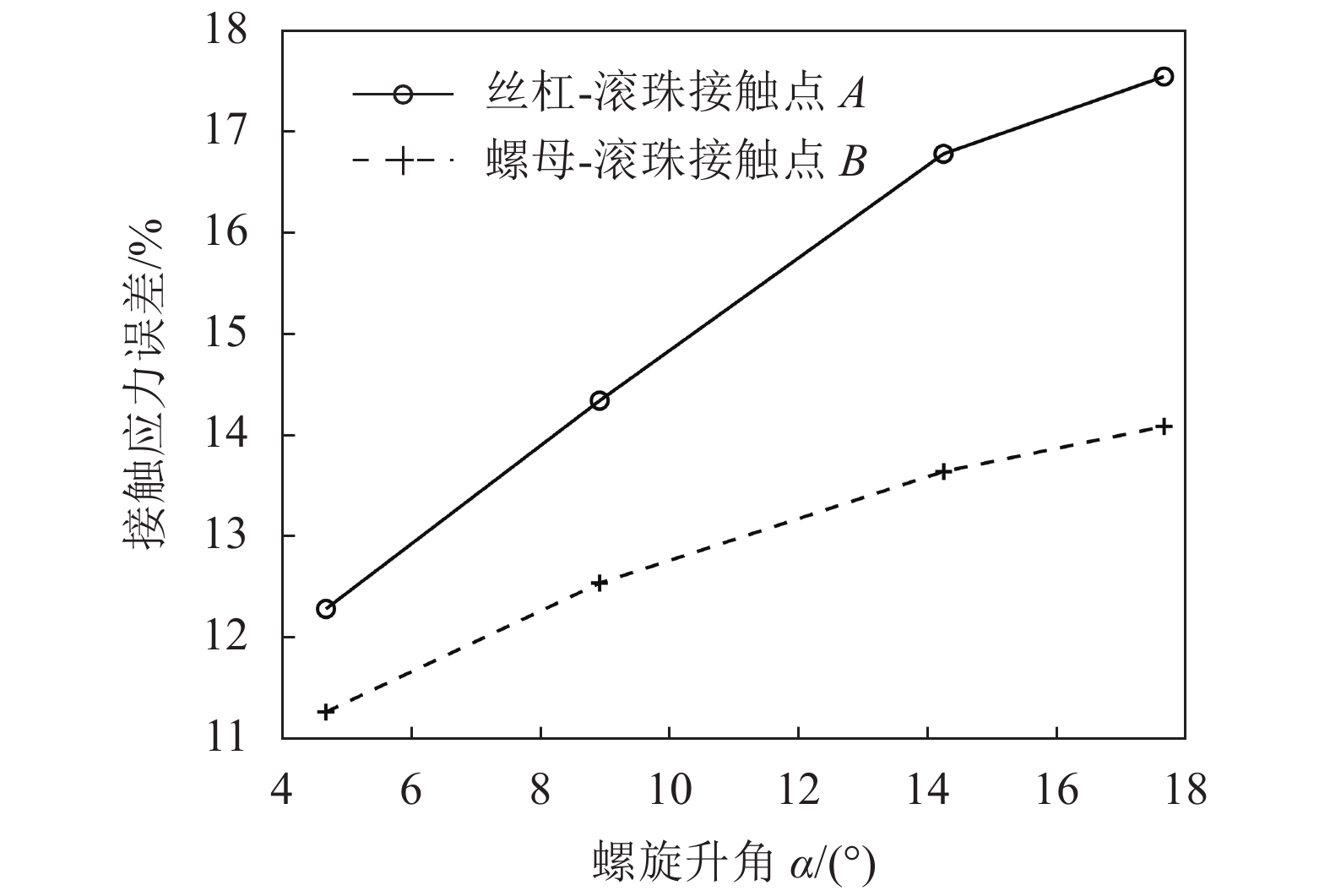图11 赫兹解相对于非赫兹解的接触应力误差 Fig. 11 Contact stress error of Hertzian solution relative to non-Hertzian solution

图12中给出了滚珠丝杠副接触点处非赫兹解和赫兹解的接触应力峰值随螺旋升角增大的变化情况。由图12可知，滚珠丝杠副螺旋升角的变化对接触点处赫兹解接触应力峰值影响不大。但是，随着螺旋升角的增加，丝杠滚道与滚珠接触点A处非赫兹解接触应力峰值逐渐变小；螺母滚道与滚珠接触点B处非赫兹解接触应力峰值逐渐增大，且接触点A处应力峰值始终大于接触点B处峰值。

图12(Fig. 12)

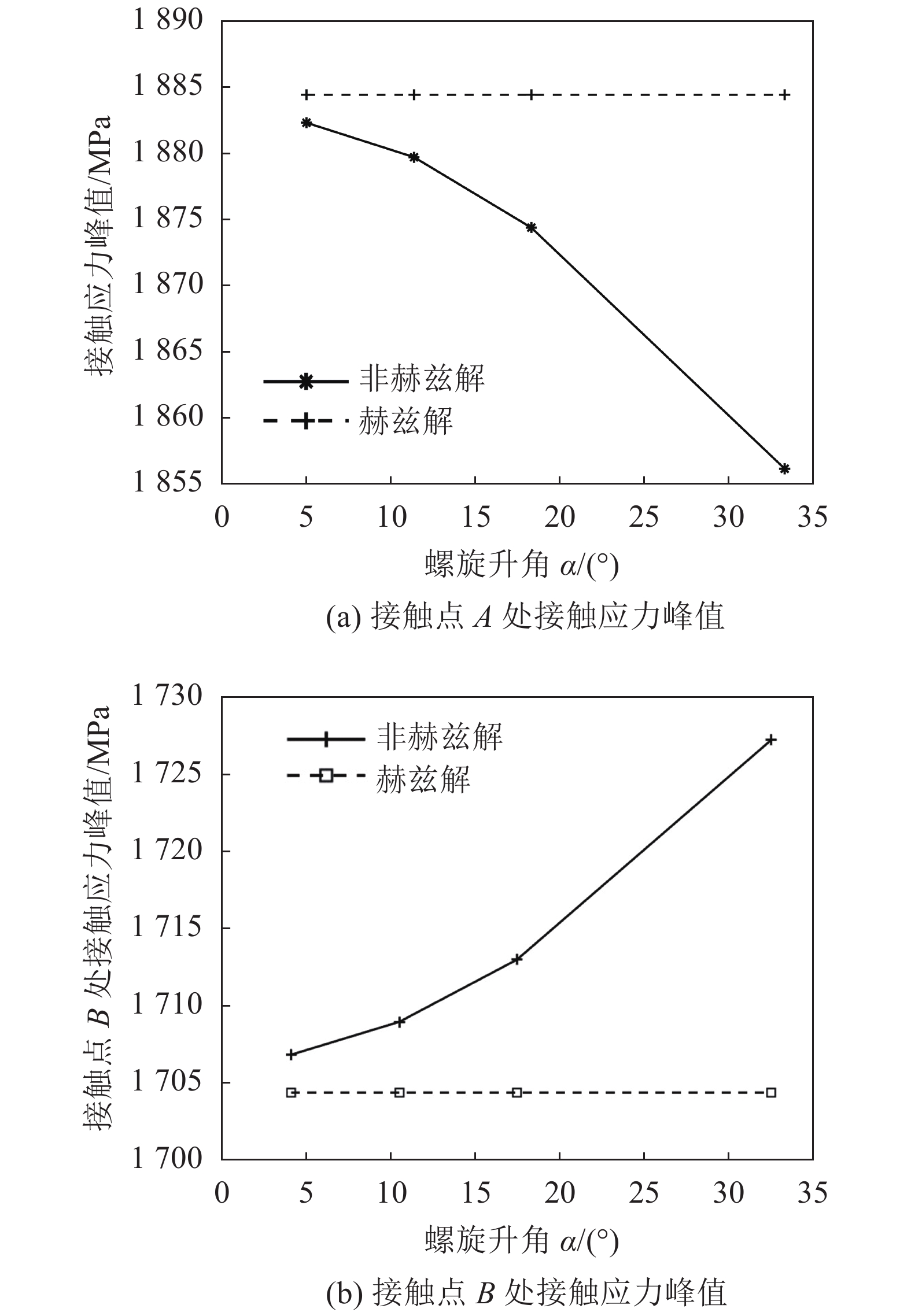图12 接触点处非赫兹解和赫兹解的接触应力峰值 Fig. 12 Peak value of contact stress of non-Hertzian solution and Hertzian solution at the contact point

为了研究滚珠丝杠副滚道曲面的应力分布，并考虑接触区域的非对称性，克服采用赫兹接触理论计算所带来的误差，基于最小余能原理对滚珠与滚道进行接触应力分析，可以得到以下结论：

1）赫兹接触解与最小余能非赫兹接触精确解相比，当螺旋升角增加时，丝杠滚道和螺母滚道与滚珠接触点处接触应力误差逐渐增大。而且，随着滚珠丝杠副螺旋升角的增大，丝杠滚道与滚珠接触点处的误差始终大于螺母滚道与滚珠接触点处的误差。

2）赫兹解和非赫兹解两种方法计算所得滚珠与滚道接触区域的面积和长短轴有所不同。准确计算滚珠和滚道接触区域应力分布可以更加全面和准确的计算滚道磨损带的宽度和深度。

3）随着数控机床高速高精化发展，具有大螺旋升角的高速滚珠丝杠副应用越来越广泛。由于高速滚珠丝杠副接触区域非对称性大，有必要采用最小余能原理进行接触应力分析，以便更准确的分析高速滚珠丝杠副的磨损机理和预测其精度保持性。