视频前背景分离一直是计算机视觉等领域研究的热点，但是由于自然界存在的噪声、模糊、遮挡和光照变化等的干扰，使其成为最具有挑战性的问题之一。在此背景下，如何根据视频先验信息，构造鲁棒性强、复杂度低的视频前背景分离方案是其关键难题。鲁棒主成分分析（robust principal component analysis，RPCA）^[1]作为多媒体信息处理领域的前沿技术，被广泛应用于视频前背景分离^[2-5]中，同时，也是视频去噪^[6]和人脸阴影移除^[7]等领域的关键技术。传统RPCA是一种将观测矩阵分解为低秩矩阵和稀疏矩阵的方法，所以又被称为稀疏低秩分解（sparse and low-rank decomposition，SLRD）。但是，由于该问题的非凸、非连续性等特点使传统RPCA问题难以直接求解，且其是NP–难问题。为了求解该问题，主成分追踪（principal component pursuit，PCP）算法^[8]被提出，该算法分别采用核范数和 $ {\rm L_1} $ 范数替代传统RPCA模型中的秩函数和 $ {\rm L_0} $ 范数。PCP算法能够较好地解决多媒体信息处理领域中的诸多问题^[8]，尤其是推动了视频前背景分离^[9]、矩阵填充^[10]等技术领域的发展，并逐渐成为引领RPCA方法发展的基础框架。但PCP算法也存在诸如时间复杂度高，平等对待所有奇异值，不能较好逼近秩函数和 $ {\rm L_0} $ 范数，抗噪声能力弱以及不考虑结构化、运动化信息等缺陷。针对PCP算法存在的以上问题，改进的RPCA算法被提出并被应用于视频前背景分离。

改进的算法主要分为凸替代RPCA方法、非凸替代RPCA方法、加入辅助信息的RPCA方法以及截断核范数方法。例如，去分解（go decomposition，GoDec）算法^[11]是一种经典的凸替代RPCA方法，它将受环境污染的观测矩阵分解为低秩、稀疏和噪声矩阵，增强了PCP算法的鲁棒性，同时，采用双边随机预测（bilateral random projections，BRP）方法^[11]优化算法时间复杂度，提高算法收敛速度，但是，凸替代方法对秩函数和稀疏度函数的逼近程度不高，效果欠佳。在此基础上，一系列非凸替代RPCA方法被陆续提出，例如，非凸非光滑加权核范数（nonconvex nonsmooth weighted nuclear norm，NNWNN）算法^[12]、非凸低秩稀疏分解（nonconvex low-rank and sparse decomposition，NonLRSD）算法^[13]、非凸秩逼近（nonconvex rank approximation，NRA）算法^[14]、广义双步长（general dual step-size，GDSS）算法^[15]、线性分类非凸（linear spectral clustering and non-convex，LSCNC）算法^[16]、带有分割稀疏的非凸RPCA（non-convex and segmentation constraint，NCSC）算法^[17]、核化的非凸全变差RPCA（nonconvex total variation regularized RPCA with kernelization，KRPCA–NTV）算法^[18]等，这些非凸替代RPCA方法采用较为先进的非凸替代函数替换传统RPCA中的秩函数和稀疏度函数。但是，由于该类算法的替代函数仍然非最优，同时，容易忽略视频中的结构化信息，使得视频前背景分离的效果差强人意。考虑到视频中存在大量的时空信息，于是许多基于辅助信息的RPCA方法被提出并应用于视频前背景分离中，例如：基于低秩和结构化的稀疏分解（low-rank and structured sparse decomposition，LSD）算法^[19]采用结构化稀疏诱导范数描述矩阵的稀疏成分，并将空间信息引入到RPCA算法模型中；基于运动信息辅助的矩阵恢复（motion-assisted matrix restoration，MAMR）算法^[20]将运动信息引入到传统RPCA模型中，辅助信息的加入促进了矩阵分解的准确性，尤其对受光照变化、水纹波动等影响的观测矩阵分解效果明显。但是，该类算法较难描述视频中的辅助信息，视频前背景分离效果不稳定，同时，由于大量辅助信息计算的引入导致算法时间复杂度较高，视频前背景分离的时间较长。

截断核范数（truncated nuclear norm，TNN）算法^[21-23]是为了解决PCP算法中核范数平等对待所有奇异值的问题而提出的一种更逼近秩函数的方法。与传统RPCA不同的是，TNN算法是对 $ \min (m,n) - r $ 个奇异值进行最优化计算，并最终将传统RPCA模型转换为一个凸优化问题进行求解。通过大量的理论论证和实验验证表明TNN能够取得较好的视频前背景分离效果。在TNN算法的基础上，诸多改进的TNN算法陆续被提出并广泛应用于视频前背景分离中，例如，Hu等^[21]提出了一种基于截断核范数和稀疏正则化（truncated nuclear norm and a sparse regularizer，TNNSR）的低秩稀疏分解算法，该算法在TNN的基础上增加了稀疏先验项，提高了TNN算法的鲁棒性。虽然大量实验表明TNN及其改进算法在视频前背景分离中具有较好的效果，但是由于TNN模型中的核范数仍然是凸替代函数，逼近程度弱，算法效果欠优，仍然亟待改进。

本文提出了一种改进的截断核范数（improved truncated nuclear norm，ITNN）算法，为了增强TNN算法对传统RPCA算法的逼近度，该算法采用非凸 $\gamma $ 范数替代TNN算法中的核范数，并从理论上分析了非凸 $\gamma $ 范数比核范数逼近度更高的原因。同时，本文采用广义交替方向乘子法（generalized alternating direction method of multipliers，GADMM）^[24-25]求解ITNN算法模型。最后，将ITNN算法及其对比算法应用到视频前背景分离实验中，验证ITNN算法的有效和优越性。

1 改进的截断核范数 1.1 改进的截断核范数的模型

鉴于矩阵 $ {\boldsymbol{M}} $ 的秩与其较小的 $ \min (m,n) - r $ 个非零奇异值相关，TNN算法将传统的RPCA模型转换为如式（1）所示的模型：

$ \begin{array}{l} \mathop {{\text{min}}}\limits_{{\boldsymbol{L}}{\text{,}}{\boldsymbol{S}}} \displaystyle\sum\limits_{i = r{\text{ + 1}}}^{\min (m,n)} {{\sigma _i}({\boldsymbol{L}})} {\text{ + }}\lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\text{s}}{\text{.t}}{\text{. }}\;\;\;\;{\boldsymbol{ M}}{\text{ = }}{\boldsymbol{L}}{\text{ + }}{\boldsymbol{S}} \end{array} $

(1)

式中， $ {\boldsymbol{M}} \in {{\mathbb{R}}^{{\boldsymbol{m}} \times {\boldsymbol{n}}}} $ 为已知的观测矩阵， $ {\boldsymbol{L}} \in {{\mathbb{R}}^{{\boldsymbol{m}} \times {\boldsymbol{n}}}} $ 为低秩矩阵， $ {\boldsymbol{S}} \in {{\mathbb{R}}^{{\boldsymbol{m}} \times {\boldsymbol{n}}}} $ 为稀疏矩阵， $ {\sigma _i}({\boldsymbol{L}}) $ 为矩阵 $ {\boldsymbol{L}} $ 的奇异值， $ r $ 为截断的奇异值个数。

但是，由于 $\displaystyle \sum\limits_{i = r{\text{ + 1}}}^{\min (m,n)} {{\sigma _i}({\boldsymbol{L}})} $ 为非凸函数，难以直接求解，于是将式（1）转换为如下模型：

$ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{l} \mathop {{\text{min}}}\limits_{{\boldsymbol{L}}{\text{,}}{\boldsymbol{S}}} {\left\| {\boldsymbol{L}} \right\|_{{*}}} - \displaystyle\sum\limits_{i = 0}^r {{\sigma _i}({\boldsymbol{L}})} {\text{ + }}\lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\text{s}}{\text{.t}}{\text{. }}\;\;\;\;{\boldsymbol{ M}}{\text{ = }}{\boldsymbol{L}}{\text{ + }}{\boldsymbol{S}} \end{array}} $

(2)

由文献[21]可知，式（2）可以转换为如下问题：

$ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{l} \mathop {{\text{min}}}\limits_{{\boldsymbol{L}}{\text{,}}{\boldsymbol{S}}} {\left\| {\boldsymbol{L}} \right\|_{{*}}} - \mathop {\max }\limits_{_{{\boldsymbol{A}}{{\boldsymbol{A}}^{\text{T}}} = {\boldsymbol{I}}, {\boldsymbol{B}}{{\boldsymbol{B}}^{\text{T}}} = {\boldsymbol{I}}}} {\text{tr}}\left( {{{\boldsymbol{A}}^{\text{T}}}{\boldsymbol{LB}}} \right){\text{ + }}\lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\text{s}}{\text{.t}}{\text{. }}\;\;\;\;{\boldsymbol{ M}}{\text{ = }}{\boldsymbol{L}}{\text{ + }}{\boldsymbol{S}} \end{array} }$

(3)

式中： $ {\boldsymbol{A}}{\text{ = }}({u_1},{u_2}, \cdots ,{u_r}) \in {{\mathbb{R}}^{m \times r}} $ 为低秩矩阵 $ {\boldsymbol{L}} $ 的前 $ r $ 个左奇异向量； $ {\boldsymbol{B}}{\text{ = }}({v_1},{v_2}, \cdots ,{v_r}) \in {{\mathbb{R}}^{n \times r}} $ 为低秩矩阵 $ {\boldsymbol{L}} $ 的前 $ r $ 个右奇异向量；核范数 $ {\left\| {\boldsymbol{L}} \right\|_{{*}}} $ 为秩函数的凸有偏估计，其对秩函数的逼近程度低。研究表明非凸替代函数能更好地逼近传统RPCA模型中的秩函数^[12-18]。本文采用非凸 $\gamma $ 范数^[14]替代TNN算法中的核范数， $\gamma $ 范数的表达式如下：

$ {\left\| {\boldsymbol{L}} \right\|_\gamma } = \sum\limits_i {\frac{{(1 + \gamma ){\sigma _i}({\boldsymbol{L}})}}{{\gamma + {\sigma _i}({\boldsymbol{L}})}}} $

(4)

式中， $ i{\text{ = }}1,2, \cdots ,\min (m,n) $ 。又因为：

$ \begin{array}{l} \mathop {\lim }\limits_{\gamma \to \infty } {\left\| {\boldsymbol{L}} \right\|_\gamma } = \mathop {\lim }\limits_{\gamma \to \infty } \displaystyle\sum\limits_i {\frac{{\left(\dfrac{1}{\gamma } + 1\right){\sigma _i}({\boldsymbol{L}})}}{{1 + \dfrac{{{\sigma _i}({\boldsymbol{L}})}}{\gamma }}}} {\text{ = }}\displaystyle\sum\limits_i {{\sigma _i}({\boldsymbol{L}}){\text{ = }}{{\left\| {\boldsymbol{L}} \right\|}_*}} , \\ \;\;\mathop {\lim }\limits_{\gamma \to 0} {\left\| {\boldsymbol{L}} \right\|_\gamma } = \mathop {\lim }\limits_{\gamma \to \infty } \displaystyle\sum\limits_i {\frac{{(1 + \gamma ){\sigma _i}({\boldsymbol{L}})}}{{\gamma + {\sigma _i}({\boldsymbol{L}})}}} {\text{ = }}\displaystyle\sum\limits_i {1{\text{ = rank(}}{\boldsymbol{L}}{\text{)}}} , \end{array} $

所以， $\gamma $ 范数比核范数更逼近秩函数。另外，为了进一步说明 $\gamma $ 范数的逼近度，本文给出了 $\gamma $ 范数（ $\gamma = $ $ 0.1$ , 0.01）和核范数的函数图形，如图1所示。从图1可以看到，本文提出的 $\gamma $ 范数比核范数更逼近秩函数，同时， $\gamma {\text{ = }}0.01$ 的逼近效果比 $\gamma {\text{ = }}0.1$ 更好，本实验中所用的 $\gamma {\text{ = }}0.01$ 。

于是，本文提出ITNN模型如下：

$ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{l} \mathop {{\text{min}}}\limits_{{\boldsymbol{L}}{\text{,}}{\boldsymbol{S}}} {\left\| {\boldsymbol{L}} \right\|_\gamma } - \mathop {\max }\limits_{_{{\boldsymbol{A}}{{\boldsymbol{A}}^{\text{T}}} = {\boldsymbol{I}}, {\boldsymbol{B}}{{\boldsymbol{B}}^{\text{T}}} = {\boldsymbol{I}}}} {\text{tr}}\left( {{{\boldsymbol{A}}^{\text{T}}}{\boldsymbol{LB}}} \right){\text{ + }}\lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\text{s}}{\text{.t}}{\text{. }}\;\;\;\;{\boldsymbol{ M}}{\text{ = }}{\boldsymbol{L}}{\text{ + }}{\boldsymbol{S}} \end{array} } $

(5)

1.2 改进的截断核范数模型求解

由式（5）得ITNN模型含待求解项 $\mathop {\max }\limits_{_{{\boldsymbol{A}}{{\boldsymbol{A}}^{\text{T}}} = {\boldsymbol{I}}, {\boldsymbol{B}}{{\boldsymbol{B}}^{\text{T}}} = {\boldsymbol{I}}}} {\rm{tr}} \left( {{{\boldsymbol{A}}^{\text{T}}}{\boldsymbol{LB}}} \right)$ ，故式（5）需要分为以下两个步骤进行求解。

步骤1：给定 $ {{\boldsymbol{L}}^k} $ 对 $ {{\boldsymbol{L}}^k} $ 进行奇异值分解即 $ [{{\boldsymbol{U}}^k},{{\boldsymbol{\varSigma}} ^k}, $ $ {{\boldsymbol{V}}^k}] = SVD({{\boldsymbol{L}}^k}) $ ，得到 $ {{\boldsymbol{L}}^k} $ 对应的左、右奇异向量如下：

$ \begin{array}{l} {{\boldsymbol{U}}^k}{\text{ = }}({u_1},{u_2}, \cdots ,{u_m}) \in {{\mathbb{R}}^{m \times m}} , \\ {{\boldsymbol{V}}^k}{\text{ = }}({v_1},{v_2},\cdots,{v_n}) \in {{\mathbb{R}}^{n \times n}} 。\end{array} $

并通过取对应的前r个左、右奇异向量得到：

$ \begin{array}{l} {{\boldsymbol{A}}^k}{\text{ = }}({u_1},{u_2},\cdots,{u_r}) \in {{\mathbb{R}}^{m \times r}} , \\ {{\boldsymbol{B}}^k}{\text{ = }}({v_1},{v_2}, \cdots ,{v_r}) \in {{\mathbb{R}}^{m \times r}} 。\end{array} $

步骤2：在步骤1的基础上求解优化问题：

$ \begin{array}{l} ({{\boldsymbol{L}}^{k + 1}},{{\boldsymbol{S}}^{k + 1}}) = \mathop {\arg \min }\limits_{{\boldsymbol{L}},{\boldsymbol{S}}} {\left\| {\boldsymbol{L}} \right\|_\gamma } - {\rm{tr}}\left( {{{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}} \right) + \lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\text{s}}{\text{.t}}{\text{.}}\;\;\;\;\;{\boldsymbol{M}} = {\boldsymbol{L}} + {\boldsymbol{S}}\\[-22pt] \end{array} $

(6)

本文采用GADMM算法求解式（6）所示的优化问题，其对应的增广拉格朗日函数为：

$ \begin{aligned}[b] \varPhi ({\boldsymbol{L}},{\boldsymbol{S}},{\boldsymbol{Y}},\mu ) =& {\left\| {\boldsymbol{L}} \right\|_\gamma } - {\rm{tr}}\left( {{{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}} \right) + \lambda {\left\| {\boldsymbol{S}} \right\|_1} - \\ &\left\langle {{\boldsymbol{Y}},{\boldsymbol{L}} + {\boldsymbol{S}} - {\boldsymbol{M}}} \right\rangle + \dfrac{\mu }{2}\left\| {{\boldsymbol{L}} + {\boldsymbol{S}} - {\boldsymbol{M}}} \right\|_{\rm{F}}^2 \end{aligned} $

(7)

式中， $ {\boldsymbol{Y}} $ 为拉格朗日乘子， $ \;\mu > 0 $ 为惩罚参数， $ {\Vert ·\Vert }_{{\rm{F}}}^{} $ 是Frobenius范数。通过以下步骤对问题（6）进行求解：

首先，固定 $ {{\boldsymbol{S}}^t} $ 、 $ {{\boldsymbol{Y}}^t} $ 和 $ {\mu _t} $ ，更新 $ {{\boldsymbol{L}}^{t + 1}} $ ，即

$ \begin{aligned}[b] {{\boldsymbol{L}}^{t + 1}} =& \mathop {\arg \min }\limits_{\boldsymbol{L}} {\text{ }}\varPhi ({\boldsymbol{L}},{{\boldsymbol{S}}^t},{{\boldsymbol{Y}}^t},{\mu _t}) = \\ &\mathop {\arg \min }\limits_{\boldsymbol{L}} {\left\| {\boldsymbol{L}} \right\|_\gamma } - {\rm{tr}}\left( {{{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}} \right) - \\ &\left\langle {{{\boldsymbol{Y}}^t},{\boldsymbol{L}} + {{\boldsymbol{S}}^t} - {\boldsymbol{M}}} \right\rangle + \dfrac{{{\mu _t}}}{2}\left\| {{\boldsymbol{L}} + {{\boldsymbol{S}}^t} - {\boldsymbol{M}}} \right\|_{\rm{F}}^2 = \\ &\mathop {\mathop {\arg \min }\limits_{\boldsymbol{L}} }\limits_{} {\left\| {\boldsymbol{L}} \right\|_\gamma } + \\ &\dfrac{{{\mu _t}}}{2}\left\| {{\boldsymbol{L}} - \left({\boldsymbol{M}} - {{\boldsymbol{S}}^t} + \dfrac{{{{\boldsymbol{Y}}^t} + {{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}}}{{{\mu _t}}}\right)} \right\|_{\rm{F}}^2 \end{aligned} $

(8)

由文献[14]可知，为了求解式（8），可以转化为优化问题 $ \mathop {{\text{min}}}\limits_{\boldsymbol{Z}} F({\boldsymbol{Z}}) + \dfrac{\mu }{2}\left\| {{\boldsymbol{Z}} - {\boldsymbol{D}}} \right\|_{\rm{F}}^2 $ 进行求解。其中， $ F({\boldsymbol{Z}}){\text{ = }} $ $ f(\sigma ({\boldsymbol{Z}})) $ ，上述优化问题的解为 $ {{\boldsymbol{Z}}^*} = {\boldsymbol{U}}{\rm{diag}}({\sigma ^*}){{\boldsymbol{V}}^{\rm{T}}} $ 。其中， $ {\boldsymbol{U}}{\rm{diag}}({\sigma _{\boldsymbol{D}}}){{\boldsymbol{V}}^{\rm{T}}} $ 为 $ {\boldsymbol{D}} \in {{\mathbb{R}}^{{\boldsymbol{m}} \times {\boldsymbol{n}}}} $ 的奇异值分解，由此可以求得 $ {\sigma ^*} = pro{x_{f,\mu }}({\sigma _{\boldsymbol{D}}}) $ ， $ pro{x_{f,\mu }}({\sigma _{\boldsymbol{D}}}) $ 为Moreau–Yosida算子，其表达式为：

$ {\;\;\;\;\;\;\;\;\;\;\;\;\;pro{x_{f,\mu }}}({\sigma _{\boldsymbol{D}}}): = \mathop {\arg \min }\limits_{\sigma \ge 0} f(\sigma ) + \frac{\mu }{2}\left\| {\sigma - {\sigma _{\boldsymbol{D}}}} \right\|_2^2 $

(9)

式（9）可以用凸规划差分（difference of convex，DC）算法^[14]进行求解。

于是，得到式（8）的最优解为：

$ {{\boldsymbol{L}}^{t + 1}} = {\boldsymbol{U}}{\rm{diag}}({\sigma ^*}){{\boldsymbol{V}}^{\rm{T}}} $

(10)

式中， $ {\sigma ^*} $ 为当 $ {\boldsymbol{D}} = {\boldsymbol{M}} - {{\boldsymbol{S}}^t} + \dfrac{{{{\boldsymbol{Y}}^t} + {{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}}}{{{\mu _t}}} $ 时，采用DC算法求解问题（9）的 $ \sigma $ 的局部最优解点。

其次，固定 $ {{\boldsymbol{L}}^{t + 1}} $ 、 $ {{\boldsymbol{Y}}^t} $ 和 $ {\mu _t} $ ，更新变量 $ {{\boldsymbol{S}}^{{{{\boldsymbol{t}} + }}1}} $ ，即

$ \begin{aligned}[b] {{\boldsymbol{S}}^{t + 1}} =& \mathop {\arg \min }\limits_{\boldsymbol{S}} \varPhi ({{\boldsymbol{L}}^{t + 1}},{\boldsymbol{S}},{{\boldsymbol{Y}}^t},{\mu _t}) = \\ &\mathop {{\text{ }}\arg \min }\limits_{\boldsymbol{S}} {\text{ }}\lambda {\left\| {\boldsymbol{S}} \right\|_1} - \left\langle {{{\boldsymbol{Y}}^t},{\boldsymbol{S}}} \right\rangle + \\ &\frac{{{\mu _t}}}{2}\left\| {\alpha {{\boldsymbol{L}}^{t + 1}} - (1 - \alpha )({{\boldsymbol{S}}^t} - {\boldsymbol{M}}) + {\boldsymbol{S}} - {\boldsymbol{M}}} \right\|_{\rm{F}}^2 = \\ &\mathop {\arg \min }\limits_{\boldsymbol{S}} \frac{\lambda }{{{\mu _t}}}{\left\| {\boldsymbol{S}} \right\|_1}\; + \\ &\frac{1}{2}\left\| {{\boldsymbol{S}} - [{\boldsymbol{M}} - \alpha {{\boldsymbol{L}}^{t + 1}} + (1 - \alpha )({{\boldsymbol{S}}^t} - {\boldsymbol{M}}) + \frac{{{{\boldsymbol{Y}}^t}}}{{{\mu _t}}}]} \right\|_{\rm{F}}^2 \end{aligned} $

(11)

式中， $ \alpha \in (0,2) $ 为松弛因子。当 $ \alpha {\text{ = 1}} $ 时，GADMM算法退化为经典的ADMM算法。可以利用软阈值收缩算子对式（11）的变量 $ {{\boldsymbol{S}}^{t + 1}} $ 进行更新，得到迭代格式如下：

$ {\;\;\;\;\;\;\;{\boldsymbol{S}}^{t + 1}} = \;{\varTheta _{\frac{\lambda }{{{\mu _t}}}}}\left[{\boldsymbol{M}} - \alpha {{\boldsymbol{L}}^{t + 1}} + (1 - \alpha )({{\boldsymbol{S}}^t} - {\boldsymbol{M}}) + \frac{{{{\boldsymbol{Y}}^t}}}{{{\mu _t}}}\right] $

(12)

式中， $ {\varTheta _\xi }( \cdot ) $ 为软阈值收缩算子，定义为 $ {\varTheta _\xi }({\boldsymbol{E}}) = $ $ \max (|{\boldsymbol{E}}| - \xi ,0) \cdot {{\rm{sign}}} ({\boldsymbol{E}}) $ ，其中， $ \xi > 0 $ 为参数， $ {{\rm{sign}}} ( \cdot ) $ 为符号函数。

最后，固定 $ {{\boldsymbol{L}}^{t + 1}} $ 、 $ {{\boldsymbol{S}}^{{{t + }}1}} $ ，更新拉格朗日乘子 $ {{\boldsymbol{Y}}^{t + 1}} $ 和惩罚因子 $ {\mu _{t + 1}} $ ：

$ {\;\;\;\;\;{\boldsymbol{Y}}^{t + 1}} = {\boldsymbol{Y}}{}^t - {\mu _t}[\alpha {{\boldsymbol{L}}^{t + 1}} - (1 - \alpha )({{\boldsymbol{S}}^t} - {\boldsymbol{M}}) + {{\boldsymbol{S}}^{t + 1}} - {\boldsymbol{M}}] $

(13)

$ {\mu _{t + 1}} = \min \left( {\rho {\mu _t},{\mu _{\max }}} \right) $

(14)

式中，ρ为放大系数。

综上所述，使用算法1、2求解问题（5）。

算法1 　求解问题（5）的总算法

1）初始化： $ {{\boldsymbol{L}}^0}{\text{ = }}0 $ 。

2）给定 $ {{\boldsymbol{L}}^k} $ ，计算 $ {{\boldsymbol{L}}^k} $ 的奇异值分解：

$ [{{\boldsymbol{U}}^k},{{\boldsymbol{\varSigma}} ^k},{{\boldsymbol{V}}^k}] = SVD({{\boldsymbol{L}}^k}) , $

得到左、右奇异向量 $ {{\boldsymbol{U}}^k} $ 和 $ {{\boldsymbol{V}}^k} $ ，进而得到其分别对应的截断奇异向量 $ {{\boldsymbol{A}}^k} $ 和 $ {{\boldsymbol{B}}^k} $ 。

3）求解如下优化问题：

$ \begin{array}{l} ({{\boldsymbol{L}}^{k + 1}},{{\boldsymbol{S}}^{k + 1}}) = \mathop {\arg \min }\limits_{{\boldsymbol{L}},{\boldsymbol{S}}} {\left\| {\boldsymbol{L}} \right\|_\gamma } - {\rm{tr}}\left( {{{({{\boldsymbol{A}}^k})}^{\rm{T}}}{\boldsymbol{L}}{{\boldsymbol{B}}^k}} \right) + \lambda {\left\| {\boldsymbol{S}} \right\|_1} \\ {\rm{ s.t}}.\;\;\;\;\;{\boldsymbol{M}} = {\boldsymbol{L}} + {\boldsymbol{S}}\text{。} \end{array} $

4）若满足终止条件 $ \dfrac{{{{\left\| {{\boldsymbol{M}} - {{\boldsymbol{L}}^{k + 1}} - {{\boldsymbol{S}}^{k + 1}}} \right\|}_{\text{F}}}}}{{{{\left\| {\boldsymbol{M}} \right\|}_{\text{F}}}}} \le {10^{{{ - 4}}}} $ ，迭代终止；否则，令 $ k{\text{ = }}k{\text{ + 1}} $ 返回步骤2）。

下面给出采用GADMM算法求解算法1中步骤3）（问题（6））的具体算法2，。

算法2 　采用GADMM求解算法1中步骤3）的算法

1）初始化：给定参数 $ \lambda $ 、 $ \;\mu $ 、 $ \;\rho $ 的初值 $ \lambda > 0 $ ， $ \;{\mu _{\max }} > {\mu _{\text{0}}} > 0 $ ， $ \;\rho > 1 $ ；给定初始点 $ {{\boldsymbol{L}}_0}{\text{ = 0}} $ 、 $ {{\boldsymbol{S}}_0}{\text{ = 0}} $ 和 $ {{\boldsymbol{Y}}_0}{\text{ = }} $ $ \dfrac{{\boldsymbol{M}}}{{\max ({{\left\| {\boldsymbol{M}} \right\|}_2},\sqrt {mn} {{\left\| {\boldsymbol{M}} \right\|}_\infty })}} $ ；迭代次数 $ t = 0 $ 。

2）根据式（10）更新变量 $ {{\boldsymbol{L}}^{t + 1}} $ 。

3）根据式（12）更新变量 $ {{\boldsymbol{S}}^{t + 1}} $ 。

4）根据式（13）更新 $ {{\boldsymbol{Y}}^{t + 1}} $ 。

5）根据式（14）更新 $ {\;\mu _{t + 1}} $ 。

6）若满足终止条件 $ \dfrac{{{{\left\| {{\boldsymbol{M}} - {{\boldsymbol{L}}^{t + 1}} - {{\boldsymbol{S}}^{t + 1}}} \right\|}_{\text{F}}}}}{{{{\left\| {\boldsymbol{M}} \right\|}_{\text{F}}}}} \le {10^{{{ - 4}}}} $ ，迭代终止；否则，令 $ t = t + 1 $ ，返回步骤2）。

2 实验结果与分析

本文通过视频前背景分离试验验证ITNN算法的优势。实验中，采用的仿真软件为MATLAB R2018a，运行的计算机硬件环境为i5–5287U CPU@2.9 GHz，对比算法包括GDSS^[15]、MAMR^[20]、NNWNN^[12]、NonLRSD^[13]、TNN^[21]、GoDec^[15]和PCP^[8]算法。实验的对象为CDnet数据集^[26]和I2R数据集^[27]中的Airport、ShoppingMall、WaterSurface、Escalator、Curtain、Cubicle、Corridor和Car视频。ITNN算法的参数设置为 $ \;\rho {\text{ = 1}}{\text{.5}} $ ， $ {\;\mu _0}{\text{ = }}{\dfrac{{{\text{12}}}}{{\left\| {\boldsymbol{M}} \right\|}}_2} $ ， $ {\;\mu _{\max }}{\text{ = 1}}{{\text{0}}^{\text{7}}} $ ， $ \lambda {\text{ = }}\dfrac{1}{{\sqrt {\max (m,n)} }} $ ， $ \alpha {\text{ = }}0.1 $ ， $ \gamma {\text{ = }}0.1n $ 。

为了验证提出的ITNN算法的优势，以8个实验视频序列为实验对象，进行视频前背景分离仿真实验，并随机选取Airport视频的第1 656帧、ShoppingMall视频的第1 862帧、WaterSurface视频的第1 624帧、Escalator视频的第4 595帧、Curtain视频的第22 774帧、Cubicle视频的第1 303帧、Corridor视频的第817帧和Car视频的第689帧的实验效果进行分析，实验结果如图2所示。

从图2可以看出：本文提出的ITNN算法较其他对比算法具有更好的分离效果。例如：从Airport视频提取前景的效果（图2的第1行）可以看出，本文提出的ITNN算法提取的前景图片的中间偏右部分和中间偏上部分比其他对比算法的噪声更少。从对ShoppingMall视频提取前景的效果（图2的第2行）可以看出，ITNN算法提取的前景的右上角部分具有较少的噪声。从WaterSurface视频提取前景的效果（图2的第3行）可以看出，ITNN算法从视频中提取的人的轮廓信息更加丰富和完整，噪声更少；同等条件下，其他算法只能提取人轮廓的一半乃至更少的信息，且提取的前景所包含的噪声较多，产生噪声最明显的是Godec算法。从Curtain视频提取前景的效果（图2的第5行）可以看出，ITNN算法提取的前景中人的信息较丰富，尤其是比TNN算法提取的人的信息丰富，并且比GDSS、MAMR、NNWNN、NonLRSD、Godec和PCP算法产生的噪声更少。综上所述，从视觉角度来看，本文提出的ITNN算法与其他对比算法相比提取的前景效果更好，前景信息更丰富和完整。

为了进一步定量分析ITNN算法的优势，本文引入了F-measure值。F-measure值是用于评价视频前背景分离效果的一个重要量化指标，其表达式为： $ F = \dfrac{{2RP}}{{R + P}} $ 。其中： $ P = \dfrac{{{t_{\rm{p}}}}}{{{t_{\rm{p}}} + {f_{\rm{p}}}}} $ 为精确率，表示正确检测出的前景像素个数与视频序列中所有被检测到的像素的占比； $ R{\text{ = }}\dfrac{{{t_{\rm{p}}}}}{{{t_{\rm{p}}} + {f_{\rm{n}}}}} $ 为召回率，表示正确检测出的前景像素个数与视频序列中所有前景像素的占比； $ {t_{\text{p}}} $ 是被正确的分类为前景像素的个数； $ {f_{\text{n}}} $ 是前景像素被错判为背景像素的个数； $ {f_{\text{p}}} $ 是将背景像素错判为前景像素的个数。F-measure值的范围介于0与1之间，数值越大则表明算法对应的视频前背景分离效果越好。

ITNN算法与上述7种对比算法进行视频前背景分离的F-measure值如表1所示。表1的最后一行给出了每种算法在视频前背景分离过程中的平均F-measure值。

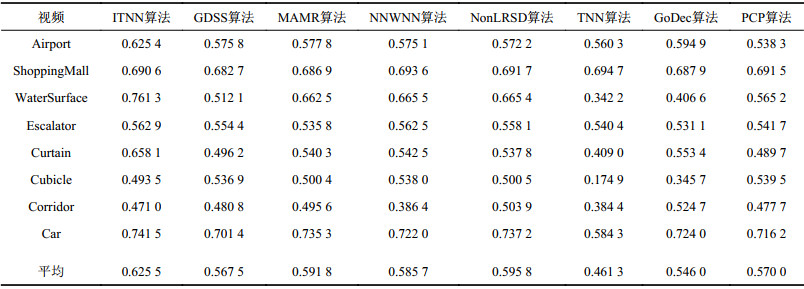从表1可以看出：ITNN算法在对Airport、WaterSurface、Escalator、Curtain和Car进行视频前背景分离的F-measure值较其他对比算法更高。例如，对Airport视频，ITNN算法的F-measure值比PCP算法高9%；对WaterSurface视频，ITNN算法的F-measure值比TNN算法高42%；对Escalator视频，ITNN算法的F-measure值比Godec算法高3%；对Curtain视频，ITNN算法的F-measure值比Godec算法高12%；对Car视频，ITNN算法的F-measure值比TNN算法高12%。平均F-measure值最高的为本文提出的ITNN算法，比次高的NonLRSD算法高3%，比最低的TNN算法高12%，也即本文提出的ITNN算法比其他7种基于RPCA的视频前背景分离算法的效果更好，从而定量地验证了提出的ITNN算法的优越性。

为了验证ITNN算法的时间复杂度，实验记录了ITNN算法与上述7种对比算法进行视频的前背景分离的运行时间，如表2所示。

从表2中的平均时间可以看出：由于GoDec算法使用了加速算法，所以其运行时间最快；除GoDec算法外，ITNN算法的平均运行时间只比GDSS算法略慢，但比其他5种算法要快，其中，比MAMR算法快0.18 s/帧，比NNWNN算法快0.02 s/帧，比NonLRSD算法快0.017 s/帧，比TNN算法快0.5 s/帧，比PCP算法快0.3 s/帧。进一步验证了ITNN算法在时间复杂度上的优势。

综上所述，本文从视觉和量化（即F-measure值和运行时间）两个角度验证了提出的ITNN算法的优越性。

3 结　论

以截断核范数方法为代表的传统鲁棒主成分分析方法中的核范数对鲁棒主成分分析模型中的秩函数逼近程度不高，进而影响到视频前背景分离的效果。在此背景下，本文提出了一种改进的截断核范数（ITNN）算法模型，该模型采用逼近程度较高的非凸 $\gamma $ 范数代替TNN算法模型中的核范数，同时，从理论上分析了非凸 $\gamma $ 范数与核范数对秩函数的逼近度，并采用GADMM算法对提出的模型进行求解。将该模型应用于视频前背景分离实验中，从实验结果的视觉角度可以看到本文提出的ITNN算法具有较好的视频前背景分离效果。另外，实验中记录了ITNN及其对比算法对不同视频前背景分离的F-measure值和运行时间。ITNN的平均F-measure值为0.625 5，平均运行时间为0.076 0 s/帧，进一步验证了本文提出的ITNN算法模型的有效性和优越性。但是，本文提出的ITNN算法仍然不是最优的秩函数的替代函数，寻找更优的替代函数仍然是下一步研究工作的重点。