2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050;
3. 甘肃建筑职业技术学院,甘肃 兰州 730050;
4. 中铁二十局集团市政工程有限公司,甘肃 兰州 730030
2. Western Center of Disaster Mitigation in Civil Eng. of Ministry of Education, Lanzhou Univ. of Technol., Lanzhou 730050, China;
3. Gansu Vocational College of Architecture, Lanzhou 730050, China;
4. China Railway Construction 20th Group Municipal Corp., Lanzhou 730030, China
管翼缘焊接箱型截面构件作为一种新型组合构件,逐渐被人们认识和使用,但是其设计理论仍未完善。管翼缘焊接箱型截面构件包括管翼缘焊接箱型截面组合梁和管翼缘焊接箱型截面组合柱。管翼缘组合梁是将传统钢–混凝土组台梁中工字钢梁的平钢板上翼缘用钢管混凝土替代,而形成的一种新型组合结构构件。近年来,由于管翼缘组合梁良好的刚度和稳定性,多应用于大跨度桥梁工程。这种管翼缘组合梁的应用,不仅使得桥梁的跨度更大,而且使得整体桥梁质量向更轻的方向发展。桥梁因处于不同的地质环境条件,其中的梁和柱构件常常存在腐蚀等耐久性问题。为保证结构的安全性和耐久性,提出用耐候钢替代普通结构钢应用于桥梁结构当中。同时,由于市场及地域等诸多因素限制,工程中常用焊接钢管代替无缝钢管,这种情况要求更高的焊缝质量。因此,研究不同焊缝熔深下的焊接箱型截面构件的承载力性能意义重大。
为了使钢管混凝土构件更好地应用于实际工程中,国内外学者一直致力于钢管混凝土构件的性能研究。吕西林等[1]通过试验研究了轴心受压方钢管混凝土短柱的破坏机理、延性和极限承载力,讨论了不同钢管宽厚比以及混凝土强度等级对方钢管混凝土短柱性能的影响。韩林海等[2]利用数值解法计算出方钢管混凝土轴心受压时的荷载–变形全过程关系曲线,并进行了试验研究,推导出轴压强度和轴压模量等参数的简化计算公式。Kuranovas等[3]对1 303个钢管混凝土试件的试验数据进行了分析,并与欧洲标准EC4中确定这些组合构件承载能力的方法进行了比较,给出了一些典型的曲线图以供研究人员对比使用。Chang等[4]介绍了一种新型组合构件—不锈钢–碳素钢管混凝土柱,并进行了一系列的抗压试验,提出了修正的混凝土芯材应力应变模型,对碳素钢管的管厚、管径和屈服强度等参数进行了研究,明确组合柱的性能。Yu等[5]在针对目前钢管混凝土柱的设计实践中,对于不同的截面采用不同的计算公式进行轴向承载力计算的问题,提出了圆截面和多边形截面实心和空心钢管混凝土柱轴心承载力的统一计算公式。Romero等[6]研究了超高强混凝土对圆钢管混凝土的影响,通过细长柱试验的结果对欧洲规范EC4中关于组合柱设计的现行规定进行了评估。丁发兴[7]、傅强[8]等结合试验和有限元方法分析比较耐候钢管混凝土轴压短柱与普通钢管混凝土轴压短柱力学性能的差异,结果表明耐候钢管混凝土轴压短柱静力力学性能与钢管混凝土试件无显著差异。Yu等[9]对15根再生自密实钢管混凝土(recycled self-compacting concrete filled steel tubular,RSCCFST)柱进行了轴压试验,根据试验研究和极限平衡理论,推导了钢管混凝土柱承载力的计算公式;在此基础上,提出了钢管混凝土柱极限应变、刚度和应力应变关系的预测模型。为了进一步提高钢管混凝土短柱轴压承载力计算的准确性,曹兵等[10]收集和整理了国内外562个钢管混凝土短柱轴压承载力试验数据,结果表明,《钢管混凝土结构技术规范》(GB 50936—2014)[11]计算模型的理论计算值相比于试验值多数偏高。唐红元等[12]通过研究圆不锈钢管混凝土柱轴压承载力,由拟合公式推导得出圆不锈钢管混凝土抗压承载力模型。
对于钢管混凝土短柱在局部受压下的受力性能及其承载力的影响因素,目前仅开展了有限的研究。刘威等[13]通过对28个方钢管混凝土轴压短构件局压承载力的试验研究,提出了方钢管混凝土局压承载力的初步计算方法。Ding等[14]通过试验对圆钢管混凝土短柱和方形钢管混凝土短柱在局部受压下的受力性能进行研究,并提出了钢管混凝土短柱局部受压承载力的解析计算公式。Yang等[15–16]研究了矩形截面的深宽比、部分受压面积比(混凝土截面与部分受压面积之比)、顶端板的钢板厚度、部分受压的承压板形状(矩形和条形)对局压短柱受力性能的影响。
国内外学者对钢管混凝土翼缘组合梁的研究较少,其中Sause等[17]对钢管混凝土翼缘工字形钢梁(concrete-filled tubular flange girders,CFTFGs)的受力性能进行了试验研究,试验结果表明,CFTFGs的侧向扭转屈曲能力得到提高,在施工工况和最终施工工况下均具有较好的承载设计荷载的能力,为工程设计提供了参考。郑霜杰[18]系统研究了圆钢管混凝土翼缘组合梁的受力性能,分析圆钢管混凝土翼缘–组合梁破坏机理,其在桥梁工程中的应用具有一定的技术经济性。计静等[19]进行矩形钢管混凝土翼缘–蜂窝钢腹板H形截面组合短柱轴压性能试验研究。
本文依托西北地区兰州某大跨度钢结构高架桥梁中矩形焊接管翼缘组合梁中构件设计施工时的具体问题,研究在实际施工过程中高空泵送混凝土的压力对焊接耐候钢管焊缝的影响及承载力问题。在研究钢管混凝土承载力性能时,由于加载装置的荷载显著小于钢管混凝土理论承载力,故在试验中设计了局部受压的加载方式以测得试件极限承载力。试验结果为局部加载的工程情况(例如,人行天桥支座下部柱端的局部加载受力情况)提供参考。试验考虑耐候钢焊接组合截面焊缝熔深因素,探究在不同熔深下的箱形焊接管翼缘组合构件的承载力性能及在单轴压力下的应力分布规律,并与理论计算值进行对比。
1 试验研究由于兰州地区某大跨度钢结构高架管翼缘组合桥梁中的构件多暴露在大气环境中,或者处于复杂的地区环境下,其必然存在防腐蚀的耐久性要求,故采用耐候钢代替普通结构钢。考虑实际工程中钢管混凝土管翼缘构件中翼缘主要承受压力的受力特点,设计了钢管混凝土柱构件的单轴压力试验。试验在兰州理工大学结构试验室进行,试验共加工制作3个试件,矩形钢管材料选用Q345qENH耐候钢,耐候钢的焊接材料具有耐候性能,钢管内浇C50自密实混凝土。
1.1 试件设计试验中,加工制作试件3个,分别为全熔透焊缝(14 mm)、部分熔透焊缝(8和11 mm)焊接箱型截面钢管混凝土短柱,柱截面尺寸为250 mm×500 mm,高度1 000 mm,钢板厚14 mm,如图1所示。试件尺寸及编号详见表1。在一些实际工程中,对钢管构件多设横向隔板等措施,以保证构件的稳定性和强度,而本工程的构件截面尺寸不大,仅为250 mm×500 mm,且内部填充混凝土,稳定性和强度有一定保证,所以未设置横向隔板。
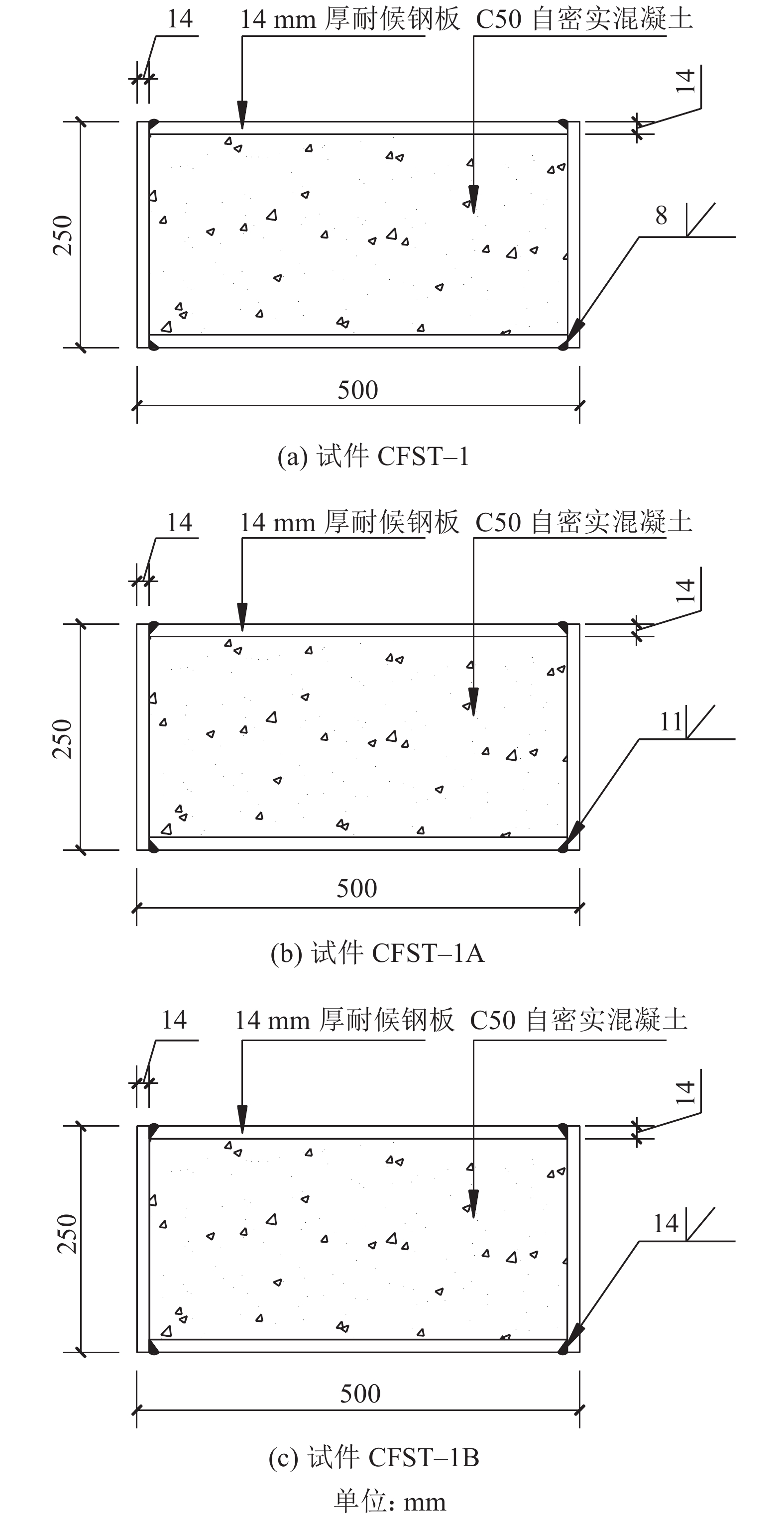 |
| 图1 试件横截面图 Fig. 1 Cross section of test specimens |
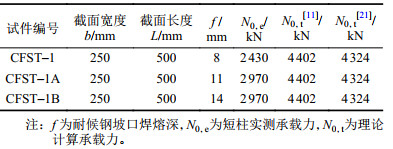
| 表1 轴心受压试件参数 Tab. 1 Parameters of axial compression specimens |
 |
1.2 材料力学性能
耐候钢采用Q345qENH级钢,制作加工3个标准试样,试样尺寸和拉伸试验结果见表2。试验耐候钢具有明显的弹性、屈服、强化和颈缩阶段。试验测得C50自密实混凝土7、15和30 d的标准立方体抗压强度分别为45、50和58.2 MPa,符合《混凝土结构设计规范》(GB50010—2010(2015年局部修订))[20]要求。
| 表2 耐候钢试件参数 Tab. 2 Parameters of weathering steel specimens |
 |
1.3 试验方案
试验通过两台200 t(型号为YAW–2000)的门式竖向加载装置连接一根横梁,并由一台500 t(型号为QF500T–20)的分离式油压千斤顶加载。试验过程中,液压千斤顶的荷载通过置于试件上端正中的局压钢垫板施加于试件,用两个位移计直接对称地支顶在加载垫块上部的钢板上表面,局压垫板相对于试件的位移由DH3816数据采集系统采集,加载示意如图2所示。
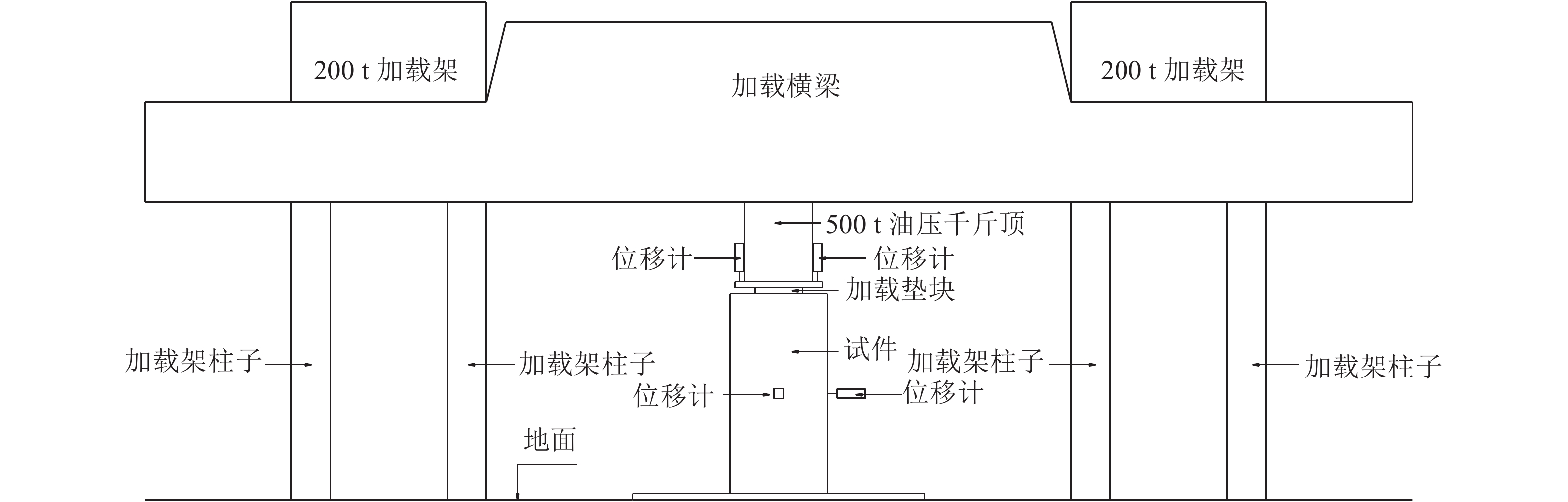 |
| 图2 试件加载示意图 Fig. 2 Schematic diagram of specimen loading |
1.3.1 测点布置及装置
为了测得受压钢管混凝土短柱的破坏模式及传力路径,试验分别测试混凝土内部应变及耐候钢表面的应变。电阻应变片型号为BX120–3AA。在浇筑混凝土前,对贴在钢筋上的电阻应变片使用环氧树脂胶作为防水处理。在混凝土短柱内部中心位置(试件高度为500 mm处)放置3根相互垂直的钢筋并进行绑扎固定,3根钢筋长度分别为150、300和500 mm。每根钢筋两端分别贴1片应变片,共计6片应变片(1~6),具体布置如图3所示。在耐候钢表面一共粘贴36片应变片,其中:28个点(7~34)测试静态应变(1~28);其他8个点(D1~D8)测试动态应变,以找寻峰值应变以及应变变化规律,具体布置如图4所示。同时,在试件长边对称位置竖向放置2个量程50 mm的位移计(L1、L2),用以测量竖向位移;在长边(L3)及短边(L4)竖向中心位置水平放置2个量程50 mm的位移计用以测量横向位移;位移传感器型号为WY–50,灵敏度为200 με/mm,具体布置如图5所示。静态应变及位移由DH3816静态应变测试分析系统采集,动态应变由INV3060V动态采集仪采集。图6为试验加载现场照片。
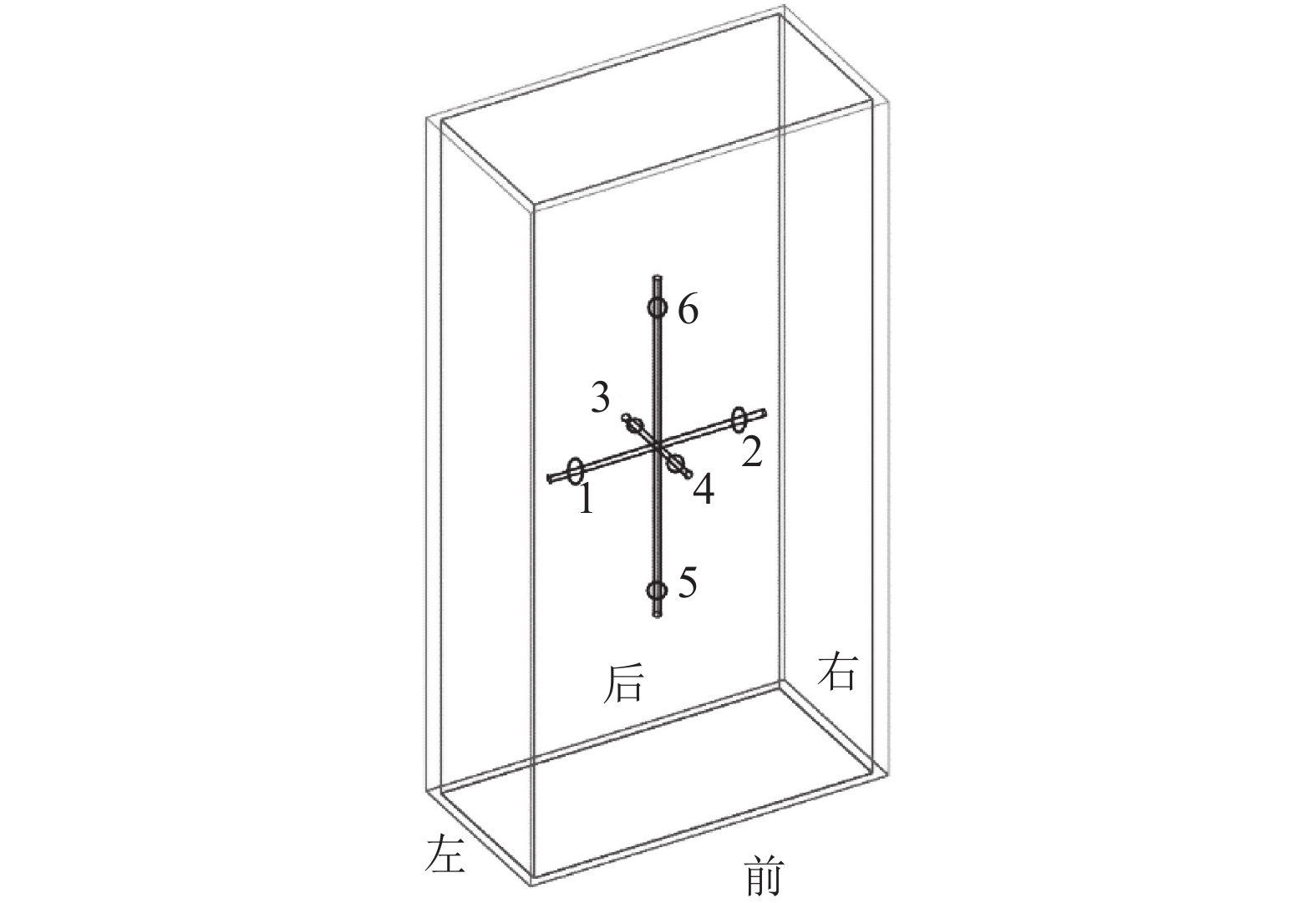 |
| 图3 混凝土内部应变片布置 Fig. 3 Layout of strain gauges inside concrete |
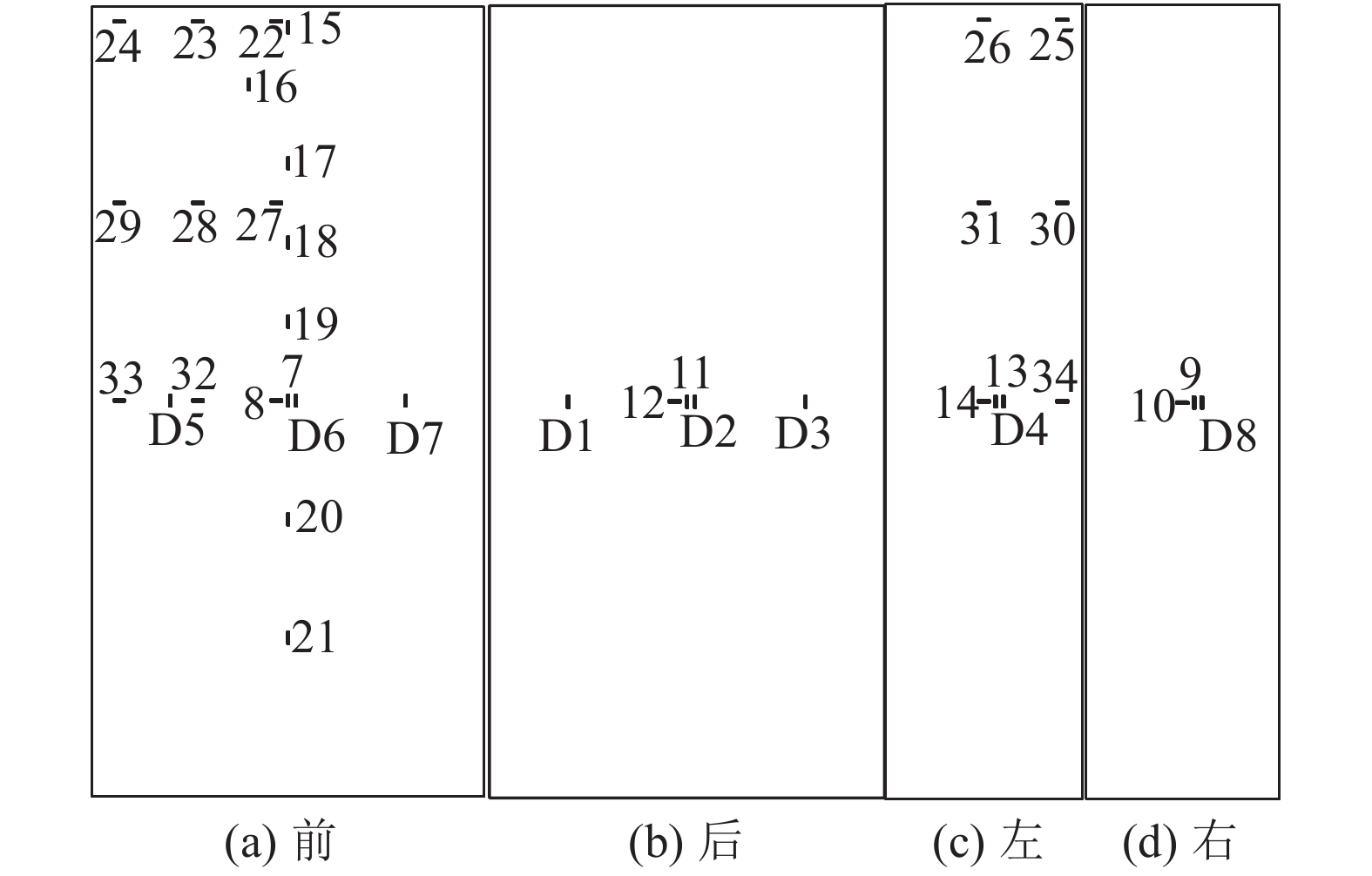 |
| 图4 试件表面应变片布置 Fig. 4 Layout of strain gauge on specimen surface |
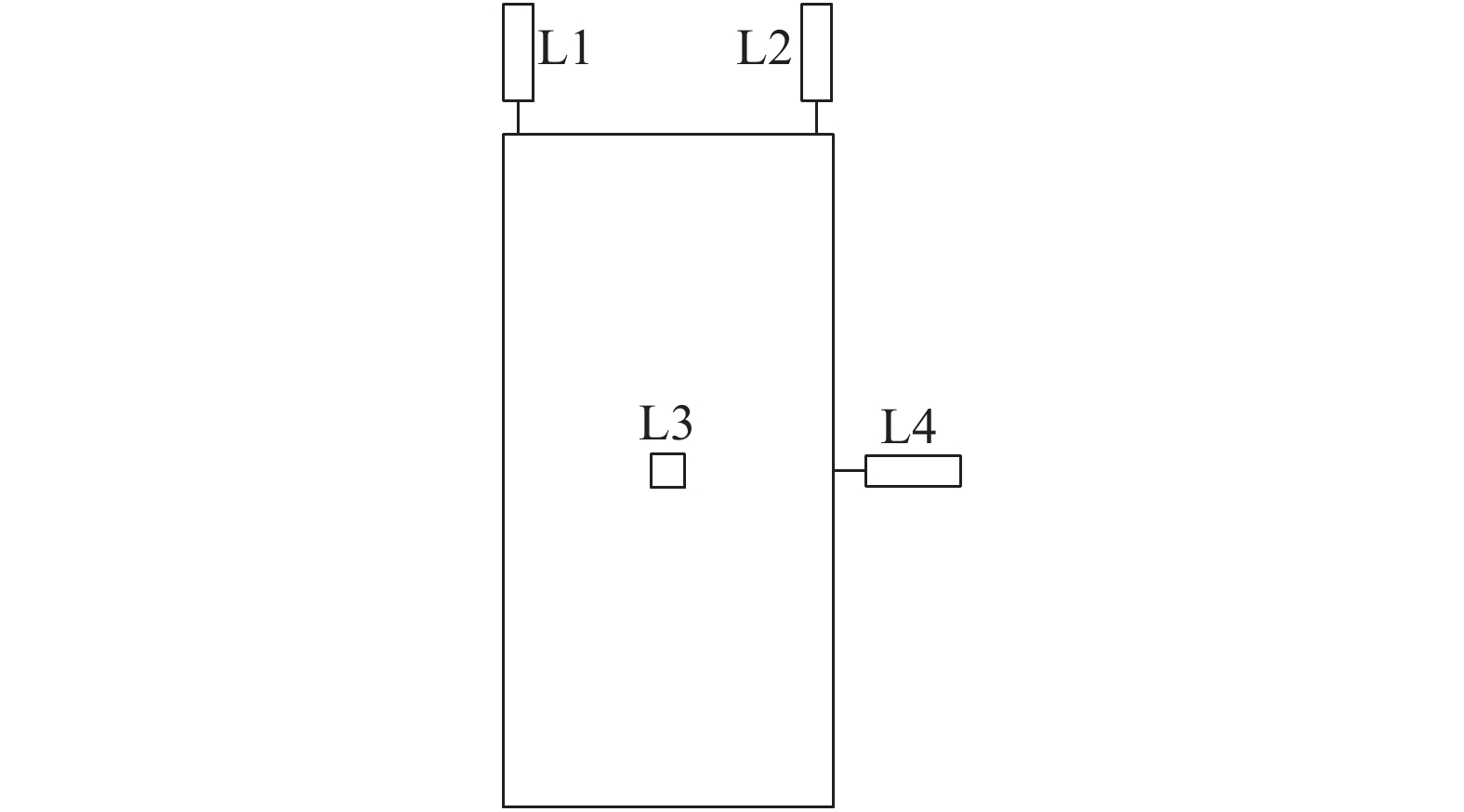 |
| 图5 位移传感器布置 Fig. 5 Layout of displacement sensor |
 |
| 图6 试验加载现场照片 Fig. 6 Photo of test loading site |
1.3.2 加载方案
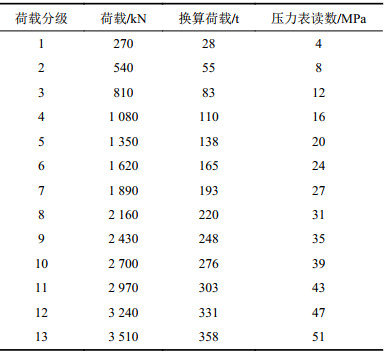
选用尺寸为245 mm×125 mm×30 mm的矩形钢板垫块进行局部加载,加载按照预估破坏荷载一共分13级进行,每级加载270 kN、5 min,持荷5 min,前3级光预加载再卸载。具体加载步骤及荷载换算如表3所示。
| 表3 加载步骤 Tab. 3 Loading steps |
 |
2 试验结果及分析 2.1 试件破坏过程及破坏形态
不同焊缝熔深的3个试件全部发生混凝土的局部剪切破坏,混凝土裂缝沿着局压垫块的4个角部斜向开展到矩形钢管焊接角部,混凝土开裂后的试件如图7所示。其中,对试件CFST–1B在混凝土开裂后继续加载,直至整个垫块陷入混凝土中,以测得混凝土开裂后钢管表面及混凝土内部应变的变化规律。3个试件均未发生整体的倾斜变形,只是在侧向发生局部鼓起。
 |
| 图7 3组试件破坏形态 Fig. 7 Failure modes of three groups of specimens |
由图7(a)可见,在荷载作用下,部分熔透的试件(熔深8 mm)钢板约束能力弱,钢管发生明显鼓起,塑性变形明显;由图7(b)可见,在荷载作用下,部分熔透的试件(熔深11 mm)钢板约束能力增大,钢管发生轻微鼓起;由图7(c)可见,在荷载作用下,全熔透的试件的混凝土套箍效应明显,混凝土能发挥较大承载力,箱型钢管也可承受一定荷载,两者组合效应明显。
由图7可见,随着熔深的增大,钢管的鼓起程度越小。对14 mm熔深的试件(图7(c)),在混凝土开裂后继续加载,可以看出钢板的鼓起程度加大了,说明全熔透的钢管混凝土试件在局压荷载下混凝土开裂后,钢管依然可以承受荷载并产生塑性变形。
由此可知,全熔透的试件对钢管内混凝土的约束作用最大,部分熔透的试件约束作用次之,故全熔透试件的钢管在混凝土开裂时的鼓起最小。
2.2 局压承载力由表1的3组试验的局压承载力可见,熔深增大到一定程度时,部分熔透试件和全熔透试件的承载力相等。
根据《钢管混凝土结构技术规范》(GB50936—2014)[11],钢管混凝土短柱的轴心受压强度承载力设计值N0按式(1)~(4)计算:
| ${N_0} = {A_{{\rm{sc}}}}{f_{{\rm{sc}}}}$ | (1) |
| ${f_{{\rm{sc}}}} = \left( {1.212 + B\theta + C{\theta ^2}} \right){f_{\rm{c}}}$ | (2) |
| ${\alpha _{{\rm{sc}}}} = \frac{{{A_{\rm{s}}}}}{{{A_{\rm{c}}}}}$ | (3) |
| $\theta = {\alpha _{{\rm{sc}}}}\frac{f}{{{f_{\rm{c}}}}}$ | (4) |
式中,
| ${N_{{\rm{ul}}}} = {N_0}\sqrt {\frac{{{A_{\rm{l}}}}}{{{A_{\rm{c}}}}}} $ | (5) |
式中,
同时,根据文献[21],参考式(6)计算钢管混凝土局压承载力折减系数KLC0为0.53,则根据
| ${K_{{\rm{LC0}}}} = A \cdot {\beta ^{ - 0.5}} + B$ | (6) |
式中,局压面积比
试验测得全熔透焊缝下的钢管混凝土局压承载力为2 970 kN,此结果明显低于理论计算值。说明根据规范[11]及文献[21]计算的局压承载力,结果会过高估计矩形焊接钢管混凝土的局压承载能力。
分析其原因,规范[11]提供的钢管混凝土的局压承载力是按照无缝圆钢管混凝土计算的,而本文是方钢管混凝土,一般情况下,圆形钢管混凝土的约束效应大于方钢管混凝土。而文献[21]提供的矩形钢管混凝土的承载力计算公式是由无缝钢管混凝土的试验及数值模拟得出,与本文的焊接钢管混凝土存在差异,说明焊接的钢管混凝土承载力相较于无缝钢管混凝土显著降低。
2.3 荷载位移曲线分析各试件的荷载位移曲线如图8~9所示。由图8可知:在混凝土开裂前试件的竖向位移随荷载的增大基本呈线性增长的趋势;同时,随着熔深的增大,竖向位移增大,且竖向两测点测得位移值相差不大,全熔透焊缝试件开裂时的竖向位移最大值为6.28 mm;在荷载达到一定程度时,不增加荷载的情况下位移继续增大;因试件CFST–1B开裂后继续加载,所测得的荷载位移曲线较完整,可以看出试件最终所能承受的荷载稳定在2 160 kN,试件开裂荷载即为构件所能承受的极限荷载。
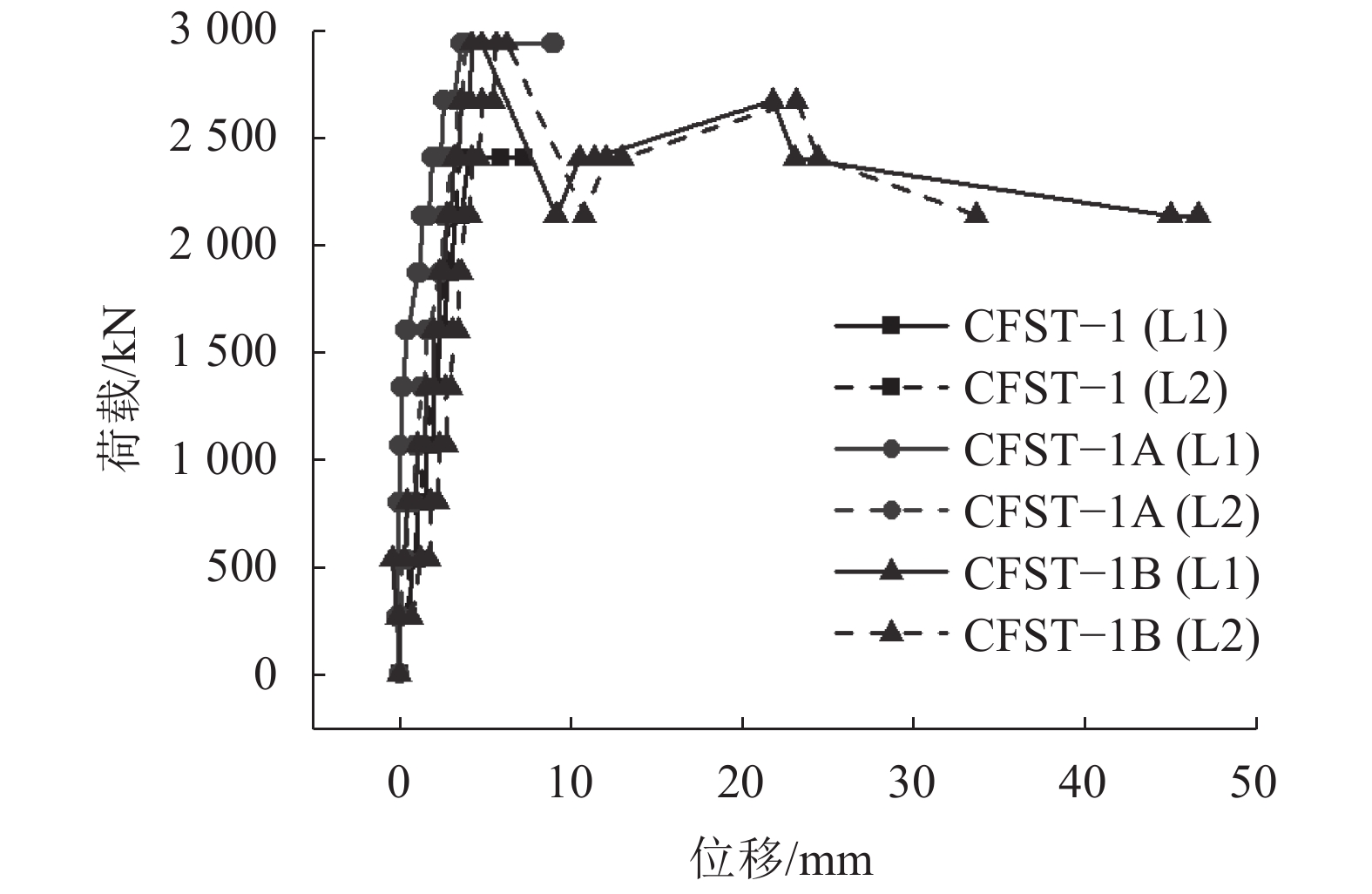 |
| 图8 试件竖向荷载位移曲线 Fig. 8 Vertical load displacement curves of specimens |
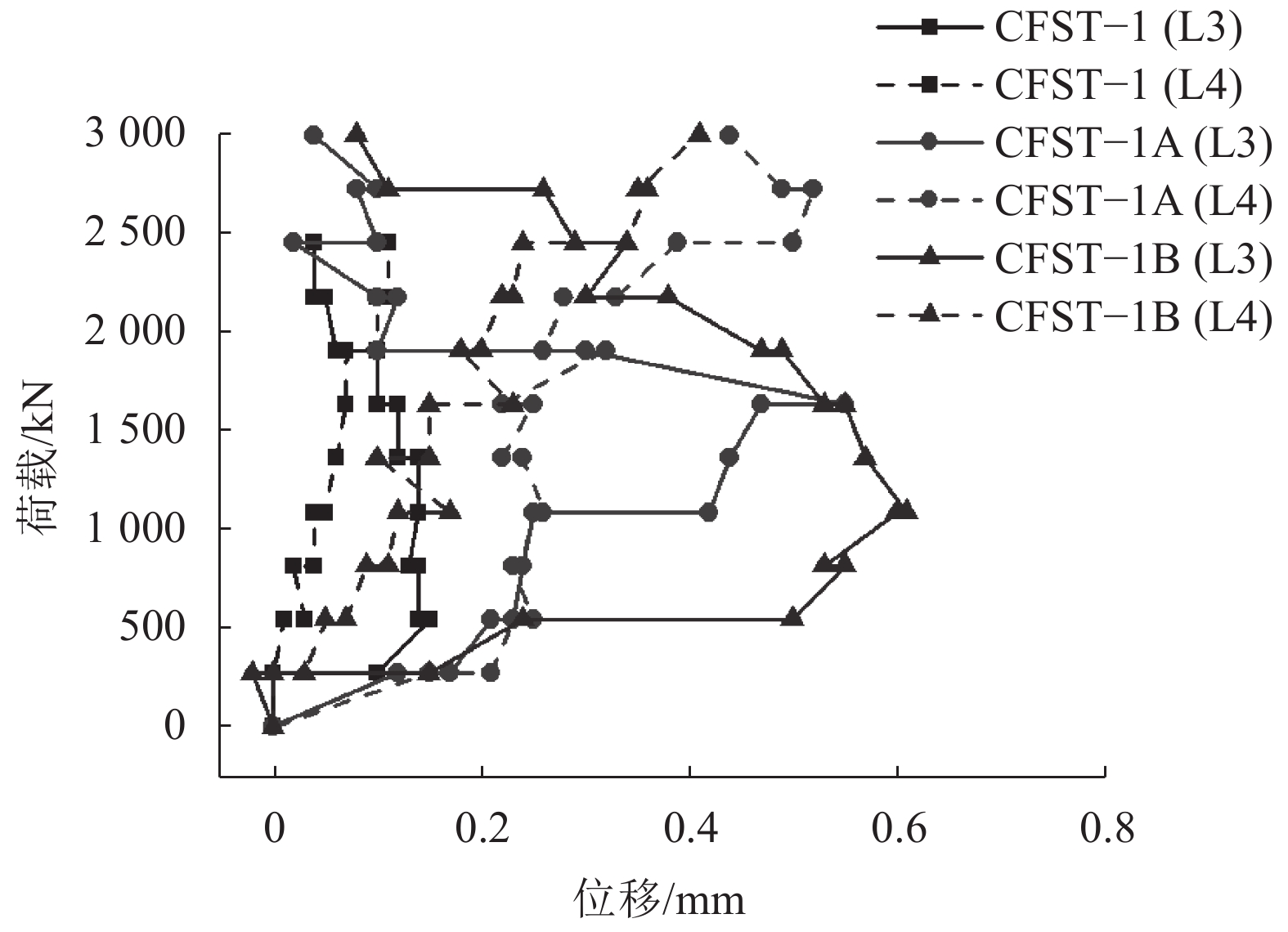 |
| 图9 试件横向荷载位移曲线 Fig. 9 Lateral load displacement curves of specimens |
从图9可知:3个试件右侧位移均呈现一个持续变大的过程;前侧位移整体呈先增长后减小的趋势,随着熔深的增大,前侧位移增大,全熔透焊缝试件前侧最大位移达到0.61 mm。由此可知3个试件侧向均发生局部鼓曲。
2.4 荷载应变曲线分析混凝土内部各测点的荷载应变曲线如图10所示。由于全熔透试件在浇灌混凝土时测点3和5应变片损坏,故只测得4个点的应变。从图10可以看出:部分熔透焊缝的试件在局压荷载下,混凝土内部测点竖向整体受压,中部横向基本呈现长向受拉、短向受压的受力状态,在混凝土开裂时应变发生突变;全熔透焊缝的试件3个方向都受压,混凝土开裂时应变突变不明显。以上分析说明全熔透焊缝的试件约束力大于部分熔透的试件,故部分熔透试件内部混凝土有横向膨胀的趋势。
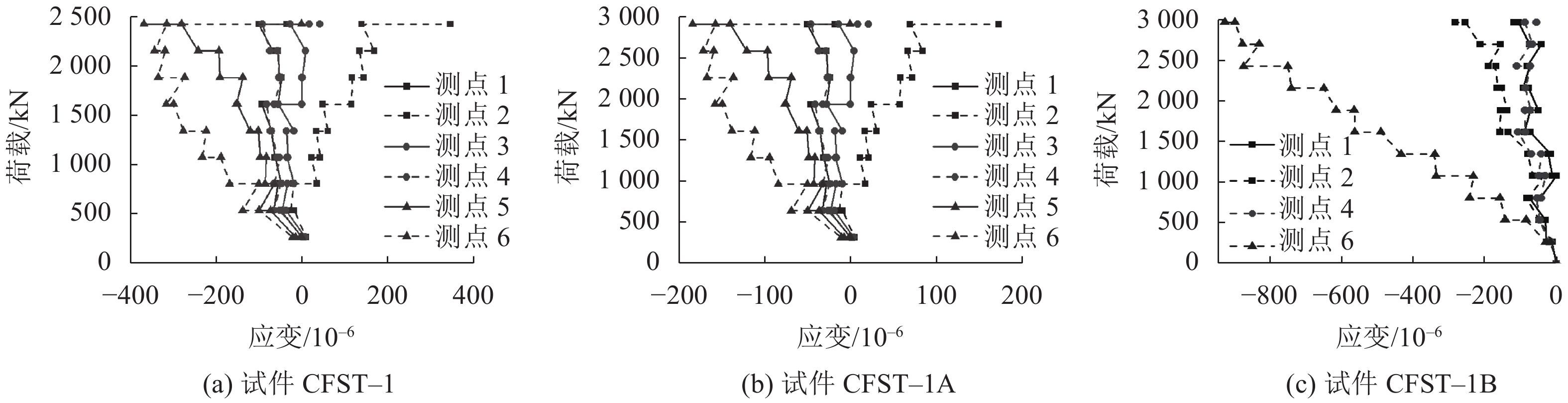 |
| 图10 混凝土内部荷载应变曲线 Fig. 10 Internal load strain curves of concrete |
钢材表面竖向荷载应变曲线如图11所示。
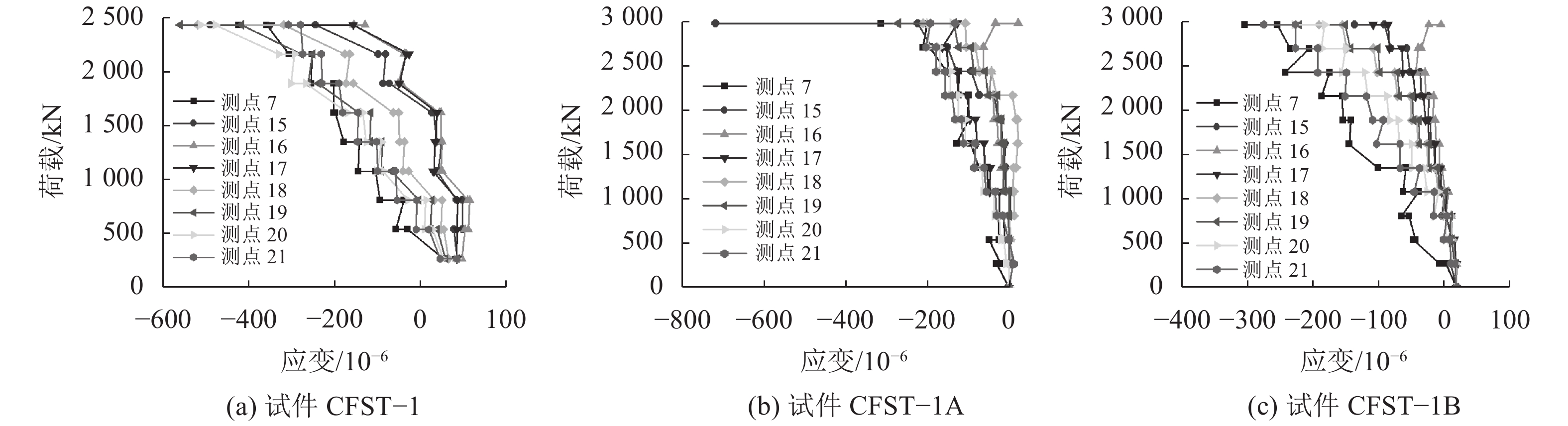 |
| 图11 钢材表面竖向荷载应变曲线 Fig. 11 Vertical load strain curve of steel surface |
由图11可以看出:直到混凝土压裂,耐候钢材一直处于弹性阶段,最大应变为720×10–6(试件CFST–1A),换算成应力为161 MPa。由此,即使混凝土已经开裂,钢管混凝土依然可以继续承受荷载并发生变形;3个试件竖向整体承受压应变,且随荷载增大呈增大的趋势,最大竖向应变在试件的中部位置,试件底部应变次之。由应变发展规律可知,局部鼓曲位置向试件底部发展,这与试验中观察到的钢材表面鼓曲一致。
钢材表面横向荷载应变曲线如图12所示。
 |
| 图12 钢材表面横向荷载应变曲线 Fig. 12 Lateral load strain curve of steel surface |
由图12可以看出:在钢管混凝土试件顶部,中间部位钢材横向受拉,四角部位钢材横向受压;在钢管混凝土试件中上部,表面横向整体受拉;在钢管混凝土试件中部,表面横向整体受拉,局部应变发生突变。整体横向应变随着位置的增高而增大,部分熔透试件开裂时横向应变突变较全熔透试件明显。
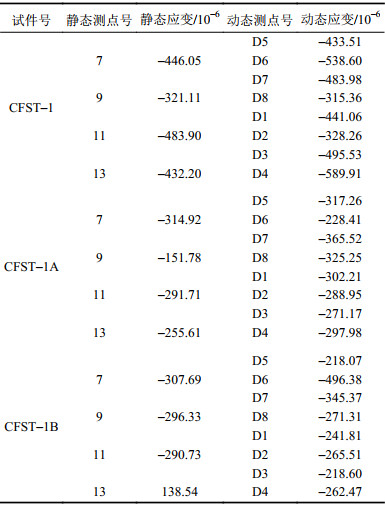
2.5 静态应变与动态应变分析对比试件中部同时刻的竖向静力与动力应变值如表4所示。由于篇幅所限,本文仅提供3种试件D5测点的动态应变时程曲线,如图13所示。
| 表4 静态与动态应变对比 Tab. 4 Comparison of static and dynamic strain |
 |
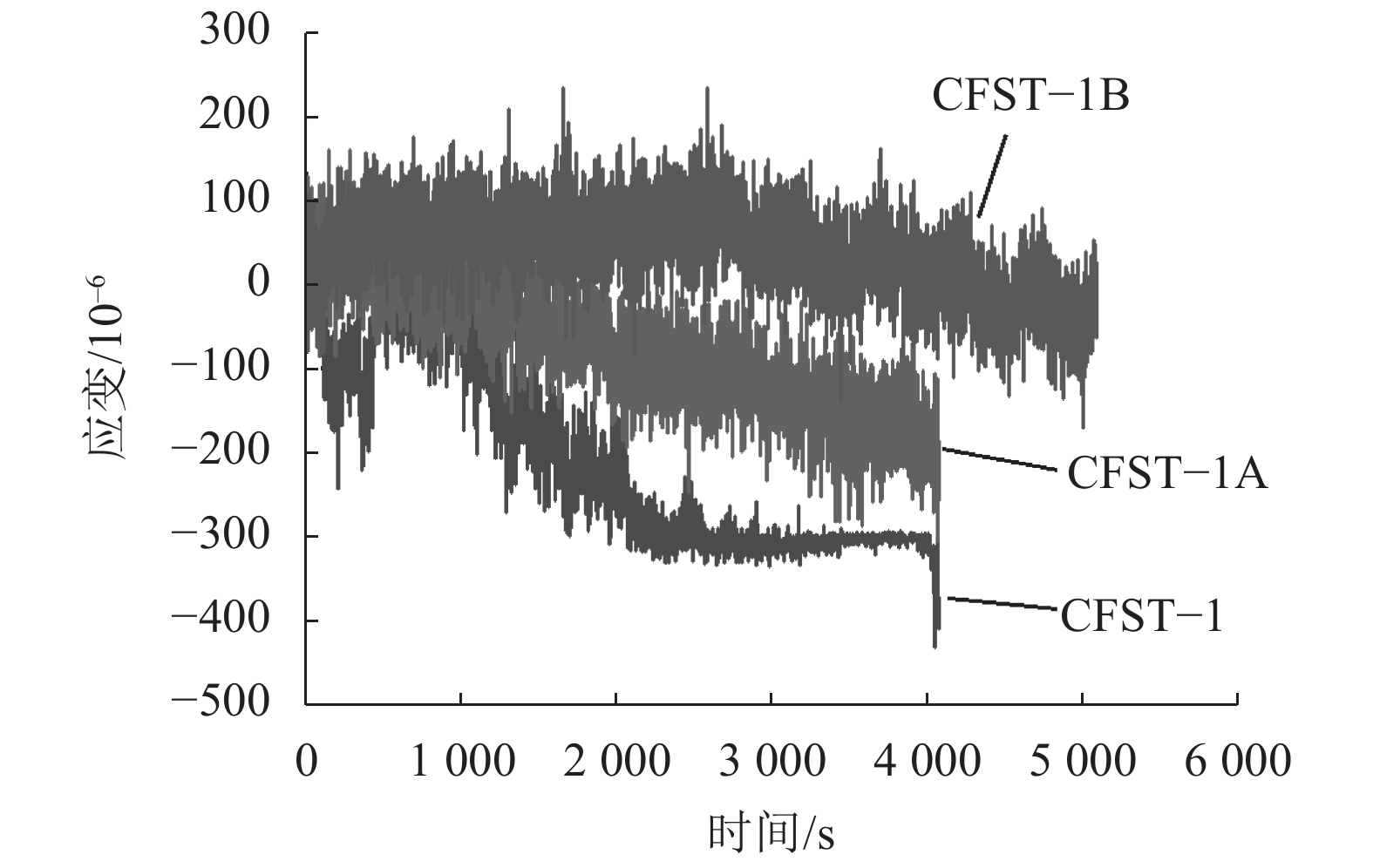 |
| 图13 试件测点D5动态应变时程曲线 Fig. 13 Dynamic strain time history curves of test point D5 |
由表4和图13可见,同时刻的静动态应变值相差不大,随着熔深的增大,D5测点的动态应变值整体呈减小的趋势。结果表明:全熔透试件的受力更合理,所测应变值更小。
3 结 论本文开展了焊接箱型截面构件在不同焊缝熔深下的局压单轴承载力试验,测得了试件位移变化及混凝土内部和钢管表面不同测点的静态及动态应变,得到以下主要结论:
1)所有试件均发生剪切破坏,随着试件熔深的增大,钢管的鼓起程度越小。混凝土开裂后,试件还能继续承受荷载并发生变形。
2)熔深达到一定程度后混凝土开裂时的部分熔透试件和全熔透试件竖向局压承载力相等。焊接矩形钢管混凝土试件承受单轴局压荷载下的开裂荷载即为构件所能承受的极限荷载。现有规范及文献提供的钢管混凝土局压承载力过高地估计了焊接矩形耐候钢管混凝土试件的承载能力。
3)全熔透试件在单轴压力作用下,开裂时的竖向位移较部分熔透试件的大,试件中部的横向鼓曲随荷载的增大而向试件底部延伸。
4)构件内部混凝土应变值,开裂时全熔透构件比部分熔透构件突变小。耐候钢表面最大竖向应变主要在试件的中部。试件横向整体受拉,局部在顶部角部位置受压,整体横向应变随着位置的增高而增大。
| [1] |
Lv Xilin,Yu Yong,Chen Yiyi,et al. Study on the performance of square concrete-filled steel tubular short column under axial compression:Ⅰ test[J]. Building Structure, 1999, 29(10): 41-43. [吕西林,余勇,陈以一,等. 轴心受压方钢管混凝土短柱的性能研究:Ⅰ试验[J]. 建筑结构, 1999, 29(10): 41-43. DOI:10.19701/j.jzjg.1999.10.008] |
| [2] |
Han Linhai,Tao Zhong. Study on behavior of concrete filled square steel tubes under axial load[J]. China Civil Engineering Journal, 2001, 34(2): 17-25. [韩林海,陶忠. 方钢管混凝土轴压力学性能的理论分析与试验研究[J]. 土木工程学报, 2001, 34(2): 17-25. DOI:10.3321/j.issn:1000-131X.2001.02.004] |
| [3] |
Kuranovas A,Goode D,Kvedaras A K,et al. Load-bearing capacity of concrete-filled steel columns[J]. Journal of Civil Engineering and Management, 2009, 15(1): 21-33. DOI:10.3846/1392-3730.2009.15.21-33 |
| [4] |
Chang X,Ru Z L,Zhou W,et al. Study on concrete-filled stainless steel carbon steel tubular (CFSCT) stub columns under compression[J]. Thin-Walled Structures, 2013, 63: 125-133. DOI:10.1016/j.tws.2012.10.002 |
| [5] |
Yu M,Zha X X,Ye J Q,et al. A unified formulation for circle and polygon concrete-filled steel tube columns under axial compression[J]. Engineering Structures, 2013, 49: 1-10. DOI:10.1016/j.engstruct.2012.10.018 |
| [6] |
Romero M L,Ibanez C,Espinos A,et al. Influence of ultra-high strength concrete on circular concrete-filled dual steel columns[J]. Structures, 2017, 9: 13-20. DOI:10.1016/j.istruc.2016.07.001 |
| [7] |
Ding Faxing,Fu Qiang,Fang Changjing. Research on the mechanical behavior of concrete -filled round-ended weathering steel tubular stub columns under axially compressive loading[J]. Journal of Railway Engineering Society, 2017, 34(11): 33-38. [丁发兴,傅强,方常靖. 圆端形耐候钢管混凝土轴压短柱力学性能研究[J]. 铁道工程学报, 2017, 34(11): 33-38. DOI:10.3969/j.issn.1006-2106.2017.11.008] |
| [8] |
Fu Qiang,Wang Liping,Fang Changjing. Behavior of concrete-filled rectangular weathering steel tubular stub columns under axially compressive loading[J]. Journal of Building Structures, 2017, 38(Supp1): 198-203. [傅强,王莉萍,方常靖. 矩形耐候钢管混凝土轴压短柱受力性能研究[J]. 建筑结构学报, 2017, 38(增刊1): 198-203. DOI:10.14006/j.jzjgxb.2017.S1.027] |
| [9] |
Yu F,Chen L,Bu S S,et al. Experimental and theoretical investigations of recycled self-compacting concrete filled steel tubular columns subjected to axial compression[J]. Construction and Building Materials, 2020, 248: 1-17. DOI:10.1016/j.conbuildmat.2020.118689 |
| [10] |
Cao Bing,Wang Yijun,Huang Bo,et al. Calculation model error and algorithm of axial compression bearing capacity for concrete-filled steel tubular stub columns[J]. Journal of Hefei University of Technology(Natural Science), 2020, 43(4): 512-521. [曹兵,王义俊,黄博,等. 钢管混凝土短柱轴压承载力计算模型误差及算法[J]. 合肥工业大学学报(自然科学版), 2020, 43(4): 512-521. DOI:10.3969/j.issn.1003-5060.2020.04.014] |
| [11] |
中华人民共和国住房和城乡建设部.钢管混凝土结构技术规范:GB50936—2014[S].北京:中国建筑工业出版社,2014.
|
| [12] |
Tang Hongyuan,Fan Luyao,Zhao Xin,et al. Bearing capacity model of circular concrete-filled stainless steel stub columns under uniaxial compression[J]. Advanced Engineering Sciences, 2020, 52(3): 10-20. [唐红元,范璐瑶,赵鑫,等. 圆不锈钢管混凝土短柱轴压承载力模型研究[J]. 工程科学与技术, 2020, 52(3): 10-20. DOI:10.15961/j.jsuese.201901101] |
| [13] |
Liu Wei,Han Linhai. Tests on local compression behaviors of axially loaded concrete-filled steel tubular members with square sections[J]. Industrial Construction, 2004, 34(1): 10-13. [刘威,韩林海. 方钢管混凝土轴压短构件局压承载力试验研究[J]. 工业建筑, 2004, 34(1): 10-13. DOI:10.3321/j.issn:1000-8993.2004.01.003] |
| [14] |
Ding F X,Liu J,Liu X M,et al. Mechanical behavior of circular and square concrete filled steel tube stub columns under local compression[J]. Thin-Walled Structures, 2015, 94: 155-166. DOI:10.1016/j.tws.2015.04.020 |
| [15] |
Yang Y F,Han L H. Experiments on rectangular concrete-filled steel tubes loaded axially on a partially stressed cross-sectional area[J]. Journal of Constructional Steel Research, 2009, 65(8): 1617-1630. DOI:10.1016/j.jcsr.2009.04.004 |
| [16] |
Yang Y F,Han L H. Concrete filled steel tube (CFST) columns subjected to concentrically partial compression[J]. Thin-Walled Structures, 2012, 50(1): 147-156. DOI:10.1016/j.tws.2011.09.007 |
| [17] |
Sause R,Kim B G,Wimer M R. Experimental study of tubular flange girders[J]. Journal of Structural Engineering-Asce, 2008, 134(3): 384-392. DOI:10.1061/(asce)0733-9445(2008)134:3(384) |
| [18] |
Zheng Shuangjie.Application research on the steel and concrete composite beam bridge with concrete filled tubular up-flange[D].Xi’an:Chang’an University,2010. 郑霜杰.圆钢管混凝土翼缘——组合梁桥应用研究[D].西安:长安大学,2010. |
| [19] |
Ji Jing,Xu Zhichao,Jiang Liangqin,et al. Experimental study on compression behavior of H-shaped composite short column with rectangular CFST flanges and honeycombed steel web subjected to axial load[J]. Journal of Building Structures, 2019, 40(9): 63-73. [计静,徐智超,姜良芹,等. 矩形钢管混凝土翼缘–蜂窝钢腹板H形截面组合短柱轴压性能试验研究[J]. 建筑结构学报, 2019, 40(9): 63-73. DOI:10.14006/j.jzjgxb.2018.0515] |
| [20] |
中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB50010—2010(2015年局部修订)[S].北京:中国建筑工业出版社,2015.
|
| [21] |
Liu Wei.Research on mechanism of concrete-filled steel tubes subjected to local compression[D].Fuzhou:Fuzhou University,2005. 刘威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学,2005. |
 2021, Vol. 53
2021, Vol. 53


