人类作为自然界长期进化的高等生物,在结构和功能上有着许多独特的优越性,如人臂的安全性、柔顺性、运动灵活性等。把人体的相关特性应用到机器人的研究中,不仅可以使机器人的结构和功能产生质的飞跃,还可以帮助仿人机器人更好地融入人类社会生活并与人类进行高效、友好的沟通协作[1]。拟人机械臂的仿人运动研究在仿人机器人中占有重要的地位,它的技术成熟与否直接决定机器人能否胜任复杂而精细的操作任务[2]。
目前,对于拟人臂仿人运动规划的研究大致可以分为两类:一类是基于指标的方法,建立人臂臂姿指标,通过对指标的优化来达到目的。其中,应用较广的是由心理物理学演化而来的不舒适度指标[3],该指标表明当关节角越远离中心角时,人就越感到不舒适。除此之外,学者们通过建立其他不同类型的指标来进行拟人臂的仿人运动。Zhao等[4]提出了一种基于能量指标的方法来进行臂姿的预测,该能量指标包括重力势能和弹性势能。甘亚辉等[5]利用人体工程学中的快速上肢评价指标来选定符合人类操作特点且满足性能要求的拟人臂构型。一些学者采用多目标函数融合的方式进行臂姿的预测。Chevtchenko等[6]在不舒适度指标的基础上,融合了关节位移、势能变化等其他指标,利用多指标加权的方式进行运动的预测。另一类是基于特性的方法,提取人臂运动特性,并将其融入到仿人运动规划中。这一类方法主要以人臂的某些特殊运动为研究对象,通过成千上百次的实验数据采集,利用如回归模型等数据算法对实验数据进行整合分析,归纳出人臂运动模型并使机械臂自主生成仿人运动[7]。其中,应用较为普遍的是肘部旋转角及其演化算法,通过建立人臂三角形实现拟人臂的仿人运动[8]。
无论是基于指标还是基于特性的方法,都存在不可避免的缺陷。在基于指标的研究中,单一指标往往不能满足仿人运动的需要,而多指标体系由于权重系数的影响,又存在很多不确定性。在基于特性的研究中,尽管有很多方法能够提取人臂臂姿特性,但是这些特性的准确性还有待进一步的验证。此外,这些特性大部分只是人臂所呈现出的表面现象,并不能反映人臂运动的真正内在机理。随着计算机技术及人工智能技术的发展,越来越多的新颖算法被应用到拟人臂的仿人运动中,例如,神经网络算法、贝叶斯网络算法等[9-10]。尽管这些算法能够帮助拟人臂产生类人化的手臂运动,但是往往忽略了手臂模型对运动精度的影响。人类的手臂运动是十分复杂的,运动过程中手臂的状态并不是一成不变的,不同的关节数和关节组合构成了不同的运动状态[11-12]。
针对人臂运动相似性及多样性特点[13],作者提出一种基于动作基元的人臂运动表达方式,能够直观反映人臂运动的内在机理。运动模型的多样化也能降低权重系数对整个运动精度的影响。此外,不同于传统动作基元基于某种特定任务的建立模式,该表达方式可以涵盖人臂的各种运动。同时,动作基元的特点可以有效、直接地建立人臂运动与拟人臂仿人运动之间的映射关系。根据不同基元的特点,建立对应的反解算法,使拟人臂能够满足仿人运动的要求。
1 手臂运动特点及运动学模型人臂运动主要依靠关节,其结构由上至下依次由肩关节、肘关节和腕关节连接而成。其主要运动方式为肩部的外展/内收、弯曲/伸展和肱骨的旋转、肘部的弯曲/伸展,以及小臂的旋前/旋后、腕部的外展/内收和腕部的弯曲/伸展。
采用的拟人臂实验平台为人形机器人NAO。NAO的每只手臂具有5个自由度,其中,肩关节3自由度,肘关节1自由度,腕关节1自由度,明确的生理关节配置使其可以应用到仿人运动规划中。
如图1所示,以右臂为例,采用D–H参数[14]描述拟人臂连杆之间的关系。
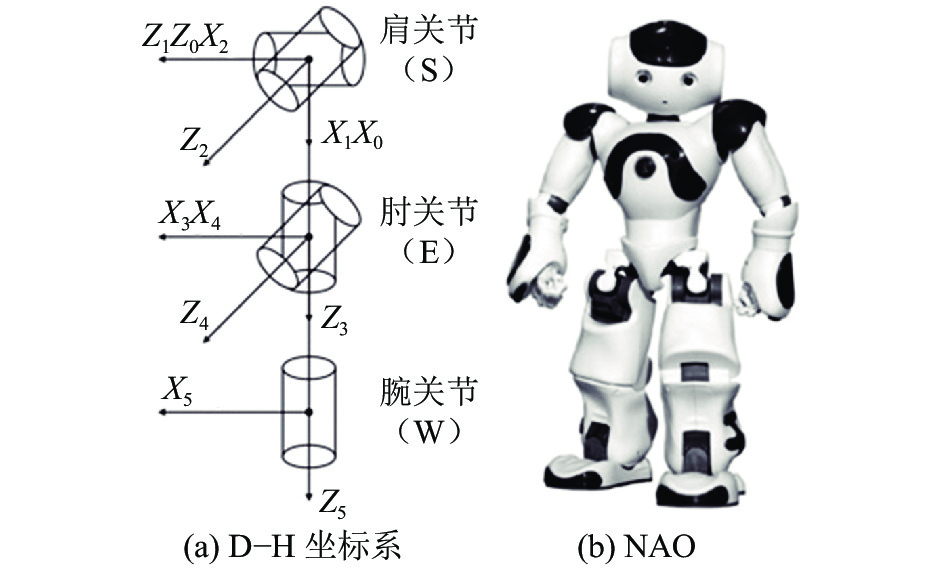 |
| 图1 D–H坐标系和人形机器人NAO Fig. 1 D–H coordinate and humanoid robot NAO |
D–H参数如表1所示,其中,nu、nl、nh分别表示NAO大臂、小臂以及手掌的长度。
| 表1 NAO手臂D–H参数 Tab. 1 D–H parameters of the NAO arm |
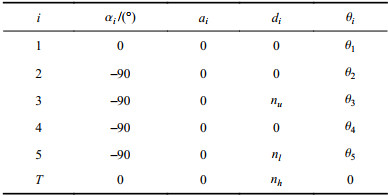 |
2 基于动作基元的运动表达
神经生理学研究表明:脊椎动物和无脊椎动物的运动都是由动作基元组成的[15]。通过动作基元的排列与重组完成运动的表达与实现。目前在机器人领域,动作基元也得到了广泛的应用。最主要的两个特点是减少计算量和模块化思想。特别是冗余度机器人,在智能学习及运动构成等方面有明显的优势[16]。
2.1 核心动作基元库人体结构可以以生理关节为基本单位,通过树状图的形式描述。如图1(a)所示,S、E、W3个节点分别表示人臂生理关节中的肩关节(父节点Parent)、肘关节(子节点Child)和腕关节(子孙节点Descendant)。根据人臂运动特点,每一个节点拥有两种属性:姿态属性(R)和位置属性(P)。姿态属性表示生理关节姿态的变化;位置属性表示生理关节位置的变化。图2为节点属性的详细信息。本文基于各个生理关节的属性,设定5种核心动作元素:SR、EP、ER、WP、WR。这5种动作元素分别对应了不同生理关节的不同属性变化,如SR表示肩关节姿态属性的变化,EP表示肘关节位置属性的变化。
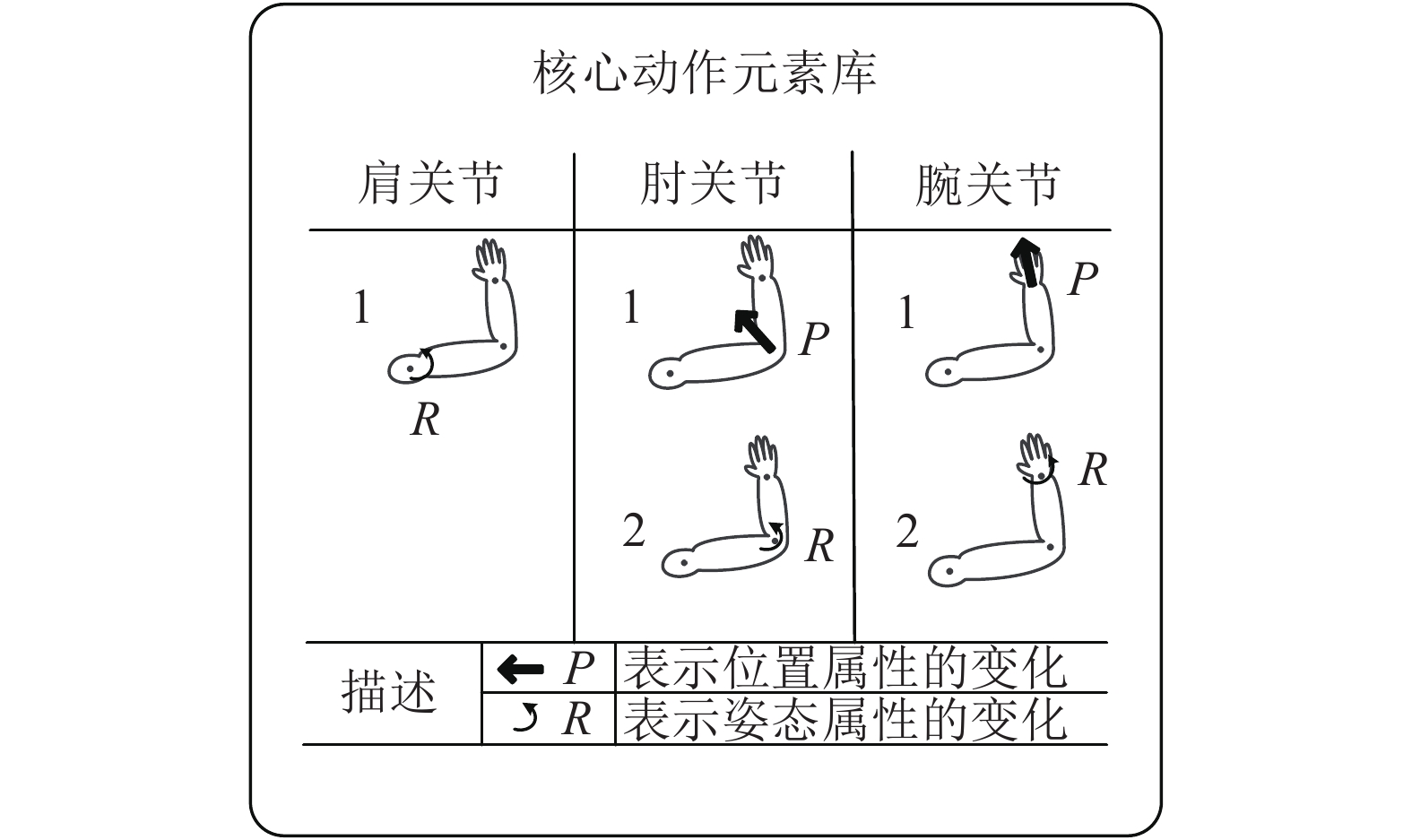 |
| 图2 各关节属性示意图 Fig. 2 Attributes of different joints |
2.2 动作基元的提取法则
根据手臂节点属性,驱动关节会发生姿态改变,并引起下层从动关节位置属性的变化,而从动关节的位置属性并不会主动改变。具体的提取法则如下:
1)父节点(S)固定在坐标系原点,其位置不会发生变化,因此肩关节只有姿态属性会发生变化。
2)姿态属性的变化是相对于父节点的,而位置属性的变化是相对于世界坐标系的。
3)通常,父节点姿态属性的变化会引起子节点位置属性的变化,即:
| $ {\rm{Paren}}{{\rm{t}}}_{R}\xrightarrow{\quad\quad}{\rm{Chil}}{{\rm{d}}}_{P}:{\rm{Paren}}{{\rm{t}}}_{R}{\rm{Chil}}{{\rm{d}}}_{P}。$ |
4)当且仅当父节点姿态属性的变化无法引起子节点位置属性的变化时,隔代影响将发生,即:
| $ {{\rm{Parent}}}_{R}\xrightarrow{\quad\quad}{{\rm{Child}}}_{P}:{{\rm{Parent}}}_{R}{{\rm{Desendant}}}_{P}。$ |
根据法则及串并联形式,共提取10种动作基元,如表2所示。这些动作基元根据运动类型可以分为两类:运动型和功能型。运动型动作基元描述的是末端位置发生变化的手臂自然运动;功能型动作基元描述的是末端位置不变的特殊运动,如避障、自运动等。主要关注的是运动型动作基元,文中的动作基元也泛指运动型动作基元。
| 表2 动作基元 Tab. 2 Movement primitives |
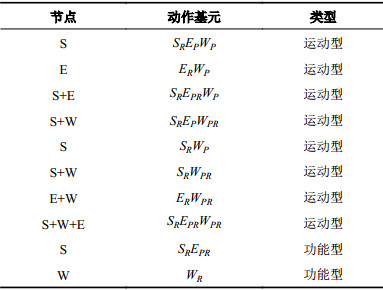 |
表2中,节点指主动发生变化的各生理关节,即姿态属性发生变化的关节。需要注意的是,根据拟人机械臂平台的结构不同,各动作基元所包含的自由度也有所不同。建立动作基元的方法不仅适用于常见的7自由度拟人臂,对于具有生理关节(肩关节、肘关节、腕关节)配置的多自由度拟人臂同样适用。
以动作基元SREPRWP为例,简单介绍表2中动作基元的物理意义。节点S+E表示肩关节和肘关节的姿态属性发生了主动变化,为驱动关节。其中,肩关节姿态属性的变化引起了肘关节位置属性的改变,而肘关节姿态属性的变化又引起了腕关节位置属性的改变。该动作基元描述的运动主要由肩关节和肘关节驱动完成,腕关节进行随动。该运动类似于达点运动,即不考虑腕部姿态的变化。
2.3 动作基元间的连接形式根据动作的定义,动作的初始和结束状态都是静止的,并且每个动作都具有明确的意义。因此,不同于动作元素的连接方式,动作基元之间只能进行串行连接。串行连接中最后一个动作基元往往是目标关键位姿,对动作的理解有时仅仅与最终的关键位姿有关。图3为动作基元连接简图。图3中:黑色圆圈表示不同的动作基元;从A到N代表基元执行顺序;实心箭头代表使能关系,即箭头前段的基元为箭头后端的基元做准备;空心箭头表示修饰关系;每个基元都可以通过不同的语义函数E(x)进行修饰,从而丰富该基元的表现形式[17];不同基元之间通过决策函数F(x)来进行选取和连接。根据不同动作基元的组合连接,可以构成丰富多样的仿人运动,从而满足不同任务的需求。
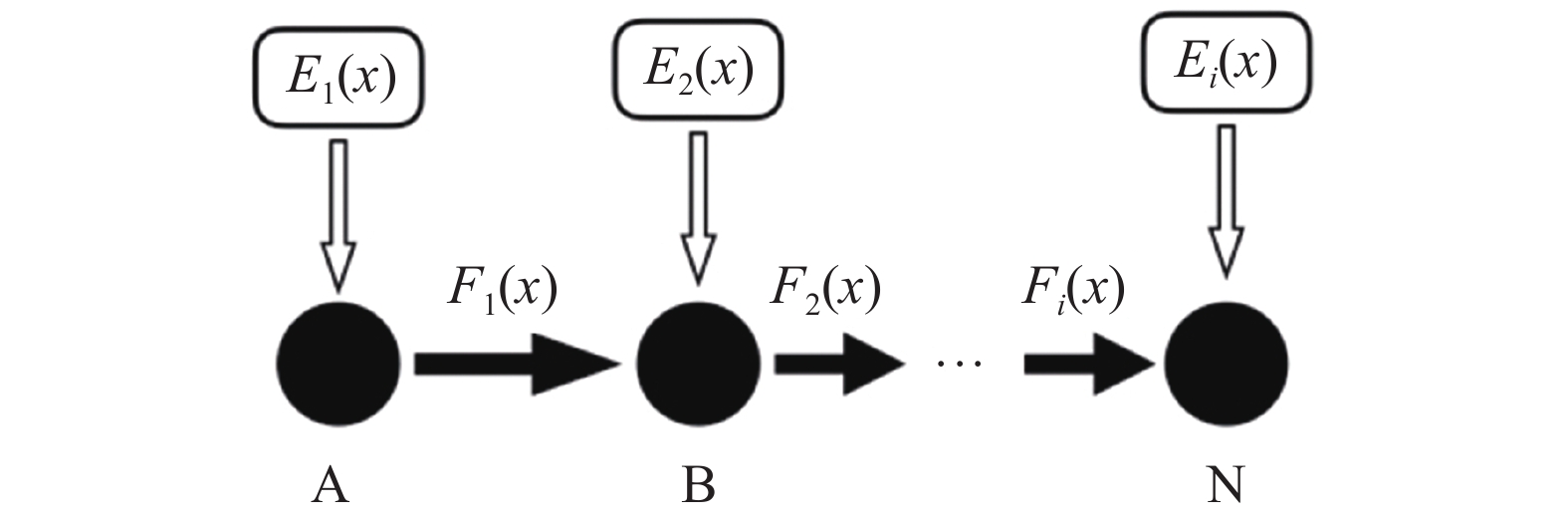 |
| 图3 动作基元连接简图 Fig. 3 Connection diagram of movement primitives |
2.4 基于动作基元的运动框架
提出一种基于动作基元的拟人臂仿人运动框架,如图4所示。该框架由4部分组成:智能决策层、子运动层、控制层及任务层。智能决策层是仿人运动规划的基础,动作基元是智能决策层的基础。从智能决策层到任务层自左向右的过程是对具体任务进行规划设计的过程,而从任务层到智能决策层自右向左的过程是对任务进行分解学习重构的过程。此外,通过接口与不同拟人臂的连接,该框架可实现不同拟人臂平台的仿人运动任务,从而实现框架的通用性。
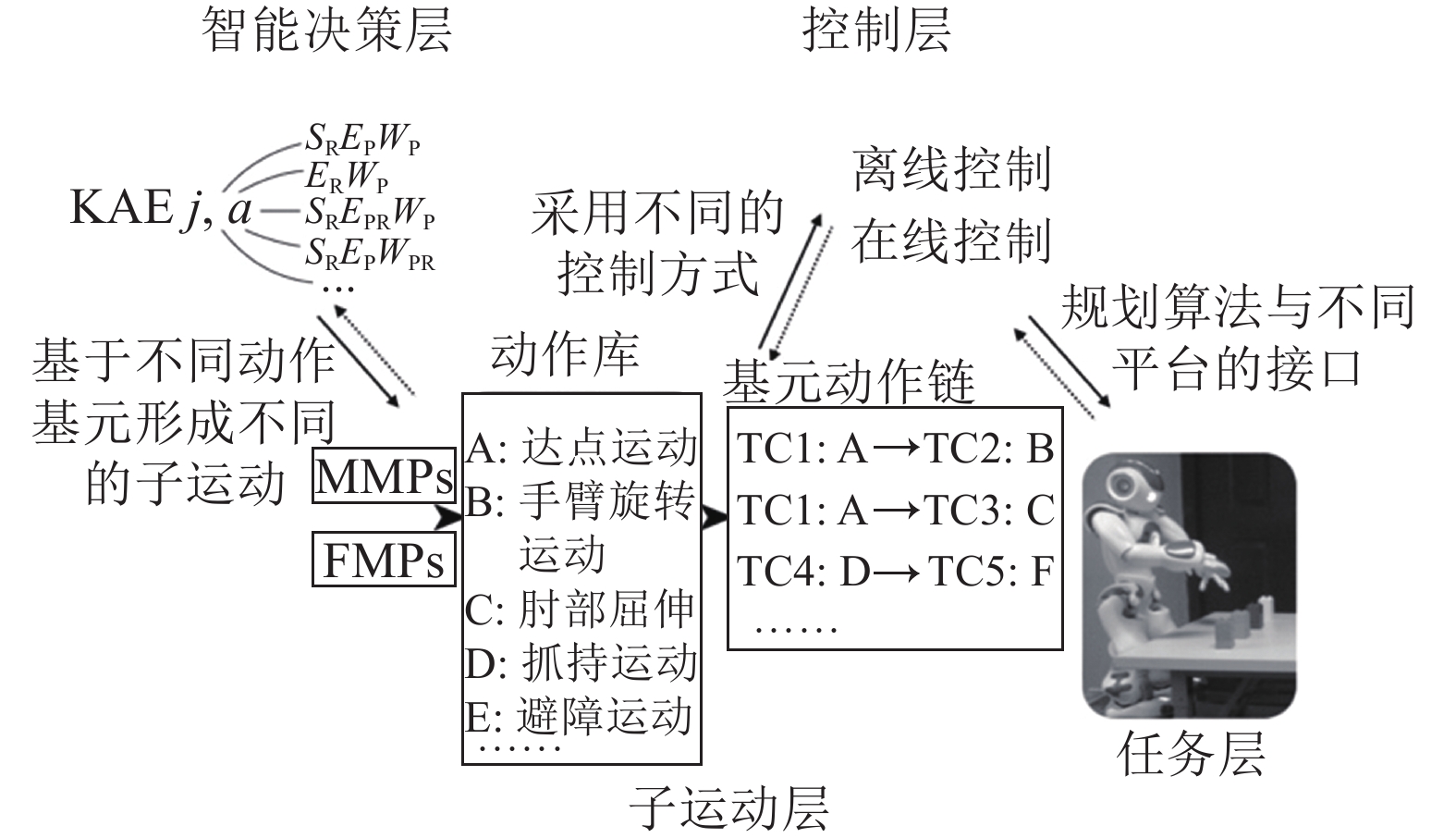 |
| 图4 拟人臂仿人运动框架 Fig. 4 Motion framework for anthropomorphic arms |
3 综合性逆运动学求解方法
根据动作基元的运动特点及NAO手臂结构,逆运动学问题可以通过两种方法解决:基于几何约束的反解算法和基于指标的反解算法。前者可通过特殊的几何结构获取解析解,对于不易获得解析解的动作基元采用后者。本文重点介绍基于指标的反解算法。
3.1 基于指标的反解算法对于其他动作基元,很难获取解析解。本文利用梯度投影法(gradient projection method,GPM)解决该类基元的逆运动学问题[18]。GPM是一种基于广义逆的算法,该算法将逆运动学问题的解分解为最小范数解和齐次解两部分,具体的表达式如下:
| ${\boldsymbol{\dot \theta }} = {{\boldsymbol{J}}^ + }{\boldsymbol{\dot X}} + {\boldsymbol{k}}({\boldsymbol{I}} - {{\boldsymbol{J}}^ + }{\boldsymbol{J}})\nabla {\boldsymbol{H}}$ | (1) |
式中,
显然,求解的关键在于目标函数H的确定。对于动作基元SREPWP、SREPRWP、SREPWPR、SRWPR、ERWPR、SREPRWPR,根据其腕部姿态在运动过程中是否改变又可以分为两类,这两类的目标函数H也有所不同。
3.1.1 WP类动作基元逆运动学求解动作基元SREPWP、SREPRWP所描述的运动类似于达点运动。在日常生活中,达点运动是最常见的运动,学者们对此进行了大量的研究。本文利用最小势能指标[4](minimum total potential energy,TPE)作为该类动作基元的臂姿预测指标。TPE由重力势能(gravitational potential energy,GPE)和弹性势能(elastic potential energy,EPE)两部分组成,势能f可定义如下:
| ${f_{{\rm{TPE}}}} = {f_{{\rm{GPE}}}} + {f_{{\rm{EPE}}}}$ | (2) |
GPE可通过式(3)求解得到:
| ${f_{{\rm{GPE}}}} = {m_{\rm{u}}}g{h_{\rm{u}}} + {m_{\rm{l}}}g{h_{\rm{l}}}$ | (3) |
式中,mu、ml分别为大臂与小臂的质量,hu、hl分别为大臂与小臂质心的高度。
用一种变系数的虚拟扭簧模型计算EPE:
| ${f_{{\rm{EPE}}}} = \mu {(\text{π} - \varphi )^2}/2$ | (4) |
式中,
因此,WP类动作基元的目标函数为:
| $\quad\quad\quad\quad\quad{H_R} = {m_{\rm{u}}}g{h_{\rm{u}}} + {m_{\rm{l}}}g{h_{\rm{l}}} + \mu {(\text{π} - \varphi )^2}/2$ | (5) |
不同于动作基元SREPWP、SREPRWP,基元SREPWPR、SRWPR、ERWPR、SREPRWPR所代表的运动模型在运动过程中需要考虑腕部的变化。因此,在应用TPE的基础上,需要考虑不舒适度所带来的影响。具体表达如下:
| $\begin{aligned}[b] {f_{{\rm{NTPE}}}} =& {f_{{\rm{TPE}}}} + \omega {f_{{\rm{wd}}}}= \\ & {m_{\rm{u}}}g{h_{\rm{u}}} + {m_{\rm{l}}}g{h_{\rm{l}}} + \mu {(\text{π} - \varphi )^2}/2 + \omega {({\theta _{{\rm{wa}}}} - {\theta _{{\rm{N}},{\rm{wa}}}})^2} \\ \end{aligned} $ | (6) |
式中:ω为不舒适度指标的权重系数,
同时,WR类基元所表达的运动形式与抓持运动相似。在生物物理学研究中,达点运动由大臂主导,而在抓取运动中,则是小臂起到主导作用。此时,小臂进行了大量的运动,而大臂受到小臂牵引靠着惯性进行随动,其运动距离相对较短,这也意味着肘关节运动的距离较短。因此本文提出最小肘部位移指标以完善WR类基元的优化指标。最小肘部位移表示如下:
| $\quad\quad\quad\min s = \sqrt {{{({x_{\rm{t}}} - {x_0})}^2} + {{({{{y}}_{\rm{t}}} - {y_0})}^2} + {{({{{y}}_{\rm{t}}} - {y_0})}^2}} $ | (7) |
式中,(x0,y0,
| ${\quad\quad{H_G}} = {k_{\rm{1}}}s(d - \Delta d)/d + {k_{\rm{2}}}{f_{{\rm{NTPE}}}}({q_{j = 1,2,3,4,5}})\Delta d/d$ | (8) |
式中:k1和k2为权重系数;d为当WP类基元转换为WR类基元时末端位置与目标位置的距离,当运动过程确定时,该距离为定值;∆d为运动过程中末端位置与目标位置的实时距离,该距离为变量;(d–∆d)/d和∆d/d为过渡项。权重系数共同保证了不同动作基元之间的平稳过渡,防止运动过程中关节的突变。
3.2 基于几何约束的反解算法当NAO采用一些动作基元(如ERWP和SRWP)完成任务时,并不是所有关节都激活并参与到运动中。同时,运动过程中腕部的姿态并没有发生改变。因此,当采用这类动作基元时,可以忽略腕部的运动。详细的运动信息如表3所示。
| 表3 ERWP和SRWP的运动形式 Tab. 3 Motion information of the ERWP and SRWP |
 |
如图5所示,本文引入了人臂三角形的概念描述手臂的构型,即由大臂和小臂组成的三角形[19]。在三角形中,可通过几何关系快速准确地求得待求关节角,具体的推导过程不赘述。
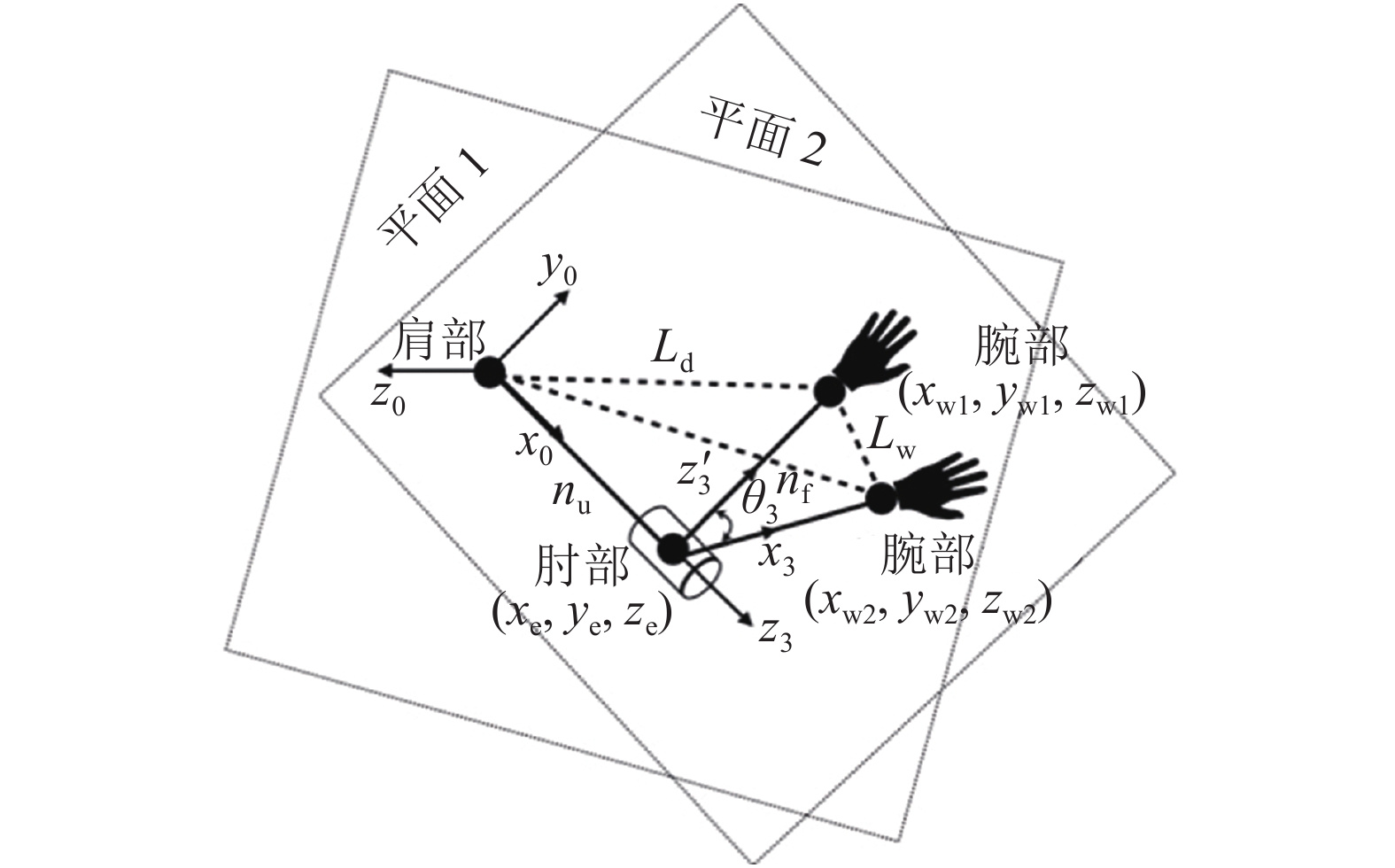 |
| 图5 NAO平台人臂三角形 Fig. 5 Arm triangle of the NAO |
4 实验仿真
分别进行了相似性实验和仿人运动实验两组实验验证。在相似性实验中,通过对不同实验者手臂运动的预测及对比,验证所提方法的准确性,并对精度进行验证。在仿人运动实验中,通过在NAO平台上进行的一组仿人运动实验,验证方法的可行性。
4.1 相似性实验验证一共有20名实验者参与到实验之中,每名实验者需要完成12组手臂运动实验,每组实验完成5次(20×12×5)。如图6所示,这12个点在同一竖直面上按照3行4列的形式均匀分布,每两点之间间隔为10 cm。实验者按要求以手臂自然下垂作为初始位姿开始运动,运动数据通过运动捕捉系统(natural point inc.)获取并作为比较数据。通过运动捕捉系统将采集到的人体运动数据将转换为NAO配置下的运动数据,这样既可以避免不同个体人臂臂长的差异性影响,也可以实现实验结果数据的统一表达。等比例缩放方法用将实际人臂臂姿转化为 NAO 的臂姿[7]。
 |
| 图6 相似性实验 Fig. 6 Similarity experiment |
表4统计实验者实验过程中的运动信息,每一个实验点需要20名实验者共计完成100次实验。表4时间为所有实验者在完成该点实验时所耗费的平均时间,实验者初始手部位置和目标点位置之间的距离越长,平均时间越长;动作基元表示运动过程中基元发生的先后顺序。从表4中可以看出,每名实验者在达到同一点时采用的动作基元是相同的,但不同实验点采用的动作基元却不相同,这进一步说明了人臂运动具有相似性和多样性的特点。在实验过程中发现,当实验者手臂初始位置与目标位置的距离较大时,往往采用较多的动作基元完成整个运动,同时动作基元发生的先后次序也较为固定。对于大多数的实验点,实验者往往采用基元SREPWP作为起始运动,验证了达点运动是人臂日常运动中最为常见的运动形式。但是,当实验者手臂初始姿态与实验点目标姿态存在某种特殊关系(如点P11和P12)时,会采取其他动作基元作为起始运动,此时距离并不是决定基元发生的首要因素。
| 表4 相似性实验运动数据 Tab. 4 Motion information of the similarity experiment |
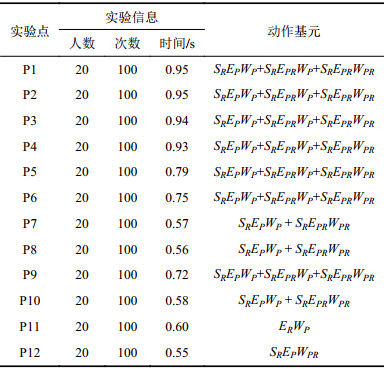 |
在实验过程中,通过运动捕捉系统及数据转换算法将实验者的末端轨迹及肘部位置可以转换为满足NAO手臂构型的运动数据。NAO采用同样的动作基元模拟每一名实验者在每一实验点的运动过程,其关节角通过本文所提反解算法进行求解。最终,将NAO在运动过程中的肘部位置与实际实验者的肘部位置进行比较,验证本文所提方法的有效性。图7为所有实验者在不同点处的误差分布。x、y轴分别表示列和行,其交叉点对应了12个实验点;z轴为NAO肘部位置与实验者实际肘部位置的距离误差。图7中每个交叉点附近的块表示不同实验者在该点处与NAO肘部位置的误差。从图7中可以看出,整体误差在1 cm以下,能够满足仿人运动的精度要求。同时,当整个运动包含动作基元的种类较多时,误差会越大。包含3种类型动作基元的实验点的误差(平均值0.7671 cm,标准偏差0.1132 cm)大于包含2种类型动作基元的实验点误差(平均值0.6421 cm,标准偏差0.0812 cm),而仅包含1种动作基元的实验点的误差是最小的(平均值0.21 cm,标准偏差0.1231 cm)。造成这种情况的原因在于运动捕捉系统的误差和实验者运动时存在的不确定性,导致无法准确地预测出运动过程中从一种基元转变为另一种基元时的精确位置;当运动过程中基元种类越多时,运动状态转换的次数也越多,相应的累积误差也越大。实验点P11处,反解算法采用的是基于几何约束的反解方法,可以得到解析解,但是由于运动捕捉系统的系统误差导致该点处仍然存在较小的误差。
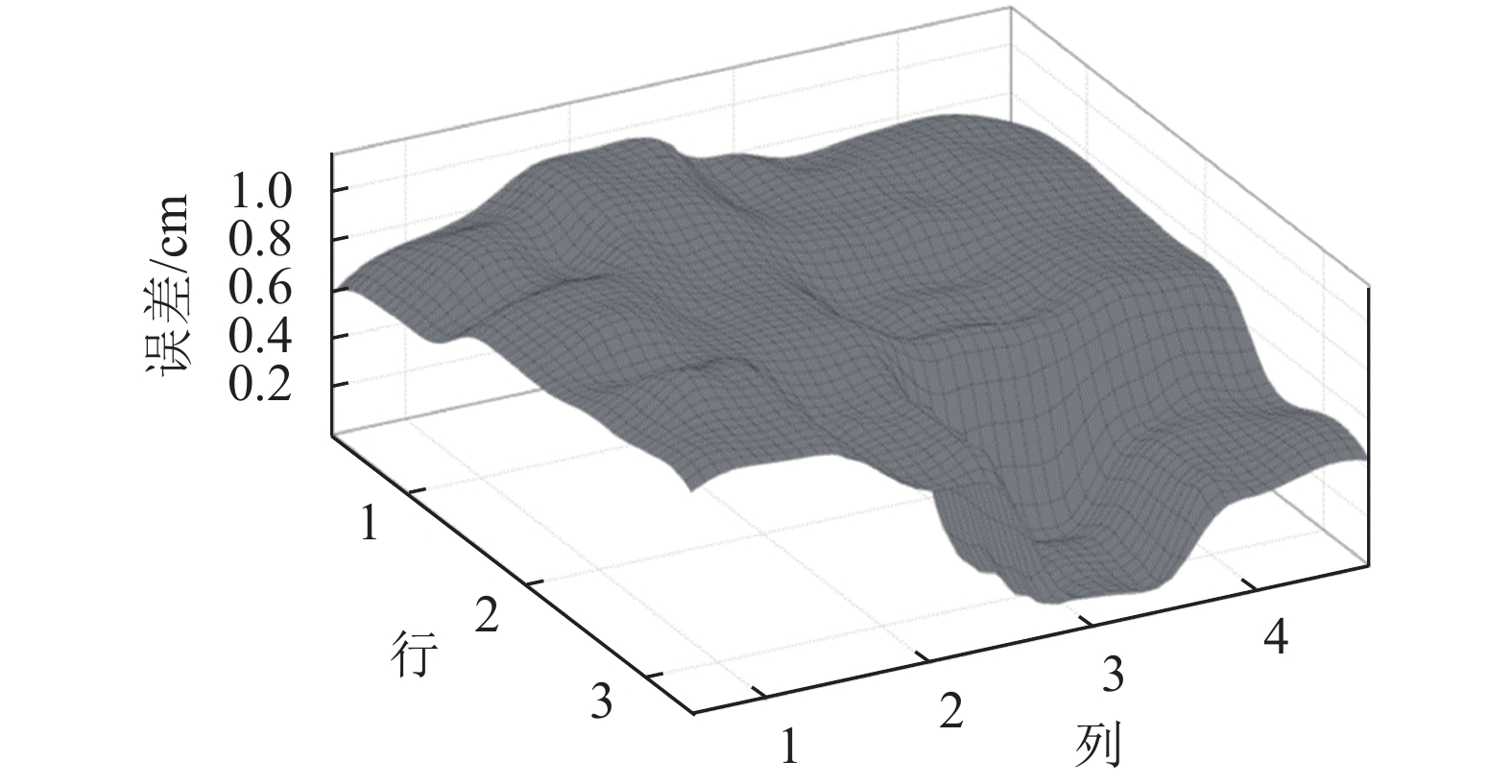 |
| 图7 不同实验点的肘部误差分布 Fig. 7 Elbow error distribution of all the points |
图8为每一名实验者在所有点处的平均误差及方差。图8中,横坐标表示20名实验者,纵坐标表示不同实验者的平均肘部误差值。20名实验者的标准偏差为0.0227 cm,说明该方法能够准确地模拟运动过程中不同实验者的手臂姿态,从而保证了仿人运动的精度。
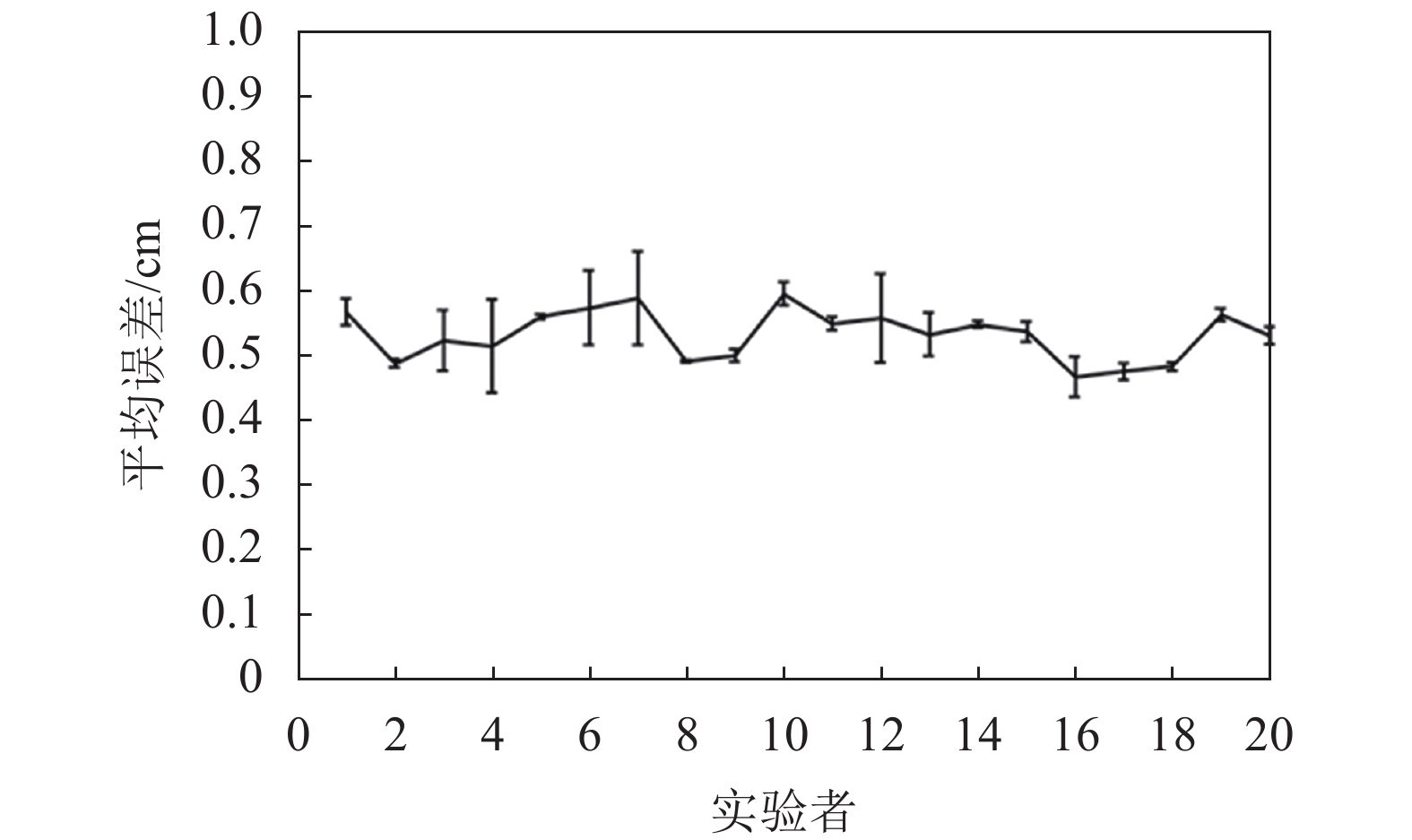 |
| 图8 不同实验者在所有实验点处的肘部误差分布 Fig. 8 Elbow error distribution of all the subjects |
4.2 仿人运动实验验证
利用本文所提方法在NAO机器人平台上进行了一组仿人运动实验,实验内容为NAO机器人自主地产生类人化的打招呼动作。图9为NAO机器人手臂运动过程。
 |
| 图9 仿人运动实验过程 Fig. 9 Process of human-like movement experiment |
实验开始前,10名实验者完成相同的运动,其手臂运动数据通过运动捕捉系统进行采集。运动过程中的部分手臂关键臂姿作为NAO机器人的目标臂姿。运动捕捉系统将采集到的运动数据同样进行标准化处理并转换为符合NAO手臂构型的运动数据。
将采用本文算法得到的臂姿与分别采用最小势能法和最小二乘法产生的臂姿进行了比较。相似性指标用于计算预测臂姿与实际臂姿的相似度,其表达式如下:
| $S(R,H) = \frac{1}{{1 + dist(R,H)}}$ | (9) |
式中:R、H分别表示预测得到的机械臂臂姿和实际人臂臂姿;S(R,H)表示相似度,其值域在(0,1]之间,数值越大,两者相似度越高;dist(R,H)表示机械臂臂姿及人臂臂姿在N维空间中的距离,对于NAO机器人,其手臂关节具有5个自由度,因此N为5。dist(R,H)可由式(10)计算得到:
| ${\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;dist({\theta _R},{\theta _H})} = {\left({\sum\limits_{i = 1}^N {\left\| {\frac{{{\theta _{R_i}} - {\theta _{H_i}}}}{{{\theta _{H_i\_\max }} - {\theta _{H_i\_\min }}}}} \right\|} ^2}\right)^{\frac{1}{2}}}$ | (10) |
式中,
3种不同算法的相似度值如图10所示,横坐标表示运动帧数,纵坐标表示相似度值。图10中,曲线的数值越大,预测的臂姿越接近真实臂姿。
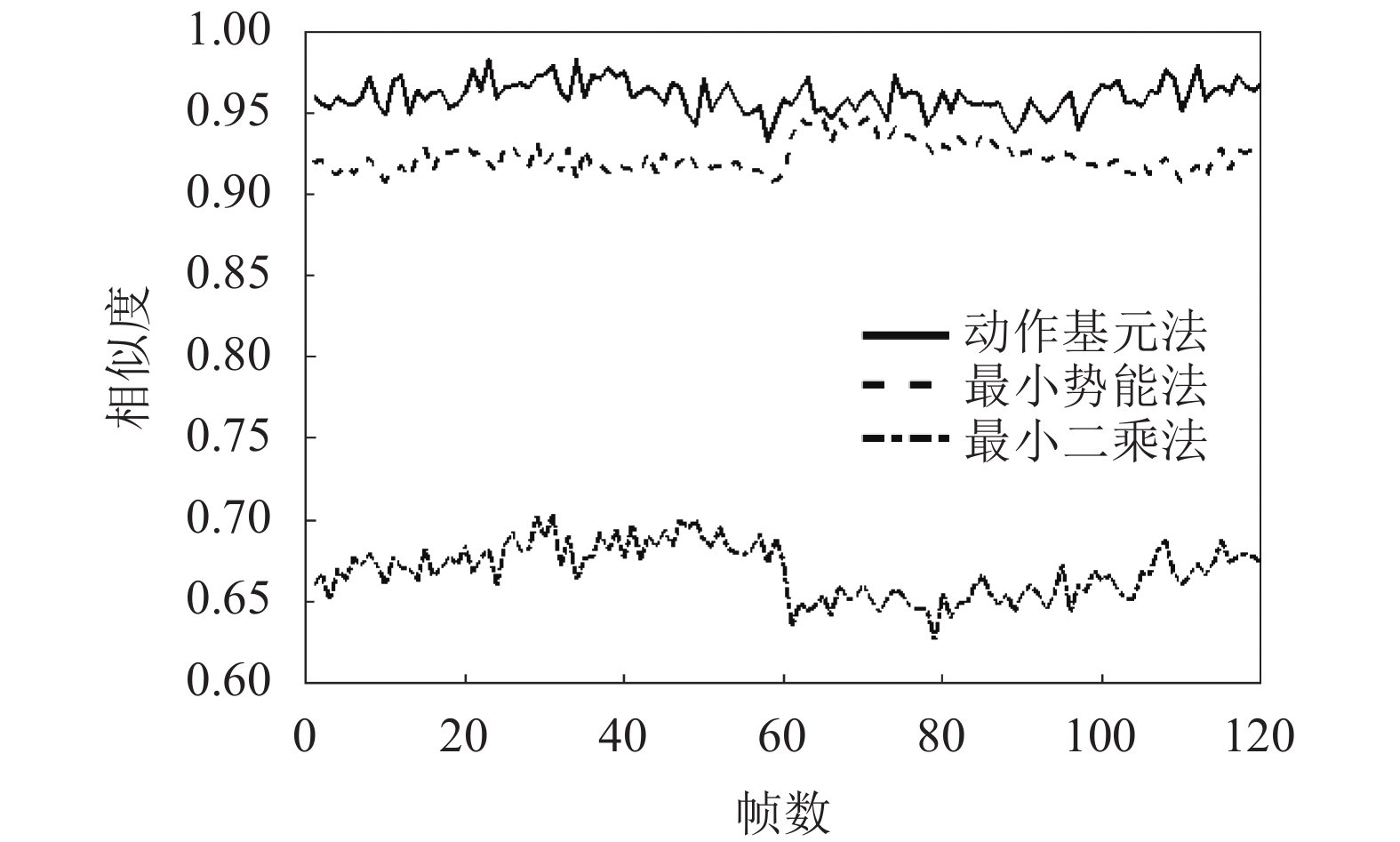 |
| 图10 3种算法的相似度曲线 Fig. 10 Similarity curves of three algorithms |
由图10可知:与最小二乘法相比,本文所提的动作基元法及最小势能法在仿人运动规划上有明显的优势。同时,动作基元法和最小势能法由于在某些阶段(帧数为60~80),采用的运动模型较为相似,则在这些阶段两种方法的相似度值较为接近。但是在整个运动过程中,最小势能法所得的相似度值(平均值0.9131,标准偏差0.0091)要小于动作基元法的相似度值(平均值0.9611,标准偏差0.0094)。这是因为最小势能法将运动中的手臂模型视为单一模型,在运动过程中并不会发生改变,忽视了人臂运动多样性的特点,因此无法保证全局的准确性。通过上述对比,说明本文所提方法在处理仿人运动多模型的问题上具有很好的优势,能够满足仿人运动的要求。
5 结 论提出了一种基于动作基元的规划方法实现拟人机械臂的仿人运动。基于动作基元的人臂运动表达方法不仅具有清晰的物理意义,能够反映出人臂运动的内在规律,而且模块化的建模思想将复杂的运动集合离散为多个、简单的运动子集。既能够保证较高的仿人运动精度,也为拟人臂仿人运动规划算法提供了便利。同时,该表达方法并不依赖于自由度数,只要目标平台具有明确的生理关节即可适用。最后,分别建立不同模型下的臂姿预测指标,并在NAO机器人平台上验证了方法的有效性。
基于动作基元的人臂运动表达是一种泛化的表达人臂运动的方式。通过对人臂生理关节的属性分析,确立了人臂运动的种类。但是在这些类别中,根据拟人臂机械关节的不同运动方式及环境约束,同一基元依然有不同的运动方式。动作基元的提出实际上是实现手臂模型的解耦,在下一阶段的研究中,将重点实现运动过程的解耦,从手臂模型和运动过程两方面共同完成手臂运动的解耦,从而进一步提高拟人臂仿人运动的精度。
| [1] |
Wang Mei,Lu Xichang,Tu Dawei,et al. Humanoid motion of manipulator that based on human-posture recognition[J]. Journal of Mechanical Engineering, 2016, 52(21): 26-34. [王梅,卢熙昌,屠大维,等. 基于人体动作姿态识别的机器人仿人运动[J]. 机械工程学报, 2016, 52(21): 26-34. DOI:10.3901/JME.2016.21.026] |
| [2] |
Yu Xiuli,Wei Shimin,Liao Qizheng. Development and technology research of humanoid robot[J]. Chinese Journal of Mechanical Engineering, 2009, 45(3): 70-75. [于秀丽,魏世民,廖启征. 仿人机器人发展及技术探索[J]. 机械工程学报, 2009, 45(3): 70-75. DOI:10.3901/JME.2009.03.071] |
| [3] |
Jung E S,Kee D,Chung M K. Upper body reach posture prediction for ergonomic evaluation models[J]. International Journal of Industrial Ergonomics, 1995, 16(2): 95-107. DOI:10.1016/0169-8141(94)00088-K |
| [4] |
Zhao Jing,Xue Biyun,Song Chunyu. Generating human-like movements for robotic arms[J]. Mechanism and Machine Theory, 2014, 81: 107-128. DOI:10.1016/j.mechmachtheory.2014.06.015 |
| [5] |
Gan Yahui,Dai Xianzhong,Lu Zhiyuan. Human-like manipulation planning for articulated manipulator[J]. Control Theory & Applications, 2013, 30(5): 549-557. [甘亚辉,戴先中,陆志远. 关节型机器人的似人操作构型规划[J]. 控制理论与应用, 2013, 30(5): 549-557. DOI:10.7641/CTA.2013.21047] |
| [6] |
Chevtchenko S F,Vale R F,Macario V,et al. Multi-objective optimization for hand posture recognition[J]. Expert Systems with Application, 2018, 92: 170-181. DOI:10.1016/j.eswa.2017.09.046 |
| [7] |
Artemiadis P K,Katsiaris P T,Kyriakopoulos K J. A biomimetic approach to inverse kinematics for a redundant robot arm[J]. Autonomous Robots, 2010, 29(3/4): 293-308. DOI:10.1007/s10514-010-9196-x |
| [8] |
Fang Cheng,Ding Xilun. Anthropomorphic arm kinematics oriented to movement primitive of human arm triangle[J]. Robot, 2012, 34(3): 257-264. [方承,丁希仑. 面向人臂三角形动作基元的拟人臂运动学[J]. 机器人, 2012, 34(3): 257-264. DOI:10.3724/SP.J.1218.2012.00257] |
| [9] |
He Wei,Chen Yuhao,Yin Zhao. Adaptive neural network control of an uncertain robot with full-state constraints[J]. IEEE Transactions on Cybernetics, 2017, 46(3): 620-629. DOI:10.1109/TCYB.2015.2411285 |
| [10] |
Liu Weihui,Chen Diansheng,Steil J. Analytical inverse kinematics solver for anthropomorphic 7-DOF redundant manipulators with human-like configuration constraints[J]. Journal of Intelligent & Robotic Systems, 2017, 86(1): 63-79. DOI:10.1007/s10846-016-0449-6 |
| [11] |
Mrotek L A,Bengtson M,Stoeckmann U T,et al. The arm movement detection (AMD) test:A fast robotic test of proprioceptive acuity in the arm[J]. Journal of Neuroengineering & Rehabilitation, 2017, 14(1): 64. DOI:10.1186/s12984-017-0269-3 |
| [12] |
Wei Ye,Jia Danping. Research on robotic arm movement grasping system based on MYO[J]. Journal of Physics(Conference Series) 2021, 1754(1): 012173. DOI:10.1088/1742-6596/1754/1/012173 |
| [13] |
Zhao Jing,Wei Yuan. A novel algorithm of human-like motion planning for robotic arms[J]. International Journal of Humanoid Robotics, 2017, 14(1): 1-27. DOI:10.1142/S0219843616500237 |
| [14] |
Denavit J,Hartenberg R S. A kinematic notion for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1995, 22(2): 215-221. |
| [15] |
Tamar F,Binyamin H. Motor primitives in vertebrates and invertebrates[J]. Current Opinion in Neurobiology, 2005, 16(6): 660-666. DOI:10.1016/j.conb.2005.10.011 |
| [16] |
Okamoto T,Shiratori T,Kudoh S,et al. Toward a dancing robot with listening capability:Keypose-based integration of lower-,middle- and upper-body motions for varying music tempos[J]. IEEE Transactions on Robotics, 2014, 30(3): 771-778. DOI:10.1109/TRO.2014.2300212 |
| [17] |
Wei Yuan,Zhao Jing. Designing robot behavior in human robot interaction based on emotion expression[J]. Industrial Robot, 2016, 43(4): 380-389. DOI:10.1108/IR-08-2015-0164 |
| [18] |
Liegeois A. Automatic supervisory control of the configuration and behavior of multibody mechanisms[J]. IEEE Transactions on Systems,Man and Cybernetics, 1977, 7(12): 868-871. DOI:10.1109/tsmc.1977.4309644 |
| [19] |
Berman S,Liebermann D G,Flash T. Application of motor algebra to the analysis of human arm movements[J]. Robotica, 2008, 26(4): 435-451. DOI:10.1017/S0263574707003979 |
 2021, Vol. 53
2021, Vol. 53

