船舶舵机可以实现船舶航向控制和减摇功能，因转叶舵机具有体积小、成本低、兼容性强等优点，一经提出迅速成为研究的热点^[1-4]。但转叶舵机结构存在饱和非线性的缺陷，且有水动力负载干扰，舵叶转动呈现出明显的时滞、位置精度不高等问题。

针对上述问题，国内外学者尝试了诸多方法^[5-8]。通过设置控制器限制转舵角度、角速度使舵机工作在非饱和线性区，以牺牲操作区间保证系统的平稳性^[9]，来解决舵机的饱和非线性问题。对于转舵系统的时滞、位置精度不高，解决办法主要分为两大类。其一，是机械反馈控制的办法；其二，是控制器补偿的方法。例如：苏文海等^[10-11]基于蚁群算法和退火理论，提出一种具有不完全微分的PD控制器设计方法，基于反馈理论设计出一种带有负载力矩观测补偿器的鲁棒控制器，小角度操舵时，可有效抑制负载力矩等干扰；Liang^[12]、张宇^[13]、周柳明^[14]等根据首摇和横摇对舵的分频响应特性，基于控制理论设计首摇和横摇控制器，在相应的频带内具有指定的性能，系统鲁棒性满足要求；此外，刘志全等^[15]基于航速保持的思想设计舵减摇控制器，张文颖等^[16]基于模糊T–S模型提出模糊观测器设计方案，刘胜等^[17]设计了μ–鲁棒控制器用于舵减摇控制。总结已有研究，由于外负载多变且与舵机转角构成强力位耦合关系，这种方法不能从根源上彻底消除偏差，且补偿效果受限于结构，舵机性能仍有较大提升空间。

作者从转叶舵机结构出发，提出复式液压摆动缸操舵原理，既能抵消水动力负载的干扰，从根源上解决转叶舵机操控性问题，又可增大舵机的非饱和线性区间，提升船舶操纵效果。

舵机位置布置如图1所示。图1中，水动力在舵叶上的作用中心R(x_R，z_R)与船舶的重心O(x₀，z₀)既不在同一水平面上，也不在同一铅锤面上，操舵时，舵叶对水的作用力F绕z轴方向产生首摇力矩T_z(F)控制航向，绕x轴方向产生横摇力矩T_x(F)用于减摇。但水动力对舵叶的反作用力F′会产生跑舵现象，降低舵机系统的稳定性、快速性和转舵位置精度。

图1(Fig. 1)

图1 船舶受力模型 Fig. 1 Model of ship force model

以直驱式电液伺服转叶舵机为例，分析水动力对舵机系统的影响。直驱式电液伺服转叶舵机控制系统通常由计算机控制系统、调速机构、液压动力机构、角度传感器等部分组成，原理图如图2所示。

图2(Fig. 2)

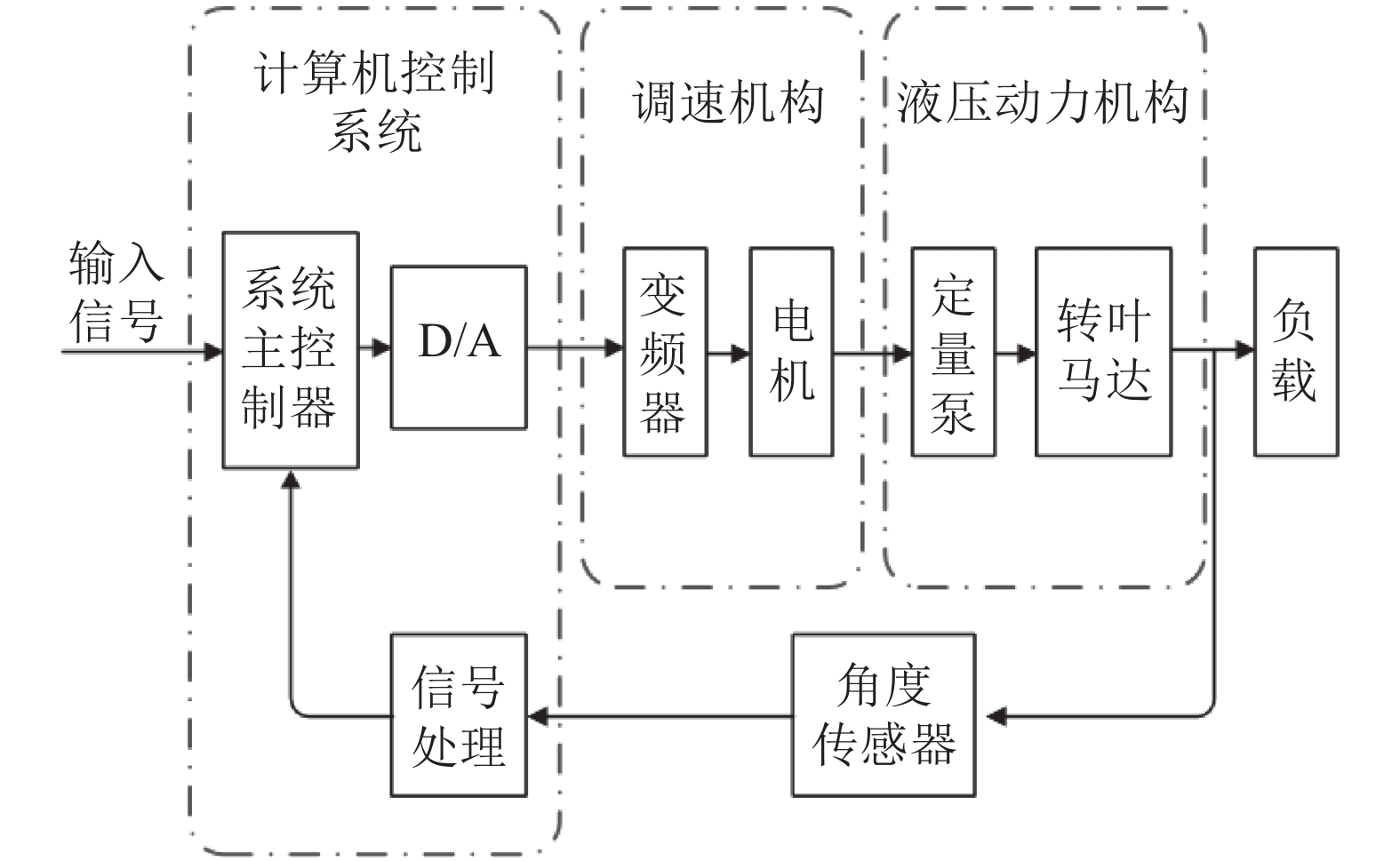图2 直驱式电液伺服转叶舵机原理图 Fig. 2 Principle diagram of direct-drive electro-hydraulic servo rotary steering gear

调速机构由变频器和变频电机组成，计算机控制系统输出控制电压u_c到变频器，变频器输出控制电机转动的相电压U_m，进而电机输出负载转矩T_LT，带动定量泵工作。该环节中，变频器函数表达式为：

式中：K_f为频率转电压系数，V/Hz；K_V为电压转频率系数，Hz/V。

电机和负载的力矩平衡方程为：

式中：J_T为电机轴上的转动惯量，kg·m²；B_T为电机阻尼系数，N·m/(rad·s^–1)；ω_p为电机转子角速度，rad/s；θ_p为电机转子角位移量，rad；K_T为转轴弹性转矩系数，这里可忽略；T_E为电磁转矩，N·m。 ${T_{\rm{E}}} = {K_{{\rm{E1}}}}{U_{\rm{m}}} - {K_{{\rm{E2}}}}{\omega _{\rm{p}}} $ ， ${T_{{\rm{LT}}}} = {D_{\rm{p}}}({p_{\rm{o}}} - {p_{\rm{i}}})/{\eta _{{\rm{pm}}}} $ 。其中：K_E1、K_E2为电机定常系数；D_p为定量泵的排量，m³/rad；P_o为泵的出口压力，Pa；P_i为泵的入口压力，Pa；η_pm为定量泵的机械效率，取0.9。

液压动力机构为泵控马达模型，在进行液压系统理想化假设的基础上，液压马达转角与任意负载力矩的函数关系，由流量连续性方程和力矩平衡方程给出：

式中：D_m为定量马达的排量，m³/rad；η_pv定量泵的容积效率；θ_m为马达实际角位移，rad；V_o为单一腔室的等效容积，m³；β_e为有效体积弹性模量，Pa；C_t为总泄漏系数，(m³/s)/Pa；J_m为马达轴上的转动惯量，kg·m²；B_m为马达阻尼系数，N·m/(rad/s)； ${T_{\rm{L}}}({\theta _{\rm{m}}})$ 为水动力负载力矩，N·m。

舵机负载主要为水动力负载^[18-20]，为近似描述舵叶上的水动力负载，假设在来流速度为v且冲角为θ_m的均匀流场中，舵叶所受水动力为F_R，作用点到舵轴的距离为d，如图3所示。F_R可分解为沿来流方向的阻力F_D和垂直于来流方向的升力F_L，也可分解为垂直于舵叶轴面的正压力F_N和沿舵叶轴面的切向力F_T。水动力作用于舵轴的扭矩可表示为：

图3(Fig. 3)

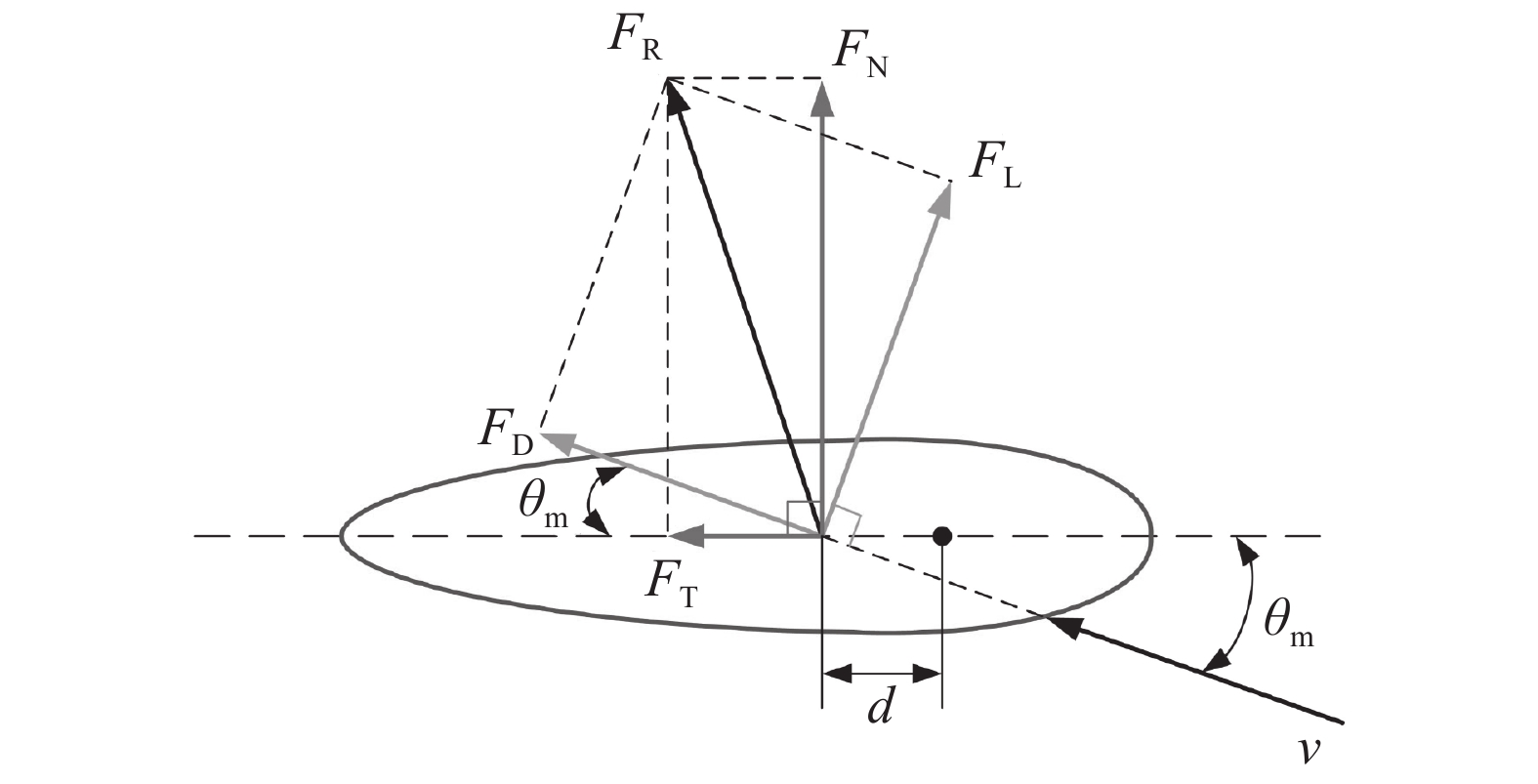图3 舵叶表面受力示意图 Fig. 3 Force diagram of rudder blade surface

式中：C_L为舵升力系数，C_D为阻力系数，无量纲；ρ为海水密度，kg/m³； $A $ 为舵叶单侧浸水面积，m²。

角位移传感器，其传递函数为：

式中：U_c为位移传感器输出电压，V；K_b为角度传感器增益，V/rad。

联立方程（1）～（6）可得直驱式电液伺服转叶舵机的方框图，如图4所示。

图4(Fig. 4)

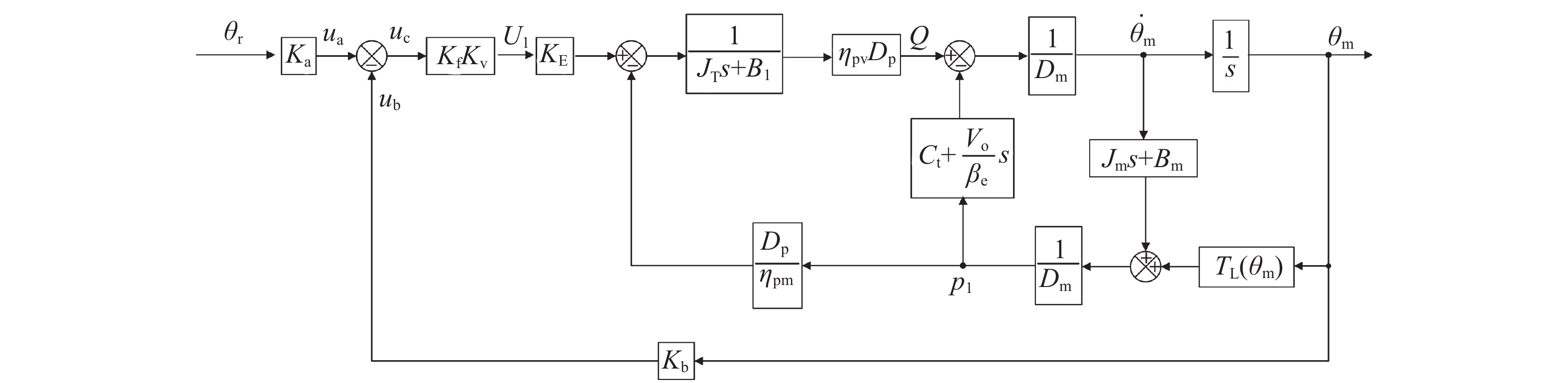图4 转叶舵机数学模型 Fig. 4 Mathematical model of rotary steering gear

由图4数学模型可知，舵叶上作用的水动力产生的干扰力矩与舵机角位移的关系可表示为：

于是，舵角偏差e可表示为：

式中：

从式（8）可知，该直驱式转叶舵机为4阶系统，舵角与水动力负载力矩T_L构成强力位耦合关系。舵机转动时，水动力负载变化，负载变化又使得舵角产生偏差，且偏差值波动范围较大，这一结论可通过实验台上的实测数据得以验证^[21]。

如图5所示，复式摆动缸由舵驱动缸转子1、力矩解耦缸转子2、壳体3，定叶片4、5和动叶片6、7等组成。驱动缸转子与解耦缸转子之间形成内密闭容腔，解耦缸转子与壳体之间形成外密闭容腔，内外层转子上均开设环形油道，内密闭容腔采用轴配流的方式配流，外密闭容腔采用壳体配流的方式配流。当高压油液进入内密闭容腔，驱动缸转子在液压力F作用下顺时针转动，此时舵叶在与驱动缸转子固连的舵杆的带动下顺时针旋转一角度θ。在舵叶转动过程中必然存在反方向水动力F′的干扰，使容腔Ⅰ体积减小∆V，到达新的平衡位置，单层摆动缸转子将回旋，造成跑舵。而复式摆动缸为确保驱动缸转子不动，可通过顺时针旋转解耦缸转子（驱动缸定子），使容腔Ⅰ体积减小∆V，达到平衡状态。即相当于解耦缸与水动力在舵驱动缸转子上产生大小相等方向相反的力矩，合力矩为零达到解耦目的。在合外力矩为零时，舵驱动缸低速启动性能得到极大提升，系统时滞降到最小。此外，在复式摆动缸解耦过程中，由于内外层转子同向旋转，内层转子与外层转子的相对工作区间不变，但内层转子的绝对非饱和线性区间是增大的，即舵叶有更大的转角范围（此原理类似于多级液压缸），以备紧急转向。

图5(Fig. 5)

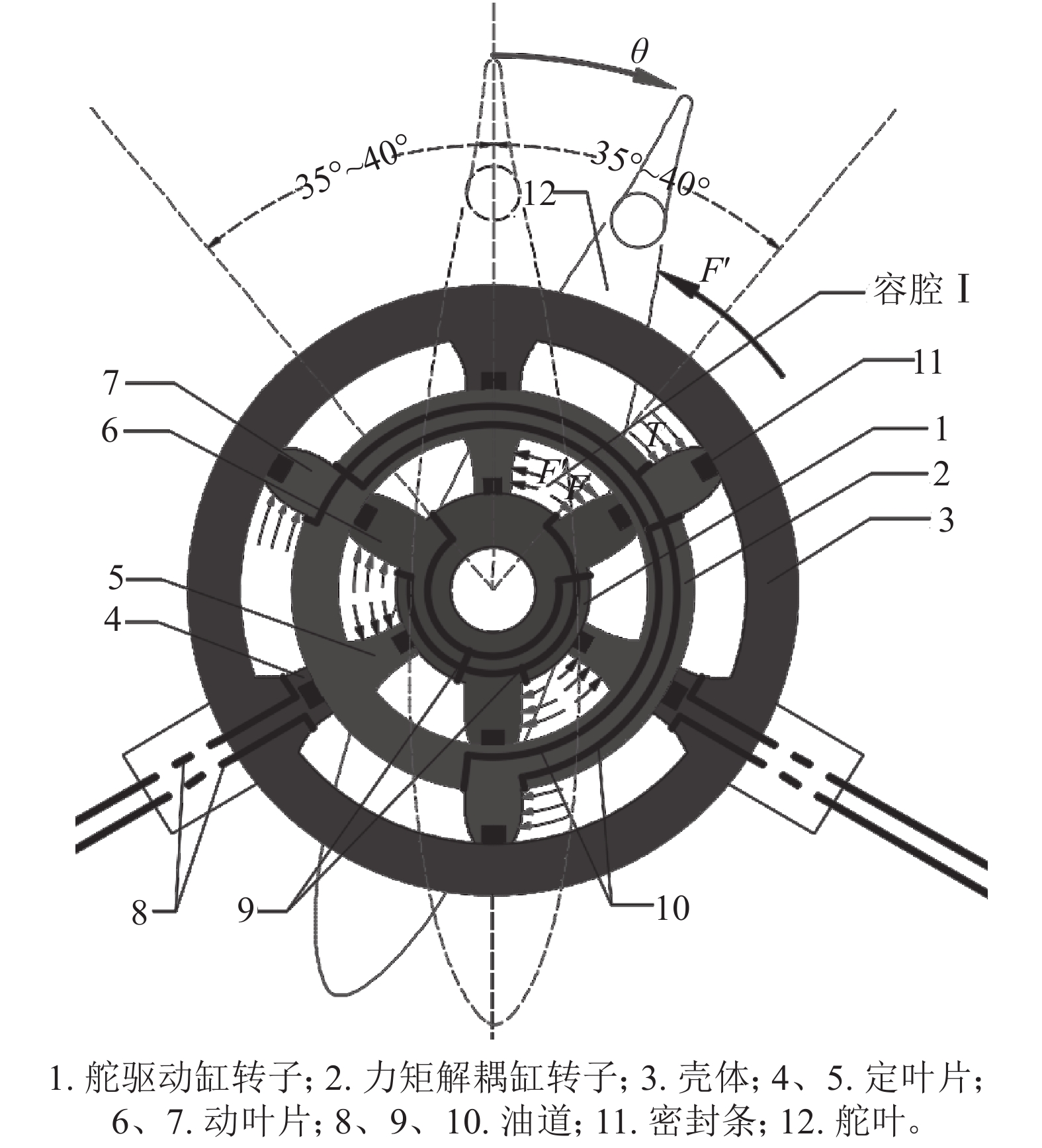图5 复式摆动缸工作原理图 Fig. 5 Operational principle diagram of compound swing cylinder

由复式摆动缸工作原理可知，驱动缸转子进行位置控制，解耦缸转子进行力矩控制，由于实船操舵过程中所受水动力负载较大，不易直接测量，可设计力矩解耦控制器，通过式（5）得到近似值，观测得到的力矩值经转换作为解耦缸转子的力矩控制信号，采用前馈控制确保作用于舵驱动缸转轴上的合力矩为零。复式摆动缸用于舵机系统解耦方框图如图6所示。

图6(Fig. 6)

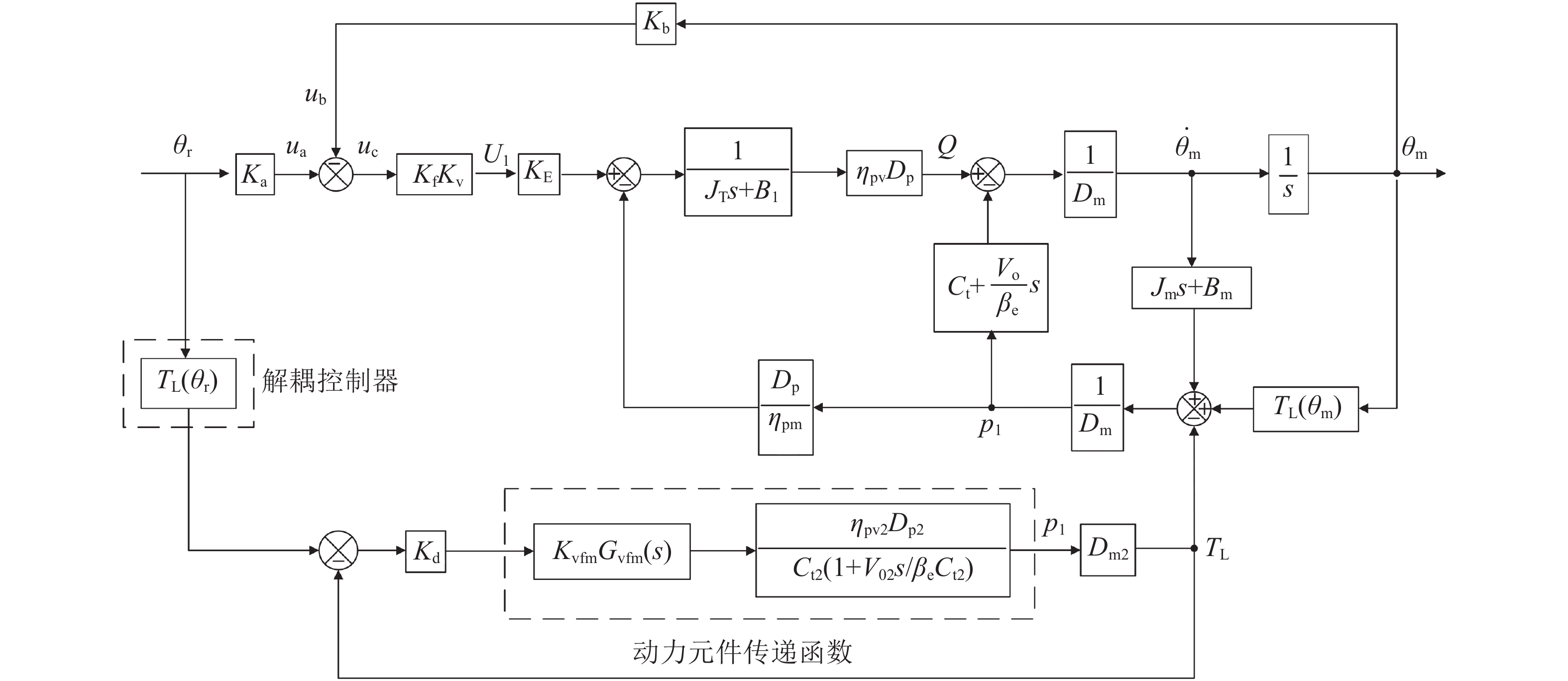图6 复式摆动缸解耦方框图 Fig. 6 Decoupling block diagram of compound swing cylinder

消除实时变化的外负载力矩，直驱式舵机系统的动态性能主要取决于变频电机和液压动力机构，由于在本实验中采用的变频电机频宽远高于液压动力机构频宽，在不影响直驱式舵机系统整体性能分析的情况下，可将机电调速模型简化为1阶惯性环节，则该系统的开环传递函数为：

式中：K为开环增益， $K{\rm{ = }}\dfrac{{{K_{\rm{a}}}{K_{\rm{f}}}{K_{\rm{v}}}{K_{\rm{E}}}{\eta _{{\rm{pv}}}}{D_{\rm{p}}}}}{{{D_{\rm{m}}}}}$ ；T_d为电机的时间常数；ω_h为系统固有频率， ${\omega _{\rm{h}}} = \sqrt {\dfrac{{{\beta _{\rm{e}}}D_{\rm{m}}^2}}{{{J_{\rm{m}}}{V_{\rm{t}}}}}} $ ； ${\zeta _{\rm{h}}}$ 为系统阻尼比， ${\zeta _{\rm{h}}}{\rm{ = }}\dfrac{{{C_{\rm{t}}}}}{{2{D_{\rm{m}}}}}\sqrt {\dfrac{{{\beta _{\rm{e}}}{J_{\rm{m}}}}}{{{V_{\rm{t}}}}}} + \dfrac{{{B_{\rm{m}}}}}{{2{D_{\rm{m}}}}}\sqrt {\dfrac{{{V_{\rm{t}}}}}{{{\beta _{\rm{e}}}{J_{\rm{m}}}}}} $ 。

根据直驱式舵机系统各元器件参数和复式摆动缸结构参数，可得系统主要参数，如表1所示。

表1(Tab. 1)

表1 舵机系统参数 Tab. 1 System parameters of steering gear

表1 舵机系统参数 Tab. 1 System parameters of steering gear 参数名 数值 驱动缸叶片内径d11/mm 650 驱动缸叶片外径d12/mm 1050 驱动缸转动惯量Jm/(kg·m2) 600 驱动缸阻尼系数Bm/(N·m·s·rad–1) 0.05 解耦缸叶片内径d21/mm 1190 解耦缸叶片外径d22/mm 1390 解耦缸转动惯量Jmm/(kg·m2) 600 解耦缸阻尼系数Bmm/(N·m·s·rad–1) 0.05 叶片宽度b/mm 650 驱动缸排量Dm/(m3·r–1) 0.354 解耦缸排量Dmm/(m3·r–1) 0.37 变频电机功率P/kW 51.85 变频电机时间常数Td/s 0.30 定量泵排量Dp/(mL·r–1) 68.42 液压腔总容积Vt/m3 0.45 油液体积弹性模量βe/Pa 6.9×108 总泄漏系数Ct/(m3·s–1 ·Pa–1) 4×10–7 扭矩传感器增益Kt/(V·N–1·m–1) 2.4×10–6 角位移传感器增益Kb/(V·rad–1) 16.38 电压转换频率系数Kv/(Hz·V–1) 10 频率转换电压系数Kf/(V·Hz–1) 3.8 电机定常系数KE 26.27 定量泵的容积效率ηpv 0.9

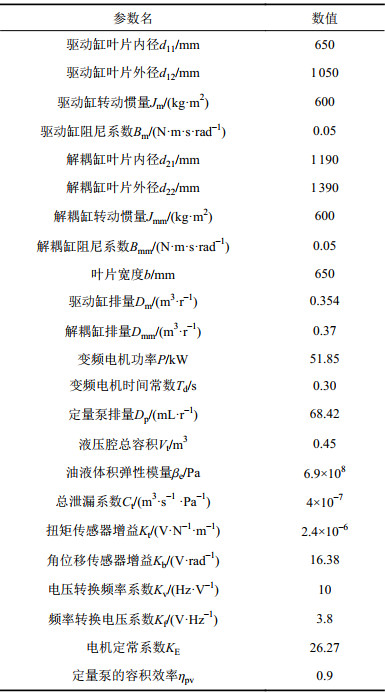从式（9）可知，该系统为Ⅰ型伺服系统，结合表1中主要参数，可画出复式摆动缸操舵系统开环伯德（Bode）图、奈奎斯特（Nyquist）图如图7所示。

图7(Fig. 7)

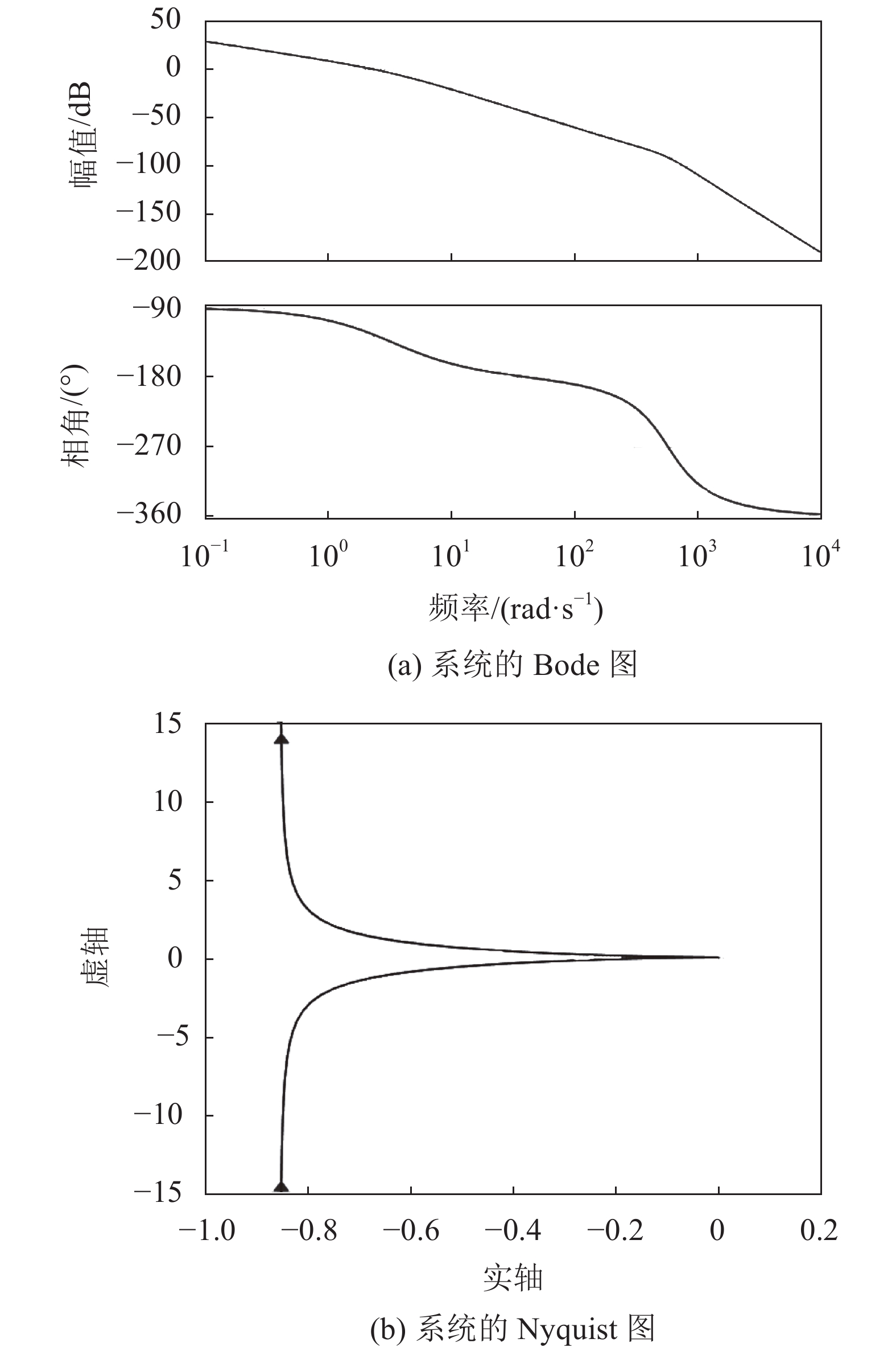图7 舵机系统开环稳定性分析 Fig. 7 Analysis of the open loop stability of steering gear system

由图7可知：该系统的幅值裕度为45.3 dB，相角裕度为54.9°，截止频率为2.32 rad/s，穿越频率为41.7 rad/s。系统右半平面无开环极点，奈奎斯特曲线远离点(–1，0)，由稳定性判据可知，系统稳定且具有较大的稳定裕量。

在保证机械部件刚度的前提下，系统闭环响应特性，只需考虑对指令信号的响应特性。由式（9）和表1可求得系统的闭环传递函数为：

根据式（10）可画出系统的闭环频率特性曲线，如图8所示。该曲线反映了伺服系统的响应能力，从图8中可以看出，系统幅值下降到0.707时，对应的频率为3.743 rad/s，相位滞后90°时对应的频率为3.062 rad/s。由于转叶舵机系统的开环阻尼比ζ_h较小，闭环振荡环节的固有频率较高，系统的响应速度主要取决于惯性环节，所以要提高系统的响应速度，必须保证惯性环节的频宽，同时提高液压系统固有频率并适当提高阻尼比。

图8(Fig. 8)

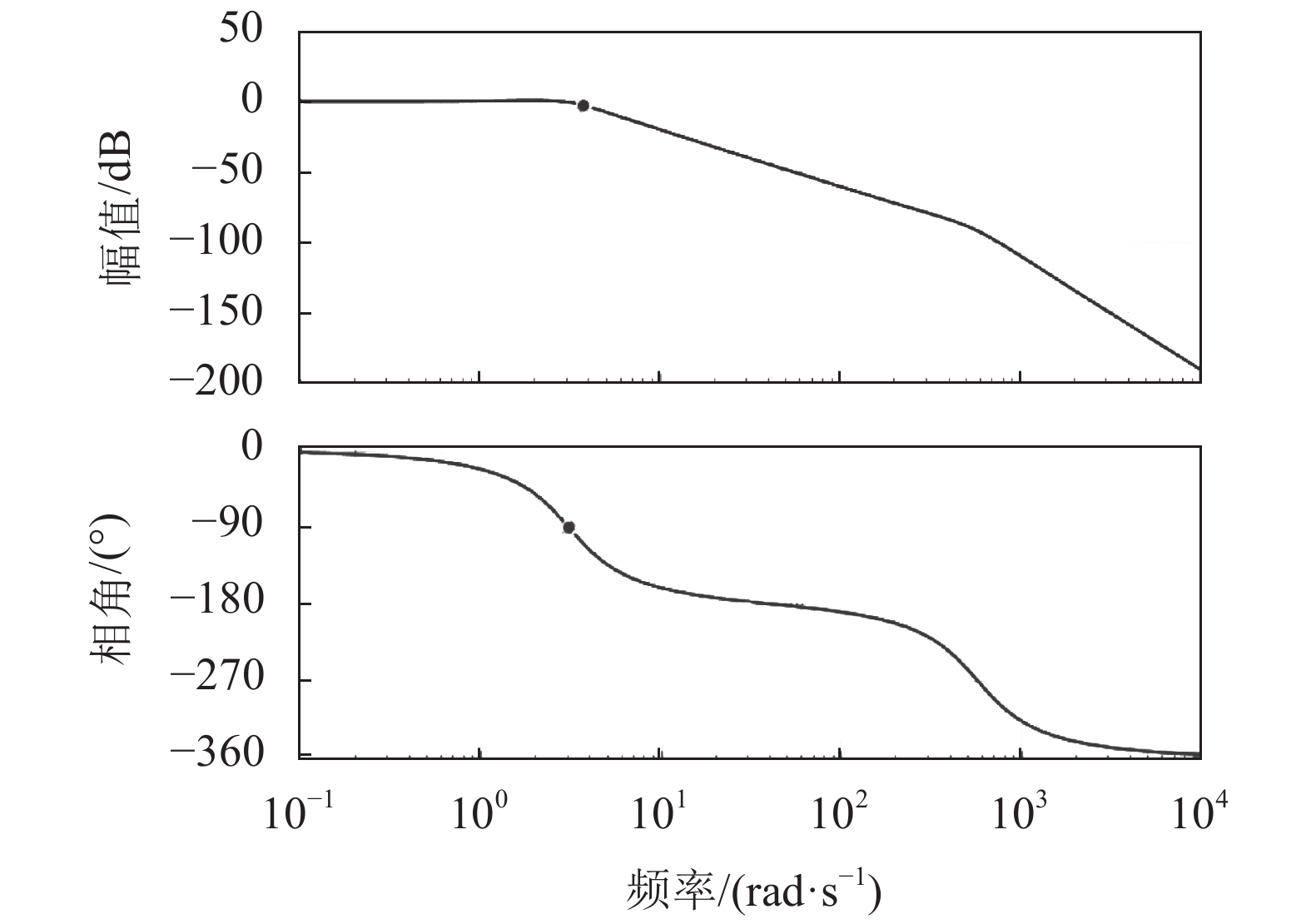图8 舵机系统闭环频率特性分析 Fig. 8 Analysis of closed-loop frequency characteristics of steering gear system

为验证复式液压摆动缸消除水动力干扰的有效性，搭建AMESim仿真模型，如图9所示。以船舶转叶舵机的实际工况为基础，在水动力干扰下，对舵机系统的低速跟踪性能进行仿真，并与传统PID控制器控制下的舵机系统性能相比较。

图9(Fig. 9)

图9 复式摆动缸的解耦AMESim仿真模型 Fig. 9 Decoupling AMESim simulation model of compound swing cylinder

图10（a）、（b）、（c）分别为转叶舵机跟踪幅值35°的阶跃信号、斜率0.01°/s的斜坡信号及幅值35°、频率0.032 Hz的正弦信号时的仿真曲线。曲线1表示信号线，曲线2表示采用传统PID控制器的仿真曲线，曲线3表示复式摆动缸控制下的仿真曲线，图10（b）中的曲线4表示位置误差带。

图10(Fig. 10)

图10 解耦仿真曲线 Fig. 10 Decoupling simulation curves

由图10（a）可知，复式摆动缸操控舵杆转角与传统PID控制器相比，响应速度更快，在7 s左右达到稳态，无超调，且稳态误差维持在±0.05°范围内，相较于传统摆动缸达到稳态的速度提升约36%。图10（b）为跟踪斜率为0.01°/s的斜坡信号时舵角的变化曲线。

从图10（b）中可知，复式摆动缸解耦后的舵机低速性能明显优于传统PID控制器控制下的舵机低速性能，转舵精度保持在±0.03°位置误差带内，满足设计要求。图10（c）的正弦响应曲线则表明随着时间的推移复式摆动缸控制舵角对指令信号的跟随性能几乎无变化，具有较好的频域鲁棒性。

1）通过对转叶舵机工作原理、数学模型的分析，阐明了操舵过程中水动力产生的负载力矩与舵角的力位耦合关系，及对船舶操控性能的影响。

2）针对转叶舵机结构的饱和非线性、外负载多变且与舵角的强力位耦合关系，提出复式摆动缸用于转叶舵机的新原理，从根本上解决了水动力对舵角的位置干扰。

3）仿真分析表明复式摆动缸用于转叶舵机可提高船舶操控性能的有效性，相比于传统控制器设计的方法，这种结构解耦的方法可靠性更高。