泥沙问题关系到水库功能的充分发挥,如何减缓水库泥沙淤积和控制淤积速度,保持水库的可持续利用,成为国内外共同关注的问题。三峡水库蓄水以来,库区水沙运动特性较蓄水前发生改变,坝前水位抬升导致库区流速降低,水流挟沙力降低,故库区泥沙发生淤积。因此研究三峡水库泥沙淤积对于三峡水库优化调度具有重大意义[1-2]。
水库泥沙淤积问题一直备受研究学者们的关注。由于河床冲淤的反馈作用总是滞后于不断变化的来水来沙条件及调度控制等扰动,反馈和滞后的作用需要足够的时间反映出来[3]。吴保生[4]基于河道的自动调整原理,发现水库泥沙冲淤过程具有溯源特点,在时间上表现水库泥沙淤积与水沙条件等因素之间存在着长时段的滞后响应关系,在此基础之上,建立了滞后响应模型,并将其运用在三门峡水库淤积[5-7]、平滩流量[8]以及平滩面积[9]研究中。滞后响应模型在使用过程中需要根据具体的河段演变特点进行调整优化。邵文伟[10]、郑珊[11-12]、吕宜卫[13]等根据黄河小北干流、三门峡水库和荆江河段等不同河段冲淤特点,对滞后响应模型进行相应的调整和优化。李凌云等[14-16]针对滞后响应模型中的不足,对模型中调整系数进行修正,提高了模型的计算精度。对于三峡水库而言,目前仅有唐小娅等[17]采用沙量加权平均坝前水位的方法建立了三峡水库泥沙淤积滞后响应模型,并初步探讨了汛期泥沙淤积滞后响应规律,但未考虑水库来流和泥沙粒径的影响。泥沙淤积滞后响应规律对于三峡水库泥沙淤积研究不可忽视,有必要深入开展针对三峡水库泥沙淤积滞后响应规律的研究。
本文在分析三峡水库汛期入库水沙特性、库区泥沙冲淤变化的基础上,参考以往水库滞后响应规律的相关研究,开展了以下工作:1)分析了金沙江下游梯级水库(以下简称梯级水库)蓄水前后三峡水库入库水沙条件以及库区泥沙淤积特性变化;2)通过考虑流量、含沙量、泥沙粒径以及坝前水位建立模拟精度更高的三峡水库泥沙淤积滞后响应模型;3)基于上述滞后响应模型,进一步分析不同影响因素对库区泥沙淤积的影响,揭示了梯级水库蓄水前后三峡水库泥沙淤积滞后响应规律,分析了梯级水库蓄水对三峡水库泥沙淤积的影响。
1 研究方法与数据来源 1.1 研究河段概况本次研究是以三峡水库为核心开展的,三峡水库坝址位于宜昌市三斗坪,水库正常蓄水位175 m,对应研究范围为坝址至上游660~760 km(江津—朱沱),干流自上而下沿程设有朱沱、寸滩、清溪场、万县、庙河5个水文站,图1为三峡水库库区示意图。向家坝、溪洛渡水电站分别于2012、2013年开始蓄水运行[18],标志着金沙江下游梯级水库群开始联合蓄水拦沙。
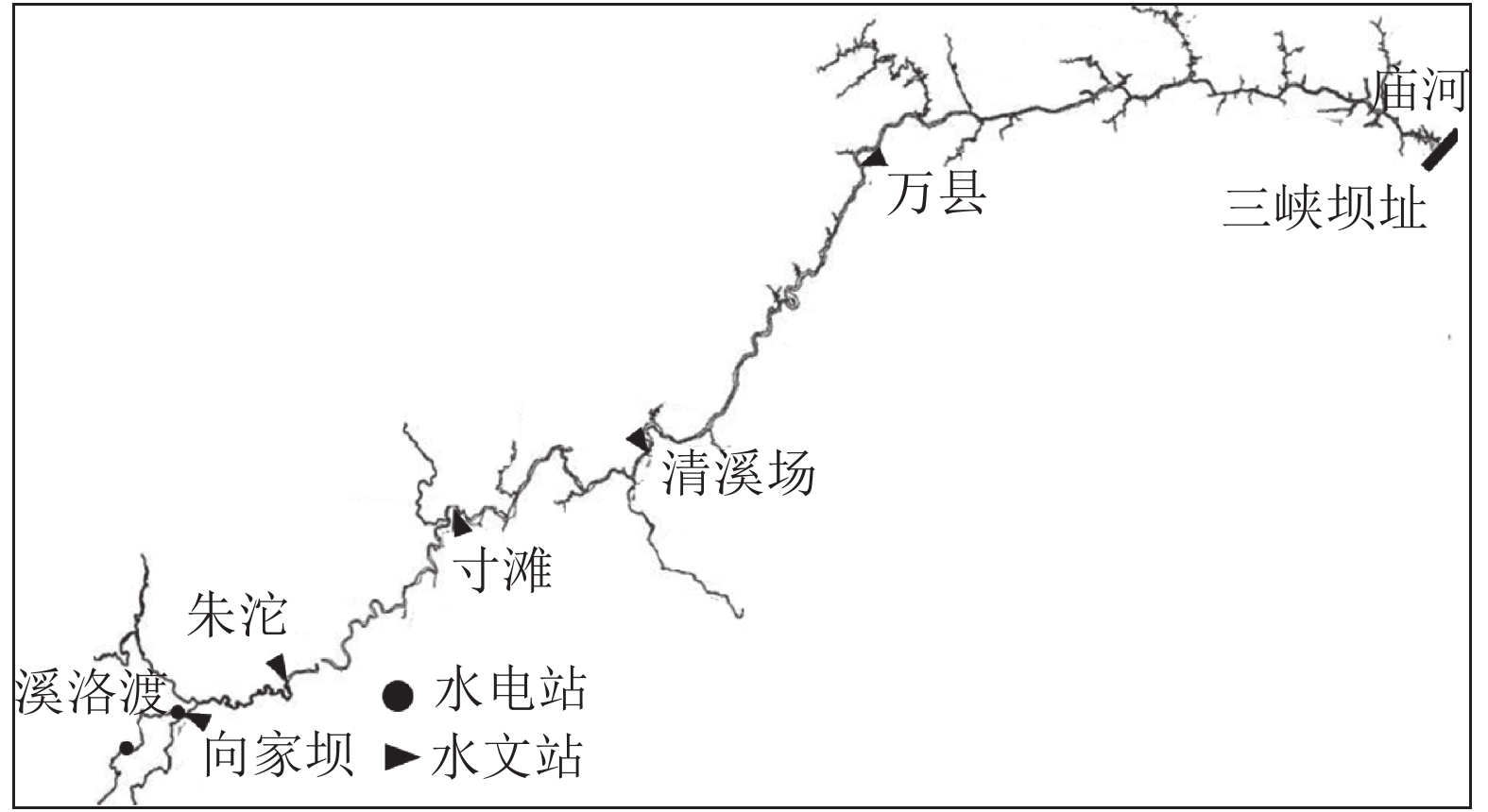 |
| 图1 三峡库区示意图 Fig. 1 Sketch map of Three Gorges Reservoir area |
1.2 研究资料及代表站选取
本文重点研究三峡水库泥沙淤积滞后响应规律,上游长江干流和嘉陵江为三峡水库来流来沙主要来源,寸滩站作为长江干流和嘉陵江汇入后的代表站,因此寸滩站为入库代表站,选取黄陵庙为出库代表站。研究资料为2003—2018年三峡水库入库(寸滩站)和出库(黄陵庙站)日均流量和含沙量、坝前水位以及入库(寸滩站)泥沙级配资料。
1.3 研究方法本文采用的研究方法为输沙率法[19-20]和滞后响应模型。基于三峡入库代表站(寸滩站)和出库代表站(黄陵庙站)的流量、含沙量资料,采用输沙率法计算水库泥沙淤积量。采用吴保生等[4]提出的滞后响应模型探究三峡水库泥沙淤积滞后响应规律。
依据变率方程,河道调整速率与河道调整特性量的当前值和其平衡值之间的差值成正比[12,21],方程如下:
| ${{{\rm{d}}y} / {{\rm{d}}t}} = \beta \left( {y_{\rm{e}} - y} \right)$ | (1) |
式中:
单步解析模式:
| $y = {y_{\rm{0}}}{{\rm{e}}^{ - \beta t}} + (1 - {{\rm{e}}^{ - \beta t}}){y_{\rm{e}}}$ | (2) |
多步递推模式:
| ${\quad\quad\;\;\; y_{{n}}} = (1 - {{\rm{e}}^{( - \beta \Delta t)}})\sum\limits_{i = 1}^n {({{\rm{e}}^{ - \left( {n - i} \right)\beta \Delta t}}){y_{{{\rm{e}}_{{{\boldsymbol{i}}}}}}}{\rm{ }}} + {{\rm{e}}^{( - n\beta \Delta t)}}{y_{{{\rm{e}}_{\rm{0}}}}}{\rm{ }}$ | (3) |
故本文选择多步递推模式构建泥沙淤积滞后响应模型并采用构建的模型进行进一步分析。
此外,梯级水库于2012年正式蓄水运行,因此研究时段共选取2003—2018年、2003—2012年以及2013—2018年3个时段。
2 三峡水库水沙条件与泥沙淤积特性泥沙淤积滞后响应规律与水沙条件及泥沙淤积特性有关,为了分析梯级水库蓄水前后三峡水库泥沙淤积滞后响应规律,首先分析三峡水库的水沙条件变化及泥沙淤积特性。
2.1 来水来沙条件变化金沙江下游梯级水库蓄水拦截泥沙,三峡水库入库输沙量大幅度减少,径流量变化不大,见图2。如图2所示,汛期入库流量略微降低(8%),入库沙量大幅度降低(67%),同时,汛期入库流量的波动范围减小(47 040~32 158 m3/s),含沙量的波动范围也减小(2.65~1.47 kg/m3)。梯级水库蓄水后,汛期来沙占全年来沙比重有所增加(89.87%~90.84%),汛期来流占全年比重有所降低(60.90%~57.63%),即三峡水库入库来沙更加集中在汛期。
 |
| 图2 寸滩站汛期水沙条件变化 Fig. 2 Change process of suspended sediment and flow in the flood event of Cuntan Station |
2.2 泥沙淤积特点
梯级水库蓄水后,由于三峡水库入库泥沙减少,三峡库区年泥沙淤积量及汛期泥沙淤积量均减少,减少幅度达62.3%,因此整个三峡水库汛期泥沙累计淤积速率有所降低,而三峡水库汛期泥沙淤积占全年泥沙淤积比重有所增加(87.70%~91.18%)。梯级水库蓄水后,三峡水库汛期泥沙淤积量降低,汛期泥沙淤积占比增加,如图3所示。
 |
| 图3 库区年、汛期淤积及汛期占比 Fig. 3 Sedimentation in the whole year and flood season and the proportion in flood season |
3 三峡水库泥沙淤积滞后响应规律
吴保生[4-5]曾在研究水库泥沙淤积时提出库区泥沙淤积滞后响应模型,并将其运用在三门峡水库泥沙淤积的研究中,该模型采用流量加权平均坝前水位得到库区泥沙平衡淤积量的计算式,如式(4)所示:
| ${V_{\rm{e}}} = K\overline {\textit{Z}}_{\rm{d}}^{\rm{b}} + {V_*}$ | (4) |
式中:
| ${V_{{n}}} = \left(1 - {{\rm{e}}^{( - \beta \Delta t)}}\right)\sum\limits_{i = 1}^n {\left({{\rm{e}}^{ - \left( {n - i} \right)\beta \Delta t}}\overline {\textit{Z}}_{{{\rm{d}}_{{{\boldsymbol{i}}}}}}^{\rm{b}}\right){\rm{ }}} + K{{\rm{e}}^{( - n\beta \Delta t)}}\overline {\textit{Z}}_{{{\rm{d}}_{\rm{0}}}}^{\rm{b}} + {V_*}$ | (5) |
将式(5)用于三峡水库泥沙淤积滞后响应规律的研究中,参数及结果如表1所示。表1中:K为系数;β为调整系数;N为前期影响时间,a。
| 表1 计算式(5)模拟参数及计算精度 Tab. 1 Parameters and calculation accuracy used for Eq. (5) |
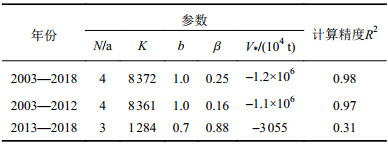 |
从表1得到:式(5)模拟梯级水库蓄水前三峡水库泥沙累积淤积过程结果较好(R2=0.97)。梯级水库蓄水后三峡水库来水来沙发生变化,导致入库水沙的相关性变差(R2为0.7859~0.3067),如图4所示,仅采用入库流量过程无法反映入库沙量变化对于库区泥沙淤积的影响,故重新建立符合三峡水库泥沙淤积特性的滞后响应模型,利用改进后的模型开展三峡水库泥沙淤积滞后响应规律的相关研究。
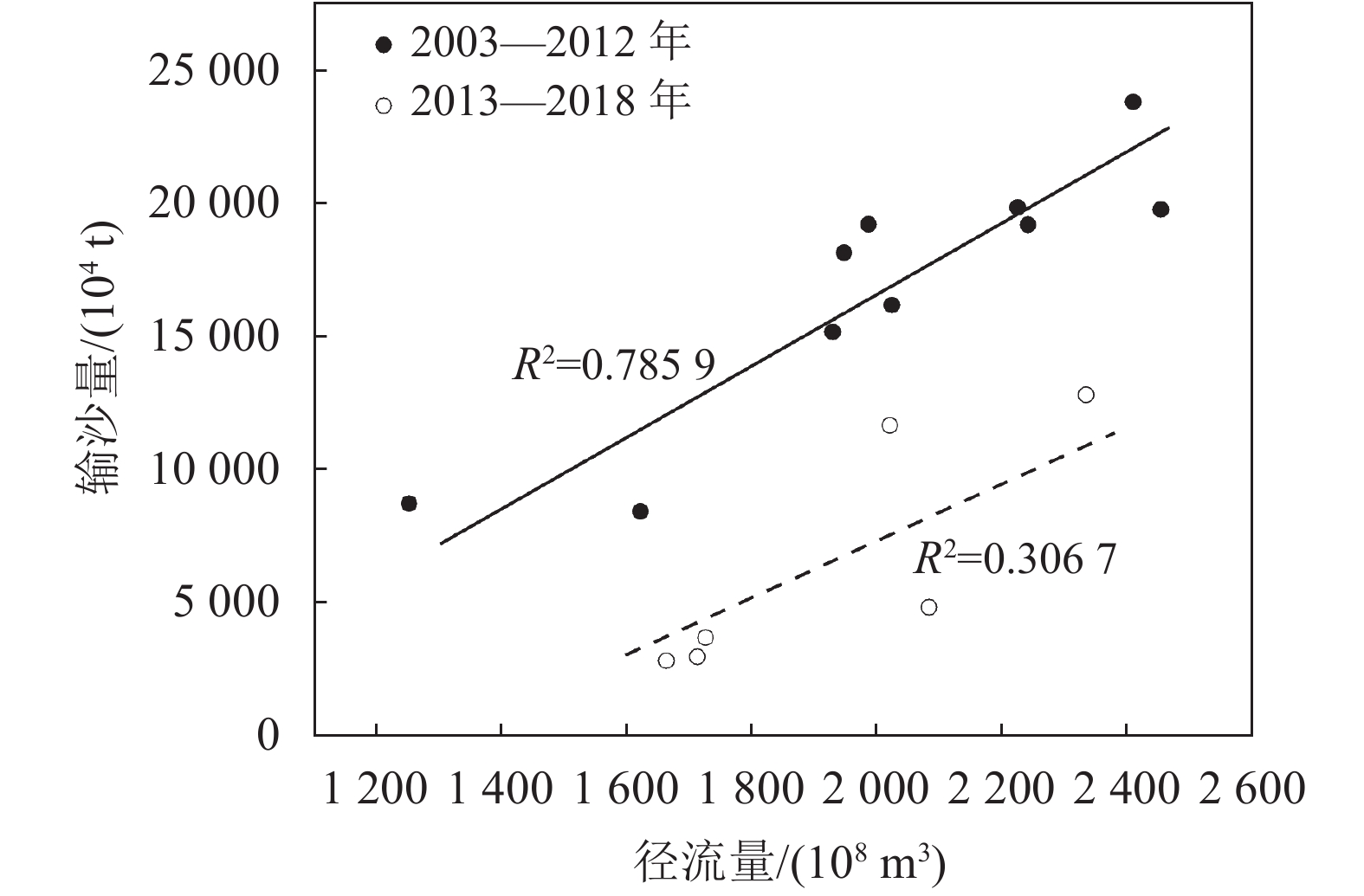 |
| 图4 三峡水库入库水沙关系 Fig. 4 Relationship between the flow and the sediment in the incoming water of TGR |
3.1 三峡水库泥沙淤积滞后响应模型
已有的库区泥沙淤积滞后响应模型无法较好地模拟梯级水库蓄水后三峡水库泥沙累积淤积过程,因此,需构建符合三峡水库泥沙淤积特点的滞后响应模型,以分析梯级水库蓄水前后三峡水库泥沙累积淤积滞后响应规律及其变化。
3.1.1 模型建立三峡库区泥沙淤积变化与入库水沙条件变化[22]、水库调度方式有关[23]。由前面第2.1节水沙条件统计可以发现:梯级水库蓄水后三峡水库汛期入库流量和入库含沙量均减少,来沙更加集中在汛期。入库水沙条件的变化对库区泥沙淤积影响不能忽视,同时,还需要考虑泥沙级配、水深和河道边界条件等对库区泥沙冲淤的影响[24]。使用张瑞瑾[25]提出的水流挟沙力公式:
| ${S_*} = K{\left(\frac{{{U^3}}}{{gR\omega }}\right)^m}$ | (6) |
式中:
| $\omega = \dfrac{1}{{24}}\left(\dfrac{{{\gamma}_ {\rm{s}} - \gamma }}{\gamma }\right)g\dfrac{{{d^2}}}{\upsilon } $ | (7) |
式中:γs 为泥沙颗粒重度,N/m3 ;γ为水的重度,N/m3 ;υ为水的运动黏滞性系数,m2/s。
将式(7)代入式(6)得:
| ${\;\;\;\;\;\;S_*} = K{\left( {\frac{{{Q^3}}}{{\alpha g{B^3}H_0^4\omega }}} \right)^m} = K{\left( {\frac{{24\gamma \upsilon }}{{\alpha \left( {\gamma_{\rm{s}} - \gamma } \right){g^2}}}\frac{{{Q^3}}}{{{B^3}H_0^4{d^2}}}} \right)^m}$ | (8) |
式中:
根据式(8)可以发现,水流挟沙力与
当三峡水库入库水沙条件、坝前水位等保持不变时,经过较长时间的冲淤调整,最终会形成与水沙条件等相适应的库区泥沙冲淤平衡状态,此时的泥沙淤积量则为三峡水库的平衡淤积量。这里选用挟沙强度
| ${\;\;\;\;\;\;\;\;\;\;\;V_{\rm{e}}} = K\frac{{{S^b}}}{{{{\left( {{{{Q^3}} / {H_0^4{d^2}}}} \right)}^\alpha }}} = K{Q^A}{S^B}{d^C}{(LH)^M}$ | (9) |
式中:K、A、B、C、L、M为系数,
| ${V_n} = \left(1 - {{\rm{e}}^{( - \beta \Delta t)}}\right)\sum\limits_{i = 1}^n {\left({{\rm{e}}^{ - \left( {n - i} \right)\beta \Delta t}}\right)KQ_i^AS_i^Bd_i^C{{\left( {L{H_i}} \right)}^M}){\rm{ }}} + {{\rm{e}}^{\left( - n\beta \Delta t\right)}}{V_0}{\rm{ }}$ | (10) |
式(10)为三峡水库泥沙累积淤积滞后响应模型的计算公式。模型通过迭代考虑了前期影响和滞后响应,同时考虑水沙条件变化、水库调度方式变化(坝前水位变化)对水库泥沙累计淤积的协同作用。
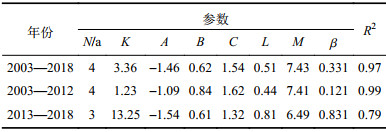
3.1.2 参数率定及模型验证采用式(10)对三峡水库泥沙累积淤积过程进行拟合,参数如表2所示。
| 表2 计算式(10)模拟参数及计算精度 Tab. 2 Parameters and calculation accuracy used for Eq. (10) |
 |
根据冲积性河道的自动调整原理[26]可以发现,河道自动调整作用的速率相较水沙条件等变化要慢很多,因此河道在受到外部扰动后恢复到新的平衡状态往往需要较长的时间[4],对于泥沙淤积滞后响应的过程也同样如此。将拟合得到的参数代入式(10)中得到特征量计算值,通过对比计算值及实测值得到不同前期影响年数N的模型计算精度R2值和相对误差,其结果如图5所示。
 |
| 图5 泥沙淤积滞后响应模型模拟结果 Fig. 5 Simulation results of the delayed response model for sedimentation |
由于泥沙累积淤积是一个滞后时段相对较长的过程,因此,当前期影响年数N较小时,其滞后响应规律尚未完全体现;当前期影响年限N较大时,在距离当年较远的年份对当前河床演变过程中滞后响应的影响已经削弱甚至消失。故认为计算精度R2稳定在最大值或者相对误差最小时的N即为累计淤积量受前期水沙条件影响最大的年数(实际影响年数为N+1 a)。根据上述要求选择前期影响年限N为滞后响应年限。
对比已有模型及优化后模型的模拟结果表1和2得到:梯级水库蓄水前,三峡水库来水来沙符合“大水大沙、小水小沙”的特性,可以采用流量过程代替沙量过程进行拟合,已有模型及优化后的模型模拟梯级水库蓄水前三峡水库泥沙累积淤积过程效果均较好。梯级水库蓄水后,来水来沙特性发生较大变化,优化后的模型考虑了含沙量及泥沙粒径的影响,能够更真实地反映梯级水库蓄水后三峡水库泥沙累计淤积过程,优化后模型的模拟精度较已有模型的精度有较大提高(R2从0.31提高到0.79)。
根据图5(a)、(b)和(c)可以看出:当N=4时,模型拟合2003—2012年泥沙累计淤积效果最佳(R2=0.99,相对误差5.95%),三峡水库泥沙淤积与前期4 a的水沙条件、坝前水位有关。当N=3时,模拟2013—2018年泥沙累积淤积效果最佳(R2=0.79,相对误差2.14%),三峡水库泥沙淤积与前期3 a的水沙条件、坝前水位有关。梯级水库蓄水后,三峡水库泥沙淤积的滞后响应年限从前期4 a缩短到前期3 a。
3.1.3 计算结果分析梯级水库蓄水后,三峡水库泥沙淤积的滞后响应年限从前期4 a缩短到前期3 a。对于河道系统而言,外部控制条件所受扰动越剧烈,整个河道系统通过自动调整作用吸收外部扰动时间越长,河道的自动调整速率越慢,表现为滞后响应年限越长[4]。
从河道调整速率而言,河道系统在受到外界干扰后,河道调整速率越快,消除外界干扰的影响所需要的时间更短[27]。滞后响应模型中参数β反映的是河道在某时刻的调整能力,在以往的研究发现,调整速率β与汛期来水来沙占全年来水来沙的集中程度有关,汛期来沙越集中,来流更分散,调整速率越大[13]。梯级水库蓄水后,汛期来水来沙不符合“大水多沙、小水少沙”的规律,汛期来沙更加集中,汛期来流表现则相反,因此汛期泥沙淤积的调整速率更大(β从0.121增加到0.831),河道自动调整的时间尺度有所压缩,表现为泥沙淤积的滞后响应时间缩短。
从外部扰动的影响而言,对于三峡水库河道系统而言,外部控制条件(来水来沙)受上游降雨、人类活动等的影响不断变化[1,28-30]。梯级水库蓄水后,三峡水库入库水沙变幅均有所减小(汛期流量波动范围为47 040.0~32 158.3 m3/s,汛期含沙量波动范围为2.65~1.47 kg/m3),即来水来沙受到扰动相对减弱,外部控制条件(来水来沙)趋于“相对稳定”,整个三峡水库泥沙淤积的滞后响应时间缩短。
综上所述,得到梯级水库蓄水后,水沙条件变化(变幅减小、来沙更集中在汛期)导致汛期泥沙淤积调整速率增加,泥沙淤积滞后响应年限从前期4 a缩短到前期3 a。
3.2 三峡水库泥沙淤积滞后响应规律分析为了进一步说明入库水沙条件及坝前水位变化对三峡水库泥沙累积淤积过程影响,采用已经建立的模型进行敏感性分析。由于根据已有的资料无法确定泥沙粒径的波动范围,因此主要针对汛期入库流量、含沙量以及坝前水位对库区泥沙淤积的影响进行探讨。对于不同设计条件的选取,以设计坝前水位
| 表3 不同工况2012年和2018年泥沙淤积量计算值 Tab. 3 Calculation values of sediment deposition in 2012 and 2018 under different design conditions |
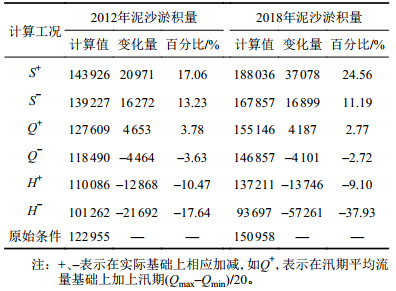 |
根据表3可以发现:梯级水库蓄水后,汛期入库含沙量对于库区泥沙淤积的影响程度有所增加(17.35%~31.25%),汛期入库流量影响程度均有所降低(11.850%~10.145%),坝前水位的影响程度略微降低(3.705%~2.745%)。
泥沙冲淤变化与水沙条件变化密切关系。第2.1节水沙条件分析得到梯级水库蓄水后,三峡水库泥沙淤积仍然以汛期为主,但汛期入库来沙占比增加(89.87%~90.84%),汛期来流占比降低(60.90%~57.63%),因此,入库含沙量对库区泥沙淤积的影响程度增加,相应的入库流量对库区泥沙淤积的影响程度降低。
三峡水库自蓄水以来,库区水深较大且坝前水深可达百米级,汛期坝前水位日均变幅较库区平均水深小很多,同时汛期坝前水位升降历时较短,即汛期坝前水位波动对库区泥沙淤积影响时间短,故汛期坝前水位对汛期库区泥沙淤积的影响程度最小。
总体而言,汛期三峡水库泥沙累计淤积过程主要受汛期入库含沙量的影响,其次是汛期入库流量,汛期平均坝前水位影响最小。梯级水库蓄水后,三峡水库汛期入库含沙量对于库区泥沙淤积的影响程度增加,对入库流量及坝前水位对库区泥沙淤积的影响程度降低。
4 结 论本文在分析三峡水库水沙条件变化、泥沙淤积特性基础上,分析了已有水库泥沙淤积滞后响应模型模拟效果,建立了符合三峡水库泥沙累积淤积特征的泥沙淤积滞后响应模型对三峡水库泥沙淤积滞后响应规律进行研究,并初步分析了梯级水库蓄水对三峡水库泥沙淤积的影响,得到如下结论:
1)金沙江下游梯级水库蓄水后,三峡水库汛期入库水沙条件发生较大变化,主要表现为汛期入库流量略微降低(8%)、入库沙量大幅度降低(67%),同时汛期入库流量波动范围减小(47 040.0~32 158.3 m3/s),含沙量波动范围减小(2.65~1.47 kg/m3),汛期来沙更为集中,汛期泥沙淤积量有所降低,泥沙累积淤积速率降低,但汛期泥沙淤积占比增加3.50%(87.70%~91.18%)。
2)在已有库区泥沙淤积滞后响应模型基础上,考虑入库流量、含沙量、泥沙中数粒径以及坝前水位建立了符合三峡水库泥沙淤积特性的滞后响应模型。优化后的泥沙淤积滞后响应模型与已有模型相比能够更好地模拟三峡水库泥沙淤积变化(梯级水库蓄水前后R2分别为0.99和0.79)。
3)基于上述模型揭示了三峡水库泥沙淤积滞后响应规律,并探讨了梯级水库蓄水对三峡水库泥沙淤积的影响。梯级水库蓄水后,三峡入库来沙更加集中在汛期,河道调整速率加剧,河道调整的时间尺度有所缩短,表现为三峡库区泥沙淤积与水沙过程滞后响应年限由前期4 a缩减到前期3 a。三峡水库汛期入库含沙量对整个库区泥沙淤积影响程度增加,汛期入库流量及坝前水位对库区泥沙淤积影响程度降低。
对于三峡水库而言,目前蓄水至今仅十余年,实测资料相对有限,基于现有的条件进行初步分析,定性上得到如下规律:金沙江下游梯级水库蓄水后,三峡水库来沙更加集中在汛期,汛期入库含沙量对于整个河道调整作用影响程度增加,河道调整速率加剧,三峡水库泥沙淤积的滞后响应时间尺度有所缩短。待实测资料丰富后,可进一步对三峡水库泥沙淤积滞后响应规律进行更为深入的研究。
| [1] |
Hu Chunhong,Fang Chunming. Research on sediment problem solutions for the Three Gorges project and it operational effects[J]. Scientia Sinica Technologica, 2017, 47(8): 832-844. [胡春宏,方春明. 三峡工程泥沙问题解决途径与运行效果研究[J]. 中国科学(技术科学), 2017, 47(8): 832-844.] |
| [2] |
Hu Chunhong,Fang Chunming,Xu Quanxi. Application and optimization of “storing clean water and discharging muddy flow” in the Three Gorges Reservoir[J]. Journal of Hydraulic Engineering, 2019, 50(1): 2-11. [胡春宏,方春明,许全喜. 论三峡水库“蓄清排浑”运用方式及其优化[J]. 水利学报, 2019, 50(1): 2-11.] |
| [3] |
Knighton D.Fluvial forms and processes[M].New York:Earth Science Reviews,1996.
|
| [4] |
Wu Baosheng. Delayed response model for fluvial processes of alluvial rivers—Ⅰ model development[J]. Journal of Sediment Research, 2008(6): 1-7. [吴保生. 冲积河流河床演变的滞后响应模型—Ⅰ模型建立[J]. 泥沙研究, 2008(6): 1-7. DOI:10.3321/j.issn:0468-155X.2008.06.001] |
| [5] |
Wu Baosheng. Delayed response model for fluvial processes of alluvial rivers—Ⅱ model applications[J]. Journal of Sediment Research, 2008(6): 30-37. [吴保生. 冲积河流河床演变的滞后响应模型—Ⅱ模型应用[J]. 泥沙研究, 2008(6): 30-37. DOI:10.3321/j.issn:0468-155X.2008.06.005] |
| [6] |
Wu Baosheng,Zheng Shan,Shen Yi. Erosion and deposition in Sanmenxia Reservoir and the impacts of “318 Operation”[J]. Water Resources and Hydropower Engineering, 2020, 51(11): 1-12. [吴保生,郑珊,沈逸. 三门峡水库冲淤与“318运用”的影响[J]. 水利水电技术, 2020, 51(11): 1-12.] |
| [7] |
Yang Guangbin,Wu Baosheng,Zhang Ruoyin,et al. Influence of “318”controlled operation of the Sanmenxia Reservoir on variations of the Tongguan Elevation[J]. Journal of Sediment Research, 2020, 45(3): 38-45. [杨光彬,吴保生,章若茵等. 三门峡水库“318”控制运用对潼关高程变化的影响[J]. 泥沙研究, 2020, 45(3): 38-45.] |
| [8] |
Wu Baosheng. Delayed response model for bankfull discharge of alluvial rivers[J]. Journal of Hydraulic Engineering, 2008, 39(6): 680-687. [吴保生. 冲积河流平滩流量的滞后响应模型[J]. 水利学报, 2008, 39(6): 680-687. DOI:10.3321/j.issn:0559-9350.2008.06.007] |
| [9] |
Wu Baosheng. Delayed response model for bankfull area of the Gaocun Station on the lower Yellow River[J]. Journal of Sediment Research, 2010(2): 31-34. [吴保生. 黄河下游高村站平滩面积的滞后响应模型[J]. 泥沙研究, 2010(2): 31-34.] |
| [10] |
Shao Wenwei,Wu Baosheng,Wang Yanjun,et al. Simulation of sedimentation processes in dry and wet seasons in the Xiaobeiganliu reach of the Yellow River[J]. Acta Geographica Sinica, 2018, 73(5): 880-892. [邵文伟,吴保生,王彦君,等. 黄河小北干流汛期和非汛期冲淤过程模拟[J]. 地理学报, 2018, 73(5): 880-892. DOI:10.11821/dlxb201805008] |
| [11] |
Zheng Shan,Wu Baosheng,Hou Suzhen,et al. Spatial and temporal erosion and deposition processes and the delayed response of the Sanmenxia reservoir[J]. Journal of Hydraulic Engineering, 2019, 50(12): 1433-1445. [郑珊,吴保生,侯素珍,等. 三门峡水库时空冲淤与滞后响应[J]. 水利学报, 2019, 50(12): 1433-1445.] |
| [12] |
Zheng Shan,Wu Baosheng. Simulation of sediment processes of the Xiaobeiganliu reach of the Yellow River and the lower Wei River[J]. Journal of Hydraulic Engineering, 2014, 45(2): 150-162. [郑珊,吴保生. 黄河小北干流和渭河下游淤积过程模拟[J]. 水利学报, 2014, 45(2): 150-162.] |
| [13] |
Lv Yiwei,Tan Guangming,Zheng Shan,et al. Improvement of river evolution delay response model in the Jingjiang Reach[J]. Journal of Sediment Research, 2018, 43(1): 9-14. [吕宜卫,谈广鸣,郑珊,等. 荆江河段河床冲淤计算滞后响应模型改进[J]. 泥沙研究, 2018, 43(1): 9-14.] |
| [14] |
李凌云,吴保生. 黄河下游平滩流量的估算方法[J]. 人民黄河, 2009, 31(6): 32-33. DOI:10.3969/j.issn.1000-1379.2009.06.013 |
| [15] |
Li Lingyun,Wu Baosheng. Modification of delayed response model for bankfull discharges[J]. Journal of Sediment Research, 2011(2): 21-26. [李凌云,吴保生. 平滩流量滞后响应模型的改进[J]. 泥沙研究, 2011(2): 21-26.] |
| [16] |
Li Lingyun,Wu Baosheng,Hou Suzhen. Application of delayed response model to bankfull discharge in the Inner Mongolia reach of Yellow River[J]. Journal of Hydroelectric Engineering, 2011, 30(1): 70-77. [李凌云,吴保生,侯素珍. 滞后响应模型在黄河内蒙古河段的应用[J]. 水力发电学报, 2011, 30(1): 70-77.] |
| [17] |
Tang Xiaoya,Tong Sichen,Xu Guangxiang,et al. Delayed response of sedimentation in the flood seasons to the pool level of the Three Gorges Reservoir[J]. Advances in Water Science, 2019, 30(4): 528-536. [唐小娅,童思陈,许光祥,等. 三峡水库汛期泥沙淤积对坝前水位的滞后响应[J]. 水科学进展, 2019, 30(4): 528-536.] |
| [18] |
张洪记,陈磊,黄仁勇. 溪洛渡、向家坝建库对三峡水库淤积影响计算研究[J]. 中国水运(下半月), 2019, 19(4): 166-167. |
| [19] |
Dai S B,Lu X X. Sediment load change in the Yangtze River(Changjiang):A review[J]. Geomorphology, 2014(215): 60-73. |
| [20] |
Yang H F,Yang S L,Xu K H,et al. Human impacts on sediment in the Yangtze River:A review and new perspectives[J]. Global and Planetary Change, 2018(162): 8-17. |
| [21] |
Zheng Shan,Wu Baosheng,Tan Guangming. Review on the self-adjustment behavior of alluvial rivers based on the concept of marco system[J]. Journal of Sediment Research, 2014(5): 73-80. [郑珊,吴保生,谈广鸣. 基于宏观系统的冲积河流自动调整研究评述[J]. 泥沙研究, 2014(5): 73-80.] |
| [22] |
Chen Jian,Li Yitian,Deng Jinyun,et al. Influence on deposition of the Three Gorges Reservoir caused by the change of water silt conditions[J]. Journal of Hydroelectric Engineering, 2008, 27(2): 97-102. [陈建,李义天,邓金运,等. 水沙条件变化对三峡水库泥沙淤积的影响[J]. 水力发电学报, 2008, 27(2): 97-102. DOI:10.3969/j.issn.1003-1243.2008.02.019] |
| [23] |
Li Wei. Influence of reservoir operation scheduling operation mode on reservoir sediment deposition[J]. Water Resources Development & Management, 2017, 37(9): 65-67. [李巍. 水库调度运行方式对水库泥沙淤积的影响[J]. 水利建设与管理, 2017, 37(9): 65-67.] |
| [24] |
Liu Jie,Yang Shengfa,Sheng Ying. Impact of runoff and sediment from the upper Yangtze River on deposition in the Three Gorges Reservoir[J]. Journal of Sediment Research, 2019, 44(6): 33-39. [刘洁,杨胜发,沈颖. 长江上游水沙变化对三峡水库泥沙淤积的影响[J]. 泥沙研究, 2019, 44(6): 33-39.] |
| [25] |
张瑞瑾.河流泥沙动力学[M].北京:中国水利水电出版社, 2008:159−161.
|
| [26] |
钱宁,张仁,周志德.河床演变学[M].北京:科学出版社.1987.
|
| [27] |
Dang M H,Umeda S,Yuhi M. Long-term riverbed response of lower Tedori River,Japan,to sediment extraction and dam construction[J]. Environment Earth Sciences, 2014, 72(8): 2971-2983. DOI:10.1007/s12665-014-3202-0 |
| [28] |
Zhu Lingling,Dong Xianyong,Chen Zefang. Sediment deposition of cascade reservoirs in the lower Jinsha River and its impact on Three Gorges Reservoir[J]. Journal of Yangtze River Scientific Research Insitute, 2017, 34(3): 1-7. [朱玲玲,董先勇,陈泽方. 金沙江下游梯级水库淤积及其对三峡水库影响研究[J]. 长江科学院院报, 2017, 34(3): 1-7. DOI:10.11988/ckyyb.20160007] |
| [29] |
Xiao Yi,Yang Shengfa,Shao Xuejun. Trends of temporal variation of the flow-sediment discharges into the Three Gorges Reservoir[J]. Journal of Sediment Research, 2017, 42(6): 22-27. [肖毅,杨胜发,邵学军. 三峡水库水沙条件时序变化趋势研究[J]. 泥沙研究, 2017, 42(6): 22-27.] |
| [30] |
Du Jun,Shi Changxin,Zhang Shouhong,et al. Impact of human activities on rencent changes in sediment discharge of the upper Yangtze River[J]. Progress in Geography, 2010, 29(1): 15-22. [杜俊,师长兴,张守红,等. 人类活动对长江上游近期输沙变化的影响[J]. 地理科学进展, 2010, 29(1): 15-22. DOI:10.11820/dlkxjz.2010.01.003] |
 2021, Vol. 53
2021, Vol. 53

