2. 河北省电磁环境效应与信息处理重点实验室,河北 石家庄 050043
2. Hebei Key Lab. of Electromagnetic Environment Effects and Info. Processing, Shijiazhuang 050043, China
频控阵(FDA)雷达概念是2006年由Antonik等[1]首次提出的,和传统的相控阵雷达相比,其阵列因子的数学模型中包含了距离、角度和时间3个变量,从而能够形成具有距离依赖特性的时变发射波束。王文钦等[2]是国内最早进行相关研究的学者之一。
发射波束合成是频控阵雷达的主要研究热点之一。当FDA雷达发射信号采用线性频率增量时,其辐射“S”状时变波束,该波束可以完成空间区域扫描,但是,由于其在距离角度维的缠绕和时变特性导致其波束指向难以控制。因此,部分学者对点状波束形成和独立于时间的静态波束形成问题进行了深入研究。Wang[3]提出了一种FDA离散椭球序列波束方向图设计策略,通过设计发射波束空间权重向量,使得期望2维空间的辐射能量与阵列雷达总的辐射能量的比值最大化。Shao等[4]提出了一种凸优化多载频对数频率增量方法合成了单、多点状发射波束。Xu等[5]采用二阶锥规划实现了点状波束的合成。Xiong等[6]采用遗传算法优化频率增量完成了点状波束合成。Chen等[7]提出了一种拉格朗日规划神经网络方法用于发射波束的聚焦。Wang[8]、王博[9]等进一步研究了基于对数频率增量线性重叠子阵与多载频重叠面阵的点状波束合成,分析了基于SD–LCMV算法的log–FDA、cubic–FDA、sin–FDA和倒数FDA结构的波束距离–角度解耦性能。虽然文献[3-9]中可以成功合成点状波束,但其在仿真分析中都是采用固定时间项,即忽略波束的时变特性,没有考虑波的传播特性。
为了解决上述问题,Xu等[10]提出了一种脉冲FDA发射波束合成方法,通过合理设置脉冲持续时间和频率增量实现了准静态波束合成。Khan等[11]提出了时间调制频率增量技术,其在指定位置处合成的发射波束仅在脉冲持续时间内是不变的,在其他位置处的波束仍然是时变的。Yao等[12]采用基于时间调制的非线性频率增量实现了空间时不变聚焦波束。Wang等[13]提出了一种时不变距离角度维解耦的FDA发射波束合成方法;在该方法中,每个阵元辐射的信号为多个时间调制非线性频率增量信号的加权和。Liao等[14]研究了对称对数间隔分布阵列的多载频点状波束合成,其频率采用时间调制,但没有考虑电磁波的传播,即没有考虑波的时变性。在数学上,文献[11-14]中的方法很好地解决了点状波束的时变问题,即可使FDA合成的波束在空间保持静态,从而使得波束在目标处的驻留时间变长,目标反射能量可得到很好的积累,提高探测概率。但是,文献[11-14]中没有清晰阐述频率增量项时间变量和波形传播项时间变量的关系,而是将其看成同一个变量。Shi等[15]从时间和距离关系的角度分析并得出FDA不可能合成时不变波束方向图的研究结果,但并未研究点状波束合成问题。
此外,利用FDA波束形成优势与MIMO体制相结合的研究也得到了快速发展,例如,采用FDA–MIMO收发波束精确消零技术对SAR成像中的干扰进行抑制[16-17],采用FDA–MIMO雷达进行参数估计、目标探测、成像等[18-21]。但是,FDA波束设计灵活性并未在这些应用中得到充分发挥。本文重点研究了FDA雷达发射波束时变特性和点状波束合成,构建了时间调制对数频率增量和多载频频率增量FDA雷达信号模型,分析并理清了时间调制FDA信号模型中频率增量项时间变量与传播项时间变量的关系,进一步分析了时间调制对数频率增量和多载频频率增量模式合成的点状发射波束的特性。
1 信号模型 1.1 线性频率增量FDA信号模型以1维线性阵列为例进行说明。假设阵列包含
| $ {\;\;\;\;\;\;\;f_n} = {f_0} + n\Delta f,\;n = 0,1, \cdots ,N - 1 $ | (1) |
式中,
第
| $ {s_n}(t) = {{\text{e}}^{{\text{j}}2{\text{π}}{f_n}t}} $ | (2) |
以第1个阵元为参考点,远场区域任意点
| $ \begin{aligned}[b] &{\boldsymbol E} = {\boldsymbol a}{E_P} = {\boldsymbol a}\sum\limits_{n = 0}^{N - 1} {{w_n}\frac{{{F_n}(\theta )}}{{{r_n}}}{{\text{e}}^{{\text{j}}2{\text{π}}{f_n}\left( {t - {\tau _n}} \right)}}} \approx \\ &\;\;{\boldsymbol a}\frac{{F\left( \theta \right)}}{r}{{\text{e}}^{{\text{j}}2{\text{π}}{f_0}\left( {t - \frac{r}{c}} \right)}}\sum\limits_{n = 0}^{N - 1} {{w_n}{{\rm e}^{{\text{j}}2{\text{π}}\left[ {n\Delta f\left( {t - \frac{r}{c}} \right) + \frac{{nd{f_{0}}\sin \;\theta }}{c} + \frac{{{n^2}\Delta fd\sin\; \theta }}{c}} \right]}}} \end{aligned} $ | (3) |
式中:
在FDA雷达中,阵列频率增量比载频小,所以,式(3)中第2行的求和号的指数第3项可以忽略[6],且该求和号内表达式与阵元辐射特性无关,与阵列结构和频率增量有关。频控阵的阵列因子(array factor, AF)用符号
| $ \begin{aligned}[b] {F_{{\text{AF}}}}(r,\theta ,t) =& {{\text{e}}^{{\text{jπ}}(N - 1)\left[ {\Delta f(t - r/c) + \frac{{{f_0}d\sin\; \theta }}{c}} \right]}} \times \\ &\frac{{\sin \left[ {N{\text{π}}\left( {\Delta f\left( {t - \dfrac{r}{c}} \right) + \frac{{d{f_0}\sin \;\theta }}{c}} \right)} \right]}}{{\sin \left[ {{\text{π}}\left( {\Delta f\left( {t - \dfrac{r}{c}} \right) + \frac{{d{f_0}\sin\; \theta }}{c}} \right)} \right]}} \end{aligned} $ | (4) |
阵列方向图为阵列因子的绝对值,由式(4)可知,线性频率增量FDA辐射方向图是时间
时间调制频率增量记为
| $ {s_n}(t) = {{\text{e}}^{{\text{j}}2{\text{π}}\left[ {{f_0} + \Delta {f_n}(t)} \right]t}},\;t \in \left[ {0,T} \right] $ | (5) |
则FDA阵列因子重写如下:
| $ {\;\;\;\;\;\;\;\;\;\;\;\;\begin{aligned}[b]{F_{{\text{AF}}}}(r,\theta ,t) = &\displaystyle\sum\limits_{n = 0}^{N - 1} {{w_n}{{\text{e}}^{{\text{j}}2{\text{π}}\left[ {\Delta {f_n}(t)\left( {t - \frac{r}{c}} \right) + \frac{{nd{f_{0}}\sin\; \theta }}{c}} \right]}}} , \\ &t \in [{\tau _n},{\tau _n} + T] \end{aligned}}$ | (6) |
式中,
时间调制频率增量和时间调制对数频率增量表达式可以分别表示为[11-12]:
| $ \Delta {f_n}(t) = \frac{{n - (n{f_0}d\sin\;{\theta _{\text{d}}}){\text{/}}c}}{{t - {r_{\text{d}}}/c}} $ | (7) |
| $ {\;\;\;\;\;\;\;\;\;\;\;\Delta {f_n}(t)} = \frac{{\ln {{(n + 1)}^\kappa } - (n{f_0}d\sin\; {\theta _{\text{d}}})/c}}{{t - {r_{\text{d}}}/c}} $ | (8) |
式中,
采用多载频时间调制频率增量,每个阵元辐射信号为多个时间调制非线性频率增量信号的加权和[4,13],频率增量和阵列因子可分别写为式(9)和(10):
| $ {\;\;\;\;\;\;\;\Delta {f_m}(t)} = \frac{{\ln {{(m + 1)}^\kappa }}}{{t - {r_{\text{d}}}/c}},\; m = 0,1, \cdots ,M - 1 $ | (9) |
| ${\;\;\;\;\begin{aligned}[b] {F_{{\text{AF}}}}(r,\theta ,t) =& \displaystyle\sum\limits_{n = 0}^{N - 1} {\displaystyle\sum\limits_{m = 0}^{M - 1} {{w_n}{w_m}{{\text{e}}^{{\text{j}}2{\text{π}}\left[ {\Delta {f_m}(t)\left( {t - \frac{r}{c}} \right) + \frac{{nd{f_0}\sin\; \theta }}{c}} \right]}}} } , \\ & t \in [{\tau _n},{\tau _n} + T] \end{aligned}}$ | (10) |
式中,
为分析方便,且统一表示式(7)和(8),用
| $ {\;\;\;\begin{aligned}[b]{F_{{\text{AF}}}}(r,\theta ,t) = &\displaystyle \sum\limits_{n = 0}^{N - 1} {{{\text{e}}^{{\text{j2π}}\left[ {\left( {\frac{{F(n)}}{{t - {r_{\text{d}}}/c}}(t - r/c) - F(n)} \right) + \frac{{nd{f_0}(\sin\; \theta - \sin\;{\theta _{\text{d}}})}}{c}} \right]}}} , \\ &\quad t \in [{\tau _n},{\tau _n} + T] \end{aligned}}$ | (11) |
用
| $ {\begin{aligned}[b]{F_{{\text{AF}}}}(r,\theta ,t) = &\displaystyle \sum\limits_{n = 0}^{N - 1} {\displaystyle \sum\limits_{m = 0}^{M - 1} {{{\text{e}}^{{\text{j}}2{\text{π}}\left[ {\left( {\frac{{F(m)}}{{t - {r_{\text{d}}}/c}}(t - r/c) - F(m)} \right) + \frac{{nd{f_0}(\sin\; \theta - \sin\; {\theta _{\text{d}}})}}{c}} \right]}}} } , \\ &\quad t \in [{\tau _n},{\tau _n} + T]\\[-10pt]\end{aligned}}$ | (12) |
频率增量项可进一步表示为式(11)中
从式(11)和(12)可以看出,当
| $ {\;\;\;\;\;\;\begin{aligned}[b]{F_{{\text{AF}}}} = &\displaystyle\sum\limits_{n = 0}^{N - 1} {\text{e}}^{{\text{j}}2{\text{π}}\left[ {\left( {\frac{{F(n)}}{{t' - {r_{\text{d}}}/c}}(t - r/c) - F(n)} \right) + \frac{{nd{f_0}(\sin\; \theta - \sin \;{\theta _{\text{d}}})}}{c}} \right]} , \\ &\;\;\;\;t' \in [0,T],\;t \in [{\tau _n},{\tau _n} + T] \end{aligned}}$ | (13) |
| $ {\begin{aligned}[b]{F_{{\text{AF}}}} = &\displaystyle\sum\limits_{n = 0}^{N - 1} {\displaystyle\sum\limits_{m = 0}^{M - 1} {{w_n}{w_m}{{\text{e}}^{{\text{j}}2{\text{π}}\left[ {\left( {\frac{{F(m)}}{{t' - {r_{\text{d}}}/c}}(t - \frac{r}{c}) - F(m)} \right) + \frac{{nd{f_0}(\sin\; \theta - \sin \;{\theta _{\text{d}}})}}{c}} \right]}}} } , \\ &\;\;\;\;t' \in [0,T]\text{,}t \in [{\tau _n},{\tau _n} + T]\\[-10pt] \end{aligned}}$ | (14) |
针对脉冲信号,波束最大值出现在脉冲宽度覆盖空间区域内的约束条件为:
| $ {t' - \frac{{{r_{\text{d}}}}}{c}} < T $ | (15) |
式中,
根据FDA阵列因子的特点,分别选择固定时间绘制方向图的空间分布和固定空间位置绘制其在时间上的变化规律。雷达参数设置为
 |
| 图1 FDA连续波时变“S”状波束图 Fig. 1 Time-varying continuous wave “S”-shaped beampattern |
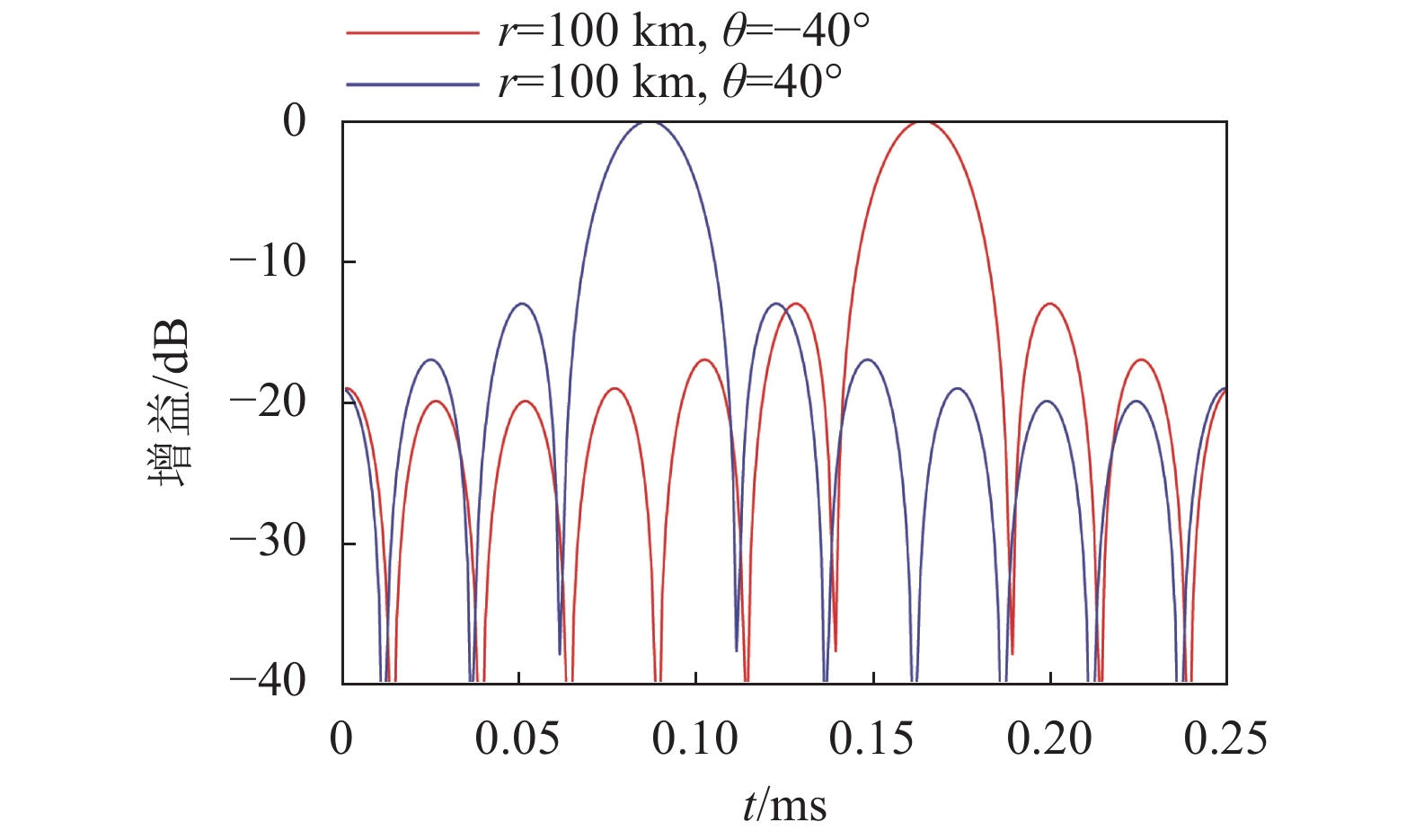 |
| 图2 空间确定位置波束随时间的变化 Fig. 2 Variation of beam with time for a specific spatially position |
3.2 时间调制频率增量波束图仿真
首先,对式(11)和(12)在不同时刻的连续波波束图仿真,雷达参数为
 |
| 图3 FDA时间调制对数频率增量连续波波束图 Fig. 3 FDA continuous wave beampattern with time-modulated logarithmic frequency offsets |
 |
| 图4 FDA时间调制多载频连续波波束图 Fig. 4 FDA continuous wave beampattern with time-modulated multi-carrier frequency increments |
从图3和4可以看出,在时间从0到0.225 ms变化过程中,发射波束始终聚焦于空间位置
然而,上述仿真所依据的模型式(11)和(12)中错误地将频率增量项中的时间变量与传播项中的时间变量等同且相互抵消,消除了波束的时变性。这具有很大的误导性,应当明确指出上述两个时间变量具有不同的物理意义。因此,时间频率调制的FDA 波束合成技术无法实现时不变空间点状波束。
进一步依据式(13)和(14),波形产生时刻变量
 |
| 图5 FDA对数频率增量脉冲动态点状波束图 Fig. 5 FDA pulse dynamic point-shaped beampattern with logarithmic frequency offsets |
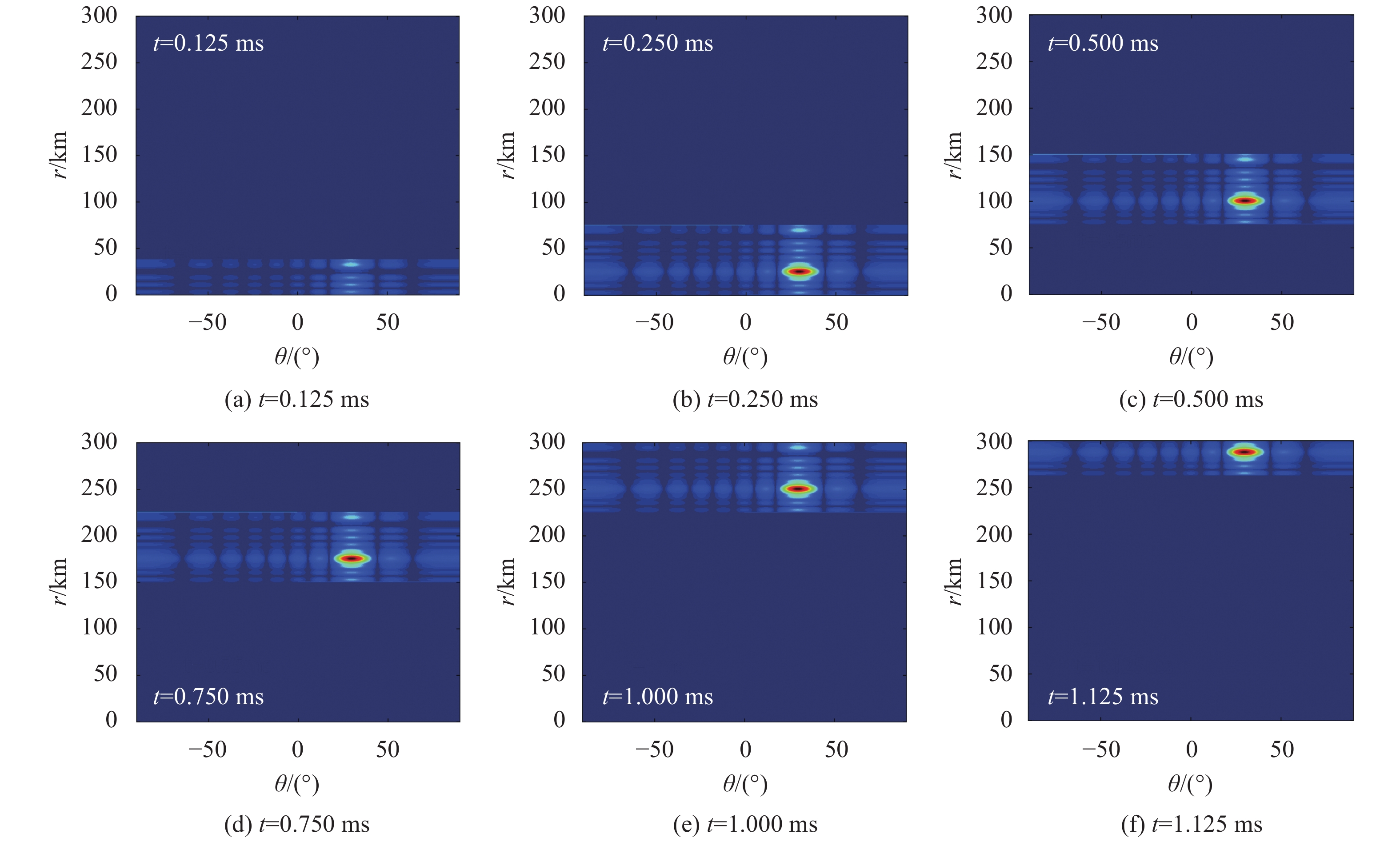 |
| 图6 FDA多载频非线性频率增量脉冲动态点状波束图 Fig. 6 FDA pulse dynamic point-shaped beampattern with multi-carrier frequency increments |
从图5和6的仿真结果可以看出:FDA阵列雷达通过合理的频偏设计可以合成点状波束。对数频率增量合成的点状波束旁瓣较高,且具有拖尾现象;多载频FDA合成的波束聚焦性能好,旁瓣低。无论哪种情况,点状波束在空间都是动态前向传播的,而不是静态时不变的。波束最大值会固定在方位
本文系统研究了采用时间调制频率增量技术合成空间时不变点状波束中存在的问题,分析并指出现有时间调制频率增量数学模型中频率增量项时间变量与传播项时间变量具有不同的物理意义。因此,不能简单地采用将这两项对消来消除发射波束的时变性。仿真结果验证了FDA雷达辐射脉冲信号且满足所给的约束条件时,可在脉冲覆盖空间区域内合成点状波束,该点状波束随时间动态前向传播,并非静态不动。在本文对FDA雷达波束合成研究的基础上,如何在干扰抑制、目标检测、雷达成像等方面发挥波束优势是下一步研究工作的重点。
| [1] |
Antonik P,Wicks M C,Griffiths H D,et al.Frequency diverse array radars[C]//Proceedings of the 2006 IEEE Conference on Radar.Verona:IEEE,2006:215–217.
|
| [2] |
Wang Wenqin,Shao Huaizong,Chen Hui. Frequency diverse array radar:Concept,principle and application[J]. Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011. [王文钦,邵怀宗,陈慧. 频控阵雷达:概念、原理与应用[J]. 电子与信息学报, 2016, 38(4): 1000-1011. DOI:10.11999/JEIT151235] |
| [3] |
Wang Wenqin. Range-angle dependent transmit beampattern synthesis for linear frequency diverse arrays[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(8): 4073-4081. DOI:10.1109/TAP.2013.2260515 |
| [4] |
Shao Huaizong,Dai Jun,Xiong Jie,et al. Dot-shaped range-angle beampattern synthesis for frequency diverse array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1703-1706. DOI:10.1109/LAWP.2016.2527818 |
| [5] |
Xu Yanhong,Shi Xiaowei,Li Wentao,et al. Flat-top beampattern synthesis in range and angle domains for frequency diverse array via second-order cone programming[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1479-1482. DOI:10.1109/LAWP.2015.2513758 |
| [6] |
Xiong Jie,Wang Wenqin,Shao Huaizong,et al. Frequency diverse array transmit beampattern optimization with genetic algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 16: 469-472. DOI:10.1109/LAWP.2016.2584078 |
| [7] |
Chen Tianfang,Xia Deping. Lagrange programming neural network approach for frequency diverse array beampattern synthesis[J]. Circuits,Systems,and Signal Processing, 2020, 39(1): 439-455. DOI:10.1007/s00034-019-01193-z |
| [8] |
Wang Bo,Xie Junwei,Zhang Jing,et al. Dot-shaped beamforming analysis based on OSB log–FDA[J]. Journal of Systems Engineering and Electronics, 2020, 31(2): 312-320. DOI:10.23919/JSEE.2020.000009 |
| [9] |
Wang Bo,Xie Junwei,Zhang Jing,et al. Frequency diverse array beam control based on nonlinear frequency offset[J]. Transactions of Beijing Institute of Technology, 2019, 39(3): 311-319. [王博,谢军伟,张晶,等. 基于非线性频偏的频控阵波束控制研究[J]. 北京理工大学学报, 2019, 39(3): 311-319. DOI:10.15918/j.tbit1001-0645.2019.03.014] |
| [10] |
Xu Yanhong,Shi Xiaowei,Xu Jingwei,et al. Range-angle-dependent beamforming of pulsed frequency diverse array[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(7): 3262-3267. DOI:10.1109/TAP.2015.2423698 |
| [11] |
Khan W,Qureshi I M. Frequency diverse array radar with time-dependent frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 758-761. DOI:10.1109/LAWP.2014.2315215 |
| [12] |
Yao Amin,Wu Wen,Fang Dagang. Frequency diverse array antenna using time-modulated optimized frequency offset to obtain time-invariant spatial fine focusing beampattern[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(10): 4434-4446. DOI:10.1109/TAP.2016.2594075 |
| [13] |
Wang Yuxi,Li Wei,Huang Guoce,et al. Time-invariant range-angle-dependent beampattern synthesis for FDA radar targets tracking[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2375-2379. DOI:10.1109/LAWP.2017.2718580 |
| [14] |
Liao Yi,Wang Wenqin,Zheng Zhi. Frequency diverse array beampattern synthesis using symmetrical logarithmic frequency offsets for target indication[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(5): 3505-3509. |
| [15] |
Shi Jiantao.On time-invariant FDA beam-pattern design based on time-dependent frequency offsets[C]//Proceedings of the 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop(SAM).Hangzhou:IEEE,2020:1–4.
|
| [16] |
Lan Lan,Liao Guisheng,Xu Jingwei,et al. Transceive beamforming with accurate nulling in FDA–MIMO radar for imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4145-4159. DOI:10.1109/TGRS.2019.2961324 |
| [17] |
Lan Lan,Xu Jingwei,Liao Guisheng,et al. Suppression of mainbeam deceptive jammer with FDA–MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11584-11598. DOI:10.1109/TVT.2020.3014689 |
| [18] |
Wang Yuzhuo,Zhu Shengqi. Main-beam range deceptive jamming suppression with simulated annealing FDA–MIMO radar[J]. IEEE Sensors Journal, 2020, 20(16): 9056-9070. DOI:10.1109/JSEN.2020.2982194 |
| [19] |
Xu Jingwei,Zhu Shengqi,Liao Guisheng. Range ambiguous clutter suppression for airborne FDA–STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1620-1631. DOI:10.1109/JSTSP.2015.2465353 |
| [20] |
Zhu Yu,Liu Lei,Lu Zheng,et al. Target detection performance analysis of FDA–MIMO radar[J]. IEEE Access, 2019, 7: 164276-164285. DOI:10.1109/ACCESS.2019.2943082 |
| [21] |
Liu Qi,Xu Jingwei,Ding Zhi,et al. Target localization with jammer removal using frequency diverse array[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11685-11696. DOI:10.1109/TVT.2020.3016948 |
| [22] |
Wang Wenqin,Chen Hui,Zheng Zhi,et al. Advances on frequency diverse array radar and its applications[J]. Journal of Radars, 2018, 7(2): 153-166. [王文钦,陈慧,郑植,等. 频控阵雷达技术及其应用研究进展[J]. 雷达学报, 2018, 7(2): 153-166. DOI:10.12000/JR18029] |
| [23] |
Cui Yanshuo.Research on frequency diverse array transmit beam control technology[D].Chengdu:University of Electronic Science and Technology of China,2019:6–14. 崔延硕.频控阵发射波束控制技术研究[D].成都:电子科技大学,2019:6–14. |
| [24] |
Wang Wenqin. Information geometry resolution optimization for frequency diverse array in DOA estimation[J]. Signal Processing, 2020, 169(6): 107376. DOI:10.1016/j.sigpro.2019.107376 |
| [25] |
Xu Yanhong,Luk K M. Enhanced transmit–receive beamforming for frequency diverse array[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(7): 5344-5352. DOI:10.1109/TAP.2020.2977717 |
 2021, Vol. 53
2021, Vol. 53


