2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116
2. State Key Lab. of Deep Geomechanics and Underground Eng., China Univ. of Mining and Technol., Xuzhou 221116, China
探索岩体中流体的流动机理对解决隧道开挖和地下工程施工过程中的突涌水问题具有重要意义[1]。工程扰动引起的应力、水压变化会改变裂隙内空腔的大小和几何形态,进而导致渗流特性的变化。这一变化在裂隙发生剪切错位时显得尤为突出[2]。在裂隙发育的富水岩体中,工程扰动容易使流体进入非线性流动状态,给渗流特性的精确评价带来困难[3]。因此,通过基础试验和数值模拟深入研究裂隙在弹性和弹塑性变形条件下的非线性渗流特性具有重要意义。
裂隙岩体一般包含有大量的单裂隙,研究单裂隙的变形与渗透特性是理解裂隙岩体水力耦合特性的先决条件。早期的研究将岩石裂隙简化为2个光滑的平行板,利用Navier–Stocks方程可推导出表示流量与开度之间关系的立方定律。实际的天然裂隙由粗糙表面组成,开度e在空间上不是一个恒定值。因此,大量学者利用力学开度em、等效水力开度eh及表征裂隙面粗糙特征的参数对立方定律进行修正[4],在一定程度上拓展了立方定律的适用范围。
对于单裂隙而言,施加于裂隙上的法向应力所引起的变形是影响裂隙过流能力的主要原因。众多学者对法向应力作用下粗糙岩石裂隙的变形和渗流特性进行了广泛的试验和理论研究。Wang等[5]研究表明,岩石在受正应力作用时,裂隙的闭合曲线为受裂隙表面特征控制的函数。Iwai[6]通过试验发现,裂隙面粗糙度对渗流特性的影响主要是通过改变其接触面积体现。Kranzz等[7]通过室内试验指出裂隙渗透系数与法向应力呈幂函数递减关系。张文泉等[8]根据采动过程中裂隙岩体的应力变化,探讨在恒定法向荷载和恒定法向刚度条件下裂隙岩体粗糙度和渗透水压对试样渗透系数的影响规律,发现粗糙度与岩体的刚度成反比,与水力开度最终稳定值成正相关。
影响岩石裂隙水力耦合特性的另一个重要因素是剪切过程。一方面,剪切错位造成裂隙内部接触状态变化,直接影响裂隙在法向应力作用下的变形特性;另一方面,剪切造成内部空腔结构变化,导致裂隙渗透系数及非线性渗流特性变化[9]。学者们通过剪切–渗流耦合试验,已初步掌握渗透系数在剪切过程中随剪胀的三段式演化规律[10]。通过求解Navier–Stocks(NS)方程,发现了表征非线性渗流的临界水力梯度和临界雷诺数在剪切过程中的演化特征[11]。结果表明,随着剪切位移的增大,法向位移不断增大,临界水力梯度和临界雷诺数均逐渐增大,且增大速率均为先增大后减少。
除了流体本身的性质之外,裂隙中的接触面和粗糙度,即裂隙内的空腔结构特征是导致非线性渗流的重要原因。流速较小时,流体一般为达西流,可以用达西定律计算裂隙的渗透系数;但随着流速的增大,裂隙两端的水头差与流量之间逐渐演变为非线性关系,这一转换受到裂隙内部空腔结构特征的控制。Bear[12]提出用Forchheimer定律表示该非线性关系,已得到大量试验和数值模拟结果的验证;该方程中的惯性系数B受到诸多因素的影响,难以定量确定,在实际工程应用中还存在较大困难。为此,Chen等[13]研究了可变形粗糙裂隙中围压对Forchheimer定律中系数A和B的影响;Zhou等[14]整理了大量室内和现场渗流试验结果和孔隙尺度渗流模型计算结果,定量分析了Forchheimer定律中的黏性渗透系数kv和惯性渗透系数ki,发现两种渗透系数存在ki=β·kv α/2的关系;Liu等[15]通过数值方法生成大量粗糙裂隙表面,并模拟了裂隙面剪切渗流过程,认为随着剪切的进行,系数A和B具有相同的变化规律,但系数B的数值比A的高约6个数量级;Zhang等[16]发现系数B随着微裂缝开度的增大而减小;Li[17]和Zhang[18]等都发现了当开度场固定时,增加剪切位移和粗糙度可以提高Forchheimer定律中二次项的比例。同一裂隙在不同剪切位移和受力环境下的几何形态不同,从而改变了裂隙交叉口的几何特征,Liu等[19]发现在复杂裂隙网络中的裂缝通道长度和宽度是影响比流体分流比的主要因素。
以往研究一般分别考虑法向应力、剪切过程和非线性渗流,尚未综合建立关键控制参数,例如应力、位移、开度、惯性系数等之间的关系,且相关模型也较少得到试验验证。为定量研究法向应力和剪切错位对裂隙非线性渗流特性的影响规律,针对含单裂隙花岗岩试样开展了应力–渗流耦合试验,基于自主开发的裂隙受压变形模拟程序计算裂隙变形,获取裂隙内部空腔几何数据;然后,利用COMSOL软件模拟裂隙内的渗流,分析同一裂隙在不同剪切错动条件下的变形破坏与非线性渗流特性,找出各控制参数之间的数学关系。
1 试验方法试验中主要采用了夹持器、TELEDYNE ISCO 柱塞泵、VR–3100 3D 轮廓测量仪、高精度差压计等仪器。柱塞泵的流量量程为0.001至200 mL/min,分辨率为0.001 mL/min;差压计的量程为10 Pa至100 kPa,分辨率为10 Pa。试验选取3个采自同一地点的花岗岩标准试样(G–1、G–2、G–3),直径均为50 mm,高度均为100 mm,将试样放置于具有楔形压头的万能试验机上,通过加压沿轴线劈裂制成裂隙,见图1。
 |
| 图1 花岗岩试样制备和裂隙表面形貌 Fig. 1 Preparation of granite samples and their surface morphology |
由于夹持器内部橡胶圈直径有限,表面起伏大的裂隙在错动后无法放置,所以试验选取裂隙表面起伏较小的试样(G–1)作为后期渗流试验的对象和数值对象,G–2和G–3扫描后作为数值模拟对象。为更精确地控制试样的剪切位移量,根据试样的几何特征,利用3D打印机打印了2、4、6、8 mm 4种厚度的高强度树脂垫片各2片。这些垫片底部设置了锯齿状结构,不影响水的流动;将垫片用胶水粘贴于试样端面后,为橡胶套提供支撑。
图2为水力耦合试验装置的示意图。如图2所示,将试样置于夹持器中,夹持器的入口端连接柱塞泵C和差压计入口端,出口端连接电子秤上的废液盒和差压计出口端;围压孔连接柱塞泵A,轴压孔连接柱塞泵B。另外,准备3个标准试样在MTS815试验机上开展单轴压缩试验,测得该种花岗岩的平均单轴抗压强度UCS=137.80 MPa,弹性模量E=41.20 GPa,泊松比ν=0.29。由于研究主要关注不同剪切错位下法向应力对渗透特性的影响效果,所以未采用直接剪切的形式,而是在一个剪切位移测试结束后取出试样,扫描表面;然后,人工错位到下一个剪切位移,再装入试样进行法向加载和渗流测试,以保证所有的表面损伤皆源自法向加载。
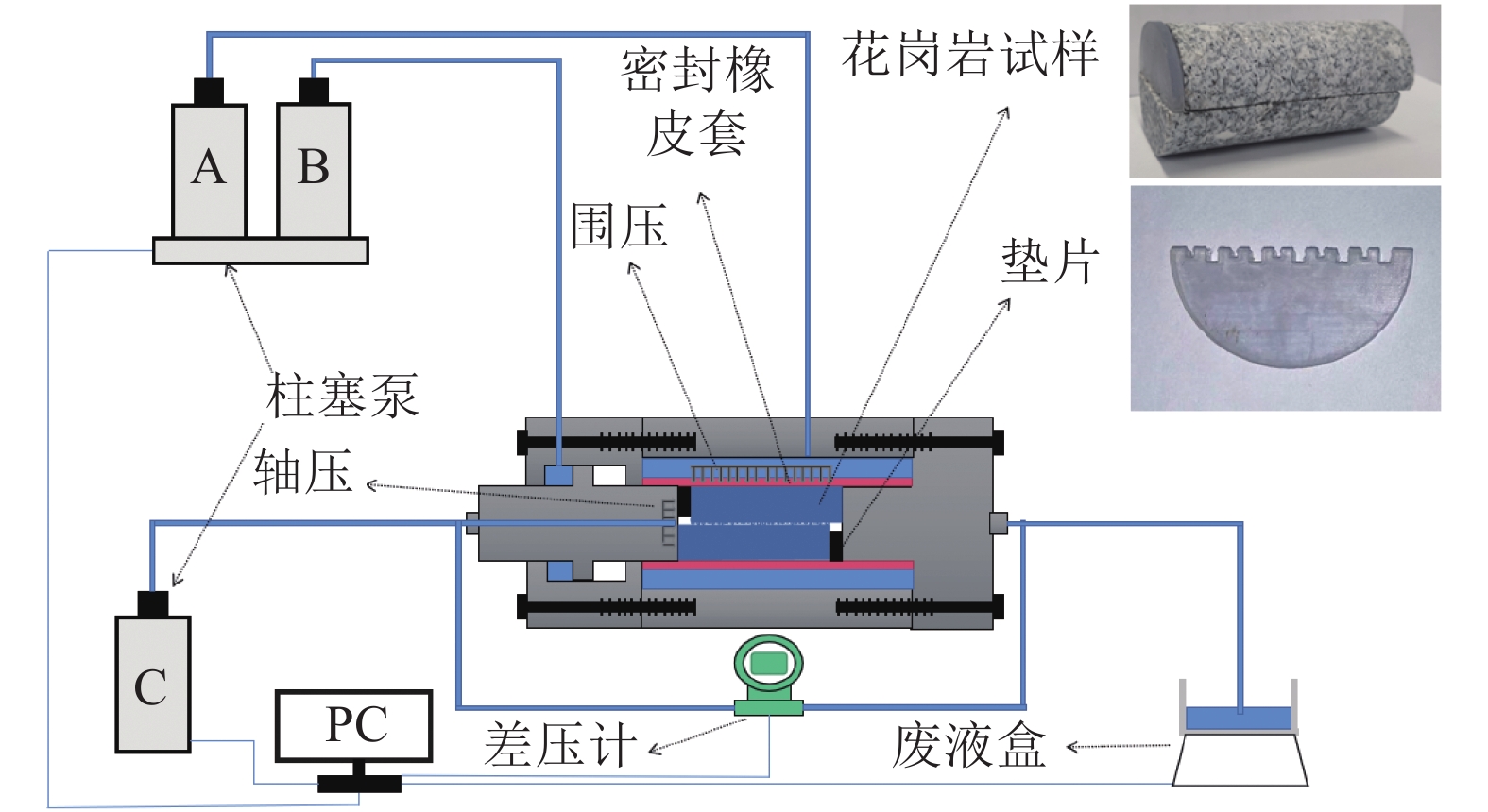 |
| 图2 水力耦合试验装置示意图 Fig. 2 Schematic diagram of the coupled stress-flow testing apparatus |
首先,在开始渗流试验前先施加0.50 MPa的围压和轴压,从而保证试样的密闭性;然后,缓慢注水以排出内部气体使各个导管与试样内部完全充满水;随后,关闭柱塞泵C,待差压计稳定显示为0后,对试样依次施加不同的法向应力,在每种应力下进行不同流速的渗流测试,并用计算机实时记录差压计的读数。体积流速范围为1.67×10–7至3.33×10–6 m3/s。首次进行渗流测试的法向应力为2 MPa,并按每次2 MPa不断增大。剪切位移变大后,试样悬空的部分易发生断裂破坏,为保证试样的完整性,在2、4、6、8 mm 4种剪切位移时施加的最大法向应力分别为10、8、8、6 MPa。在每个剪切位移测试结束后,将上下裂隙表面进行冲水清理,去除附着于裂隙面上的碎屑。使用VR–3100高精度3维轮廓仪(点间距分辨率为0.10 μm)扫描得到压缩试验后的3维裂隙表面,将测试前后的裂隙表面几何模型相减即可得到表面的破坏区域。
2 数值模拟方法 2.1 裂隙面的受压变形破坏数值模拟通过高精度轮廓仪扫描0(初始状态)、2、4、6、8 mm 5种剪切位移条件下的试样表面,并建立3维数值模型。考虑到整个试验过程使用的是同一个试样,每个剪切位移的法向加载测试后,裂隙表面都会发生一定的破坏并不断累积,所以下一个剪切位移的表面数值模型使用前一个位移试验后扫描所得的裂隙面作为原型。
以往相关研究中,通常将岩石假设为纯弹性体,裂隙的变形模拟一般通过刚性地移动裂隙2个表面计算接触体上的弹性变形来实现。事实上,裂隙表面凸体在受压过程中不仅会产生弹性变形,还可能发生破坏,所以在数值模拟计算过程中,应充分考虑到裂隙表面接触体的弹性变形和弹塑性变形破坏过程。裂隙中的流体在2个粗糙表面形成的复杂空腔结构中流动,变形计算的精度直接影响着模型内部空腔结构的建模精度。由于加压试验过程中试样无法取出,所以为同时获得裂隙面破坏情况和重现裂隙在夹持器内受压时的状态,进而实现不同受压状态下的裂隙渗流模拟,采用自行开发的基于接触力学变分原理框架[20]的受压变形计算程序解决这一问题。该方法以求解接触系统的最小势能为基础,将塑性变形引起的能量耗散添加到Tian和Bhushan提出的总互补势能公式中,得到以下的计算接触应力与裂隙变形之间的关系式[21]:
| $ \begin{aligned}[b] V_{}^* =& \frac{{\text{1}}}{{\text{2}}}\iint_\Omega {{\sigma _{\text{n}}}{{\overline u }_\textit{z}}(x,y){\text{d}}x{\text{d}}y} - \iint_\Omega {\sigma _{\text{n}}}\bigg[\overline u _\textit{z}^*(x,y)-\bigg. \\ & \bigg.\frac{{\text{1}}}{{\text{2}}}\Delta u_\textit{z}^p(x,y)\bigg]{\text{d}}x{\text{d}}y \\ \end{aligned} $ | (1) |
式中:
计算时,根据剪切位移量错动2个表面,设定岩石的力学参数E和υ,按照Δσn=0.10 MPa逐步加载,并记录法向位移和法向应力及每步加载中产生的塑形破坏量。根据裂隙表面的弹塑性计算结果可得到裂隙内部空腔的高精度几何数据。计算模型的点间距为0.20 mm,满足高精度受压变形计算的需要[21]。
2.2 裂隙渗流数值模拟COMSOL Multiphysics是一款以有限元为基础的多物理场耦合模拟仿真软件,广泛应用于岩石裂隙渗流计算,其有效性得到了充分的检验[22]。将受压变形计算得到的上、下裂隙面处理后以dxf.格式导入COMSOL中,随后在软件内建立裂隙空腔模型,如图3所示。
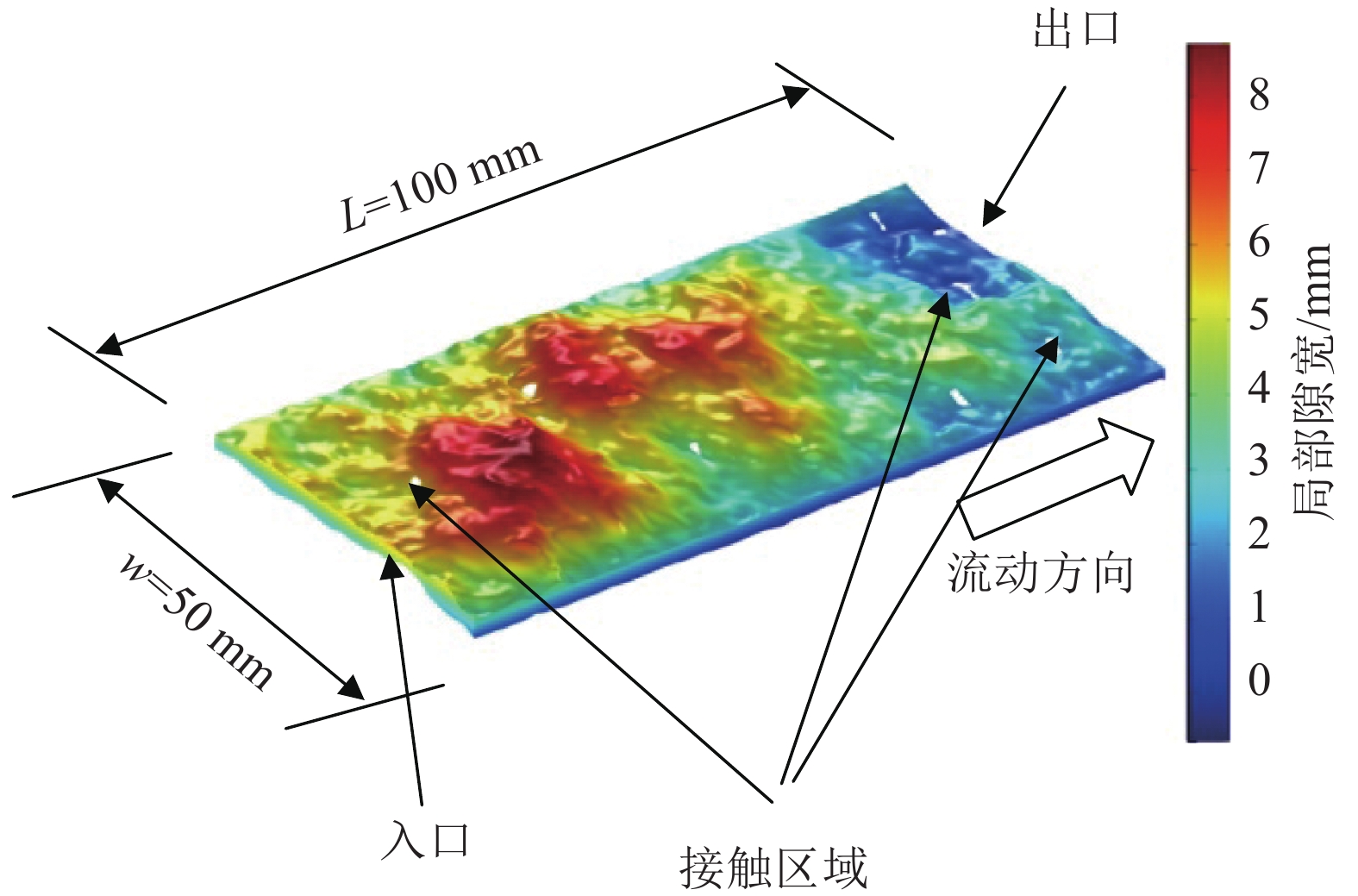 |
| 图3 裂隙空腔数值模型 Fig. 3 Numerical model of void spaces in a fracture |
模型长100 mm,宽50 mm,高度用颜色表示,在0~8 mm之间。通过求解COMSOL中的层流模块自带的NS方程获取裂隙内的3维流场分布。对于不可压缩牛顿流体,稳态流动由NS方程控制,可写成[22] :
| $ \rho \left[\frac{{\partial {\boldsymbol{u}}}}{{\partial t}} + ({\boldsymbol{u}} \cdot \nabla ){\boldsymbol{u}}\right] = \nabla \cdot {\boldsymbol{T}} + {\boldsymbol{f}}\rho - \nabla {\boldsymbol{P}} $ | (2) |
式中:u为流速矢量,m/s;t为时间,s ;P为压力矢量,Pa;ρ为流体的密度,kg/m3;T为剪应力矢量,Pa;f为体力矢量,m/s2。根据试验条件,设裂隙中的流体为等温、稳定的不可压缩牛顿流体,密度为999.70 kg/m3,动力黏度为1×10–3 N·s/m2。
本文采用COMSOL中的层流模块,用常规自由四面体对模型进行划分,由于裂隙面接触点处的几何形状复杂,因此,在这些位置进行适当的网络细化,以提高计算的精度。以剪切位移2 mm的模型为例,模型包含了1 841 775个单元,在i7内核的计算机上单次计算时长为9 h。入口边界条件定义为考虑流体惯性和定流量的“充分发展的流动”,体积流速范围设为10–8~4×10–5 m3/s,出口边界条件为“0 Pa”,即开放的边界。该范围相对于试验测试的范围更宽,便于充分考察线性和非线性渗流特征。对于不可压缩流体,针对非线性流动的Forchheimer方程和线性流动的渗透率计算公式[23]可以分别写为:
| $ \nabla P = AQ + B{Q^{\text{2}}} = \frac{\mu }{{{k_{\rm{v}}}}}\upsilon + \frac{\rho }{{{k_{\rm{i}}}}}{\upsilon ^{\text{2}}} $ | (3) |
| $ K = - \frac{{Q\mu }}{{S\nabla P}} $ | (4) |
式中:Q为入口流量,m3/s;A为线性项系数,Pa·s·m–4;B为非线性项的系数,也即惯性系数,Pa·s2·m–7;kv为黏性渗透率,m2;ki为惯性渗透率,m;υ为体积通量,m/s;μ为动力黏度,Pa·s;K为裂隙渗透率,m2;S为试样横截面面积,m2。
对于裂隙流,雷诺数Re可以定义为[24] :
| $ Re = \frac{{\rho Q}}{{w\mu }} $ | (5) |
式中,w为裂隙沿压力梯度方向的宽度,m。
3 试验和数值模拟结果分析 3.1 裂隙变形和破坏区域分析图4为裂隙力学开度em与法向应力σn、剪切位移量d的关系。
 |
| 图4 裂隙力学开度与法向应力、剪切位移量关系 Fig. 4 Relationships among fracture mechanical aperture, normal stress and shear displacement |
如图4(a)所示,随着裂隙面上所施加的法向应力的增加,力学开度非线性减小,具有式(6)所示的幂函数关系:
| $ {e_{\text{m}}} = a \times {\sigma^b _{\text{n}}} $ | (6) |
式中,a和b为系数。
系数a和b的值都随着剪切位移的增加而增加,这主要是由裂隙面上凸起部位的随机分布引起的。随着剪切位移d从2增加到8 mm,系数a由1.35增加到2.02,增加了90.45%;系数b由–0.11增加到–0.06,增加了45.45%。裂隙面错动后,接触面逐渐集中,在法向应力作用下发生破坏,导致上下表面逐渐接近,从而产生新的接触,增大裂隙的法向刚度。随着法向压力的增大,开度的变化速率减缓,裂隙的变形过程趋于稳定。
如图4(b)所示,随着剪切位移的增加,力学开度呈非线性关系增大,但增加速率逐渐降低,具有式(7)所示的对数函数关系:
| $ {e_{\text{m}}} = c\ln\; d + n $ | (7) |
式中,c和n为系数。
随着法向应力从2增加到10 MPa,系数c变化较小,稳定于0.51至0.53之间;系数n从0.92降低到0.69,降低了25%,其变化趋势和Bandis等[25]的试验结果一致。
为进一步探究裂隙开度和裂隙面接触位置的破坏形态,通过改变应力大小,对2、4、6、8 mm 4种剪切位移发生后的裂隙进行相应的数值模拟,并绘制裂隙在不同应力下的塑性破坏高程图,见图5(a)。随着剪切位移增大,法向位移也随之增大,上下表面的相关度降低,导致接触点个数和塑性破坏点数量减少。当保持恒定的剪切位移时,随着法向应力的增加,塑性破坏点位置不会发生显著的变化。2 MPa法向应力下所产生的塑性破坏区域多为尖状的微凸体,其面积随着法向应力的增加而增加,这进一步证实了图4(a)中应力–开度曲线逐渐趋于平缓的原因。
 |
| 图5 不同剪切位移下裂隙面塑性破坏演化规律 Fig. 5 Evolutions of plastic failure zones under different shear displacements |
图5(b)为扫描试样获取的不同剪切位移下裂隙塑性破坏高程图及相应的数值模拟结果,试验和数值模拟计算得到的塑性破坏空间位置分布吻合较好,但试验所得的破坏面积和高度略大于数值模拟结果。这主要是因为花岗岩属于脆性材料,由大量的矿物颗粒组成,部分颗粒的损坏会导致周边的颗粒随之脱落;数值计算过程仅将局部应力大于临界应力的接触面定义为破坏区域,忽略了对邻近岩石基质的影响。上述结果验证了裂隙弹塑性接触模型能够准确捕捉粗糙裂隙损伤行为,重现了裂隙表面的塑性破坏区域及其演化规律。
3.2 渗流特性分析图6为不同剪切位移条件下水力梯度和渗透率的关系。
 |
| 图6 不同剪切位移条件下水力梯度和渗透率的关系 Fig. 6 Relationships between hydraulic gradient and permeability under different shear displacement |
如图6所示:数值模拟得到的渗透率K随水力梯度J的变化规律和室内渗流试验结果基本一致,均呈现逐渐减少的变化趋势,且降低速率均先增大后减少。随着剪切位移的增加,接触点个数减少且开度增大,渗透率K也逐渐增大。试验得到的渗透率K略小于数值模拟得到的渗透率K,主要是因为在扫描的过程中会损失一部分精度,导致实际裂隙表面比扫描得到的表面更粗糙,同时错动过程也会带来一定的误差。
虽然应力和剪切位移会对渗透率和水力梯度曲线产生一定的影响,但总体变化趋势相同。在流速较小时,流体处于达西流动状态,裂隙岩体的渗透率K变化较小;当水力梯度J增加到一个临界值后,流体在惯性力作用下进入了非线性渗流阶段,渗透率K降低较快,且随着流速的继续增大,所有工况的K值都逐渐集中并趋于平缓。以d = 6 mm和σn = 10 MPa为例,裂隙在雷诺数Re为0.2、2.0、20.0和200.0时的流线分布如图7所示,入口均设置了200条流线。
 |
| 图7 不同雷诺数下裂隙内的流线分布 Fig. 7 Streamline distributions of fluid flow under different Re values |
由图7可知,随着Re的增加,出口流线数量减少,且流体所流经的区域也减少,这与流体惯性力的增大有关。流体在高流速情况下会绕开大开度裂隙附近的部分小裂隙,而且更易被裂隙的接触和突起等几何结构变化所扰动,导致数值模拟中流线的不连续和数量减少的现象。随着剪切位移的增大,接触点个数减少,但单个接触点面积增大,流体集中在若干优势流动通道中,对裂隙渗流能力起主要控制作用。
为解决流体流动的非线性,定义非线性因子Nf[26]为:
| $ {N_{\text{f}}} = \frac{{B{Q^{\text{2}}}}}{{AQ + B{Q^{\text{2}}}}} $ | (8) |
该方程量化了非线性分量在总量中的比例,且被广泛接受。当Nf=0.1时,流体流动从线性状态过渡到非线性状态,临界点相应的水力梯度定义为临界水力梯度Jc。
Forchheimer方程作为描述裂隙中流体非线性流动特性的方程,惯性系数B与非线性渗流特性密切相关,将法向应力σn和剪切位移d对临界水力梯度Jc和惯性系数B的影响均做了分析,如图8所示。
 |
| 图8 临界水力梯度和惯性系数随剪切位移的变化规律 Fig. 8 Evolutions of the critical hydraulic gradientsand the coefficients under different shear displacement |
由图8可知:随着剪切位移的增大,临界水力梯度Jc和惯性系数B均呈幂函数关系逐渐减少,减少速率逐渐降低。随着法向应力的增大,Jc和B均逐渐增大。当法向应力在2到10 MPa范围内变化时,随着剪切位移的增大,Jc和B的波动范围均急剧减少。例如:当剪切位移从2增加到8 mm时,Jc的波动范围从2.07×10–2–1.46×10–2=6.10×10–3减少到4.90×10–3–3.70×10–3=1.20×10–3,降低了80.32%;B的波动范围从4.63×1014–1.66×1014=2.97×1014 Pa·s2·m–7减少到7.09×1013–4.66×1013=2.43×1013 Pa·s2·m–7,降低了91.28%。
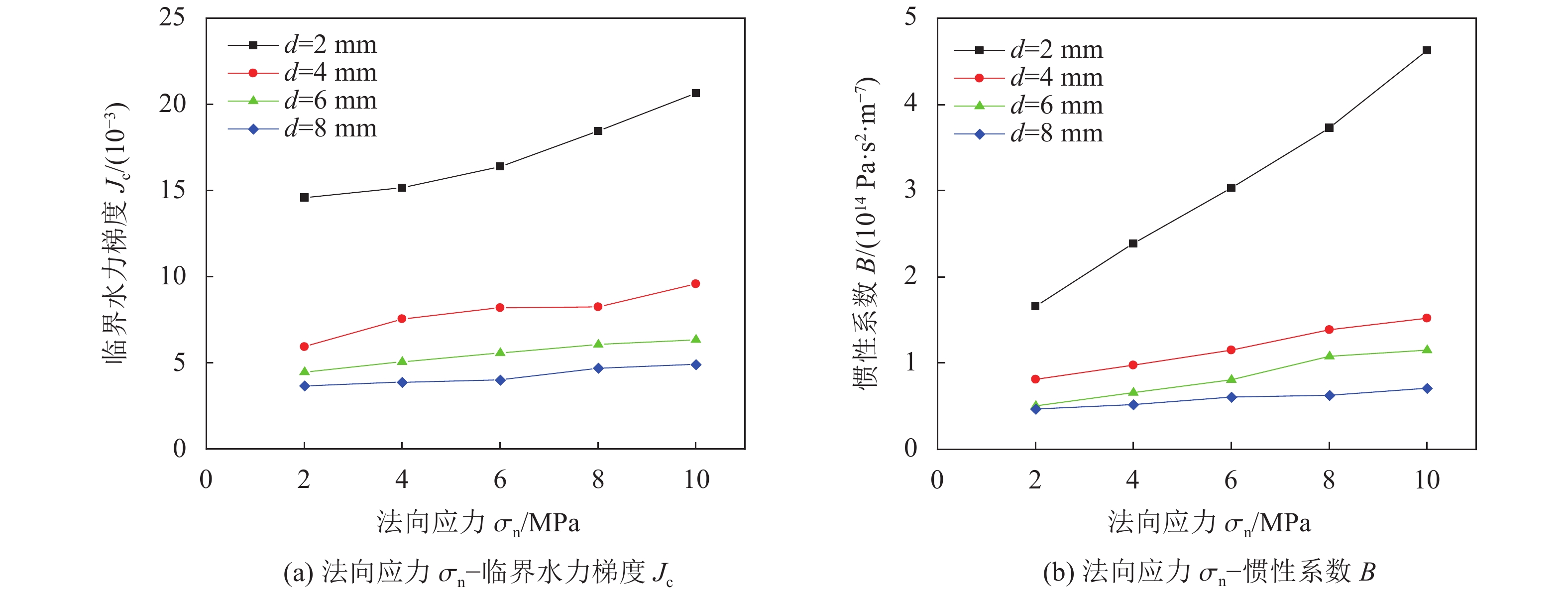
当剪切位移保持恒定时,增加法向应力会导致裂隙面的接触区域增加,进而使得裂隙内部的几何更加复杂,流体的路径也随之复杂化,增强了裂隙内渗流的非线性能力。如图9所示,随着法向应力的增加,Jc和B均呈近似线性的上升趋势,且随着剪切位移的增大,Jc和B的增加速率逐渐降低。
 |
|
图9 临界水力梯度和惯性系数随法向应力的变化规律 Fig. 9 Evolutions of the critical hydraulic gradients |
例如:当剪切位移从2增加到4 mm时,临界水力梯度Jc的增加速率从7.58×10–4降低到4.58×10–4 MPa–1,减少了39.58%;惯性系数B的增加速率从3.71×1013降低到8.84×1012 Pa·s2·m–7·MPa–1,减少了76.17%。当剪切位移从4增加到8 mm时,临界水力梯度Jc的增加速率从4.58×10–4降低到0.16×10–4 MPa–1,减少了65.94%;惯性系数B的增加速率从8.84×1012降低到3.04×1012 Pa·s2·m–7·MPa–1,减少了65.60%。结果表明,剪切位移越小,相同应力作用下裂隙开度越小,Jc和B对法向应力越敏感。
相对标准偏差(RSD)是刻画裂隙内开度分布特征的常用指标,定义为局部开度的标准偏差除以平均开度。通过数据拟合,建立裂隙内部几何特征与非线性渗流控制参数(Jc和B)的关系,结果如图10所示,其中,U为剪切位移与裂隙面总长度之比(即剪切应变)。
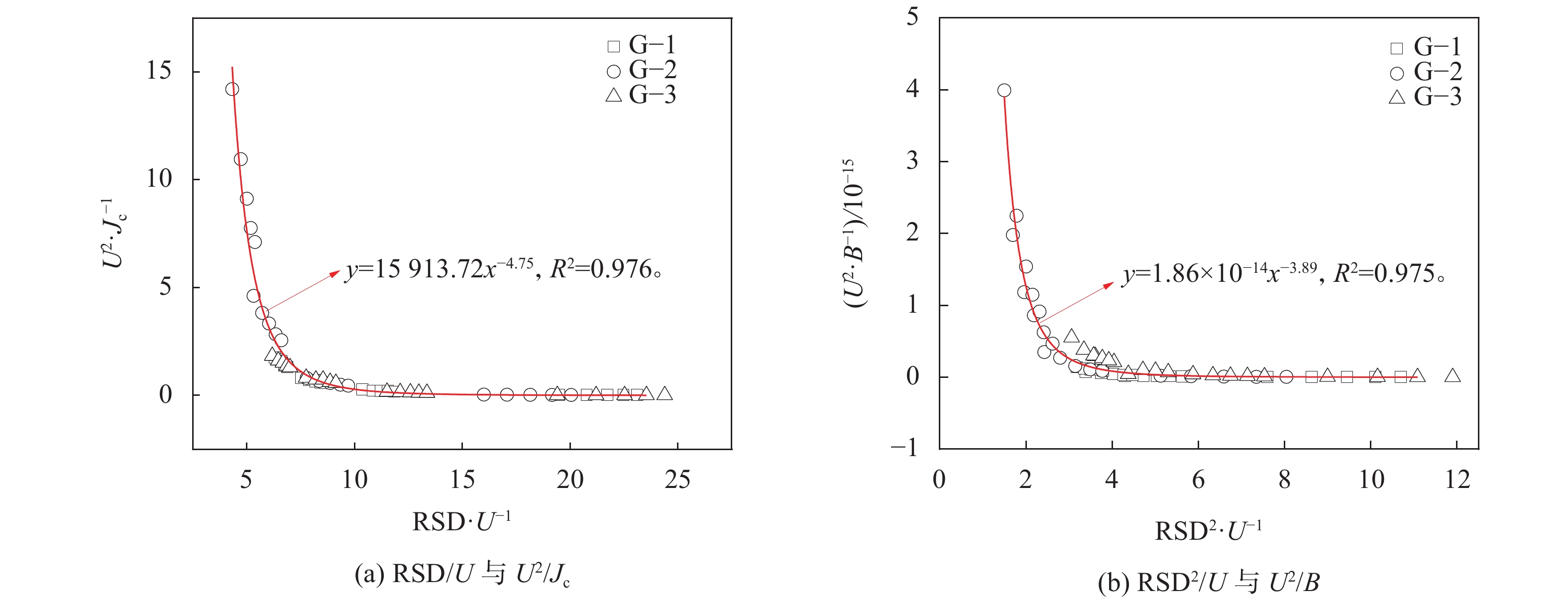 |
| 图10 临界水力梯度Jc和惯性系数B和裂隙几何参数RSD、U的数据拟合结果 Fig. 10 Data fitting results for critical hydraulic gradient Jc, inertia coefficient B and fracture geometric parameters RSD and U |
由图10可知:Jc和B 与RSD之间都存在类似的幂函数关系。这一结果表明,应力和位移是影响裂隙渗流特性的外因,内部空腔的几何特征是控制非线性渗流的首要因素,其中,剪切位移可造成空腔形态的显著变化,是一个不可忽略的因素。图10中包含了G–1、G–2、G–3这3个试样的数值计算结果,得到的规律具有普适性。在实际应用中,可通过统计裂隙开度分布特征,基于图10中的拟合公式计算裂隙的非线性渗流控制参数。
4 结 论通过试验和数值模拟的相互验证,建立了一套评价法向应力和剪切错位条件下裂隙非线性渗流特性的有效方法。力学方面,通过对应力、位移及裂隙表面形貌的高精度测试及数值计算,精确获取了裂隙的宏观变形行为及细观接触破坏规律,从而建立了裂隙内部空腔结构的3维高精度模型;渗流方面,通过对水压、流速的精确测控加上精细化3维数值模拟,定量描述了裂隙力学、几何参数与非线性渗流控制参数之间的关系,揭示了压剪作用下裂隙内部渗流场的演化规律。主要结论如下:
1)裂隙力学开度em和法向应力σn呈幂函数关系em=aσn b,随着剪切位移d从2增加到8 mm,系数a由1.35增加到2.02,系数b由–0.11增加到–0.06。裂隙力学开度em和剪切位移d呈对数函数关系em=cln d+n,随着法向应力σn从2增加到10 MPa,系数c变化较小,稳定于0.51至0.53之间,系数n从0.92降低到0.69。
2)在线性流动区域内,渗透率不受水力梯度J的影响,保持恒定的常数;但在非线性流动区域内,随着水力梯度J的增加,渗透率依次经历了缓慢降低、急剧降低和缓慢降低的过程。渗流试验结果和数值模拟结果吻合良好,证明了该数值模拟技术的可靠性。
3)随着剪切位移的增大,区分线性流动和非线性流动的临界水力梯度Jc和惯性系数B的波动范围均急剧减小。例如,当剪切位移从2增加到8 mm时,Jc降低了80.32%,B降低了91.28%。
4)随着法向应力增加,Jc和B均呈近似线性的上升趋势,且随着剪切位移增大,Jc和B的增加速率逐渐降低。如:当剪切位移从2增加到4 mm时,Jc的增加速率减少了39.58%,B的增加速率减少了76.17%。当剪切位移从4增加到8 mm时,Jc的增加速率减少了65.94%,B的增加速率减少了65.60%。结果表明,剪切位移越小,裂隙开度越小,Jc和B对法向应力越敏感。
5)临界水力梯度Jc和惯性项系数B与裂隙空腔几何特征参数RSD之间存在幂函数关系,且受到剪切应变U的影响,所建立的方程可为裂隙内非线性渗流特性评价提供定量的参考。
目前的研究尚未考虑实际岩体中裂隙长度、空间分布、岩石种类等的影响。这些因素对裂隙渗流具有重要作用,需要在今后的工作中逐渐完善。
| [1] |
Zhou Zongqing,Li Liping,Shi Shaoshuai,et al. Study on tunnel water inrush mechanism and simulation of seepage failure process[J]. Rock and Soil Mechanics, 2020, 41(11): 3621-3631. [周宗青,李利平,石少帅,等. 隧道突涌水机制与渗透破坏灾变过程模拟研究[J]. 岩土力学, 2020, 41(11): 3621-3631. DOI:10.16285/j.rsm.2020.0131] |
| [2] |
Zou L,Jing L,Cvetkovic V. Shear-enhanced nonlinear flow in rough-walled rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 97: 33-45. DOI:10.1016/j.ijrmms.2017.06.001 |
| [3] |
Wang M,Chen Y,Ma G,et al. Influence of surface roughness on nonlinear flow behaviors in 3D self-affine rough fractures:Lattice Boltzmann simulations[J]. Advances in Water Resources, 2016, 96: 373-388. DOI:10.1016/j.advwatres.2016.08.006 |
| [4] |
Xie L Z,Gao C,Ren L,et al. Numerical investigation of geometrical and hydraulic properties in a single rock fracture during shear displacement with the Navier–Stokes equations[J]. Environmental Earth Sciences, 2015, 73(11): 7061-7074. DOI:10.1007/s12665-015-4256-3 |
| [5] |
Wang L,Cardenas M. Development of an empirical model relating permeability and specific stiffness for rough fractures from numerical deformation experiments[J]. Journal of Geophysical Research(Solid Earth), 2016, 121(7): 4977-4989. DOI:10.1002/2016JB013004 |
| [6] |
Iwai K.Fundamental studies of fluid flow through a single fracture[D].Berkeley:University of California, 1976:54–60.
|
| [7] |
Kranzz R L,Frankel A D,Engelder T,et al. The permeability of whole and jointed Barre Granite[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(4): 225-234. DOI:10.1016/0148-9062(79)91197-5 |
| [8] |
Zhang Wenquan,Yuan Jiudang,Wang Zhongchang,et al. An experimental study on compressive shear seepage laws of mining-induced fractured rock mass[J]. Rock and Soil Mechanics, 2017, 38(9): 2473-2479. [张文泉,袁久党,王忠昶,等. 采动裂隙岩体压剪渗透规律试验研究[J]. 岩土力学, 2017, 38(9): 2473-2479. DOI:10.16285/j.rsm.2017.09.002] |
| [9] |
Li B,Jiang Y,Koyama T,et al. Experimental study of the hydro-mechanical behavior of rock joints using a parallel-plate model containing contact areas and artificial fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(3): 362-375. DOI:10.1016/j.ijrmms.2007.06.004 |
| [10] |
Xiong X,Li B,Jiang Y,et al. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1292-1302. DOI:10.1016/j.ijrmms.2011.09.009 |
| [11] |
Liu R,Li B,Jiang Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks:The roles of aperture,surface roughness,and number of intersections[J]. Advances in Water Resources, 2016, 88: 53-65. DOI:10.1016/j.advwatres.2015.12.002 |
| [12] |
Bear J.Dynamics of fluids in porous media[M].New York:Elsevier,1972:177–182.
|
| [13] |
Chen Y,Zhou J,Hu S,et al. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015, 529: 993-1006. DOI:10.1016/j.jhydrol.2015.09.021 |
| [14] |
Zhou J,Chen Y,Wang L,et al. Universal relationship between viscous and inertial permeability of geologic porous media[J]. Geophysical Research Letters, 2019, 46(3): 1441-1448. DOI:10.1029/2018GL081413 |
| [15] |
Liu R,Huang N,Jiang Y,et al. A numerical study of shear-induced evolutions of geometric and hydraulic properties of self-affine rough-walled rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 127: 104211. DOI:10.1016/j.ijrmms.2020.104211 |
| [16] |
Zhang S,Qiao W,Wu Y,et al.Experimental study on seepage characteristics of microfracture with different aperture[J].Scientific Reports,2020,10:5452.
|
| [17] |
Li J,Li X,Zhang B,et al. Effect of lower surface roughness on nonlinear hydraulic properties of fractures[J]. Geofluids, 2021, 2021: 1-9. DOI:10.1155/2021/6612378 |
| [18] |
Zhang Y,Chai J,Cao C,et al. Combined influences of shear displacement,roughness,and pressure gradient on nonlinear flow in self-affine fractures[J]. Journal of Petroleum Science and Engineering, 2021, 198: 108229. DOI:10.1016/j.petrol.2020.108229 |
| [19] |
Liu Chunting,Li Mingzhong,Zhang Guodong. Numerical investigation of fluid flow in fracture junctions with consideration to effect of fracture morphology[J]. Energy Science & Engineering, 2021, 9(8): 1289-1300. DOI:10.1002/ese3.868 |
| [20] |
Bhushan B. Contact mechanics of rough surfaces in tribology:Multiple asperity contact[J]. Tribology Letters, 1998, 4(1): 1-35. DOI:10.1023/A:1019186601445 |
| [21] |
Zou L,Li B,Mo Y,et al. A high-resolution contact analysis of rough-walled crystalline rock fractures subject to normal stress[J]. Rock Mechanics and Rock Engineering, 2020, 53(4): 2141-2155. DOI:10.1007/s00603-019-02034-w |
| [22] |
Cardenas M B,Slottke D T,Ketcham R A,et al. Navier–Stokes flow and transport simulations using real fractures shows heavy tailing due to eddies[J]. Geophysical Research Letters, 2007, 34(14): L14404. DOI:10.1029/2007GL030545 |
| [23] |
Liu R,Jiang Y,Li B,et al. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks[J]. Computers and Geotechnics, 2015, 65: 45-55. DOI:10.1016/j.compgeo.2014.11.004 |
| [24] |
Zimmerman R W,Bodvarsson G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media, 1996, 23(1): 1-30. DOI:10.1007/BF00145263 |
| [25] |
Bandis S C,Lumsden A C,Barton N R.Fundamentals of rock joint deformation[J].International Journal of Rock Mechanics and Mining Sciences,1983,20(6):249–268.
|
| [26] |
Javadi M,Sharifzadeh M,Shahriar K,et al. Critical Reynolds number for nonlinear flow through rough-walled fractures:The role of shear processes[J]. Water Resources Research, 2014, 50(2): 1789-1804. DOI:10.1002/2013WR014610 |
 2021, Vol. 53
2021, Vol. 53


