2. 公安部特勤局,北京 100850
2. Security and Protection Dept. of Public Security Ministry, Beijing 100850, China
螺纹连接是工程结构中最常用的紧固方式之一,作为连接部件,螺栓螺母的紧固能力关系着包括被连接件在内整个结构的安全性与可靠性[1−3]。其松动脱落等力学问题一直是国内外相关学者研究重点之一[4−6]。目前对螺纹连接力学性能及松动机理的研究方法主要有实验检测、理论分析和数值计算。
在对螺纹结构进行实验检测时,由于螺纹加工精度和表面粗糙度不同,导致实验结果较为分散,实验重复性差[7−8]。
随着计算机技术的发展,国内外学者运用有限元法对螺纹连接结构的性能进行了广泛研究,并取得了一定成果。在用有限元法分析螺纹连接的力学行为时,由于螺纹升角结构复杂,难以划分优质的有限元网格。为了简化计算,许多研究人员通常假定有限元模型的螺纹部分具有轴对称几何特性或直接忽略模型的螺纹结构。如:Verwaerde等[9]采用3维实体单元模型对螺栓连接结构进行了有限元分析,虽然在一定程度上表征了螺纹连接结构上的应力分布,但模型忽略了连接处的螺纹,无法反映螺纹连接处的真实应力分布。Noda等[10]利用轴对称模型进行螺栓连接结构的应力分析,得到了相对满意的结果,但轴对称模型虽然考虑了螺纹的作用,却忽略了螺纹升角对结果的影响。
使用带升角结构的精确螺纹有限元模型开展数值计算,是准确预测螺纹处3维应力分布的有效方法,但由于工业生产中实际的需求不同,使用到的螺栓螺母紧固件种类繁多。因此,在进行有限元数值仿真计算时,如果需要针对不同型号的螺纹结构进行有限元数值研究,建立模型和网格划分将耗费大量精力,同时将出现网格质量难以保证、数值计算不易收敛、仿真成本高等问题[11−13]。故寻找一种计算结果准确、建模便捷的螺纹紧固件有限元建模方法具有十分重要的意义。
本文采用ISO给定的标准螺旋线公式建立垂直于螺纹中心轴线的螺纹螺旋线几何形状,以此螺纹螺旋线几何形状为基本几何,将其分别沿螺纹径向和轴向,顺次构建等比例缩放和固定角度旋转的平面螺纹螺旋线相似几何;然后,将单个节距螺纹上所得到的全部螺旋线等间距离散成若干节点,并将这些离散节点按位置关系组合成精度较高的3维8节点(C3D8)单元,即获得单个节距螺纹3维有限元模型;再将此单个节距的模型,沿螺纹中心轴线堆叠适当个数,得到多节距的螺纹连接结构3维有限元模型(该建模具体实施过程可查阅文献[14])。最后,通过数值算例对建立的模型进行了验证,并在Qt框架下开发螺栓螺母有限元参数化建模平台,为实际工程提供了更为科学的支撑和更高效的设计工具。
1 有限元模型本文螺纹轮廓线的规格由文献[15]给出,为了防止螺纹齿根处发生过度的应力集中现象,要求齿根半径不得小于0.125
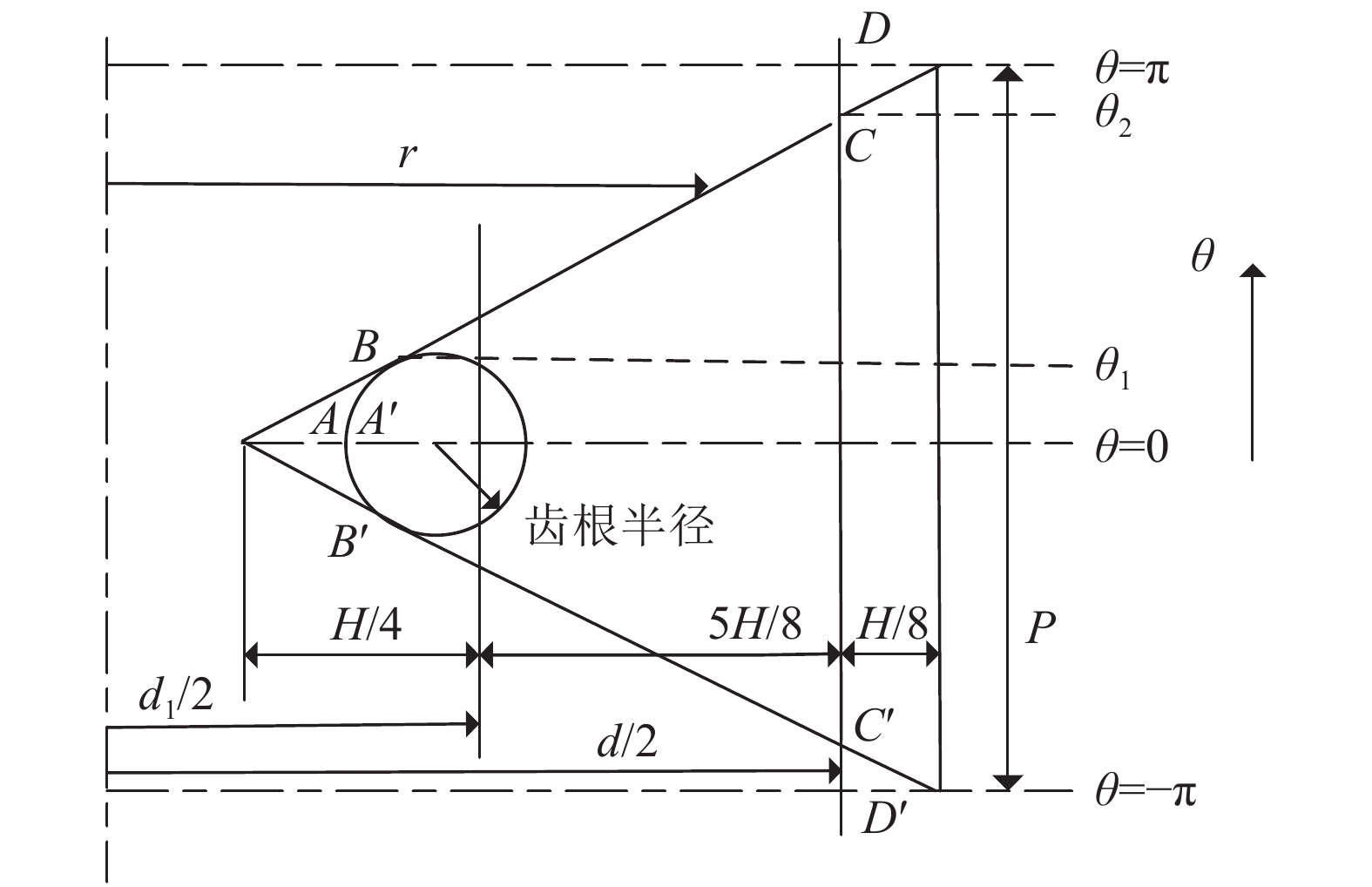 |
| 图1 沿螺栓中心轴线的螺纹截面 Fig. 1 Thread section along the central axis of the bolt |
将这3部分的轮廓线延展成绕螺栓轴线的平面,投影到垂直于螺栓轴的平面上,可得外螺纹轮廓线,如图2所示。
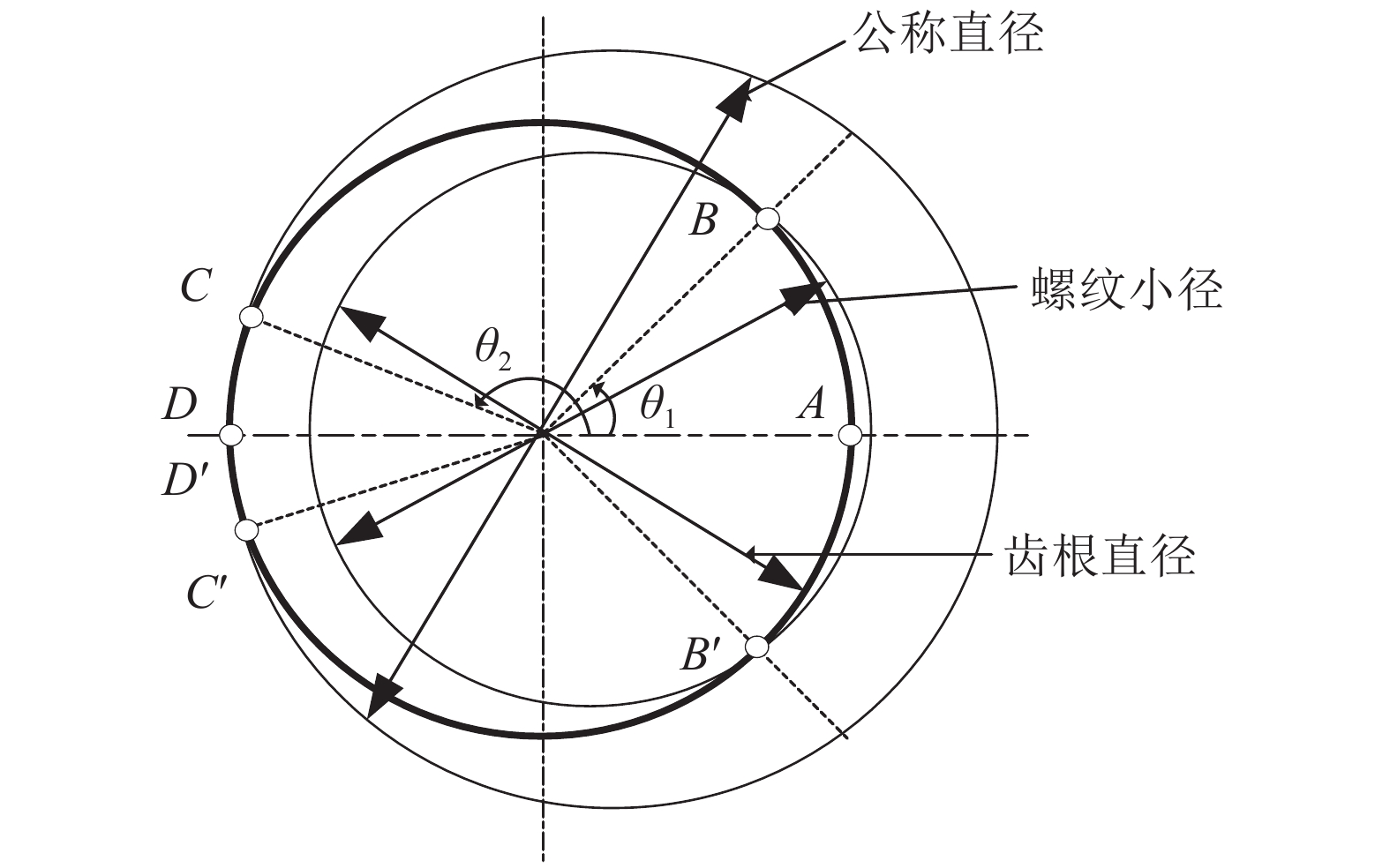 |
| 图2 外螺纹轮廓线示意图 Fig. 2 Sketch diagram of external thread profile |
此轮廓线轨迹
| $ {r_1} = \left\{ \begin{array}{l} \dfrac{d}{2} - \dfrac{7}{8}H + 2\rho - \sqrt {{\rho ^2} - \dfrac{{{P^2}}}{{4{\text{π} ^2}}}{\theta ^2}} {\text{ }},0 \le \theta \le {\theta _1} ; \\ \dfrac{H}{\text{π} }\theta + \dfrac{d}{2} - \dfrac{7}{8}H{\text{ }},{\theta _1} \le \theta \le {\theta _2} ; \\ \dfrac{d}{2}{\text{ }},{\theta _2} \le \theta \le \text{π} \end{array} \right. $ | (1) |
式中:
同样地,可获得螺母的内螺纹轮廓线轨迹
| $ {r_2} = \left\{ \begin{array}{l} \dfrac{{{d_1}}}{2},0 \le \theta \le {\theta _1} ;\\ \dfrac{H}{\text{π} }\theta + \dfrac{d}{2} - \dfrac{7}{8}H,{\theta _1} \le \theta \le {\theta _2} ;\\ \dfrac{d}{2} + \dfrac{1}{8}H - 2{\rho _{\text{n}}}{\text{ + }} \hfill \\ \quad \sqrt {{\rho _{\text{n}}}^2 - \dfrac{{{P^2}}}{{4{\text{π} ^2}}}{{(\text{π} - \theta )}^2}} ,{\text{ }}{\theta _2} \le \theta \le \text{π} \hfill \\ \end{array} \right. $ | (2) |
式中:
为了实现对不同型号螺纹连接结构有限元模型的便捷调用,在Qt平台上,利用OpenGL图形库开发了模型建立软件,软件界面如图3所示。
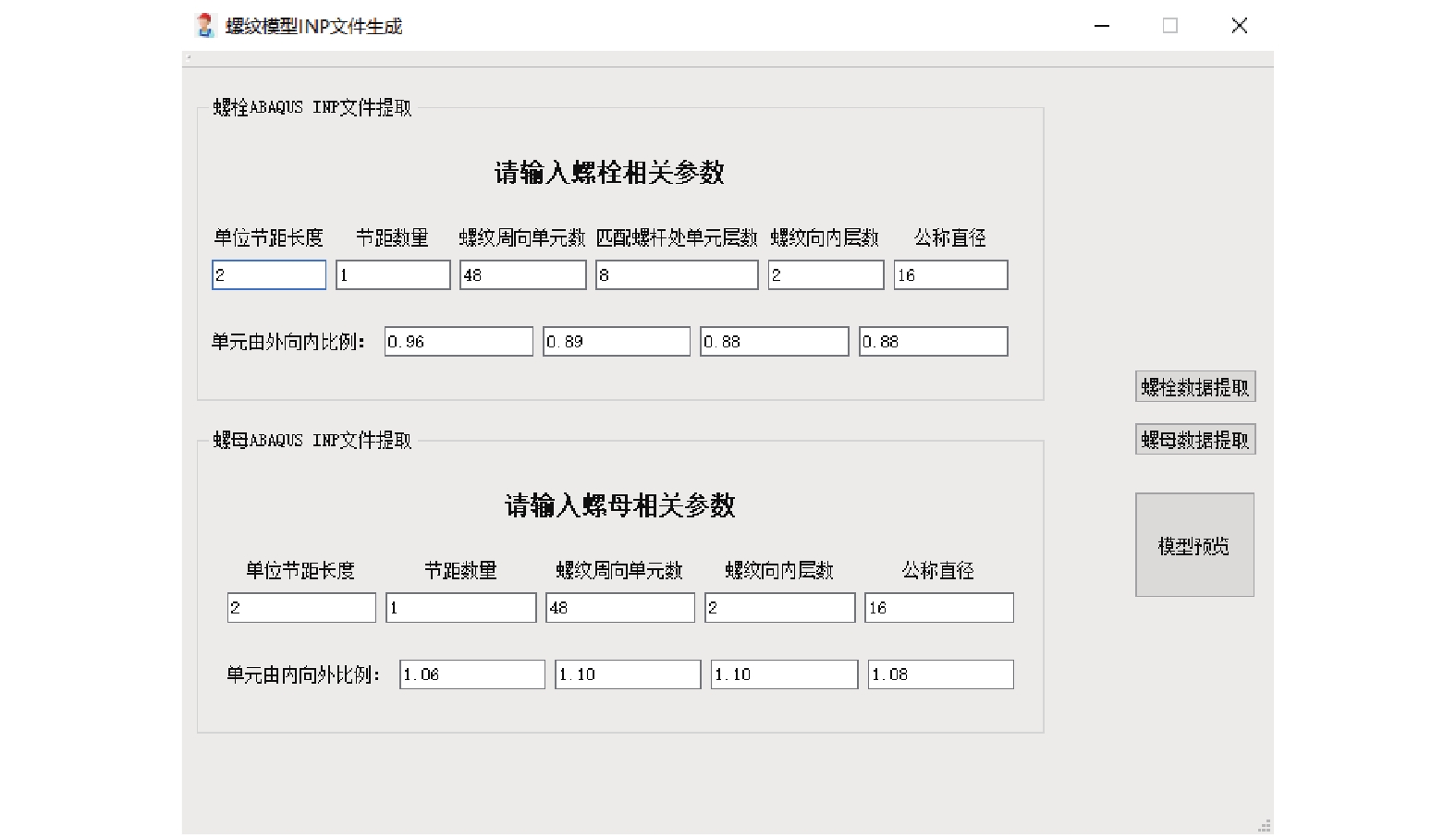 |
| 图3 建模软件界面 Fig. 3 Interface of modeling software |
图4为单位节距长度
 |
| 图4 不同公称直径的螺纹有限元模型 Fig. 4 Finite element models of screw threads with different nominal diameters |
2 螺纹连接中的力学关系
螺纹连接结构拧紧和受载时,力学行为的变化是一个强烈的状态非线性过程,该过程通常伴有复杂的几何非线性(大位移)和材料非线性(塑性)影响;螺纹连接结构处于不同状态时,其力学行为有着明显的差别。为便于计算分析,采用下述假定:
1)螺纹结构体的材料是连续均匀且完全弹性的;
2)作用在螺纹连接结构上的位移和形变是微小的,且结构体内无初始应力;
3)摩擦系数在整个运动受力过程中不发生变化,系统能量守恒。
2.1 螺栓轴向力与拧紧转角关系从螺纹的几何特征入手,当螺母绕螺栓转动时,螺母的轴向位移量
| $ s = P\vartheta /2\text{π} $ | (3) |
式中,
| $ {\delta _{\rm{b}}} = P\vartheta /(2\text{π}) $ | (4) |
然而,实际上,被连接件不可能刚性约束螺母的位移,所以在转动螺母,螺母发生位移的同时,螺栓也被拉长,螺栓和被连接件两者被拉长的占比,取决于二者刚度
| $ F = {K_{\rm{s}}}P\vartheta /2\text{π} {\text{ }} = {K_{\rm{b}}}{K_{\rm{j}}}P\vartheta /[2\text{π} ({K_{\rm{b}}} + {K_{\rm{j}}})] $ | (5) |
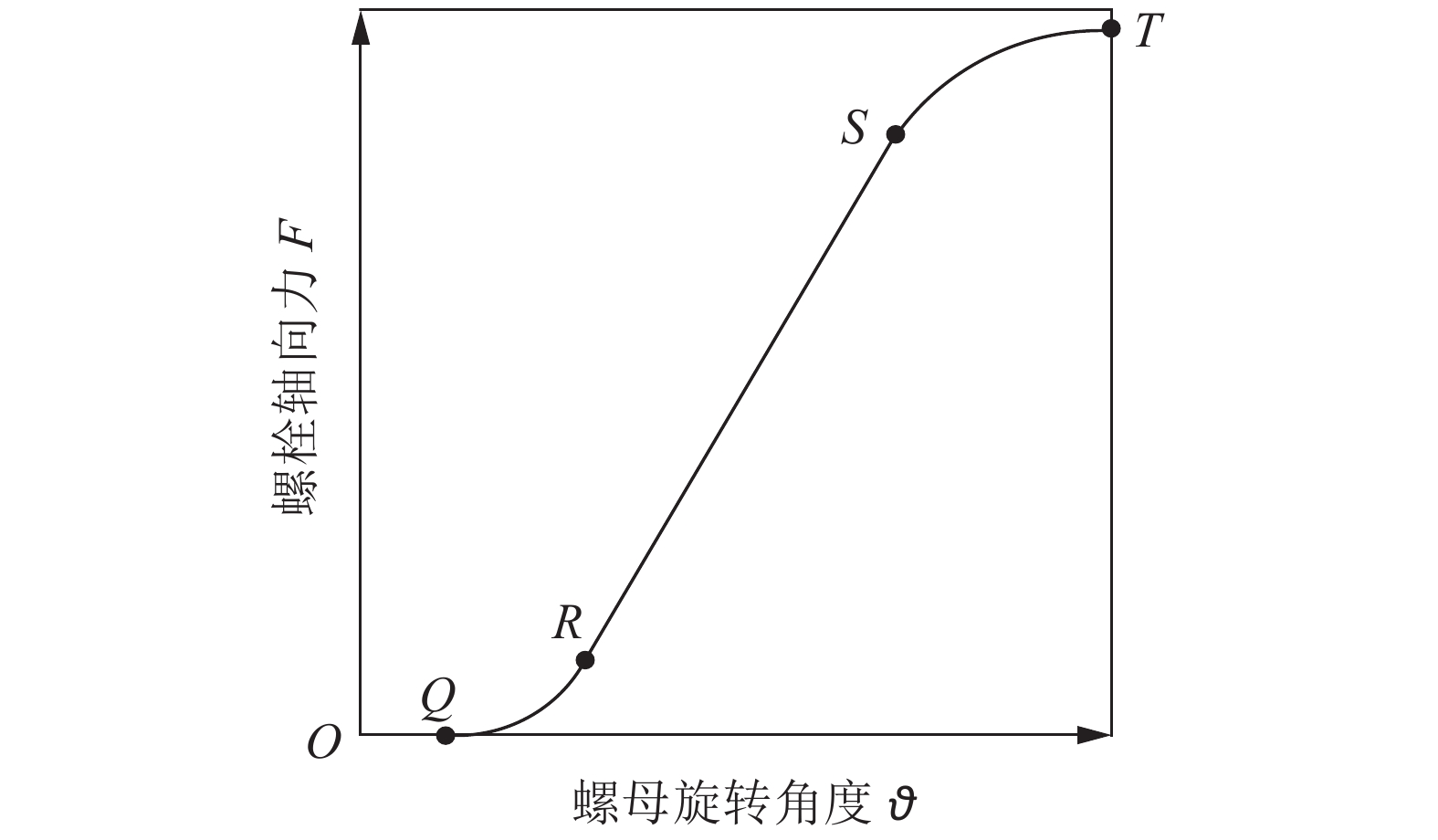
实际拧紧一个螺母时,在螺母和被连接件未发生接触的旋转期间,螺栓上不会产生轴向力。一旦螺母接触被连接件后,即会产生轴向力,由于表面接触区域面积较小或被连接件与周围构件的摩擦力影响等原因,轴向力起初会很小,但后期增长很迅速,这个过程称为被连接件的贴紧过程。贴紧过程要转多少角度无法预知,即使使用同种型号的螺栓和被连接件,贴紧过程中螺母转动的角度也会不一样[16]。被连接件贴紧后,从式(5)可知轴向力
 |
|
图5 轴向力
|
2.2 螺纹牙的轴向力分布推导
图6为旋和螺纹部分的轴向力F示意图,其中,
 |
|
图6 旋合螺纹部分的轴向力
|
| $ \left\{ {\begin{array}{l} {{\varepsilon _{\rm{b}}} = \displaystyle\int_0^x {\dfrac{F}{{{A_{\rm{b}}} \cdot {E_{\rm{b}}}}}} {\rm{d}}x}, \\ {{\varepsilon _{\rm{n}}} = \displaystyle\int_0^x {\dfrac{F}{{{A_{\rm{n}}} \cdot {E_{\rm{n}}}}}} {\rm{d}}x} \end{array}} \right. $ | (6) |
式中,
设作用于
| $ p\cos \;\alpha \cdot {\rm{d}}x\cot\; \varphi = {\rm{d}}F $ | (7) |
式中,
| $ p\cos \;\alpha = \frac{{{\rm{d}}F}}{{{\rm{d}}x}}\tan \;\varphi $ | (8) |
图7描述了由各种原因产生的螺纹牙变形。如图7(a)所示:对牙宽为
 |
| 图7 各种原因产生的螺纹牙变形 Fig. 7 Deformation of thread teeth for various reasons |
把上述所求得的变形分量相互累加,即获得外螺纹和内螺纹变形的总量
| $ \left\{ {\begin{array}{l} {{\delta _{\rm{b}}} = {\delta _{1{\rm{b}}}} + {\delta _{2{\rm{b}}}} + {\delta _{3{\rm{b}}}} + {\delta _{4{\rm{b}}}} + {\delta _{5{\rm{b}}}} = \dfrac{{{k_{\rm{b}}}}}{{{E_{\rm{b}}}}}p\cos\;\alpha}, \\ {{\delta _{\rm{n}}} = {\delta _{1{\rm{n}}}} + {\delta _{2{\rm{n}}}} + {\delta _{3{\rm{n}}}} + {\delta _{4{\rm{n}}}} + {\delta _{5{\rm{n}}}} = \dfrac{{{k_{\rm{n}}}}}{{{E_{\rm{n}}}}}p\cos\;\alpha} \end{array}} \right. $ | (9) |
式中,
将式(8)代入式(9),得:
| $ \left\{ {\begin{array}{l} {{\delta _{\rm{b}}} = \dfrac{{{k_{\rm{b}}}}}{{{E_{\rm{b}}}}} \cdot \tan\;\varphi \dfrac{{{\rm{d}}F}}{{{\rm{d}}x}}}, \\ {{\delta _{\rm{n}}} = \dfrac{{{k_{\rm{n}}}}}{{{E_{\rm{n}}}}} \cdot \tan\;\varphi \dfrac{{{\rm{d}}F}}{{{\rm{d}}x}}} \end{array}} \right. $ | (10) |
取图6中
| $ {({\varepsilon _{\rm{b}}} + {\varepsilon _{\rm{n}}})_{x = x}} = {({\delta _{\rm{b}}} + {\delta _{\rm{n}}})_{x = x}} - {({\delta _{\rm{b}}} + {\delta _{\rm{n}}})_{x = 0}} $ | (11) |
把式(7)和(10)代入式(11),并对
| $ \frac{{{{\rm{d}}^2}F}}{{{\rm{d}}{x^2}}} = {\lambda ^2}F $ | (12) |
式(12)中:
| $ \lambda = \sqrt {\dfrac{{\dfrac{1}{{{A_{\rm{b}}}{E_{\rm{b}}}}} + \dfrac{1}{{{A_{\rm{n}}}{E_{\rm{n}}}}}}}{{\left(\dfrac{{{k_{\rm{b}}}}}{{{E_{\rm{b}}}}} + \dfrac{{{k_{\rm{n}}}}}{{{E_{\rm{n}}}}}\right)\tan\; \varphi }}} = \sqrt {\dfrac{{\dfrac{1}{{{A_{\rm{b}}}}} + \dfrac{{{E_{\rm{b}}}}}{{{E_{\rm{n}}}}}\dfrac{1}{{{A_{\rm{n}}}}}}}{{\left({k_{\rm{b}}} + \dfrac{{{E_{\rm{b}}}}}{{{E_{\rm{n}}}}}{k_{\rm{n}}}\right)\tan\; \varphi }}} $ | (13) |
式(12)的通解为:
| $ F = {c_1}\cosh (\lambda x) + {c_2}\sinh (\lambda x) $ | (14) |
将边界条件
| $ \left\{ {\begin{array}{l} {{c_1}\cosh \;0 + {c_2}\sinh \;0 = 0}, \\ {{c_1}\cosh (\lambda L) + {c_2}\sinh (\lambda L) = {F_{\rm{b}}}} \end{array}} \right. $ | (15) |
式中,
双曲正弦和双曲余弦的函数式为:
| $ \left\{ \begin{array}{l} \sinh \;x = \dfrac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{2}, \\ \cosh \;x = \dfrac{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}}{2} \end{array} \right. $ | (16) |
联立式(15)与(16)可得:
| $ \left\{ \begin{array}{l} {c_1} = 0,\\ {c_2} = \dfrac{{{F_{\rm{b}}}}}{{\sinh (\lambda L)}} \end{array} \right. $ | (17) |
将
| $ \frac{F}{{{F_{\rm{b}}}}} = \frac{{\sinh (\lambda x)}}{{\sinh (\lambda L)}} $ | (18) |
将式(18)代入式(8)可得:
| $ p\cos \;\alpha = \lambda \frac{{\cosh (\lambda x)}}{{\sinh (\lambda L)}} \cdot {F_{\rm{b}}}\tan\; \varphi $ | (19) |
第
| $ \begin{aligned}[b] F_i =& \int_{(i - 1)P}^{iP} {p\cos \;\alpha \cot \;\varphi {\rm{d}}x} =\\& \int_{(i - 1)P}^{iP} {\lambda \frac{{\cosh (\lambda x)}}{{\sinh (\lambda L)}}{F_{\rm{b}}}{\rm{d}}x},i = 1,2,3, \cdots, L/P \end{aligned}$ | (20) |
定义
| $ {\eta _i} = \frac{{F_i}}{{{F_{\rm{b}}}}} = \left. {\frac{{\sinh (\lambda x)}}{{\sinh (\lambda L)}}} \right|_{(i - 1)P}^{iP} $ | (21) |
式(21)表明,对于螺纹结构式连接,轴向力在旋合各圈螺纹牙间所占比例满足双曲正弦函数关系,其轴向载荷比例分布如图8所示。
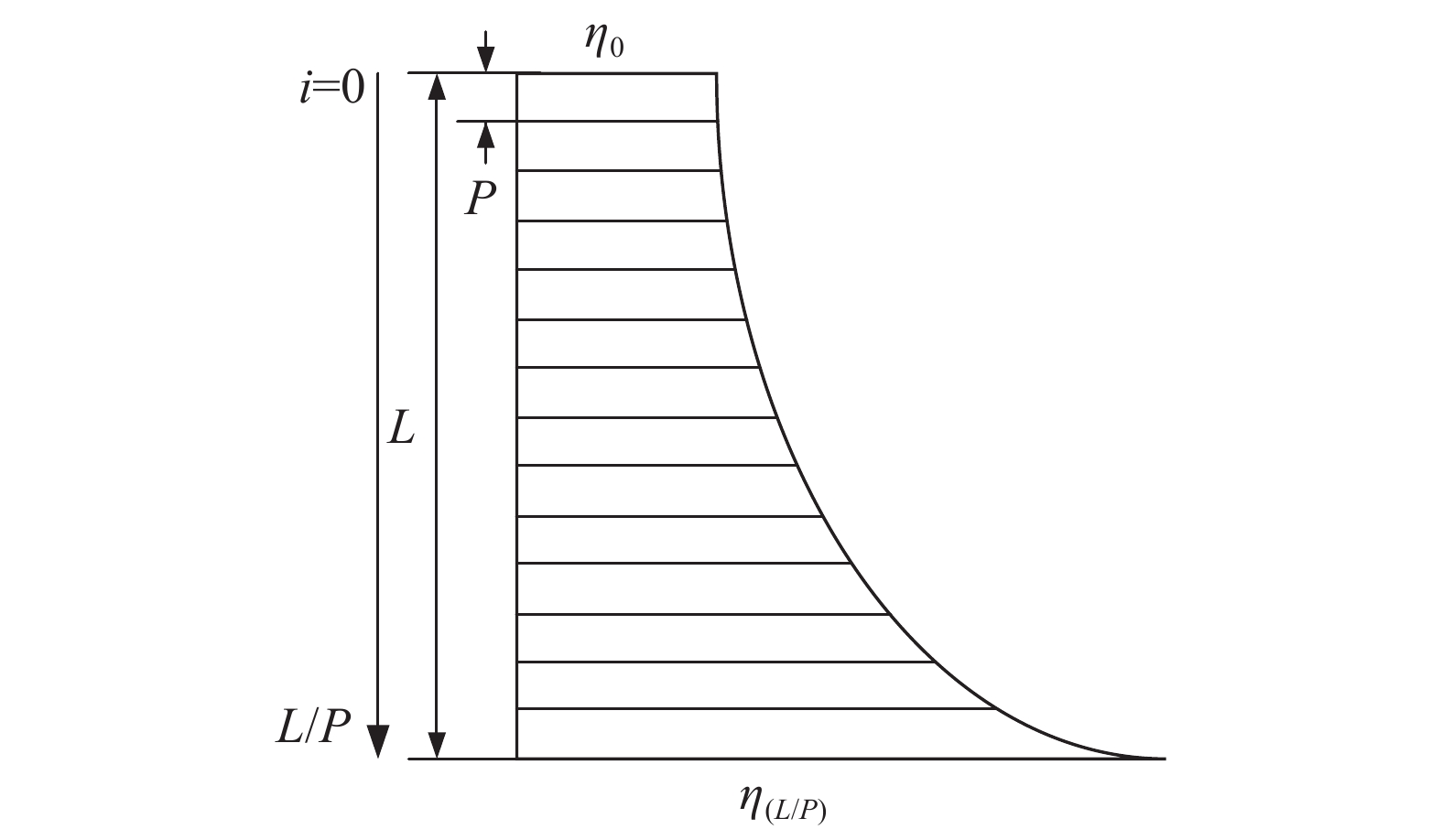 |
| 图8 轴向载荷比例分布示意图 Fig. 8 Diagram of axial load distribution |
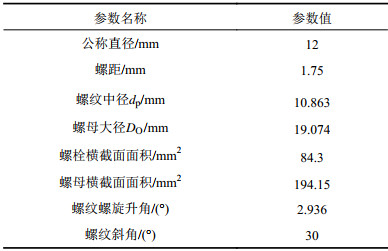
以M12标准螺栓螺母为研究对象,对螺栓轴向力分布进行计算。螺纹的几何参数见表1,螺栓、螺母弹性材料参数见表2,塑性应变行为见表3。
| 表1 M12螺纹的几何参数 Tab. 1 Geometric parameters of the M12 bolt |
 |
| 表2 螺栓螺母材料参数 Tab. 2 Material parameters of bolts and nuts |
 |
| 表3 螺栓螺母塑性应变行为 Tab. 3 Plastic strain behavior of bolts and nuts |
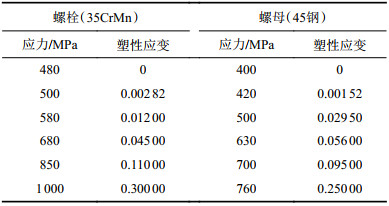 |
根据表2:取螺栓材料35CrMn,其弹性模量
| $ \left\{ {\begin{array}{l} {{\delta _{1{\rm{b}}}} = 0.034\left(\dfrac{{1 - {\nu _{\rm{b}}}^2}}{{{E_{\rm{b}}}}}\right)p\cos \;\alpha = 0.031\;22\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha}, \\ {{\delta _{2{\rm{b}}}} = 1.08\left(\dfrac{{1 + {\nu _{\rm{b}}}}}{{{E_{\rm{b}}}}}\right)p\cos \;\alpha = 1.388\;88\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha}, \\ {{\delta _{3{\rm{b}}}} = 0.229\left(\dfrac{{1 - {\nu _{\rm{b}}}^2}}{{{E_{\rm{b}}}}}\right)p\cos \;\alpha = 0.210\;27\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha}, \\ {{\delta _{4{\rm{b}}}} = 1.18\left(\dfrac{{1 - {\nu _{\rm{b}}}^2}}{{{E_{\rm{b}}}}}\right)p\cos \;\alpha = 1.083\;48\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha}, \\ {\delta _{5{\rm{b}}}} = {u_{\rm{b}}}\tan \;\alpha = (1 - {v_{\rm{b}}})\dfrac{{{{\tan }^2}\alpha}}{2} \cdot \dfrac{{{d_{\rm{p}}}}}{P} \cdot \dfrac{{p\cos \;\alpha}}{{{E_{\rm{b}}}}} {\text{ }} = \\\qquad\; 0.738\;68\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha \end{array}} \right. $ | (22) |
同样地,可求得内螺纹螺母的变形分量分别为:
| $ \left\{ {\begin{array}{l} {{\delta _{1{\rm{n}}}} = 0.073\left(\dfrac{{1 - {\nu _{\rm{n}}}^2}}{{{E_{\rm{n}}}}}\right)p\cos \;\alpha = 0.067\;72\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha}, \\ {{\delta _{2{\rm{n}}}} = 1.15\left(\dfrac{{1 + {\nu _{\rm{n}}}}}{{{E_{\rm{n}}}}}\right)p\cos \;\alpha = 1.459\;35\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha}, \\ {{\delta _{3{\rm{n}}}} = 0.294\left(\dfrac{{1 - {\nu _{\rm{n}}}^2}}{{{E_{\rm{n}}}}}\right)p\cos \;\alpha = 0.272\;73\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha} ,\\ {{\delta _{4{\rm{n}}}} = 1.14\left(\dfrac{{1 - {\nu _{\rm{n}}}^2}}{{{E_{\rm{n}}}}}\right)p\cos \;\alpha = 1.057\;51\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha}, \\ {\delta _{5{\rm{n}}}} = {u_{\rm{n}}}\tan\;\alpha = \left(\dfrac{{{D_{\rm{O}}}^2 + {d_{\rm{p}}}^2}}{{{D_{\rm{O}}}^2 - {d_{\rm{p}}}^2}} + {\nu _{\rm{n}}}\right)\dfrac{{{{\tan }^2}\alpha}}{2} \cdot \dfrac{{{d_{\rm{p}}}}}{P} \cdot \dfrac{{p\cos \;\alpha}}{{{E_{\rm{n}}}}} = \\ \qquad\; 2.306\;20\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha \end{array}} \right. $ | (23) |
将式(22)和(23)代入式(9),得:
| $ \left\{ {\begin{array}{l} {\delta _{\rm{b}}} = {\delta _{1{\rm{b}}}} + {\delta _{2{\rm{b}}}} + {\delta _{3{\rm{b}}}} + {\delta _{4{\rm{b}}}} + {\delta _{5{\rm{b}}}}= \\ \qquad \dfrac{{{k_{\rm{b}}}}}{{{E_{\rm{b}}}}}p\cos \;\alpha = 3.452\;53\dfrac{p}{{{E_{\rm{b}}}}}\cos \;\alpha, \hfill \\ {\delta _{\rm{n}}} = {\delta _{1{\rm{n}}}} + {\delta _{2{\rm{n}}}} + {\delta _{3{\rm{n}}}} + {\delta _{4{\rm{n}}}} + {\delta _{5{\rm{n}}}} = \\ \qquad \dfrac{{{k_{\rm{n}}}}}{{{E_{\rm{n}}}}}p\cos \;\alpha = 5.163\;51\dfrac{p}{{{E_{\rm{n}}}}}\cos \;\alpha \end{array}} \right. $ | (24) |
由式(24)可得,
| $ \begin{gathered} \lambda = \sqrt {\dfrac{{\dfrac{1}{{{A_{\rm{b}}}{E_{\rm{b}}}}} + \dfrac{1}{{{A_{\rm{n}}}{E_{\rm{n}}}}}}}{{\left(\dfrac{{{k_{\rm{b}}}}}{{{E_{\rm{b}}}}} + \dfrac{{{k_{\rm{n}}}}}{{{E_{\rm{n}}}}}\right)\tan\; \varphi }}} = \sqrt {\dfrac{{\dfrac{1}{{{A_{\rm{b}}}}} + \dfrac{{{E_{\rm{b}}}}}{{{E_{\rm{n}}}}}\dfrac{1}{{{A_{\rm{n}}}}}}}{{\left({k_{\rm{b}}} + \dfrac{{{E_{\rm{b}}}}}{{{E_{\rm{n}}}}}{k_{\rm{n}}}\right)\tan \;\varphi }}} {\text{ }} = 0.196\;11 \end{gathered} $ | (25) |
取螺母节距个数为6,单位长度为1.75 mm,则螺母总高度L=10.5 mm。因此,将以上结果代入式(18)和(21),可以获得第
| 表4 每圈螺纹上的载荷分布 Tab. 4 Load distribution on each thread |
 |
图9展示了沿螺母轴线向下,第
 |
| 图9 普通M12螺栓上轴向力的分布 Fig. 9 Distribution of axial forces on the normal M12 bolt |
由图9看出,第1圈承受了约30.2%的轴向力,第2圈承受了约21.9%的轴向力,前3圈螺纹约承受全部轴向力的68.3%。
3 有效性验证选用性能等级为5.8的M12粗牙标准螺纹紧固件有限元模型,在商业有限元计算软件ABAQUS中进行数值计算,将数值结果与第2节理论计算结果和以往工程实验结果进行对比分析,验证该螺纹连接结构有限元建模方法的有效性。
建立的整体模型结构如图10所示,共包含上层板、下层板、螺母和螺栓4个部件。这些部件全部采用C3D8R单元划分,模型共计节点87245个,单元77712个。
 |
| 图10 螺纹连接结构整体有限元模型 Fig. 10 Overall finite element model of screw joint structure |
在部件接触界面之间定义以下4组接触副:螺栓头部下表面和上层板的上表面之间(Cont1)、上层板的下表面和下层板的上表面之间(Cont2)、下层板的下表面和螺母的上表面之间(Cont3)、螺栓外螺纹表面和螺母内螺纹表面之间(Cont4),将以上4组接触副全部定义为表面与表面约束(standard)。接触行为设为切向和法向,其中,螺栓与螺母表面法向行为设为Exponential软接触约束,其余接触表面的法向行为设为硬接触约束。切向行为均采用罚公式接触约束。通过在螺母外部加载扭转载荷,使螺母向上转动从而夹紧两块形状相同的板材。模型中螺栓、螺母为弹塑性材料,板为弹性材料。各部件弹性材料参数见表2,螺栓、螺母塑性应变行为见表3。
针对本模型,在ABAQUS中进行如下求解设置。建立静力通用分析步,加载时间为1 s。最大增量步数设为100,初始增量步为0.01,模型考虑受几何非线性的影响。场输出变量选择应力、应变等。对于螺栓轴向力加载,ABAQUS中提供了一种模拟螺栓轴向力的加载方式,即在螺栓截面上施加螺栓载荷(bolt load)。这种加载方式将导致在下一分析步做扭转激励加载时,螺栓轴向力始终维持螺栓载荷所施加的荷载值而不发生变化。显然这与实际情况并不相符。因此,本文提出在螺母外侧施加旋转角度,以此模拟螺栓的预紧过程。图11中分别为ABAQUS中螺栓载荷加载方式与本文提到的扭转螺母加载方式在扭转激励作用下轴向力随时间的变化曲线。对比两条曲线发现:1) 由于螺栓载荷忽略了螺栓在预紧过程所受到的摩擦力矩和部件间实际接触状态,预紧过程呈线性增长,与工程实际中螺栓预紧情况不符。2) 在1~2 s阶段的扭转激励作用下,螺栓载荷加载方式使得轴向力维持不变,无法真实反映轴向力随扭转载荷变化的机理。因此,本文选用更加贴近实际工程的扭转螺母加载方式来完成螺栓轴向力的加载。
 |
| 图11 不同预紧方式下轴向力随时间的变化曲线 Fig. 11 Axial force versus time in different preloading modes |
3.1 拧紧转角和轴向力关系验证
在初始分析步(Step 0)中,对模型(图10)施加如下边界条件:在上层板上表面施加6个自由度的固定约束,下层板x方向侧面施加除z方向平移外的5个自由度固定约束,螺栓头部仅对绕z旋转的方向施加固定约束。
在维持初始分析步不变的前提下,在分析步(Step 1)中,对螺母施加0.3 rad转角,使结构处于拧紧状态。
在以上边界条件下,拧紧转角与轴向力的数值计算结果如图12所示,可以看到,拧紧转角和轴向力之间存在非线性关系。由于起初受被连接件与周围构件的摩擦力影响等原因,轴向力会很小,但轴向力的增长很迅速。当继续转动螺母,螺栓继续按比例伸长,此时,拧紧转角和轴向力呈线性关系。当达到材料的屈服点后,在同样的转角增量下,螺栓伸长量的增量增大,轴向力增量减小,轴向力
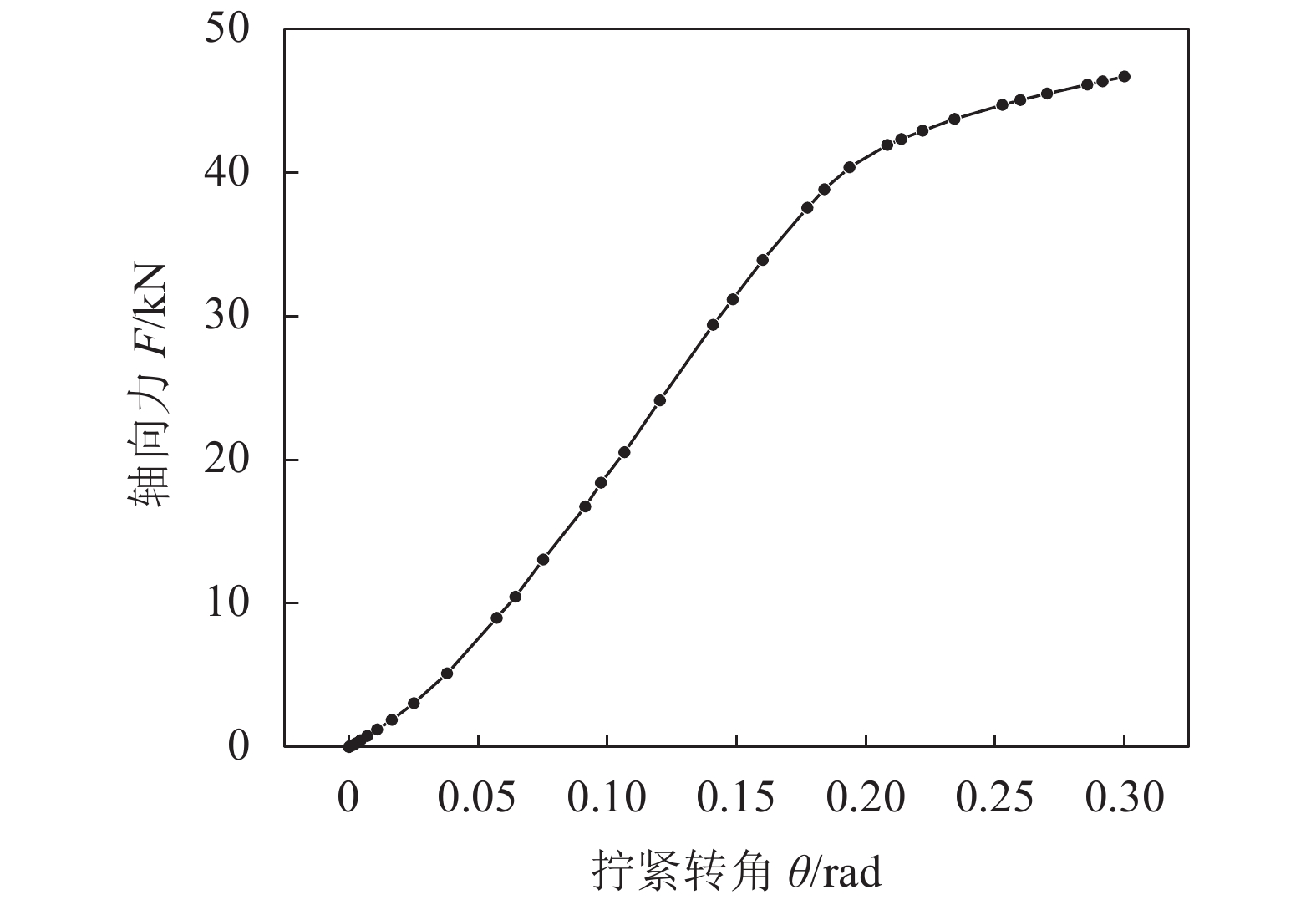 |
| 图12 轴向力随转角的变化曲线 Fig. 12 Curves of axial preloading force changing with the angle of rotation |
3.2 轴向力分布验证
为重现第2.2节中推导的无摩擦模型[17]在弹性理论下螺栓的轴向力分布结果,在不改变模型接触定义的情况下,将部件间的摩擦系数全设为0,并将图10中所有部件的塑性行为全部移除,其弹性材料参数见表2;对于性能等级为5.8的M12螺栓按照文献[18]中的轴向力施加标准,不改变第3.1节Step 0中设置的初始边界条件,在Step 1中对螺母重新进行扭转预紧,使螺栓获得螺栓轴向力20 kN,得到M12螺栓轴向力分布Mises应力云图(判断共用节点是否平均取值的变量变化梯度限定值为75%,下文同),如图13所示。
 |
| 图13 M12螺栓表面应力云图 Fig. 13 Stress contour of M12 bolt surface |
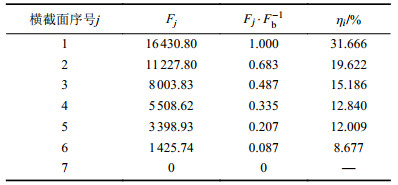
在ABAQUS中创建自由体切片,获得图13中横截面序号1~7指向的各截面j的截面轴向力
| 表5 各横截面受力分布 Tab. 5 Force distribution on each cross section |
 |
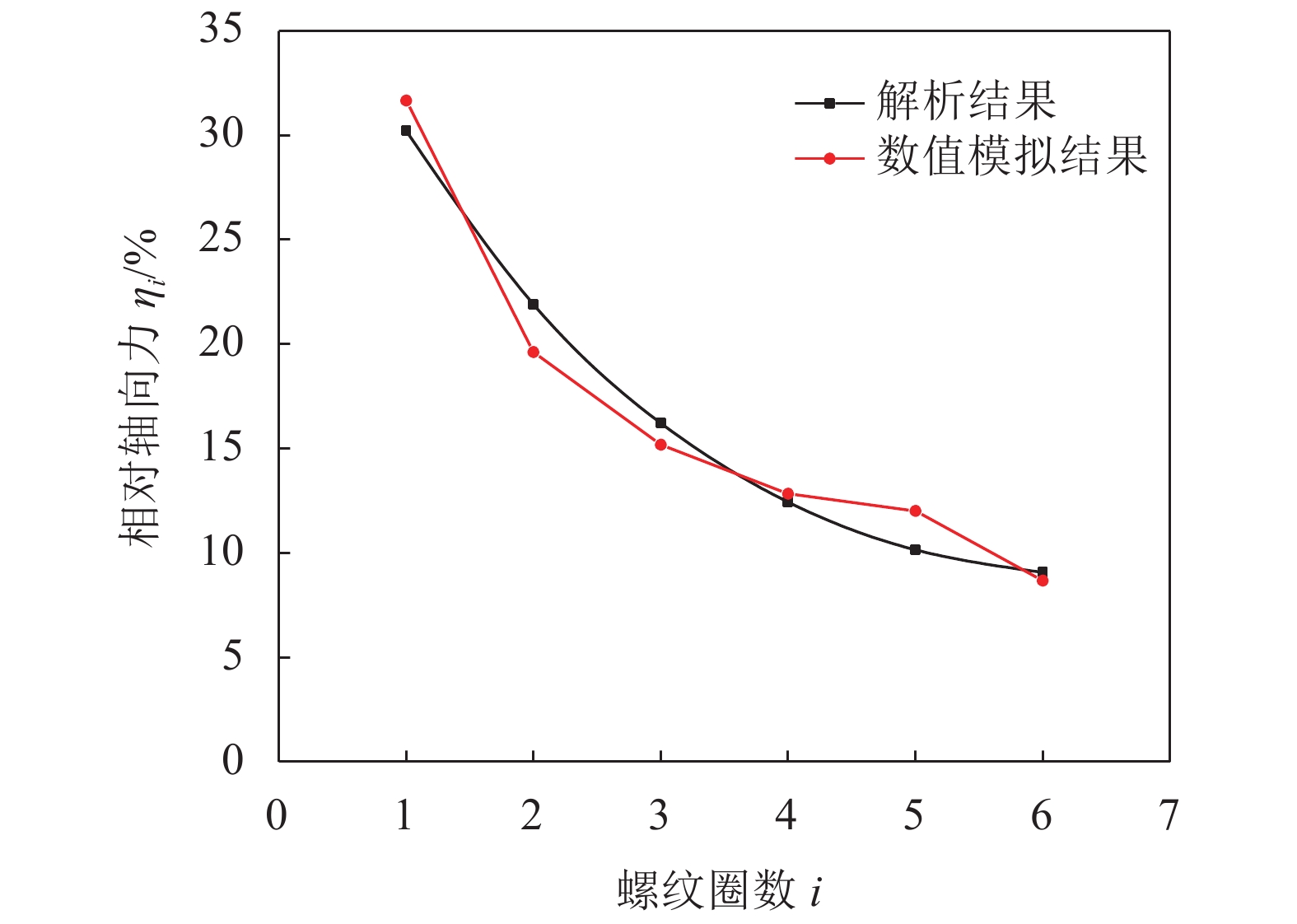 |
| 图14 螺栓螺母各圈螺纹轴向力占比 Fig. 14 Axial force ratio of each cross section of bolts and nuts |
从图14可知:相对轴向力的解析结果和数值模拟结果的最大误差发生在第5圈螺纹处,且误差小于5%;相对轴向力的解析结果和数值结果的平均误差在3%以内;相对轴向力的解析结果和数值结果变化的整体趋势具有一致性。
3.3 螺纹牙底应力集中系数验证现有研究资料[19-20]表明,螺纹连接结构最大应力发生在螺栓螺纹根部,位于一个螺距内的螺母受载表面。使用第1节中获得的带升角的螺纹有限元模型研究螺纹根部周围的应力集中情况。螺纹在受载时,连接件中的载荷分布非常不均匀,有些螺纹可能已经达到塑性阶段,而其他螺纹仅处于弹性状态。螺纹根部存在的严重应力集中往往会导致连接件疲劳失效。应力集中系数
| $ {K_{\rm{t}}} = \frac{{{\sigma _{\max }}}}{{{\sigma _{\rm{n}}}}} $ | (26) |
由于螺纹紧固件的名义应力是螺栓在外力(轴向拉力)作用下缺口处产生的平均应力值,故可将式(26)改写为:
| $ {K_{\rm{t}}} = \frac{{{\sigma _{\max }}}}{{{F_{{\rm{sum}}}}/A}} $ | (27) |
式中,
 |
| 图15 螺栓螺母应力云图 Fig. 15 Stress contour of the bolt and nut |
根据式(26)、(27),计算各螺纹圈上对应的螺纹齿根处应力集中系数
 |
| 图16 各螺纹圈上对应的螺纹齿根处应力集中系数 Fig. 16 Stress concentration factor at the root of each thread ring |
3.4 螺纹表面应力分布
在不改变模型其他设置的情况下,将螺栓/螺母的材料参数加入塑性应变,并重新进行数值计算,得到螺栓上Mises应力分布和最大主塑性应变分布,如图17、18所示。
 |
| 图17 Mises应力云图 Fig. 17 Contour of the equivalent stress |
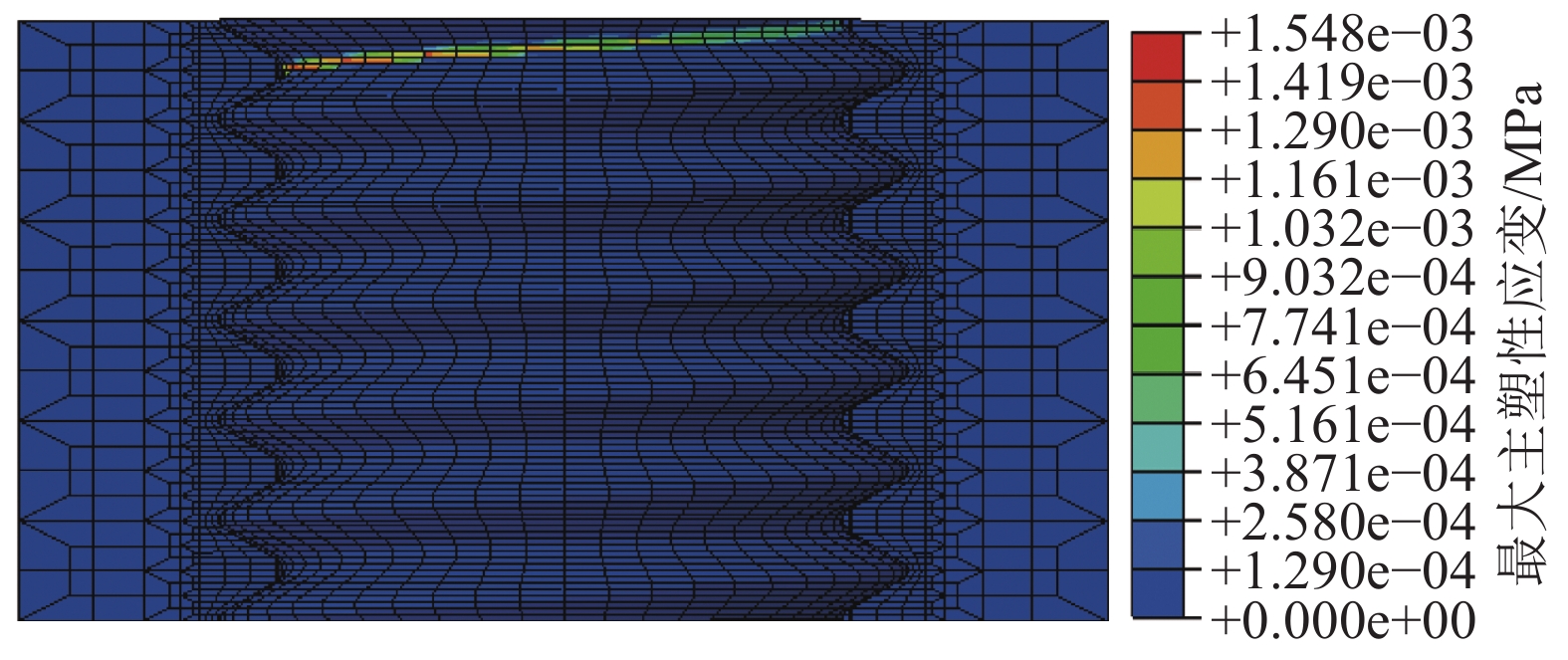 |
| 图18 最大主塑性应变云图 Fig. 18 Contour of the max principal plastic strain |
由图17可知,前3圈螺纹承受载荷最大,且应力的较大值主要集中在螺纹的根部位置,这与第2.2节的理论推导结果及以往的实验结果[24]相符合。由图18可知,塑性形变首先发生在螺栓的第1圈螺纹的根部,而实际工程中螺栓的疲劳断裂也常发生在第1圈螺纹的根部[25-26]。
4 结 论本文基于螺纹紧固件垂直于螺纹轴线的任意横截面形状相同的事实,选用ISO给定的标准螺旋线公式建立了完整的螺纹3维有限元模型。依据该建模方案,在Qt平台上借助OpenGL图形库,开发了一套螺栓螺母有限元参数化建模软件;通过此建模软件对螺纹结构进行参数控制,可以便捷地获取不同型号的螺纹连接件有限元模型。然后,通过数值实验的方法模拟了螺栓的拧紧过程,将数值实验结果与相应理论计算或以往研究进行对比分析,验证了本文建立的模型的有效性和保真性。
| [1] |
Gao Dawei,Gong Jiacheng,Tian Zhongling,et al. Research on bolt pre-tightening and relaxation mechanism under transverse load[J]. Advances in Mechanical Engineering, 2020, 12(12): 1-11. DOI:10.1177/1687814020975919 |
| [2] |
Izumi S,Yokoyama T,Iwasaki A,et al. Three-dimensional finite element analysis of tightening and loosening mechanism of threaded fastener[J]. Engineering Failure Analysis, 2005, 12(4): 604-615. DOI:10.1016/j.engfailanal.2004.09.009 |
| [3] |
Ming Zhang,Jiang Yanyao,Lee C H. Finite element modeling of self-loosening of bolted joints[J]. Journal of Mechanical Design, 2007, 129(2): 218-226. DOI:10.1115/PVP2004-2618 |
| [4] |
Liu Jianhua.Research on the self-loosening mechanism of bolted joints under axial excitation[D].Chengdu:Southwest Jiaotong University,2016. 刘建华.轴向激励下螺栓连接结构的松动机理研究[D].成都:西南交通大学,2016. |
| [5] |
Nassar S A,Yang Xianjie,Gandham S,et al. Nonlinear deformation behavior of clamped bolted joints under a separating service load[J]. Journal of Pressure Vessel Technology, 2011, 133(2): 021001. DOI:10.1115/1.4002674 |
| [6] |
Pai N G,Hess D P. Three-dimensional finite element analysis of threaded fastener loosening due to dynamic shear load[J]. Engineering Failure Analysis, 2002, 9(4): 383-402. DOI:10.1016/S1350-6307(01)00024-3 |
| [7] |
Fukuoka T,Nomura M. Proposition of helical thread modeling with accurate geometry and finite element analysis[J]. Journal of Pressure Vessel Technology, 2008, 130(1): 135-140. DOI:10.1115/PVP2006-ICPVT-11-93165 |
| [8] |
Yokoyama T,Olsson M,Izumi S,et al. Investigation into the self-loosening behavior of bolted joint subjected to rotational loading[J]. Engineering Failure Analysis, 2012, 23: 35-43. DOI:10.1016/j.engfailanal.2012.01.010 |
| [9] |
Verwaerde R,Guidault P A,Boucard P A. A nonlinear finite element connector for the simulation of bolted assemblies[J]. Computational Mechanics, 2020, 65(4): 1531-1548. DOI:10.1007/s00466-020-01833-1 |
| [10] |
Noda N A,Xin C,Sano Y,et al. Effect of pitch difference between the bolt–nut connections upon the anti-loosening performance and fatigue life[J]. Materials and Design, 2016, 96: 476-489. DOI:10.1016/j.matdes.2016.01.128 |
| [11] |
Malla P,Xiong Feng,Cai Gaochuang,et al. Numerical study on the behaviour of vertical bolted joints for precast concrete wall-based low-rise buildings[J]. Journal of Building Engineering, 2020, 33: 101529. DOI:10.1016/j.jobe.2020.101529 |
| [12] |
Shen Xunliang,Lu Liantao,Zeng Dongfang,et al. Improving fatigue resistance of high strength bolt under cyclic transverse loading by fine particle peening[J]. Engineering Structures, 2020, 210: 110359. DOI:10.1016/j.engstruct.2020.110359 |
| [13] |
He Ping,Liu Guangfu,Gu Yeshui,et al. Finite element analysis on bolted joints based on three-dimensional accurate modeling method[J]. China Mechanical Engineering, 2012, 23(16): 1991-1996. [何平,刘光复,谷叶水,等. 基于三维精确建模法的螺栓有限元分析[J]. 中国机械工程, 2012, 23(16): 1991-1996. DOI:10.3969/j.issn.1004-132X.2012.16.022] |
| [14] |
Li Jiuyi,Feng Zhiqiang,Liu Jianhua,et al. A three-dimensional finite element modeling method for spiral thread[J]. Journal of Kunming University of Science and Technology (Natural Science Edition), 2019, 44(5): 132-140. [李九一,冯志强,刘建华,等. 一种螺旋形螺纹三维有限元建模方法[J]. 昆明理工大学学报(自然科学版), 2019, 44(5): 132-140.] |
| [15] |
联邦德国标准化研究所螺纹标准化委员会.国际螺纹手册[M].余志新,徐孝恩,译.北京:中国计量出版社,1988.
|
| [16] |
卜炎.螺纹联接设计与计算[M].北京:高等教育出版社,1995.
|
| [17] |
山本晃.螺纹联接的理论与计算[M].郭可谦,高素娟,王晓凤,等,译.上海:上海科学技术文献出版社,1982.
|
| [18] |
全国紧固件标准化技术委员会.紧固件机械性能螺栓、螺钉和螺柱:GB/T 3098.1—2010[S].北京:中国标准出版社,2011:1
|
| [19] |
Yu Zelin,Sun Pengwen,Wang Dong. Fatigue life prediction for flange connecting bolts of wind turbine tower[J]. Journal of Shanghai Jiaotong University(Science), 2020, 25(4): 526-530. DOI:10.1007/s12204-020-2173-4 |
| [20] |
侯世远,廖日东. 螺纹联接松动过程的研究现状与发展趋势[J]. 强度与环境, 2014, 41(2): 39-52. DOI:10.3969/j.issn.1006-3919.2014.02.007 |
| [21] |
He Xiantong,Lei Honggang,Yan Yajie. Stress concentration analysis of high strength bolts based on different thread forms[J]. Hans Journal of Civil Engineering, 2019, 8(2): 288-294. [贺宪桐,雷宏刚,闫亚杰. 基于不同螺纹形式的高强螺栓应力集中分析[J]. 土木工程, 2019, 8(2): 288-294. DOI:10.12677/HJCE.2019.82035] |
| [22] |
Fukuoka T,Yamasaki N,Kitagawa H,et al. Stresses in bolt and nut:effects of contact conditions at the first ridge[J]. Bulletin of JSME, 1986, 29(256): 3275-3279. DOI:10.1299/jsme1958.29.3275 |
| [23] |
Tafreshi A,Dover W D. Stress analysis of drillstring threaded connections using the finite element method[J]. International Journal of Fatigue, 1993, 15(5): 429-438. DOI:10.1016/0142-1123(93)90490-H |
| [24] |
D’Eramo M,Cappa P. An experimental validation of load distribution in screw threads[J]. Experimental Mechanics, 1991, 31(1): 70-75. DOI:10.1007/BF02325727 |
| [25] |
濮良贵,陈国定,吴立言.机械设计[M].9版.北京:高等教育出版社,2013.
|
| [26] |
Liu Jianhua,Ouyang Huajiang,Ma Lijun,et al. Numerical and theoretical studies of bolted joints under harmonic shear displacement[J]. Latin American Journal of Solids and Structures, 2015, 12(1): 115-132. DOI:10.1590/1679-78251379 |
 2022, Vol. 54
2022, Vol. 54


