2. 四川大学 灾后重建与管理学院,四川 成都 610065;
3. 四川大学 破坏力学与工程防灾减灾四川省重点实验室,四川 成都 610065
2. Inst. for Disaster Management and Reconstruction, Sichuan Univ., Chengdu 610065, China;
3. Failure Mechanics & Eng. Disaster Prevention and Mitigation, Key Lab. of Sichuan Province, Sichuan Univ., Chengdu 610065, China
螺栓连接装配式墙板结构具有施工快捷、绿色环保等优势。近些年,工程应用逐渐广泛,特别是在新农村低多层建筑体系中,显示出强劲的发展前景。目前,通过集中式螺栓节点连接的装配式墙板结构有钢板拼接式螺栓连接和穿缝式螺杆连接等形式,通常在连接上下墙板的水平接缝上安排2~4个连接节点。由于水平缝截面没有均匀的竖向分布钢筋,传力完全依靠螺栓节点,性能不同于现浇墙板结构。现有的试验显示,螺栓连接墙板的初始刚度、破坏模式变形与承载力性能等都与现浇墙有明显的区别。因此,原则上不适合应用“等同现浇”理论设计,必须考虑其受力特点,建立相应的设计方法。
近些年,国内外学者对采用螺栓或螺杆连接的装配式墙板结构进行了深入而广泛的研究。Sun[1]和孙建[2-3]等提出了一种全装配式螺栓连接墙板结构,将预埋有内嵌钢框的预制上下层墙体通过高强螺栓和外部钢框连接起来;试验结果表明,接缝处用钢框架全包边的墙板在抗侧刚度和延性性能方面与装配整体式和现浇墙板相近。赵斌等[4]提出采用螺栓和预埋在墙内的套筒将上下层墙体连接固定到钢框架连接件上,以达到连接上下层墙体的作用;结果表明,装有套筒预制的墙体水平抗剪能力有一定的提高,但对延性和耗能能力的贡献不大。El Semelawy等[5]提出了一种将带肋预制混凝土板拼接成整块墙板的装配式墙板结构体系,在该结构中,螺纹锚杆垂直于水平或竖向接缝穿过相邻混凝土板上预留的孔洞,将各预制构件连接成整体墙板;试验结果表明,由于锚杆和混凝土之间没有黏结,地震引起的结构损伤和破坏主要集中在锚杆上。薛伟辰[6-7]等提出一种竖向采用螺栓钢筋连接,楼板采用装配整体式的混凝土墙板体系。类似地,李思婷[8]和王小平[9]等利用竖向螺栓穿过预制混凝土夹芯墙板上的预留孔洞,实现相邻构件的全装配式连接。Psychairs等[10]提出了两种连接方式:一是,利用锚固在梁内的竖向螺栓穿过预埋在上层墙体的“墙靴”进行连接;二是,在预制构件中预埋连接件,通过连接钢板和螺栓将相邻构件连接起来。黄少腾等[11]针对含有水平缝的墙板,采用外侧双钢板–内部混凝土墙板的组合,通过螺栓将上下层墙体和整块盖板连接起来。Vaghei等[12]研究了由螺纹接头和螺母组成的组合接头水平连接预制墙板的抗震性能。Chen等[13]研究了带有普通强度钢板螺栓连接的两层预制混凝土墙板的力学性能。Guo等[14]提出了一种由锚定钢板和高强度螺栓组成的螺栓连接,用于墙板或基础之间的连接,锚固钢板与钢筋之间的连接需要焊接。Sun等[15]利用“H”型钢连接器连接上下相邻的墙板,通过连接器和面板上的预设孔,用高强度螺栓固定面板。徐咏[16]和王威[17]等提出了一种装配式墙板螺栓连接方案,通过在预制墙板中预留螺栓孔,采用前后两块钢板作为连接件,将上下墙板用螺栓拼接在一起,用于低多层装配式墙板住宅。Chen[13]和陈文[18]等通过墙板构件与整体缩尺结构的拟静力加载,进行了抗震性能试验研究,并提出了相应的承载力设计公式。上述研究主要集中在螺栓连接的形式和构造,以及相关结构的抗震性能方面,大都根据试验研究的结果,汇总分析各参数对承载能力、变形能力等方面的影响,而对螺栓连接墙板结构的抗侧刚度和变形计算缺乏深入研究,导致螺栓连接装配式墙板体系设计理论还不完善。
墙板结构的抗侧刚度是基本周期计算和水平地震力分配等结构设计的重要参数。同时,由于预制构件之间存在接缝,接缝处的连接节点更易于在外力作用下产生变形,使得预制结构的抗侧刚度不同于整体现浇结构[19]。因此,本文通过螺栓连接墙板结构拟静力试验、侧向变形理论分析及数值模拟,研究螺栓连接墙板体系的变形特征,提出抗侧刚度的计算方法,为建立低多层螺栓连接装配式墙板结构体系的设计理论提供参考。
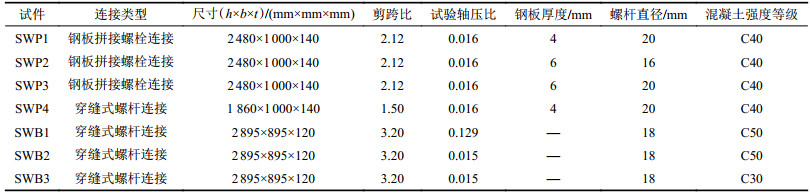
1 试验概况图1为干式螺栓连接预制墙板结构。对图1(a)和(b)两种螺栓连接形式,进行7个试件的拟静力试验,研究不同轴压比或剪跨比下,干式连接预制墙板的力学性能。其中,轴压比为0.016和0.129,分别对应低层建筑和多层建筑的应用场景,试件的基本参数见表1。
 |
| 图1 干式螺栓连接预制墙板结构 Fig. 1 Dry-type bolted prefabricated concrete wall |
| 表1 干式螺栓连接预制墙板试件基本参数 Tab. 1 Specimen parameters of dry-type bolted prefabricated concrete wall |
 |
两种螺栓连接预制墙板的构造和节点如图2所示。典型的骨架曲线和试件破坏形态见图3和4。从图3可知:螺栓连接装配式墙板有较好的整体性能,能有效地抵抗水平荷载,其破坏过程受剪压比、轴压比等参数的影响,不同轴压比下墙板的力学性能差异明显。较高轴压比可显著提高试件在反复荷载下的承载能力和初始刚度,但同时也会降低试件的极限变形能力;较高轴压比试件SWB1在破坏时将呈现出脆性破坏的特征。归纳起来,试件墙的受力特点如下:
 |
| 图2 螺栓连接预制墙板构造及节点 Fig. 2 Detail of bolted precast wall construction and joints |
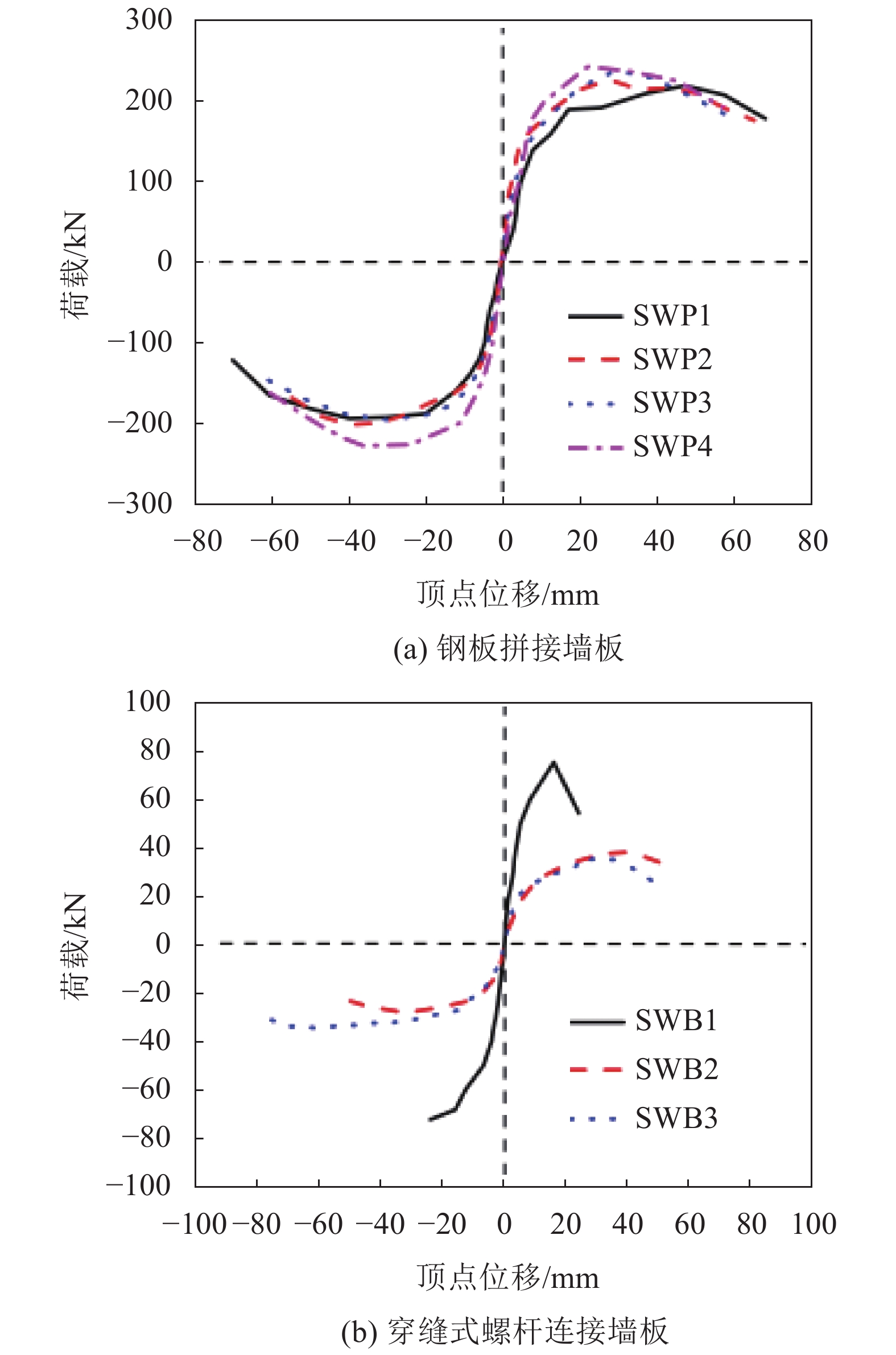 |
| 图3 骨架曲线 Fig. 3 Skeleton curves |
1)弹性阶段。当荷载较小时,墙体处于弹性阶段,骨架曲线表现为直线,初始抗侧刚度小于相应的现浇墙体。如果轴压比较小,试件在加载初期会沿水平缝开裂,形成明显的座浆层裂缝。
2)裂缝阶段。试件裂缝一般首先出现在受拉节点一侧,从螺栓位置沿斜向延伸,逐渐形成“八”字形冲切裂缝;同时,在受压节点处形成竖向劈裂型裂缝(图4)。
 |
| 图4 螺栓连接预制墙板的破坏形态 Fig. 4 Failure mode of bolted prefabricated concrete wall |
3)屈服阶段。当荷载加到屈服后,冲切裂缝与劈裂裂缝逐渐加宽;同时,墙体中下部出现水平裂缝,受压区混凝土出现轻微损伤。
4)破坏阶段:随着荷载进一步增加,钢板或螺栓均有滑移现象,整体结构发生了明显的倾斜位移。受压区混凝土不断剥落,钢筋裸露,承载力下降至峰值荷载的85%,表明结构破坏。
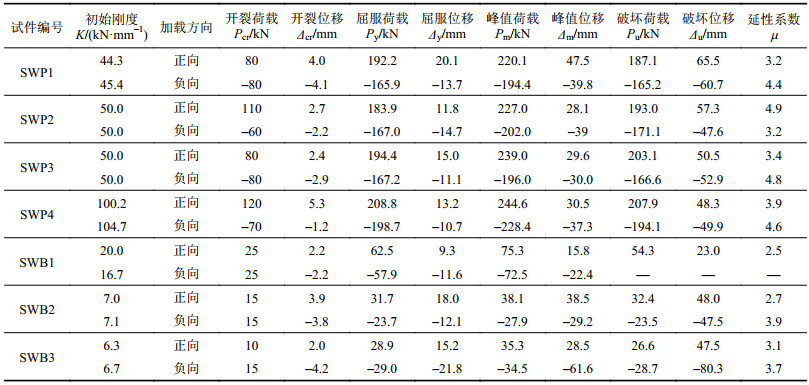
从图3和4还可以看出:与现浇墙板相比,螺栓连接墙板首先会在水平缝处张开,使墙体发生刚性转动,而由弯矩产生的墙体本身的水平裂缝较少;随着荷载的增加,钢板和螺栓等金属件使混凝土局部应力增大,造成节点附近混凝土开裂,形成“八”字形冲切裂缝与受压劈裂裂缝,而由于螺栓节点区域混凝土局部加强,冲切与劈裂裂缝并没有成为破坏控制因素;最后的破坏模式仍然是墙趾部位受压区混凝土的压溃,而非螺栓节点局部的冲切破坏,说明墙体混凝土材料得到充分发挥,结构具有较好的承载力。同时,墙体表现出较好的变形性能,骨架曲线平滑,没有出现螺栓滑移导致的变形突变,延性系数一般大于3。表2为各试件的承载力和变形特征值。其中,屈服位移通过能量等效原则进行计算,具体计算方法参考文献[20]。
| 表2 各试件的承载力和变形特征值 Tab. 2 Characteristic load capacity and deformation capacity of specimens |
 |
2 螺栓连接墙板弹性受力分析 2.1 弹性理论分析
受力初期,螺栓连接墙板由于水平缝张开,水平缝截面中和轴会发生偏移,同时受压区面积减小,如图5所示。截面拉力由螺栓节点传递,压力主要由受压区混凝土接触传递。水平缝的张开使得墙体发生刚体旋转,导致顶部水平变形增大(图5(b))。同时,由于剪力作用,当水平缝处克服了受压区的摩擦力后,上部墙体将沿水平缝产生滑移,也将增大墙体的水平位移。因此,相比现浇墙板,螺栓连接墙板的刚度将明显下降。
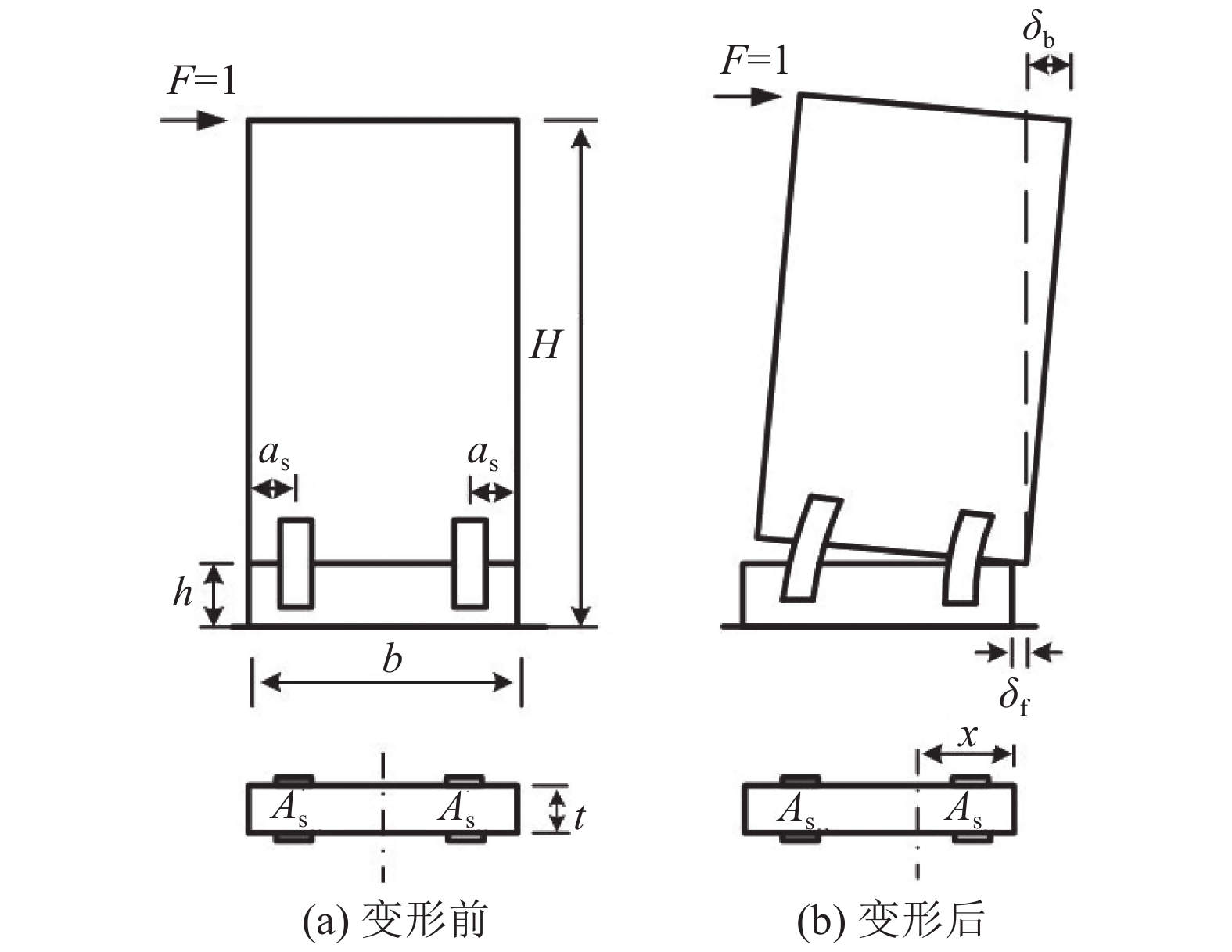 |
| 图5 螺栓连接墙板的水平变形形态 Fig. 5 Horizontal deformation feature of bolted prefabricated wall |
为分析螺栓连接墙板的初始刚度,假设墙体尺寸如图5(a)所示。图5中:墙高为H,宽度为b,厚度为t,连接节点中心距边缘距离为as,节点的钢材截面面积为As(对于钢板拼接式连接为连接钢板的截面面积,对于穿缝式螺杆连接为螺杆截面面积)。悬臂墙板受单位水平力作用,顶部的水平总位移为δ,则初始抗侧刚度
由于水平缝的存在,受拉区混凝土不传递拉力,仅靠螺栓节点承受拉力,但受压区混凝土传递压力,因此,中和轴不再保持在中心,受压区宽度x取决于水平缝截面的受力平衡(图5(b))。根据力矩平衡和平截面假定,可确定受压区的宽度x与混凝土截面的惯性矩If。其中,x为:
| $ xt\times {E}_{{\rm{c}}}{\varepsilon }_{{\rm{c}}}\times \frac{2}{3}x+{A}_{{\rm{s}}}\times {E}_{{\rm{s}}}{\varepsilon }'_{{\rm{s}}}{{}}\times \left(x-{a}_{{\rm{s}}}\right) ={A}_{{\rm{s}}}\times {E}_{{\rm{s}}}{\varepsilon }_{{\rm{s}}}\times \left(b-x-{a}_{{\rm{s}}}\right) $ | (1) |
式中:Es与Ec分别为钢材与混凝土的弹性模量;εc为受压区混凝土应变;εs为受拉钢板或螺杆应变,
惯性矩If为:
| $ {I}_{{\rm{f}}}=\frac{t{b}^{3}}{\text{12}}-\frac{bt{\left(b{-2}x\right)}^{2}}{4} $ | (2) |
在水平荷载作用下,螺栓连接预制墙板顶部位移为:
| $ {\;\;\;\;\;\;\;\;\; \delta ={\delta }_{{\rm{w}}}+{\delta }_{{\rm{b}}}+{\delta }_{{\rm{f}}}={\delta }_{\text{wM}}+{\delta }_{\text{wV}}+{\delta }_{{\rm{b}}}+{\delta }_{{\rm{f}}} }$ | (3) |
式中,
根据弹性理论,对于悬臂墙有:
| $ {\delta }_{\text{wM}}=\frac{{H}^{3}}{3E{I}_{{\rm{w}}}} $ | (4) |
| $ {\delta }_{\text{wV}}=\frac{H}{\xi G{A}_{{\rm{w}}}} $ | (5) |
式(4)和(5)中:EIw和GAw为墙截面的抗弯与抗剪刚度,根据《混凝土结构设计规范》(GB 50010—2010)[21],混凝土的剪切变形模量可按相应弹性模量值的40%采用,即G=0.4E;
为确定
| $ \varphi =\frac{M}{{E}_{{\rm{c}}}{I}_{{\rm{f}}}}=\frac{H-h}{{E}_{{\rm{c}}}{I}_{{\rm{f}}}} $ | (6) |
因此,螺栓节点的轴向应变为:
| $ {\varepsilon }_{{\rm{b}}}=\varphi \left(b-{a}_{{\rm{s}}}-x\right) $ | (7) |
假设节点中连接钢板或穿缝螺杆的长度为lb,可得节点的受拉位移
| $ \theta =\frac{{{\mathit{\Delta}} }_{{\rm{b}}}}{b-{a}_{{\rm{s}}}-x}=\varphi {l}_{{\rm{b}}}=\frac{H-h}{{E}_{{\rm{c}}}{I}_{{\rm{f}}}}{l}_{{\rm{b}}} $ | (8) |
由此产生的墙体顶部水平位移为:
| $ {\delta }_{{\rm{b}}}=\theta \left(H-h\right)=\frac{{\left(H-h\right)}^{2}}{{E}_{{\rm{c}}}{I}_{{\rm{f}}}}{l}_{{\rm{b}}} $ | (9) |
当水平缝剪切滑动时,连接钢板或者螺杆将随之发生变形,如图6所示。
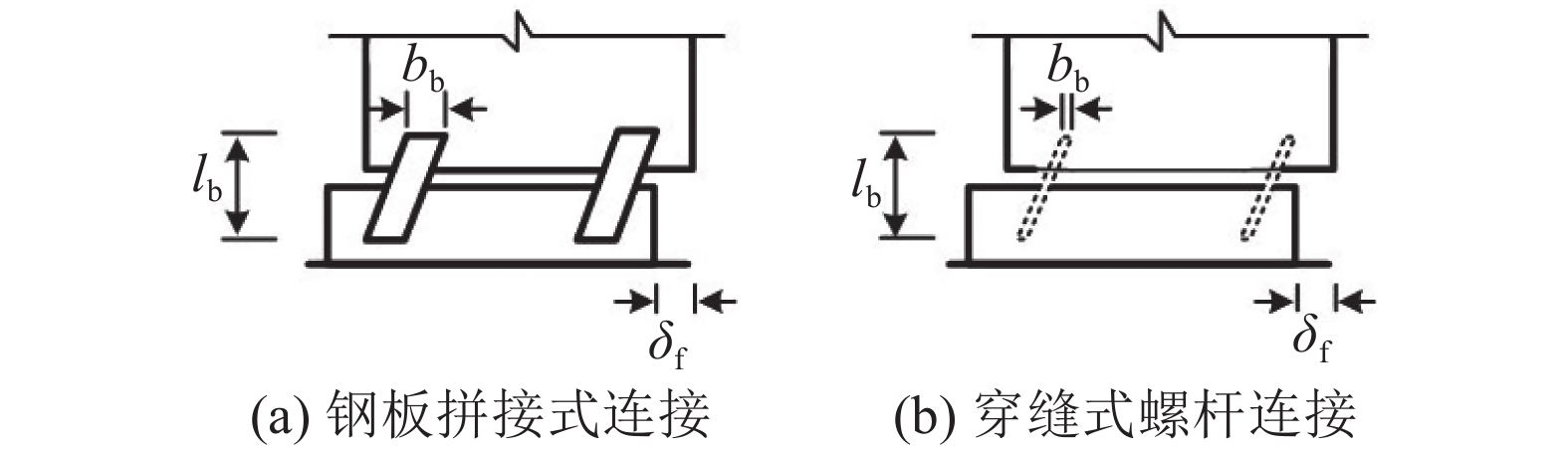 |
| 图6 水平缝剪切滑动位移 Fig. 6 Shear displacement of horizontal connection |
由图6(a)可见,连接钢板将发生弯曲与剪切变形,可将其视为下端固定、上端滑动的梁单元,因此水平缝位移为:
| $ {\delta }_{{\rm{f}}}=\frac{{l}_{{\rm{b}}}}{n\xi {G}_{{\rm{s}}}{A}_{{\rm{s}}}}+\frac{{l}_{{\rm{b}}}^{3}}{\text{12}n{E}_{{\rm{s}}}{I}_{{\rm{s}}}} $ | (10) |
式中:n为连接钢板的个数,本文n=2;
由图6(b)可知,由于螺栓孔最后要填埋砂浆,因此,在水平缝滑动时,螺栓仅产生剪切变形,水平缝位移为:
| $ {\delta }_{{\rm{f}}}=\frac{{l}_{{\rm{b}}}}{n\xi {G}_{{\rm{s}}}{A}_{{\rm{s}}}} $ | (11) |
由式(12):
| $ K=\frac{1}{\delta }=\frac{1}{{\delta }_{\text{wM}}+{\delta }_{\text{wV}}+{\delta }_{{\rm{b}}}+{\delta }_{{\rm{f}}}} $ | (12) |
叠加式(4)~(11),可求得螺栓连接墙板的初始刚度。
2.2 有限元分析为进一步分析螺栓连接预制墙板的受力性能,采用有限元分析软件ABAQUS,对螺栓连接墙板试件及相应的现浇墙板进行弹性有限元分析。
2.2.1 材料本构关系预制装配式墙板中的钢筋、钢板及高强度螺栓的材料均为钢材。由于本文仅涉及弹性分析,因此,钢材采用理想弹塑性模型。钢板为Q235钢材,纵横向钢筋为HRB400,螺栓采用8.8级高强螺栓。根据《钢结构设计标准》(GB50017—2017)[22]对给定的材料强度设计值进行取值。混凝土轴向受拉时,由于抗拉强度比较低,而比例极限又比较高,因此假定混凝土的应力–应变关系为直线,受拉时的弹性模量等于受压时的初始弹性模量。
2.2.2 单元类型、网格划分和接触条件模型中,混凝土和钢结构部分采用八节点线性实体缩减积分单元C3D8R进行模拟。钢板网格尺寸为5 mm;螺栓网格尺寸为2 mm;钢筋采用两节点3维桁架单元T3D2模拟,网格尺寸为10 mm。装配式墙板与现浇墙板基础设为固结,钢筋单元与混凝土单元之间的接触设置为Embedded。法向界面接触采用软件默认的“硬”接触,切向界面接触采用罚函数接触;水平缝混凝土间的摩擦系数设为0.35,钢板与混凝土间的摩擦系数设为0.20。通过试算可知,选用的网格尺寸能够保证计算精度和结果收敛。
2.2.3 结果分析为分析螺栓连接墙板变形特征,以SWP墙板试件为例,提取结构的竖向应变与竖向位移云图,如图7所示。由图7(b)和(d)可以看出,现浇墙板竖向应变与竖向位移均对称,表明截面中和轴在中间,符合悬臂梁的变形特征。由图7(a)和(c)可知:螺栓连接预制墙板截面受压区明显减少,应变分布不对称,受拉钢板应变水平远高于受压钢板;从竖向变形来看,也呈不对称的状态,每个截面左边受拉竖向位移大于右边受压位移,且相差一个定值(1.3×10–5 mm),这个差值可以看作为受拉钢板的变形Δs。由于存在竖向变形差,导致墙体产生刚体转动,引起墙体顶点水平位移的增加,验证了理论分析的结果。
 |
| 图7 竖向应变与竖向位移 Fig. 7 Vertical strain and displacement |
图8为现浇墙板和螺栓连接预制墙板沿高度方向的水平位移分布情况。由图8可见,螺栓连接预制墙板的水平位移始终大于现浇墙板的位移,且差异随高度增加而增大。这一现象表明螺栓连接预制墙板的整体抗侧刚度较现浇墙板低。同时,现浇墙板变形呈明显的弯曲特征,下部变形小,上部变形大;而螺栓连接预制墙板的位移则接近直线,具有刚体位移的特征。
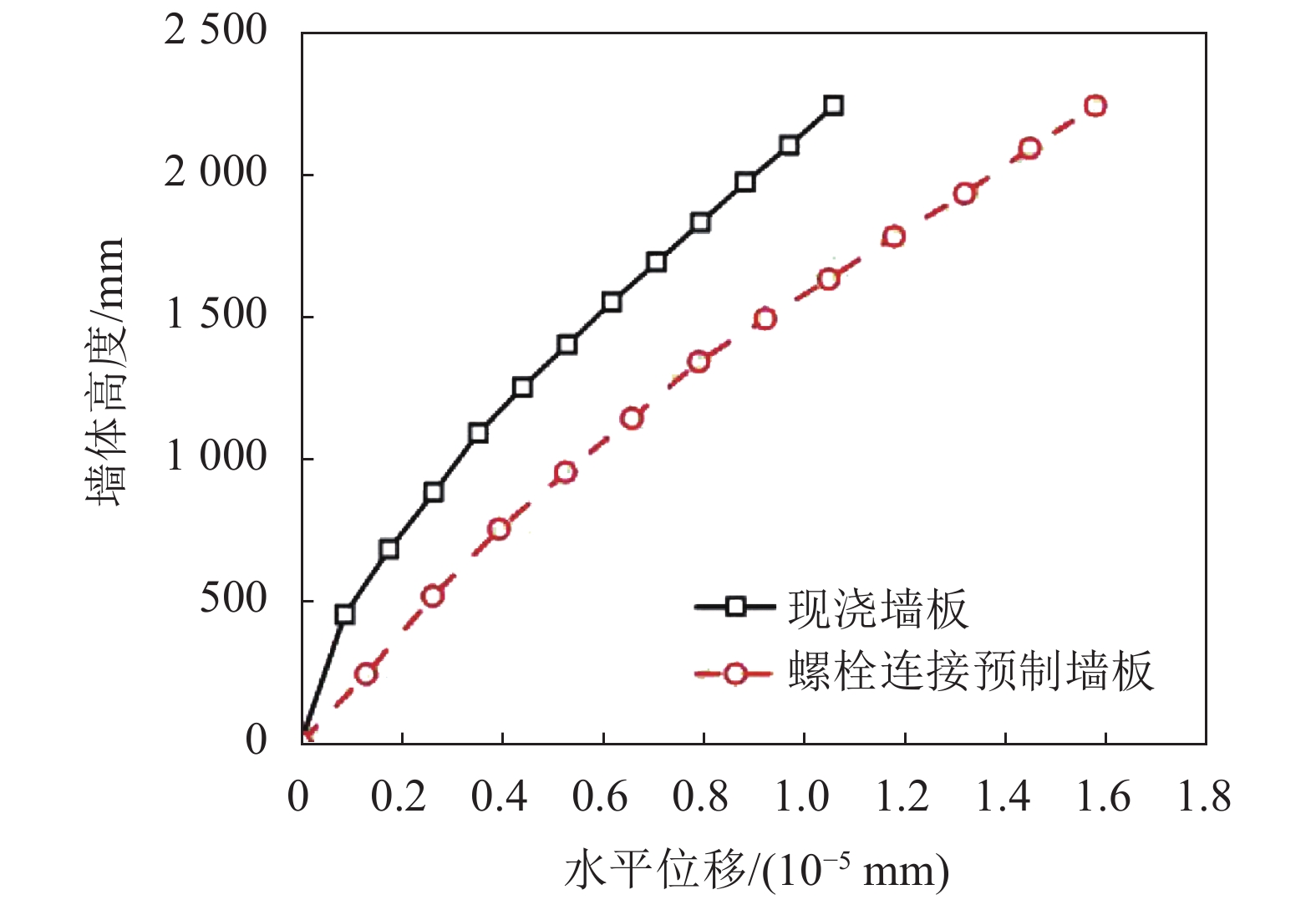 |
| 图8 墙体高度和水平位移的关系 Fig. 8 Relationship between the height of the wall and horizontal displacement |
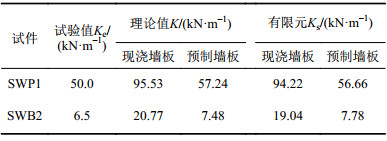
表3为螺栓连接预制墙板和现浇墙板的初始刚度对比结果。其中,理论计算依据公式(12)进行。由表3可以看出:1)有限元模拟结果与理论计算结果吻合良好,误差不超过5%,说明理论公式是可靠的。2)螺栓连接预制墙板的刚度试值低于现浇墙板的刚度,SWP1墙板刚度约为现浇墙板的52%,SWB2墙板约为现浇墙板的31%;通过第3节影响因素分析可知,控制螺栓节点配钢率可使螺栓连接预制墙板刚度显著提高,甚至等同于现浇墙板。3) 理论计算的初始刚度略高于试验测得的初始刚度,SWP1和SWB2墙板相对误差分别为14.48%和15.07%。造成误差的原因是螺栓连接预制墙板与加载梁采用螺杆连接,存在安装缝隙,当结构加载时,会出现初始的微小滑移,导致刚度试验值较理论值略低[3]。
| 表3 螺栓连接预制墙板和现浇墙板的初始刚度对比 Tab. 3 Comparison of initial stiffness between bolted prefabricated wall and cast-in-place concrete wall |
 |
3 抗侧刚度影响因素分析
螺栓连接装配式墙板的初始刚度主要取决于4个因素:墙体的高宽比(H/b)、连接节点的抗拉刚度(EsAs)、节点的相对位置(as/b)中及轴压比。从表1可以看出,试件SWB1和SWB2的轴压比分别为0.129和0.015,其平均初始刚度分别为18.35 和6.55 kN/mm ,表示SWB1比SWB2的初始刚度高2.8倍。在竖向压力作用下,悬臂墙水平缝的张开将受到限制,随着轴压比的增大,带水平缝的螺栓连接预制墙板的初始刚度将逐渐接近现浇墙板。
为了分析螺栓连接墙板的初始刚度相对现浇墙的变化,定义刚度降低系数如下:
| $ \gamma=\frac{K}{K_{0}} $ | (13) |
式中:K为螺栓连接墙板的初始刚度;K0为相同尺寸的现浇墙板的抗侧刚度,K0的计算公式为:
| $ {K}_{0}=\frac{1}{{\delta }_{\text{wM}}+{\delta }_{\text{wV}}} $ | (14) |
定义参数:墙体的高宽比
为研究影响螺栓连接预制墙板初始刚度的影响因素,使用有限元法模拟进行参数分析,以SWP1试件为例,改变参数β、μ、
 |
| 图9 刚度降低系数与各参数的关系 Fig. 9 Relationship between stiffness reduction coefficient and several factors |
1)螺栓节点配钢率
由图9(a)墙体刚度降低系数与螺栓节点配钢率之间的关系可以看出,在β=2.24、α=0和
2)墙体的高宽比
由图9(b)墙体刚度降低系数与墙体高宽比之间的关系可以看出,在μ=1.29%、α=0和
3)节点的相对位置
由图9(c)墙体刚度降低系数与节点相对位置之间的关系可以看出,在µ =1.29%、β=2.24和α=0时,随着节点的相对位置增大(即节点和墙体边缘的距离增大),刚度降低系数基本呈线性下降。原因是节点越靠近墙体边缘,对水平缝的约束作用越强,抗侧刚度则越大。
4)轴压比
图9(d)为考虑了不同高宽比和不同配钢率,节点的相对位置取0.2时,轴压比对墙体刚度降低系数的影响。由图9(d)可以看出:轴压比的影响存在门槛值,只有当轴压比较小(< 0.2)时,带水平缝装配式墙体的刚度才会下降;当轴压比>0.2时,刚度降低系数则为1,即螺栓连接墙与现浇墙刚度相同。原因在于当轴压比较大时,对水平缝张开有较强的抑制作用,使得装配式墙不产生刚性转动,因此刚度不会下降。当螺栓连接装配式墙板应用于低多层建筑时,通常轴压比较小,因此需要考虑初始刚度的下降;用于高层建筑时,轴压比通常大于0.2,可以不考虑螺栓连接墙板初始刚度的下降。此外,对比图8中的3条曲线可以得出:①对于不同的节点配钢率,轴压比对墙体刚度降低系数的影响规律基本不变。②对于不同的高宽比,影响墙体刚度降低系数的轴压比临界值发生改变,高宽比为2.24时,轴压比临界值约为0.2;当高宽比为3.24时,该门槛值在0.1附近。
4 初始刚度降低系数简化计算公式采用式(1)~(14)可以计算出螺栓连接装配式墙板的初始刚度降低系数,但上述公式存在以下几点不足:
1)未考虑轴压比的影响,即只适合于α=0的情况。从有限元模拟的结果可以看出,当轴压比低于门槛值时,随着轴压比的降低,刚度降低系数下降较快。
2)计算过程较为繁琐,涉及的参数较多,不便于工程设计人员使用。
当设计螺栓连接装配式墙板结构体系时,如能首先确定墙体的初始刚度下降系数,便可以利用现行的结构设计方法,按照现浇体系进行计算,进而确定体系的位移和各墙体的截面内力。因此建立初始刚度降低系数的简化公式非常必要。
4.1 形式假定从图9(a)和(b)可以看出,节点配钢率和墙体高宽比对刚度降低系数的影响符合对数分布,公式形式假定为:
| $ y=a \times \ln\; x+b $ | (15) |
节点相对位置对刚度降低系数的影响基本呈线性(图9(c)),公式形式假定为:
| $ y=a x+b $ | (16) |
从图9(d)可以看出:当轴压比趋近于0.2时,刚度降低系数为1;当轴压比趋近于0时,刚度降低系数与另外3个参数相关。因此,假定轴压比的影响遵循下列关系式:
| $ y=\left\{\begin{array}{c}a{x}^{b}+c,x=0,y=c;\\ a{x}^{b}+1,x=1,y=1\end{array}\right. $ | (17) |
综上,初步将刚度降低系数的计算公式假定为:
| $ \gamma =a\text{ln}\;\mu+b\text{ln}\;\beta +\frac{c{\alpha }^{d}+e}{c{\alpha }^{d}+1}+f{\xi }_{{\rm{a}}} $ | (18) |
式中,a、b、c、d、e和f为回归系数。
4.2 回归公式通过改变节点配钢率、墙体高宽比、轴压比和节点相对位置参数,采用数值模型进行参数分析,得到不同参数组合下的刚度降低系数。在进行了202组数值模拟后,采用式(18)进行回归分析。回归系数取值为:a=0.05、b=0.29、c=104、d=3、e=0.71和f=–0.37,回归公式如式(19)所示:
| $ \begin{aligned}[b]& \gamma=0.05 \ln \;\mu+0.29 \beta+\dfrac{10^{4} \alpha^{3}+0.71}{10^{4} \alpha^{3}+1}-0.37 \xi_{{\rm{a}}}, \\& \qquad \qquad \qquad\qquad\quad\gamma \le 1.0 \end{aligned} $ | (19) |
有限元模拟结果与回归公式计算结果的对比如图10所示。由图10可以看出:数据虽具有一定的离散性,但大多数数据点都较为靠近直线Y=X,即回归公式的计算结果接近数值模拟结果;除图10中圈出的数据点外,约93%数据点在±20%的误差区间内,平均误差为–1.4%,标准差为0.08,数据误差较大(>20%)的点有13个,汇总至表4中。
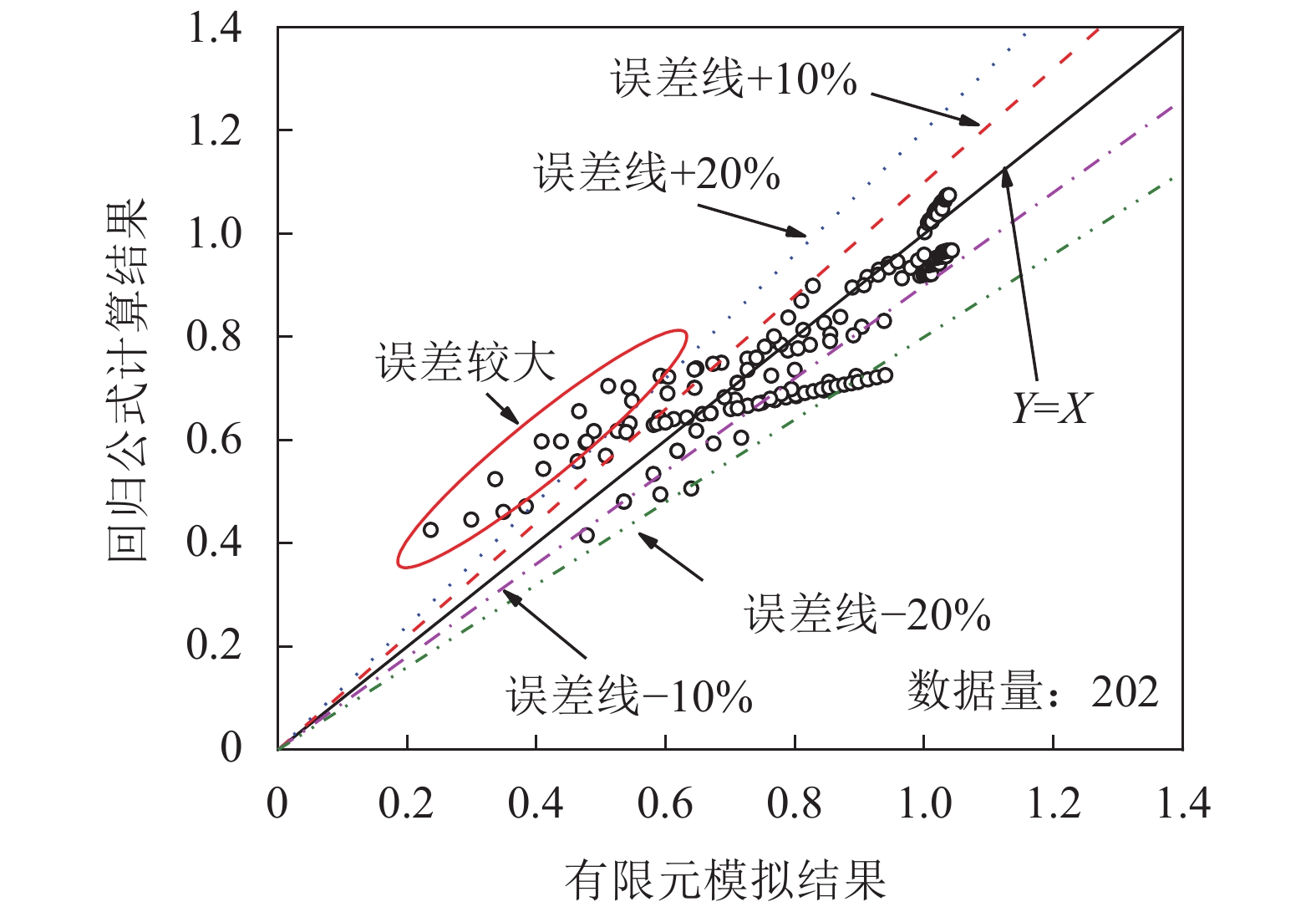 |
| 图10 回归公式计算结果与有限元模拟结果的对比 Fig. 10 Comparison between the calculation results of regression formula and simulation results |
| 表4 图10中相对误差较大(>20%)的数据点汇总 Tab. 4 Summary of data in Fig.10 with relative error over 20% |
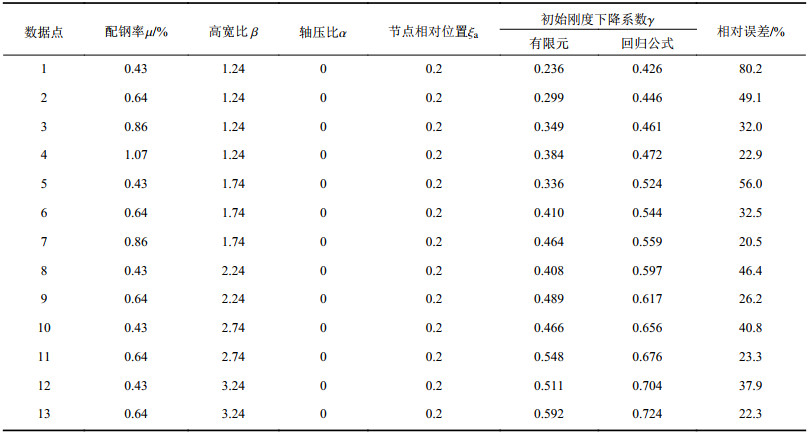 |
图11汇总了202个数据点的相对误差值与各参数的关系。通过对比表4和图11可以看出,误差较大的数据点通常具有较低的配钢率(<1%),实际上以本文研究的SWP试件为例,厚度为4和6 mm钢板的配钢率分别为1.7%和2.5%,一般情况下不会采用更薄或者更窄的钢板。因此,整体上说,本文提出的回归公式能较好地表达参数对刚度降低系数的影响。综上,回归公式(19)作为求解干式螺栓连接预制墙板初始刚度降低系数的简化公式可以较为准确地给出预测结果,公式简单,便于设计人员使用。
 |
| 图11 有限元和回归公式求得的刚度降低系数的相对误差与各参数的关系 Fig. 11 Relationship between the relative error of stiffness reduction coefficient from FEM and regression formula and several factors |
5 结 论
1)螺栓连接装配式墙板拟静力试验结果显示:墙体受力后由于水平缝处张开,墙体发生刚性转动,导致抗侧刚度低于现浇墙板;最终破坏形态是墙趾部位受压区混凝土的压溃,而非螺栓节点局部的冲切破坏,说明结构墙具有较好的承载力。同时,螺栓连接装配式墙板骨架曲线平滑,说明墙体变形性能良好。
2)通过螺栓连接装配式墙板的弹性理论受力分析,揭示了水平缝张开导致的墙体转动位移和水平缝剪切滑动位移是墙体初始刚度下降的主要因素。在此基础上,提出了螺栓连接装配式墙板的初始刚度计算公式,并通过有限元分析,验证了所提公式的可靠性。
3)螺栓连接装配式墙板有限元参数分析的结果表明:螺栓节点配钢率越高,墙体的高宽比越大,抗侧刚度降低系数越大;随着螺栓节点至墙体边缘的距离增大,刚度降低系数呈线性下降;在低轴压比情况下,墙体轴压比越高,刚度降低系数越高,但当轴压比达到一定值(如0.2)后,刚度降低系数趋向于1。
4)基于参数分析的研究结果,回归了考虑螺栓节点配钢率、墙体的高宽比、轴压比和节点相对位置4个参数在内的干式螺栓连接装配式墙板抗侧刚度降低系数的简化计算公式。通过对比该简化公式的计算结果与数值模拟的结果,得出大多数(约93%)数据点的误差在±20%之内,表明预测结果较为准确。
| [1] |
Sun Jian,Qiu Hongxing,Lu Yong. Experimental study and associated numerical simulation of horizontally connected precast shear wall assembly[J]. The Structural Design of Tall and Special Buildings, 2016, 25(13): 659-678. DOI:10.1002/tal.1277 |
| [2] |
Sun Jian,Qiu Hongxing,Tan Zhicheng,et al. Experimental study on mechanical behavior of rectangular precast reinforced concrete shear wall utilizing bolted connections[J]. Journal of Building Structures, 2016, 37(3): 67-75. [孙建,邱洪兴,谭志成,等. 螺栓连接全装配式一字形RC剪力墙受力性能试验研究[J]. 建筑结构学报, 2016, 37(3): 67-75. DOI:10.14006/j.jzjgxb.2016.03.009] |
| [3] |
Sun Jian.Study on the seismic behavior of an innovative totally precast shear wall structure[D].Nanjing:Southeast University,2016. 孙建.新型全预制装配式剪力墙结构抗震性能研究[D].南京:东南大学,2016. |
| [4] |
Zhao Bin,Wang Qingyang,Lyu Xilin. Research on seismic behavior of precast concrete walls with fully assembled horizontal joints[J]. Journal of Building Structures, 2018, 39(12): 48-55. [赵斌,王庆杨,吕西林. 采用全装配水平接缝的预制混凝土剪力墙抗震性能研究[J]. 建筑结构学报, 2018, 39(12): 48-55. DOI:10.14006/j.jzjgxb.2018.12.006] |
| [5] |
El Semelawy M,El Damatty A,Soliman A M. Novel anchor-jointed precast shear wall:Testing and validation[J]. Proceedings of the Institution of Civil Engineers–Structures and Buildings, 2015, 168(4): 263-274. DOI:10.1680/stbu.14.00011[LinkOut |
| [6] |
Xue Weichen,Gu Xuli,Hu Xiang,et al. Experimental study of assembled monolithic concrete shear wall with bolted connection under low reversed cyclic loading[J]. China Civil Engineering Journal, 2014, 47(Supp2): 221-226. [薛伟辰,古徐莉,胡翔,等. 螺栓连接装配整体式混凝土剪力墙低周反复试验研究[J]. 土木工程学报, 2014, 47(增刊2): 221-226. DOI:10.15951/j.tmgcxb.2014.s2.036] |
| [7] |
Xue Weichen,Chu Mingxiao,Liu Yanan,et al. Seismic performance of new precast concrete shear wall under high axial compression ratio[J]. Journal of Harbin Engineering University, 2018, 39(3): 452-460. [薛伟辰,褚明晓,刘亚男,等. 高轴压比下新型预制混凝土剪力墙抗震性能[J]. 哈尔滨工程大学学报, 2018, 39(3): 452-460. DOI:10.11990/jheu.201710033] |
| [8] |
Li Siting.Experimental research and finite element analysis on vertical bearing capacity of precast concrete wall panel[D].Wuhan:Wuhan University of Technology,2016. 李思婷.装配式预制混凝土墙板竖向承载力试验研究与分析[D].武汉:武汉理工大学,2016. |
| [9] |
Wang Xiaoping,Huang Pengfei,Li Siting. Experimental research and analysis on vertical bearing capacity of precast concrete wall[J]. Concrete, 2019(3): 134-139. [王小平,黄鹏飞,李思婷. 装配式预制混凝土墙板竖向承载力试验研究与分析[J]. 混凝土, 2019(3): 134-139. DOI:10.3969/j.issn.1002-3550.2019.03.032] |
| [10] |
Psycharis I N,Kalyviotis I M,Mouzakis H P. Experimental investigation of the response of precast concrete cladding panels with integrated connections under monotonic and cyclic loading[J]. Engineering Structures, 2018, 159: 75-88. DOI:10.1016/j.engstruct.2017.12.036[LinkOut |
| [11] |
Huang Shaoteng,Huang Yansheng,Cai Jian,et al. Seismic behavior test of steel-concrete-steel composite shear wall with vertical seams and horizontal bolt connections[J]. Journal of Building Structures, 2021, 42(7): 164-172. [黄少腾,黄炎生,蔡健,等. 设置竖向通缝的螺栓连接双层钢板-混凝土组合剪力墙抗震性能试验[J]. 建筑结构学报, 2021, 42(7): 164-172. DOI:10.1016/j.engstruct.2017.12.036] |
| [12] |
Vaghei R,Hejazi F,Firoozi A A,et al. Performance of loop connection in precast concrete walls subjected to lateral loads[J]. International Journal of Civil Engineering, 2019, 17(3): 397-426. DOI:10.1007/s40999-018-0366-0 |
| [13] |
Chen W,Xiong F,Lu Y,et al. Experimental investigation of the seismic performance of a novel bolt-assembled precast panel building structure[J]. Journal of Earthquake and Tsunami, 2019, 13(3n04): 1940008. DOI:10.1142/s1793431119400086 |
| [14] |
Guo Wei,Zhai Zhipeng,Cui Yao,et al. Seismic performance assessment of low-rise precast wall panel structure with bolt connections[J]. Engineering Structures, 2019, 181: 562-578. DOI:10.1016/j.engstruct.2018.12.060 |
| [15] |
Sun Jian,Qiu Hongxing,Jiang Hongbo. Experimental study and associated mechanism analysis of horizontal bolted connections involved in a precast concrete shear wall system[J]. Structural Concrete, 2019, 20(1): 282-295. DOI:10.1002/suco.201800113 |
| [16] |
Xu Yong.Dry connections for precast shear wall in rural housing[D].Chengdu:Sichuan University,2017. 徐咏.装配式墙板农居结构干式节点性能研究[D].成都:四川大学,2017. |
| [17] |
Wang Wei,Xiong Feng,Xu Jinxiang,et al. Experimental study on shear behavior of the bolt connection of prefabricated concrete wallboard[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(Supp2): 86-92. [王威,熊峰,徐锦祥,等. 预制装配式混凝土墙板螺栓连接抗剪性能试验研究[J]. 四川大学学报(工程科学版), 2016, 48(增刊2): 86-92. DOI:10.15961/j.jsuese.2016.s2.014] |
| [18] |
Chen Wen,Xiong Feng,Chen Jiang,et al. Experimental study on seismic behavior of prefabricated panel structure by dry connectors[J]. Journal of Building Structures, 2018, 39(10): 56-64. [陈文,熊峰,陈江,等. 干式连接装配式墙体结构抗震性能试验研究[J]. 建筑结构学报, 2018, 39(10): 56-64. DOI:10.14006/j.jzjgxb.2018.10.007] |
| [19] |
Vidjeapriya R,Jaya K P. Experimental study on two simple mechanical precast beam-column connections under reverse cyclic loading[J]. Journal of Performance of Constructed Facilities, 2013, 27(4): 402-414. DOI:10.1061/(asce)cf.1943-5509.0000324 |
| [20] |
Park R. Evaluation of ductility of structures and structural assemblages from laboratory testing[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 1989, 22(3): 155-166. DOI:10.5459/bnzsee.22.3.155-166 |
| [21] |
中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S].北京:中国建筑工业出版社,2011.
|
| [22] |
中华人民共和国住房和城乡建设部.钢结构设计标准:GB 50017—2017[S].北京:中国建筑工业出版社,2017.
|
 2022, Vol. 54
2022, Vol. 54


