2. 四川大学 水力学与山区河流开发保护国家重点实验室,四川 成都 610065
2. State Key Lab. of Hydraulics and Mountain River Eng., Chengdu 610065, China
由堆积碎石层组成的坡体广泛存在于中国各地,若受工程活动或自然影响致滑成灾,往往会造成巨大的经济损失和人员伤亡。如:2001年,西藏昌都芒康县由于岩土体冻胀融缩、风蚀干燥引发山体出现持续的崩塌碎屑流现象;2010年,贵州关岭县岗乌镇大寨村发生特大型崩滑碎屑(石)流灾害,造成99人死亡失踪;2013年,西藏墨竹工卡县泽日山东坡发生滑坡碎屑流,造成83人死亡失踪[1]。这种崩滑产生的滑坡碎屑流的宏观力学性质与降雨导致的泥石夹杂的滑坡泥石流差异较大。由于泥的黏结作用,泥石流通常存在较大的黏聚力,而碎屑流可视为没有黏聚力的大量堆积碎石类材料在重力作用下的滚落滑动。研究这类堆积碎石材料的力学性质,可增加对滑坡碎屑流等自然灾害的认识,从而对这类灾害进行更有效的预防治理。
在堆积碎石类材料的力学特性研究方面,相关领域学者现阶段主要从现场试验[2-3]和数值模拟[4-7]两个方面进行。由于现场试验费用昂贵且实施复杂,大量的试验研究在时间和资源上的投入成本较大,因此,结合数值模拟揭示堆积碎石类材料相关力学特性也成为一种主要的研究手段。PFC是一种成熟的商用颗粒离散元计算软件,广泛运用于岩土工程、灾害治理等诸多领域。如:Utili等[8]提出一种基于Morh–Coulomb准则的离散元接触模型,模拟了边坡的破坏过程;Wang等[9]利用PFC2D对节理岩体边坡进行了稳定性分析;Hadjigeorgiou等[10]在PFC3D中引入裂缝系统并研究了硬岩中垂直开挖的边坡稳定性。PFC利用牛顿三定律和应力–应变法则确定各颗粒间的接触力及运动方式,颗粒间的接触特性,即接触本构及其参数值决定了颗粒材料的宏观力学性质[11-12];而接触本构由接触刚度、摩擦系数、阻尼等细观参数描述,只有正确标定细观参数,才能保证离散介质数值模拟结果的科学性和可靠性。
由于岩土材料的宏观、细观参数众多,故细观参数的标定工作难度较大,许多学者基于室内压缩试验开展岩石介质的细观参数标定工作,如:Chen等[13]基于岩石三轴压缩试验,利用试错法标定了岩样的细观力学参数,对含微裂纹的岩石压缩和拉伸力学行为进行了研究;Shi等[14]基于岩石单轴压缩试验,提出一套岩石细观参数的标定流程,并根据室内试验模拟了花岗岩的力学行为;Yoon[15]基于单轴压缩试验,提出一种利用筛选试验设计和中心组合设计的细观参数标定优化方法。但是,目前离散元方法中的细观参数标定方法研究主要聚焦于岩石材料,对于滑坡碎屑流等颗粒介质的细观参数标定方法缺乏系统性研究。在目前主流滑坡离散元数值模拟中,细观参数均按经验进行取值[16-18],忽略了岩土材料宏–细观参数联系;且不同滑坡体材料具有独特的物理力学特性,其细观参数必然显著不同,按经验或类比对细观参数取值不利于对滑坡碎屑流灾害进行正确模拟。因此亟待提出能够快速、正确地标定堆积碎石类材料细观参数的方法。
相较于三轴压缩试验,直剪试验具有设备轻便、操作简单、省时节材的优点,对于现场环境有更好的适应性。结合室内堆积碎石直剪试验,采用PFC3D软件建立等尺度3维数值模型,基于线性模型揭示堆积碎石宏–细观力学参数之间的关系,提出堆积碎石类材料细观参数的系统性标定方法;基于此,研究直剪过程中堆积碎石的剪切力学特性并开展堆积碎石的滑坡模拟试验,以验证本文的细观参数标定方法在堆积碎石类材料滑坡分析中的适用性及合理性。
1 堆积碎石直剪试验本文采用堆积碎石开展3组重复直剪试验,试样如图1所示,呈平均长宽比为1.4(随机20粒测量均值)的不规则粒状;使用标准筛进行筛分,其粒径分布集中于两个粒径范围,见表1 ,相关物理参数也列于表1,其中,粒间摩擦系数取该堆积碎石试样自然休止角的正切值[19];用于直剪试验的直剪盒如图2所示。
 |
| 图1 直剪试验堆积碎石试样 Fig. 1 Accumulated debris in direct shear test |
| 表1 堆积碎石物理参数 Tab. 1 Physical parameters of accumulated debris |
 |
 |
| 图2 直剪盒 Fig. 2 Direct shear box |
直剪试验中,为消除颗粒之间的间隙或无效接触,首先,采用100 kPa的法向力对堆积碎石散粒进行预压;然后,对试样进行200、300、400 kPa的逐级法向加载,并记录相应荷载下的位移值;之后,在400 kPa的法向荷载作用下进行土样直剪试验,剪切速度为0.8 mm/min。
法向荷载施加过程中,试件法向应力与法向位移之间的关系曲线如图3(a)所示,法向应力与法向位移之间近似呈线性正相关,试样承受的法向荷载越大,其法向位移也越大。剪切过程中,剪应力与剪位移之间的关系曲线如图3(b)所示,剪应力随剪切位移的增大而增大,但增长速率逐渐减小。
 |
| 图3 室内直剪试验结果 Fig. 3 Results of indoor direct shear test |
2 直剪试验宏细观参数关系
为正确把握细观参数对于宏观性质的影响,以合理提出堆积碎石细观参数标定方法,建立直剪试验离散元数值模型,并对直剪试验中的宏细观参数关系进行探究。
2.1 直剪离散元模型基于堆积碎石室内直剪试验开展等尺寸的数值模拟。剪切盒模型尺寸大小为(直径×高)61.82 mm×45.75 mm,上下盒等高,模型周围由刚性墙组成边界,模拟直剪盒的侧向约束作用。剪切时,下盒固定不动,上盒水平向右错动进行剪切,如图4所示。
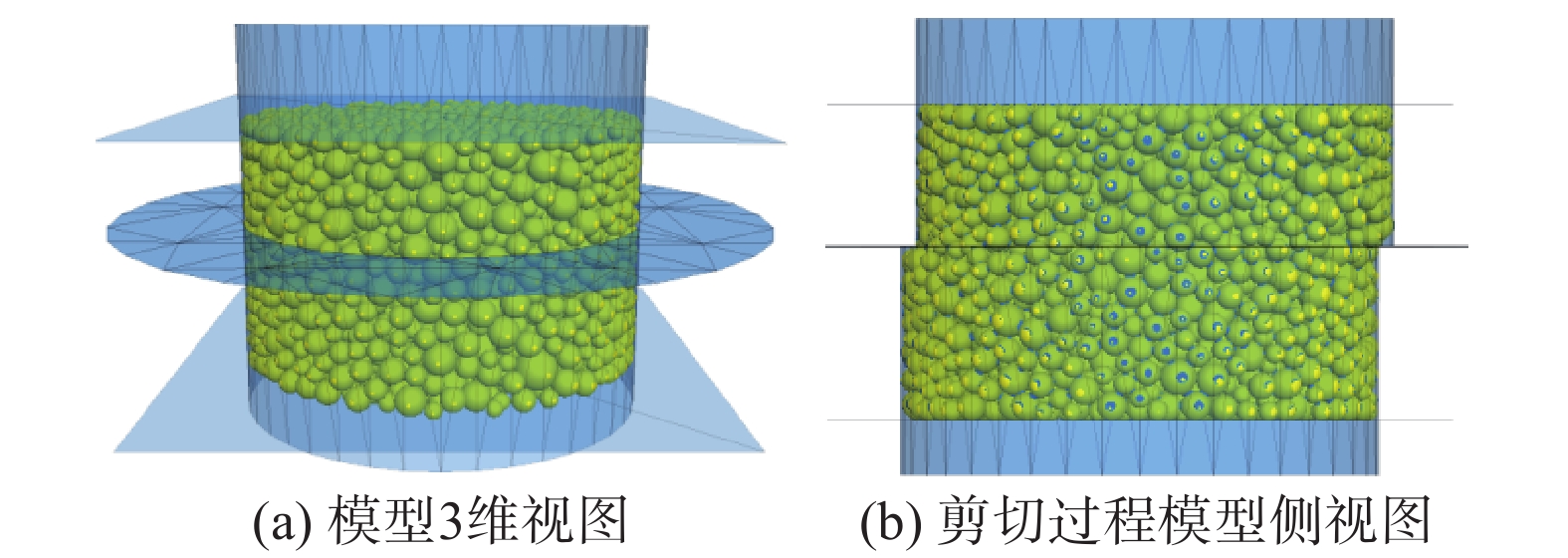 |
| 图4 3维离散元数值模型 Fig. 4 Three dimensional discrete element numerical model |
实际堆积碎石为不规则状,数值模拟采用与实际试样相同级配的球形颗粒进行等效模拟;进行合理的细观参数取值后,堆积碎石组的数值模拟宏观力学性质能较好地与实际吻合。根据室内试验试样的颗粒级配,在剪切盒内部生成与实际级配相匹配的球形颗粒。颗粒间的相对密度为2.79 g/cm3,粒间摩擦系数为0.735。
对于堆积碎石这类粒间无黏性、有摩擦的颗粒材料,线性模型是最适用的接触本构[20],故本文的数值模拟采用线性模型,各细观参数见表2。
| 表2 数值模拟细观参数 Tab. 2 Mesoscopic parameters in numerical simulation |
 |
直剪数值模拟过程与室内直剪试验一致,在线性模型中,所涉及的接触参数均与时间无关,剪切速率对直剪试验宏观力学性质的影响不大,这一点已由刘方成等[21]等进行了计算论证。因此,为提高计算效率,数值模拟中在逐级施加法向荷载后,采用2 mm/s的剪切速率进行碎石颗粒的剪切试验。
2.2 接触刚度对宏观弹性常数的影响为了从堆积碎石的宏观力学响应出发确定粒间接触刚度kn、ks,基于室内直剪试验结果,采用Kn和Ks两个宏观力学参数表征试样的弹性变形。其中,Kn为法向荷载施加过程中法向应力–法向位移曲线的斜率,Ks为剪切过程中剪应力–剪位移曲线弹性段(近直线段)的斜率。故可建立如式(1)所示的细–宏观弹性常数关系:
| $ \left\{ \begin{gathered} {K_{\rm{n}}} = f({k_{\rm{n}}},{k_{\rm{s}}}),\hfill \\ \hfill \\ {K_{\rm{s}}} = g({k_{\rm{n}}},{k_{\rm{s}}}) \hfill \\ \end{gathered} \right. $ | (1) |
为揭示颗粒接触刚度与直剪试样宏观弹性常数的内在联系,基于不同的kn和ks开展多组直剪数值模拟。图5和6为不同切向接触刚度ks条件下,试件宏观弹性常数Kn、Ks与kn之间的拟合关系曲线。
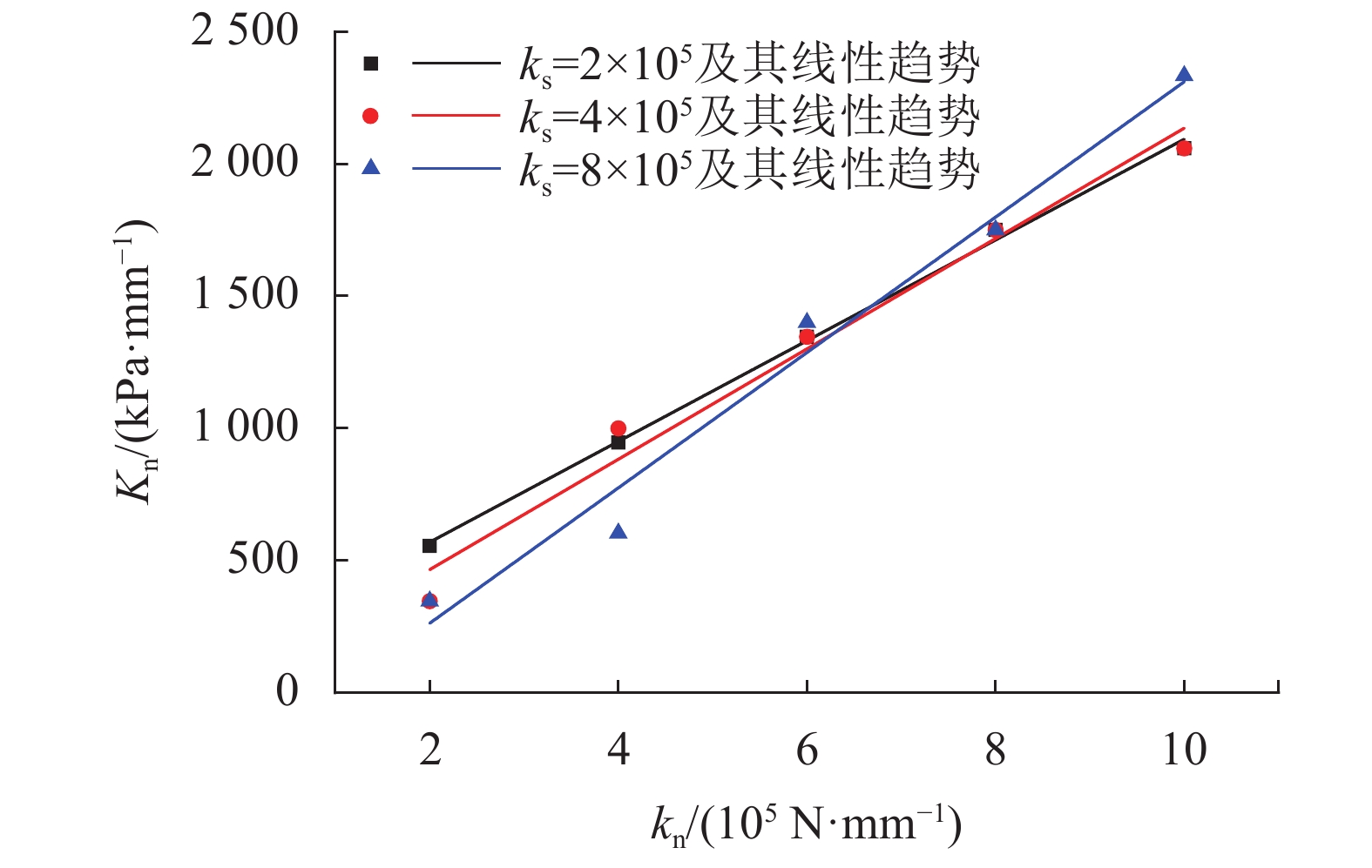 |
| 图5 不同ks下Kn–kn线性趋势曲线 Fig. 5 Linear trend curves of the relationship between Kn and kn under different ks |
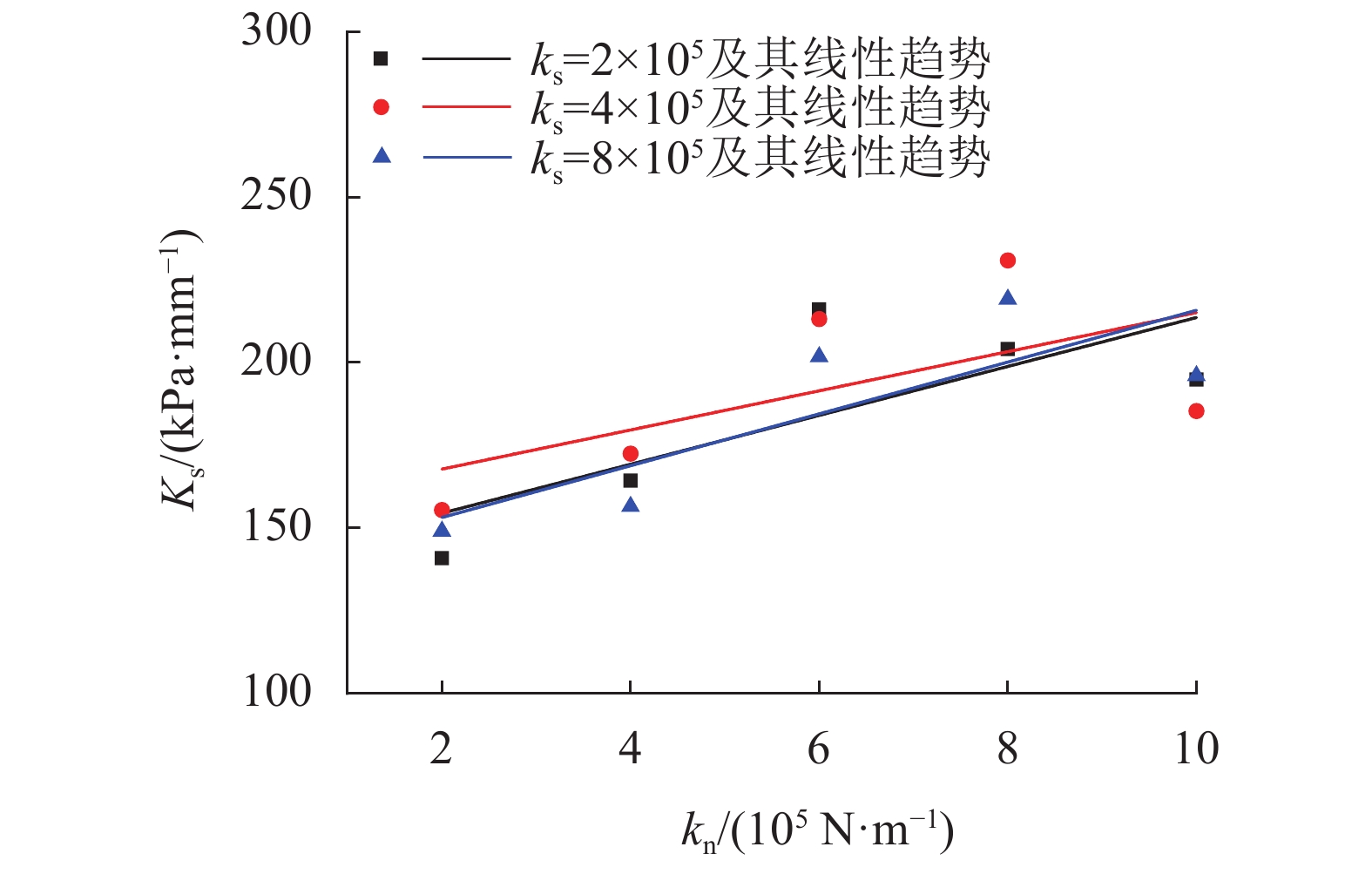 |
| 图6 不同ks下Ks–kn线性趋势曲线 Fig. 6 Linear trend curves of the relationship between Ks and kn under different ks |
由图5和6可知,在切向接触刚度ks不变情况下,随着法向接触刚度kn增大,宏观弹性常数Kn、Ks随之增大,但Kn随法向接触刚度kn增大的变化率较大。
图7和8为不同法向接触刚度kn条件下,试样宏观弹性常数Kn、Ks与切向接触刚度ks之间的拟合关系曲线。由图7和8可知,法向刚度Kn、切向刚度Ks与切向接触刚度ks的直线拟合关系近似一条水平线,切向接触刚度ks对Kn、Ks的影响相对较小。由此可知,试样宏观弹性常数Kn和Ks主要受粒间法向接触刚度kn的影响,而受粒间切向接触刚度ks的影响相对较小。
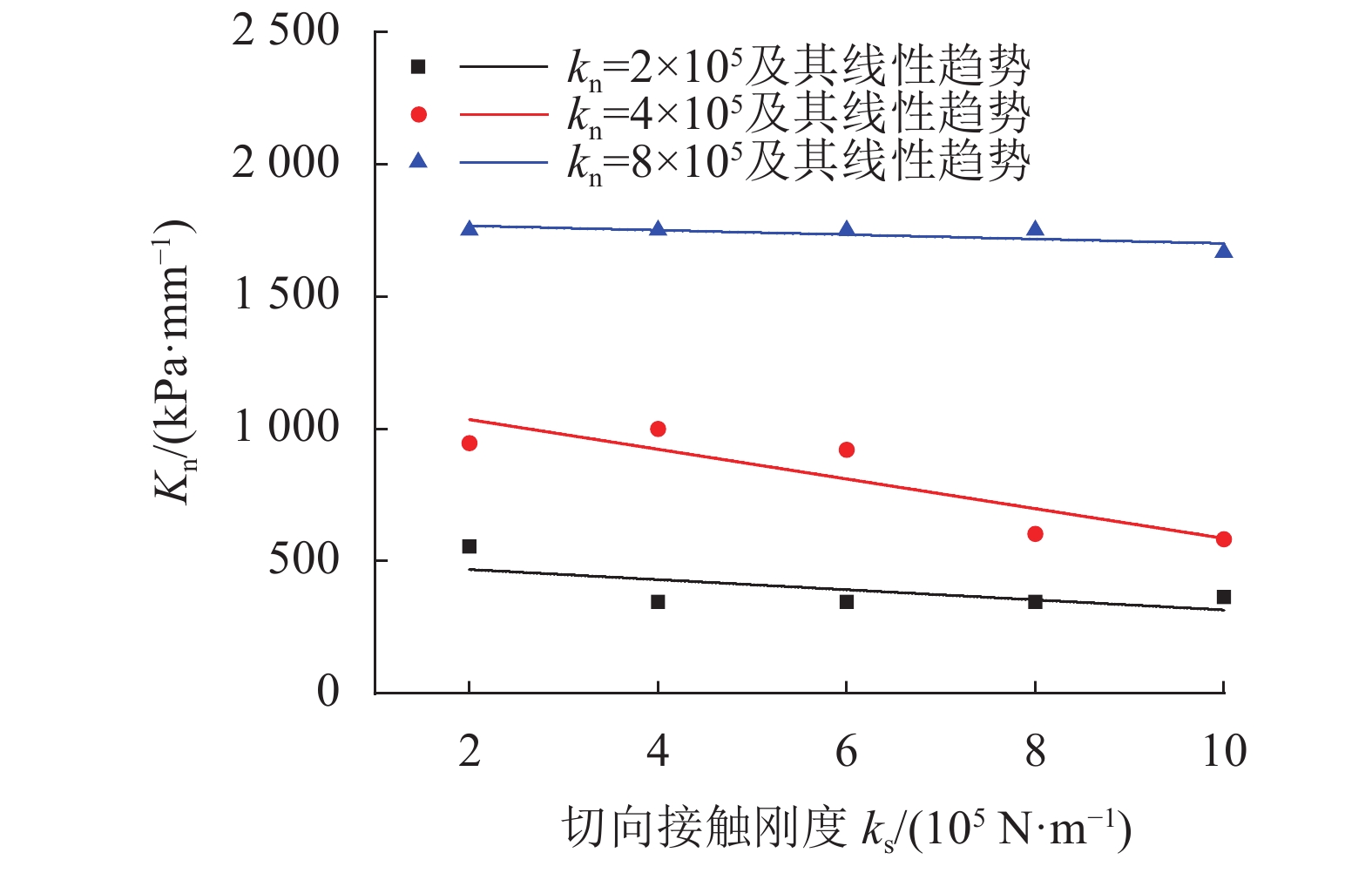 |
| 图7 不同kn下Kn–ks线性趋势曲线 Fig. 7 Linear trend curves of the relationship between Kn and ks under different kn |
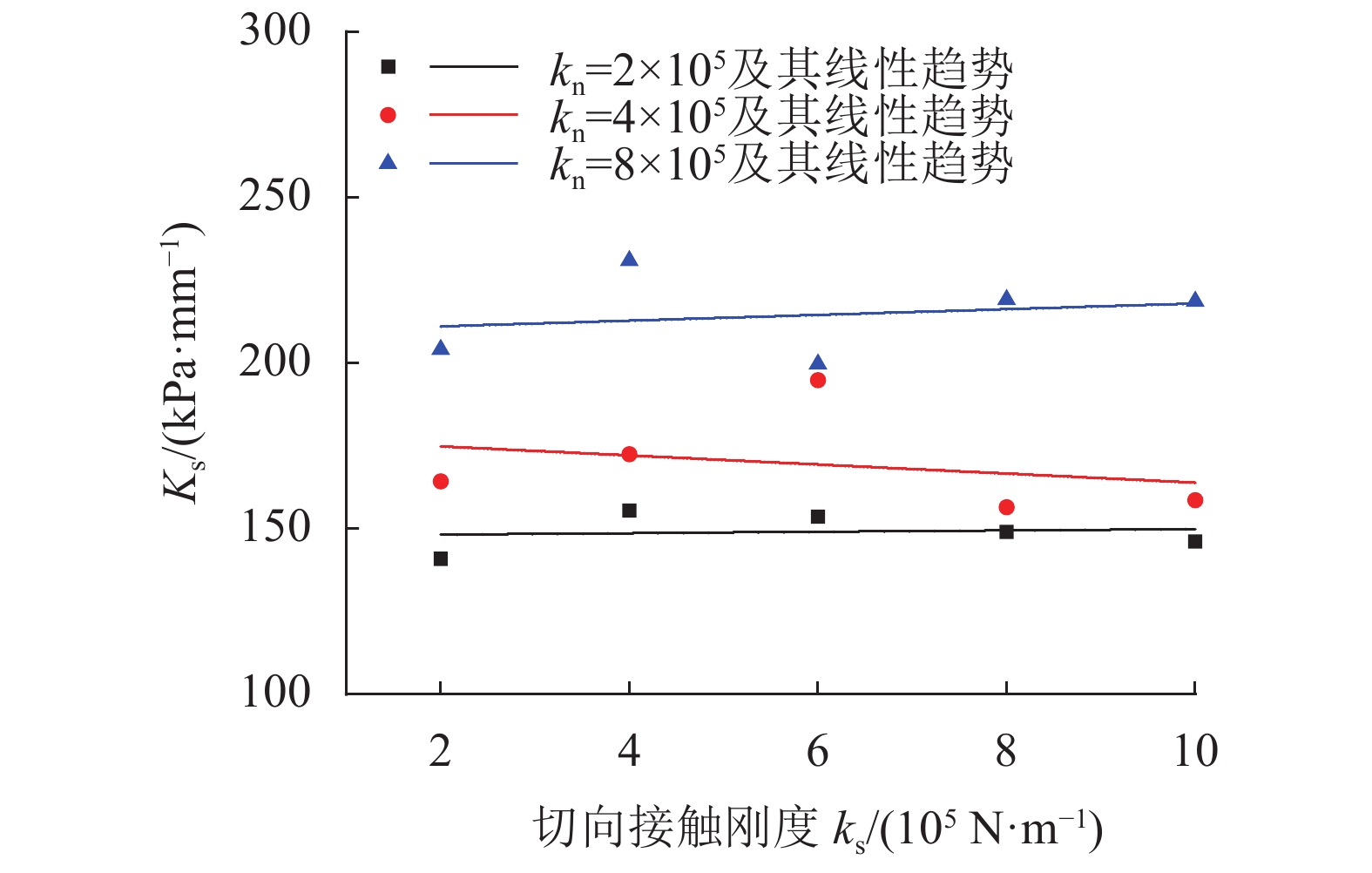 |
| 图8 不同kn下Ks–ks线性趋势曲线 Fig. 8 Linear trend curves of the relationship between Ks and ks under different kn |
综上可知:堆积碎石试样的宏观弹性常数Kn及Ks均主要受颗粒间法向接触刚度kn的影响;切向接触刚度ks对于其宏观力学性质的影响远不及kn。故在一定的切向接触刚度范围内,可忽略ks变化对堆积碎石试样宏观弹性常数的影响,可将ks作为常量,或者将ks与kn通过一定关系联系起来使式(1)只存在唯一变量kn,即简化为:
| $ \left\{ \begin{gathered} {K_{\rm{n}}} = f({k_{\rm{n}}}), \hfill \\ \hfill \\ {K_{\rm{s}}} = g({k_{\rm{n}}}) \hfill \\ \end{gathered} \right. $ | (2) |
由图5可知,Kn与kn呈现明显的线性相关关系,可假设Kn由kn的线性单增函数表示;由图6可知,Ks总体呈现随kn增加而增速减缓、略有波动的增加模式,可假设Ks由kn的斜率减小的非线性单增函数表示;又考虑到各常数的物理意义,当kn = 0时,有Kn= 0、Ks = 0,故式(2)可表述为:
| $ \left\{ \begin{gathered} {K_{\rm{n}}} = a \times {k_{\rm{n}}}, \hfill \\ \hfill \\ {K_{\rm{s}}} = {{b}} \times \ln (c \times {k_{\rm{n}}} + 1) \hfill \\ \end{gathered} \right. $ | (3) |
式中,a、b、c均为常数。
3 细观参数的标定方法基于前文,提出一种堆积碎石细观参数标定方法,步骤如下:
1)进行堆积碎石室内直剪试验,得到试验法向位移–法向应力曲线、剪位移–剪应力曲线。
2)通过试验手段测得碎石颗粒试样级配、孔隙率、密度、摩擦系数,作为直剪试验数值模拟建模计算的基础参数,本文参数如表2所示。
3)建立直剪数值模型,通过试算确定刚度比k*(kn/ks),通常取1~3[22];收敛原则为随着kn的增加,Kn、Ks总体呈增加趋势且无较大波动,本文取k*=1.25。
4)以kn为变量,开展多次数值模拟,计算并拟合得出宏观弹性常数Kn、Ks分别与kn之间的经验公式。
5)分别以Kn、Ks试验值反演得到法向接触刚度kn(n) 、kn(s);若两者相差较小(10%),则标定成功,kn取kn(n)、kn(s)的均值即可;若两者相差较大,则需调整刚度比k*,重新标定。
标定流程如图9所示。
 |
| 图9 细观参数标定流程 Fig. 9 Flow of mesoscopic parameters calibration method |
利用此标定方法对本文所用堆积碎石进行细观参数标定,步骤1)、2)在第2节已完成,步骤3)、4)、5)的具体过程如下。
图10、11分别为数值模拟刚度比k*=1.25时的Kn、Ks与法向接触刚度kn之间的拟合关系曲线,拟合公式为:
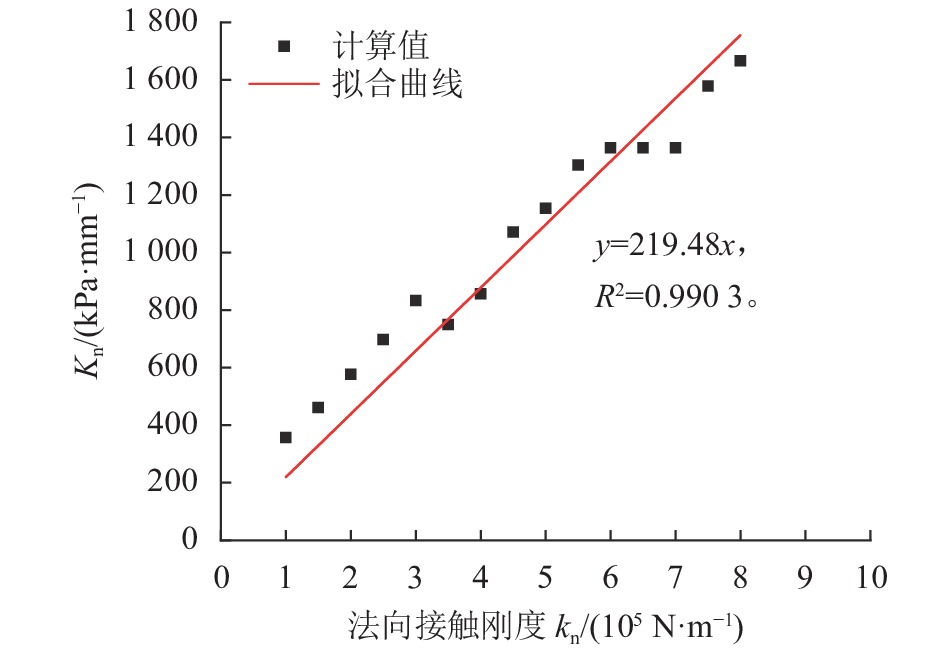 |
| 图10 k*=1.25时Kn–kn拟合关系曲线 Fig. 10 Fittng curve of the relationship between Kn and kn when k*=1.25 |
 |
| 图11 k*=1.25时Ks–kn拟合关系曲线 Fig. 11 Fittng curve of the relationship between Ks and kn when k*=1.25 |
| $ \left\{ \begin{gathered} {K_{\rm{n}}} = 219.48{k_{\rm{n}}}, \hfill \\ {K_{\rm{s}}} = {\text{89}}{\text{.0}}\ln (5.25{k_{\rm{n}}} + 1) \hfill \\ \end{gathered} \right. $ | (4) |
对3次室内试验结果(图3)取平均值计算可得,堆积碎石的直剪宏观弹性常数分别为Kn=501.39 kPa/mm、Ks=229.27 kPa/mm。根据式(4)可反演得到粒间法向接触刚度kn(n)=2.283 1×105 N/m、kn(s) =2.313 2×105 N/m,两拟合公式所标定的法向接触刚度kn相差不大,进一步说明在颗粒材料直剪试验中宏观力学参数Kn、Ks对粒间切向接触刚度ks的变化不敏感。本文取kn(n)、kn(s)的均值作为粒间切向接触刚度的标定值,即kn=2.3×105 N/m。
4 室内直剪试验的数值模拟以表2的细观参数及标定后的接触刚度kn= 2.3×105 N/m、ks= 1.84×105 N/m(按k*=1.25取值)为最终参数,进行堆积碎石直剪试验数值模拟计算,监测并记录试样的位移与应力变化,同时对试样直剪过程中的剪切特性进行研究。
4.1 数值模拟结果及分析图12为数值模拟与室内试验的法向应力–法向位移曲线对比。由图12可知,Kn模拟值较试验值大,偏差为21.4%,其原因是室内试验的碎石颗粒为不规则颗粒且其棱角的细部结构在压密过程中存在破碎,其粒间空间更易受外力荷载的扰动,故实际不规则颗粒粒间空隙较数值模拟纯圆颗粒更易压密。
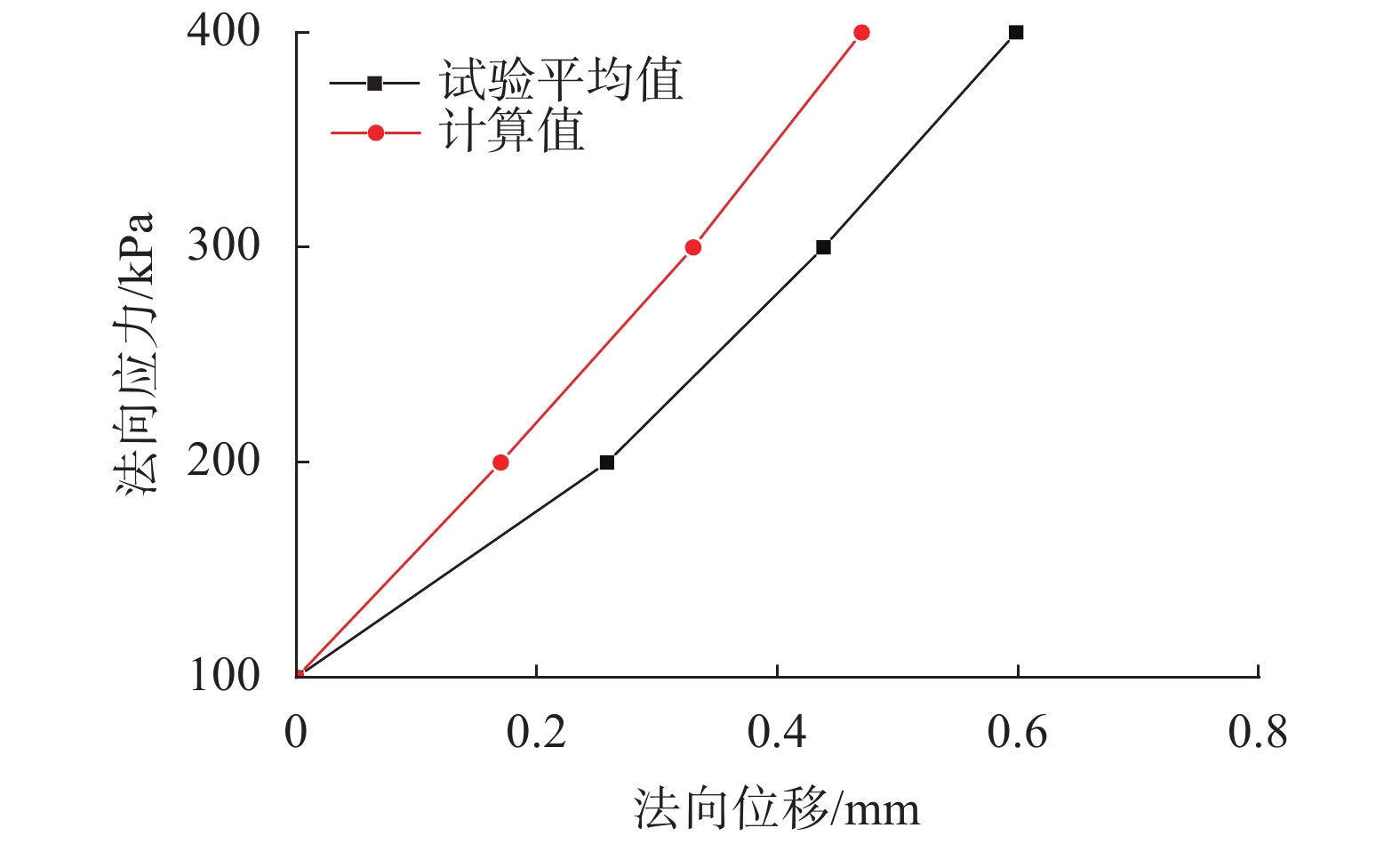 |
| 图12 数值模拟与室内试验法向应力–法向位移曲线对比 Fig. 12 Comparison of normal stress–normal displacement curves between numerical simulation and laboratory test |
图13为数值模拟与室内试验的剪应力–剪位移曲线对比。由图13可知:除了弹性阶段的剪切过程,Ks模拟值与试验值基本一致;并且,在剪切过程中的塑性阶段,模拟值也与试验值吻合度较高,证明了本文堆积碎石直剪试验数值模拟细观参数标定方法的合理性及可行性。
 |
| 图13 数值模拟与室内试验的剪应力–剪位移曲线对比 Fig. 13 Comparison of shear stress–shear displacement curves between numerical simulation and laboratory test |
4.2 颗粒接触力链网络研究
颗粒体系内部的接触互相连接逐渐形成能够传递荷载的通道,即力链,这些通道错综复杂地交织,形成力链网络[23]。本文针对直剪试验数值模拟中的力链网络演变,从微观层面研究直剪过程中碎石骨架受力情况。
图14为在400 kPa法向荷载作用下,剪切过程中试样内部的力链网络演变过程。由图14(a)可知,试样剪切前的力链网络强力链较少,且强力链方向受法向荷载影响呈竖向分布的特征。在剪切初期,随着上部剪切盒向右运动带动试样剪切变形,力链网络发生重构,强力链数量开始增加且力链方向开始倾斜,如图14(b)所示。由图14(c)可见,随着剪位移的增加,强力链显著沿对角线方向聚集,试样左下方及右上方几乎没有强力链分布。研究表明,随着剪切位移的增加,力链网络中强力链数量随之增加,强力链分布由竖直方向逐渐向对角线方向演变,而剪应力也随着强力链数量增加和方向偏转而增大。
 |
| 图14 试样内部力链网络演变 Fig. 14 Evolution of force chain network in specimen |
4.3 剪胀性与颗粒速度场研究
图15为剪切过程中试样的体积变化率–剪位移曲线及不同阶段试样颗粒速度场。由图15可知:试样剪胀性与颗粒速度场之间存在着密切联系;在曲线点A处,法向加载施加完成,但试样还未开始剪切,体积变化率为0,颗粒速度场杂乱分布;在曲线点B处,试样正处于剪缩阶段,从颗粒速度场也可见颗粒从剪切盒左上方向右下方挤压,上部颗粒整体从左往右运动的趋势,故颗粒间彼此贴紧,体积有收缩趋势;随着剪切的进行,位移增大至曲线点C时,试样处于回胀阶段,从颗粒速度场可见,除左下角外,颗粒体系的整体运动趋势为斜向右上运动,此时由于颗粒间咬合摩擦,造成颗粒跨越而产生相对错动,故体积有膨胀趋势。
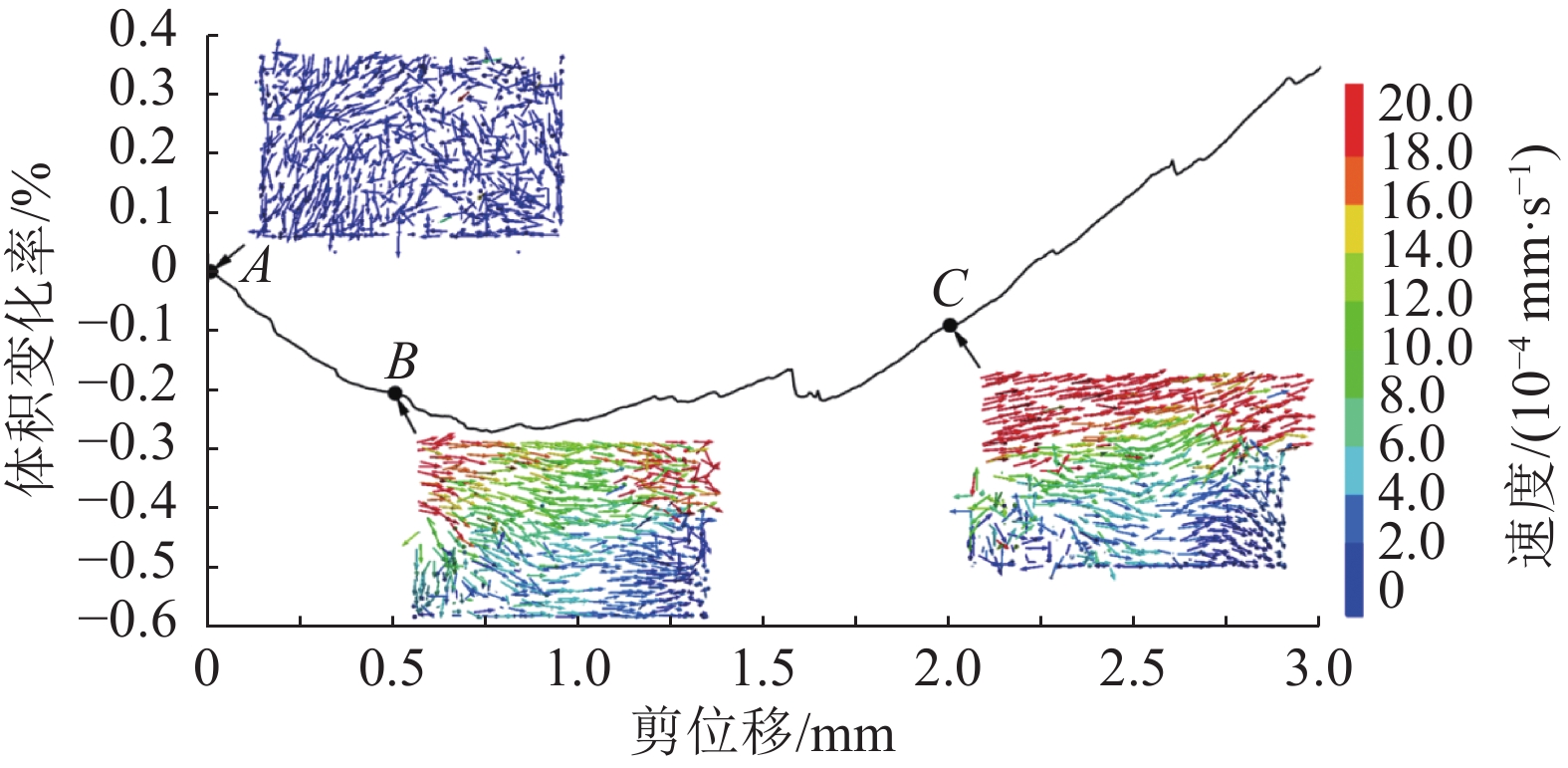 |
| 图15 试样体积变化率–剪位移曲线及特征时刻试样速度场 Fig. 15 Curve of volume change rate-shear displacement and velocity field of specimen at specific time |
5 堆积碎石滑坡模拟试验
为进一步验证本文细观参数标定在堆积碎石滑坡分析时的适用性,进行堆积碎石滑坡模拟试验并进行数值模拟对比。试验滑槽模型如图16所示,室内试验采用的碎石材料与图1中材料一致,重200 g;滑坡数值模拟的颗粒为圆球形,其级配、摩擦系数、密度、接触刚度等各参数均与上文直剪试验数值模拟所确定的参数一致。
 |
| 图16 滑坡模拟试验滑槽模型 Fig. 16 Slide model of landslide simulation test |
试验时,以挡板将碎石颗粒组挡在滑槽中离地高度20 cm处,随即释放挡板,使碎石组沿滑槽自由下滑至堆积槽内堆积成型。数值模拟过程与室内试验保持完全一致。
碎石滑坡堆积形态对比如图17所示。由图17(a)可以看出:室内试验及数值模拟结果的俯视堆积形态均近似呈半椭圆形,椭圆中心均在远离滑板一侧的立板中轴线上,短半轴均为堆积槽宽度(10 cm);但是,数值模拟结果的长轴为24.0 cm,较实际的22.5 cm偏宽,相差6.67%。由图17(b)可以看出:室内试验及数值模拟结果的正视堆积形态均近似呈正态分布,峰值点均位于滑槽中心线上,数值模拟与室内试验最大堆积高度分别为2.3、2.7 cm,相差14.8%;通过轮廓线对比可以看出,数值模拟堆积高度整体较实际偏低。由图17(c)可以看出:室内试验及数值模拟的侧视堆积形态均近似呈半正态分布,远离滑板一侧为最高点;通过轮廓线对比可以看出,左侧部分数值模拟与实际拟合良好,右侧部分数值模拟结果较实际偏低。
 |
| 图17 碎石堆积形态对比 Fig. 17 Comparison of gravel accumulated morphology |
分析认为,数值模拟所得碎石堆积形态与室内试验基本一致,但数值模拟的堆积范围较实际偏大(6.67%),堆积高度较实际偏低(14.8%)。这些误差是由数值模拟采用的球型颗粒较实际不规则颗粒更易滚动所导致的。数值模拟的滑坡体外轮廓线与室内试验整体吻合较好,进一步验证了本文细观参数标定在模拟堆积碎石滑坡时的适用性。
6 结论与展望基于线性接触模型开展堆积碎石直剪试验,揭示了宏观力学性质与粒间细观接触参数之间的相关关系,提出颗粒材料细观参数标定方法并进行验证,主要结论如下:
1)在碎石直剪数模试验中,碎石的宏观弹性参数主要受粒间法向接触刚度kn的影响,受粒间切向接触刚度ks的影响相对较小。
2)提出一种基于室内直剪试验的堆积碎石细观参数标定方法,该方法利用两个弹性常数对细观参数进行标定,操作简便,耗材耗时均较小,可重复性高;并通过直剪试验数值模拟与室内试验对比验证了该方法的适用性和准确性。
3)通过直剪数模试验分析了碎石剪切过程中颗粒粒间力链网络演变过程,随着剪位移和剪应力的增加,力链网络中的强力链数量增加,且强力链分布由竖直方向逐渐向对角线方向偏转。
4)土样在剪切过程中,颗粒速度场由最初的杂乱分布,逐渐呈现斜向下近似水平的运动趋势,颗粒间彼此贴紧,体积收缩;随着剪切位移的增大,颗粒间咬合摩擦造成颗粒跨越而产生相对错动,速度场呈现斜向上运动趋势,发生剪胀现象。
5)通过本文直剪试验细观参数标定方法所得到的堆积碎石细观参数,可较好地应用于滑坡堆积碎石的数值模拟,其模拟堆积形态、堆积范围均与实际相符。
| [1] |
Liu Chuanzheng. Genetic types of landslide and debris flow disasters in China[J]. Geological Review, 2014, 60(4): 858-868. [刘传正. 中国崩塌滑坡泥石流灾害成因类型[J]. 地质论评, 2014, 60(4): 858-868. DOI:10.3969/j.issn.0371-5736.2014.04.015] |
| [2] |
Pan Jiajun,Cheng Zhanlin,Yu Ting,et al. Experimental study on stress-strain characteristics of coarse-grained soil under different intermediate principal stresses[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(11): 2078-2084. [潘家军,程展林,余挺,等. 不同中主应力条件下粗粒土应力变形特性试验研究[J]. 岩土工程学报, 2016, 38(11): 2078-2084. DOI:10.11779/CJGE201611018] |
| [3] |
Ding Yanhui,Zhang Bingyin,Qian Xiaoxiang,et al. Experimental study of the characteristics of wetting deformation of rockfill materials[J]. Rock and Soil Mechanics, 2019, 40(8): 2975-2981. [丁艳辉,张丙印,钱晓翔,等. 堆石料湿化变形特性试验研究[J]. 岩土力学, 2019, 40(8): 2975-2981. DOI:10.16285/j.rsm.2018.0891] |
| [4] |
Jia Xueming,Chai Hejun,Zheng Yingren. Mesomechanics research of large direct shear test on soil and rock aggregate mixture with particle flow code simulation[J]. Rock and Soil Mechanics, 2010, 31(9): 2695-2703. [贾学明,柴贺军,郑颖人. 土石混合料大型直剪试验的颗粒离散元细观力学模拟研究[J]. 岩土力学, 2010, 31(9): 2695-2703. DOI:10.3969/j.issn.1000-7598.2010.09.002] |
| [5] |
Ma Shicheng,Hu Junxia,Ma Yiyue,et al. Research on mesoscopic-macroscopic mechanical parameters correlation of accumulation of gravel soil based on three dimensional discrete element[J]. Chinese Journal of Computational Mechanics, 2016, 33(1): 73-82. [马石城,胡军霞,马一跃,等. 基于三维离散元堆积碎石土细–宏观力学参数相关性研究[J]. 计算力学学报, 2016, 33(1): 73-82. DOI:10.7511/jslx201601012] |
| [6] |
Xu Wenjie,Wang Shi. Meso-mechanics of soil-rock mixture with real shape of rock blocks based on 3D numerical direct shear test[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(10): 2152-2160. [徐文杰,王识. 基于真实块石形态的土石混合体细观力学三维数值直剪试验研究[J]. 岩石力学与工程学报, 2016, 35(10): 2152-2160. DOI:10.13722/j.cnki.jrme.2015.0927] |
| [7] |
Wang Zihan,Wang Pengju,Jing Xiaokun,et al. A study on inter-particle contact behaviors and micro contact models of coarse-grained soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(8): 1980-1992. [王子寒,王鹏举,景晓昆,等. 粗粒土颗粒接触力学特性及细观接触模型研究[J]. 岩石力学与工程学报, 2018, 37(8): 1980-1992. DOI:10.13722/j.cnki.jrme.2017.1657] |
| [8] |
Utili S,Nova R. DEM analysis of bonded granular geomaterials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(17): 1997-2031. DOI:10.1002/nag.728 |
| [9] |
Wang C,Tannant D D,Lilly P A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 415-424. DOI:10.1016/S1365-1609(03)00004-2 |
| [10] |
Hadjigeorgiou J,Esmaieli K,Grenon M. Stability analysis of vertical excavations in hard rock by integrating a fracture system into a PFC model[J]. Tunnelling and Underground Space Technology, 2009, 24(3): 296-308. DOI:10.1016/j.tust.2008.10.002 |
| [11] |
Cundall P A.The art of numerical modeling in geomechanics[C].University-of-Minnesota 68th Annual Geotechnical Engineering Conference (Geo-Congress). Minneapolis,2020.
|
| [12] |
石崇,张强,王盛年.颗粒流(PFC5.0)数值模拟技术及应用[M].北京:中国建筑工业出版社,2018.
|
| [13] |
Chen Xiao,Shi Chong,Ruan Huaining,et al. Numerical simulation for compressive and tensile behaviors of rock with virtual microcracks[J]. Arabian Journal of Geosciences, 2021, 14(10): 870. DOI:10.1007/s12517-021-07163-7 |
| [14] |
Shi Chong,YangWenkun,Yang Junxiong,et al. Calibration of micro-scaled mechanical parameters of granite based on a bonded-particle model with 2D particle flow code[J]. Granular Matter, 2019, 21(2): 38.1-38.13. DOI:10.1007/s10035-019-0889-3 |
| [15] |
Yoon J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(6): 871-889. DOI:10.1016/j.ijrmms.2007.01.004 |
| [16] |
Zhang Long,Tang Huiming,Xiong Chengren,et al. Movement process simulation of high-speed long-distance Jiweishan landslide with PFC3D[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Supp1): 2601-2611. [张龙,唐辉明,熊承仁,等. 鸡尾山高速远程滑坡运动过程PFC3D模拟[J]. 岩石力学与工程学报, 2012, 31(增刊1): 2601-2611. DOI:10.3969/j.issn.1000-6915.2012.z1.002] |
| [17] |
Li Zilong,Wang Lang. Simulation study over river damming of small and medium-sized reservoirs in mountainous area based on PFC2D[J]. Pearl River, 2019, 40(3): 123-127. [李子隆,王浪. 基于PFC2D的山区中小型水库滑坡堵江模拟研究[J]. 人民珠江, 2019, 40(3): 123-127. DOI:10.3969/j.issn.1001-9235.2019.03.021] |
| [18] |
Wu Jianchuan,Zhang Shishu,Wu Shuang,et al. Simulation on accumulation process and form of a barrier dam based on PFC3D[J]. Yangtze River, 2020, 51(4): 135-141. [吴建川,张世殊,吴爽,等. 基于PFC3D的滑坡堰塞坝堆积过程与形态模拟[J]. 人民长江, 2020, 51(4): 135-141. DOI:10.16232/j.cnki.1001-4179.2020.04.022] |
| [19] |
Montanari D,Agostini A,Bonini M,et al. The use of empirical methods for testing granular materials in analogue modelling[J]. Materials, 2017, 10(6): 635. DOI:10.3390/ma10060635 |
| [20] |
Cundall P A,Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [21] |
Liu Fangcheng,Wu Mengtao. Micromechanics simulation of direct shear test of rubber-sand mixture with discrete element method[J]. Journal of Hefei University of Tecnology, 2017, 40(7): 944-951. [刘方成,吴孟桃. 橡胶砂直剪试验的颗粒离散元细观力学模拟[J]. 合肥工业大学学报( 自然科学版), 2017, 40(7): 944-951. DOI:10.3969/j.issn.1003-5060.2017.07.017] |
| [22] |
Yang Sheng,Li Xiaoqing. Simulation analysis of large direct shear test of soil and rock mixture based on PFC3D[J]. Advanced Engineering Sciences, 2020, 52(3): 78-85. [杨升,李晓庆. 基于3维离散元颗粒流的土石混合体大型直剪试验模拟分析[J]. 工程科学与技术, 2020, 52(3): 78-85. DOI:10.15961/j.jsuese.201900111] |
| [23] |
Sun Qicheng,Xin Haili,Liu Jianguo,et al. Skeleton and force chain network in static granular material[J]. Rock and Soil Mechanics, 2009, 30(Supp1): 83-87. [孙其诚,辛海丽,刘建国,等. 颗粒体系中的骨架及力链网络[J]. 岩土力学, 2009, 30(增刊1): 83-87. DOI:10.3969/j.issn.1000-7598.2009.z1.018] |
 2022, Vol. 54
2022, Vol. 54


