2. 东华理工大学 地球科学学院,江西 南昌 330013;
3. 南昌大学 建筑工程学院,江西 南昌 330000
2. Faculty of Earth Sciences, East China Univ. of Technol., Nanchang 330013, China;
3. School of Civil Eng. and Architecture, Nanchang Univ., Nanchang 330000, China
山体滑坡作为常见的地质灾害,严重威胁着中国人民的生命及财产安全。在提取区域滑坡编录信息及环境因子信息的基础上构建滑坡易发性预测模型并开展易发性分级制图,是滑坡灾害防治的重要技术手段[1]。研究表明,基于机器学习(machine learning,ML)的滑坡易发性预测模型的精度显著高于知识驱动和常规数理统计模型[2-3]。其中,采用监督学习方式的ML模型预测滑坡易发性的本质可被理解为是在滑坡环境因子的基础上利用“历史滑坡”正样本和“非滑坡”负样本的监督分类过程。Zhu等[4]认为负样本的存在有助于克服模型的过拟合现象,是滑坡易发性预测的必要数据条件。可见,正确合理地选择负样本对提高区域滑坡易发性模型的预测精度和可靠性具有非常重要的影响[4-6]。
目前,国内外学者们对于易发性预测建模中滑坡负样本的选择还没有统一的标准。如:郭子正[7]、吴润泽[8]及徐胜华[9]等直接将滑坡范围外的随机点作为负样本点;Dou等[10]将历史滑坡边界作为缓冲区,在距缓冲区一定距离的研究区随机选取负样本;Kavzoglu等[11]利用高分辨率的谷歌地球影像,解译研究区的河道和沟谷等低坡度地区,并从该区域选取负样本。从低坡度地区选择负样本的方法保证了负样本的稳定性,但却会夸大坡度因子对易发性模型的贡献度,导致滑坡易发性结果可靠性较低。例如:Choi等[12]选用坡度为0的区域作为负样本,其易发性预测结果中坡度因子的贡献度远大于其他因子;缪亚敏等[13]基于Xiao等[14]提出的目标空间外向化采样法,将数据映射到地理空间中,验证所采集滑坡负样本的可靠性。由上述方法可知,目前主要依赖专家主观判断、随机选择或根据某一因子特定属性区选择负样本,导致所选择的滑坡负样本的失稳概率不确定或夸大了部分因子对滑坡的贡献度,即选择的负样本不够准确或不具有广泛的代表性,从而降低了滑坡易发性预测建模的精度和可靠性。
针对易发性预测模型构建时的负样本选择问题,以江西省受滑坡灾害影响较严重的瑞金市为例,利用不需要负样本的信息量(information value,IV)模型,初步计算出研究区内的滑坡易发性,划定极低和低易发区,并在划定区域随机选取负样本,进一步建立信息量–支持向量机(IV–SVM)和信息量–随机森林(IV–RF)的耦合模型开展滑坡易发性预测。对比分析IV–SVM和IV–RF模型与目前研究中最常用的全区随机选择负样本的单独RF、SVM模型,以及从坡度小于2°的特定属性区内选择负样本的低坡度RF、SVM模型,为ML算法预测滑坡易发性中负样本的选择提供参考。
1 信息量–机器学习(IV–ML)模型理论 1.1 IV–ML建模流程本文所提出的IV–ML模型预测滑坡易发性的建模思想为利用不需要负样本的IV统计算法获得低易发区,并在该区随机选择ML易发性建模过程中需要的负样本数据,在确保负样本低易发性的同时,不对环境因子进行人为选择。建模过程如下:1)根据历史滑坡和环境因子数据之间的空间分布关系,利用IV模型计算各滑坡环境因子的信息量值;2)以环境因子总信息量值为基础,预测并绘制初步的滑坡易发性图,从极低和低易发区中随机选取“非滑坡”负样本数据;3)整合“历史滑坡”正样本和“非滑坡”负样本构成训练样本集,建立IV–RF、IV–SVM模型;4)对比IV–SVM、IV–RF模型与单独SVM、RF模型和低坡度SVM、RF模型的预测精度;5)深入讨论分析各模型的精度统计指标、ROC曲线和易发性指数分布。具体流程如图1所示。
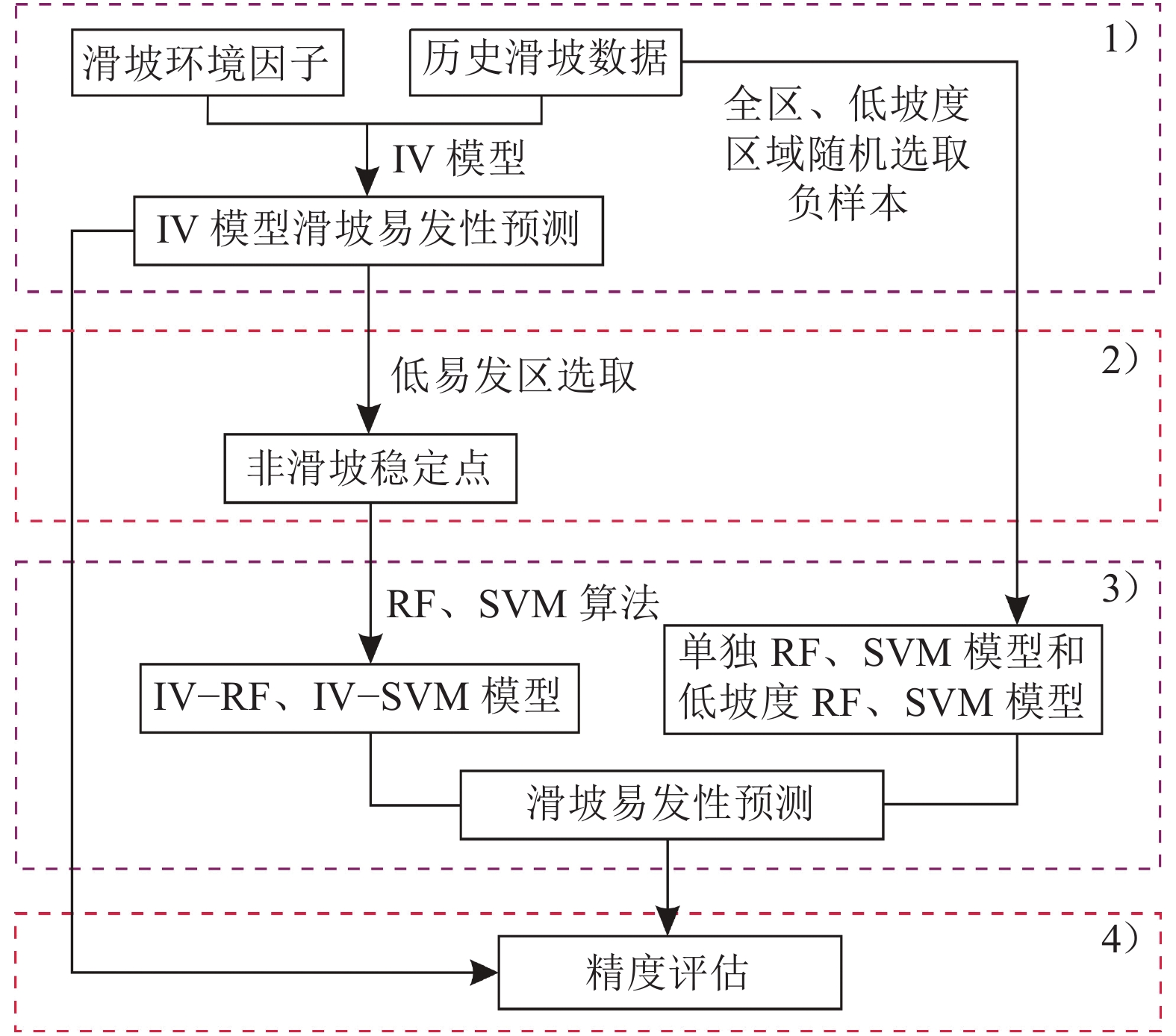 |
| 图1 IV–ML模型预测滑坡易发性流程图 Fig. 1 Flow chart of landslide susceptibility prediction by IV–ML model |
1.2 信息量(IV)模型及负样本选择
IV模型将统计分析的已发生滑坡点的环境因子属性值转化为反映滑坡易发性的可以量化的信息量值[15-16],单个影响因子在不同分级标准下的信息量表达式为:
| $ I\left( Y,{{X}_{i}} \right)=\ln \left(\frac{{S_{i}}/S}{{A}_{i}/{A}} \right) $ | (1) |
式中,Y为滑坡灾害事件,Si为在环境因子Xi在分级区间内的滑坡面积,S为全区滑坡总面积,
研究区各评价单元内所有环境因子的总信息量值的表达式为:
| $ I=\sum\limits_{i=1}^{n}{I\left( Y,{{X}_{i}} \right)}=\sum\limits_{i=1}^{n}{\ln \left(\frac{{S_{i}}/S}{{A}_{i}/{A}} \right)} $ | (2) |
式中,n为环境因子个数。
在ArcGIS10.2中,利用“Map Algebra”功能实现环境因子信息量图层叠加,即可得到全区内所有评价单元的总信息量值,并将其作为评判研究区滑坡易发性的依据;利用自然断点法将研究区分成极高、高、中等、低和极低5个级别易发区间;利用“Create Random Points”功能在低和极低易发区随机采样,以获得负样本数据。
1.3 机器学习模型 1.3.1 支持向量机(SVM)模型SVM模型通过在高维空间内构建超平面,利用该超平面对数据进行最远距离的分类,并在该空间内进行分离预测类别[18],如式(3)所示:
| $ f(x) = \omega \phi (x) + \theta $ | (3) |
式中,f(x)为SVM的回归函数,
| $ k\left( {{\boldsymbol{x}},{\boldsymbol{y}}} \right) = \exp \left( { - \frac{{{{\left\| {{\boldsymbol{x}} - {\boldsymbol{y}}} \right\|}^2}}}{{2{\alpha ^2}}}} \right) $ | (4) |
式中,x、y为输入向量,α为RBF核函数的宽度参数。
1.3.2 随机森林模型RF为由多棵决策树集合而成的一类有监督的强分类器,其最大的特点是随机森林生成过程中有两个随机过程:样本的随机有放回抽样和特征变量子空间的随机选择[19]。每棵决策树的节点分裂以基尼系数(Gini Index)作为杂质函数,如式(5)所示:
| $ {\text{Gini Index = 1 }}-\sum\limits_c {{p^2}\left( {c\left| t \right.} \right)} $ | (5) |
式中,c为分类类别个数,t为决策树的节点,p为c的相对频率。RF中决策树的生长过程是以随机抽取特定数量的特征变量进行节点分裂,抽取变量个数一般为总数的平方根。通过这种模型的构建思路,可使RF分类器利用个体分类树间差异性的增加,提升建模性能且避免模型过拟合。
1.4 滑坡易发性建模精度评价基于混淆矩阵计算的Kappa系数(Kappa coefficient,KC)和准确率(Overall Accuracy,OA)是评价滑坡易发性预测模型性能的重要指标,如式(6)和(7)所示:
| $ {\text{OA}} = \frac{{TP + TN}}{{TP + TN + FP + FN}} $ | (6) |
| $\begin{aligned}[b] {\text{KC}} =& \frac{{{\rm{OA}}{{ - }}{P_{\text{e}}}}}{{1 - {P_{\text{e}}}}},\\{P_{\text{e}}} =& \frac{{\left( {TP + FN} \right)\left( {TP + FP} \right) + \left( {TN + FN} \right)\left( {TN + FP} \right)}}{{{{\left( {TP + TN + FP + FN} \right)}^2}}} \end{aligned}$ | (7) |
式(6)和(7)中:TP和FP分别为被正确分类和被错误分类为滑坡样本个数;TN和FN分别为被正确分类和被错误分类的非滑坡样本个数[2];准确率OA为模型精度的综合评价指标;Kappa系数(KC)反映了易发性建模的可靠性,当Kappa系数大于0.6时,表明建模可靠性高,大于0.8时,表明建模过程非常完善。另外,基于混淆矩阵可以绘制ROC曲线,该曲线下面积(AUC)被广泛用于模型精度评估[20],AUC值越接近1,表明模型预测易发性的精度越高。
2 建模数据源 2.1 瑞金市概况瑞金地处江西东南部(115°41′10″N~116°21′49″E),面积约为2 435.8 km2,属中亚热带湿润气候,1968—2019年的年均降雨量达1 663.5 mm,降水多集中在3—6月。区内地势南北高、中部低,地形坡度小于30°的区域占全区的90%以上。区内地层出露比较齐全,除奥陶、志留系缺失外,其余时代地层均有出露;其中,变质岩类分布最广,其次为碎屑岩类和岩浆岩类,三者占全区面积的93.34%。研究区位于宁于坳陷和武夷隆起带,在地质发育期构造变形强烈,岩浆活动频繁,以强烈的断裂活动为特色,如图2所示。
 |
| 图2 研究区位置及地质构造 Fig. 2 Location and geological structure of the study area |
根据瑞金1∶50 000地灾调查资料,1970—2013年间,研究区共发生滑坡155处,造成的房屋损坏达100多间,受灾人口2 000多人。区域内滑坡主要以小型为主,经民宅基地、公路和水利工程设施建设等人工削坡后,自然的坡体松散堆积物(土质)或破碎岩体(主要为千板状板岩及存在顺坡层面或裂面的岩石)失去了支撑力和平衡,形成全新的边坡临空面,在强降雨作用下容易诱发边坡失稳。为实现滑坡范围的最优表达,将历史滑坡在Google Earth中识别并绘制成矢量多边形,如图3所示。
 |
| 图3 研究区Google Earth高清遥感影像滑坡俯视图 Fig. 3 Top view of high resolution remote sensing image of landslides from Google Earth in study area |
2.2 滑坡环境因子
滑坡发育受多种因素影响,主要包括地层岩性、地形特征、植被土壤等长时间形成的内在驱动因素,以及强降雨、工程活动、地震等在相对短时间内起作用的外部诱发因素。根据前人对山体滑坡环境因子的研究[7,21]、瑞金市滑坡发育与环境因子的关联性特征及滑坡野外考察情况,在尽可能收集到的环境因子数据的基础上,选取工程地质、地形特征、气象水文、地表覆被和土壤等几大类别环境因子作为滑坡易发性预测建模的输入变量,如表1和图4所示。
| 表1 滑坡环境因子 Tab. 1 Landslide environmental factors |
 |
 |
| 图4 滑坡环境因子及历史滑坡分布 Fig. 4 Landslide environmental factors and historical landslide distribution |
2.2.1 工程地质因子
境内出露有岩浆岩类、变质岩类、碎屑岩类、碳酸盐岩类及松散岩类等六大岩性类型,如图4(a)所示;不同岩性单元的边界如图4(b)所示。研究区断裂构造呈现相互穿插切割的形态,错综复杂;依据其空间发育方向可分为东西向、北东向、北北东、北西向及武夷山环状断裂等5组,如图4(c)所示。
2.2.2 地形与气象水文因子区内以低山丘陵为主,但南部的拔英乡及北部的瑞林、丁坡、下坝、大柏地等乡镇地势高差大,如图4(e)~
植被的根系有利于提高土体抗剪强度,对防止浅层堆积层滑坡有重要作用,用标准化植被指数(normalized difference vegetation index,NDVI)表示研究区植被发育程度,如图4(h)所示。瑞金交通以公路为主(图4(i)),公路建设依山傍水,尤其是公路的改建、扩建,会使公路两侧山体因人为的削坡而失稳[20]。土壤因子包括土壤类型、土壤砂粒和黏粒含量。土壤表层黏粒含量低,砂粒含量高,有利于水的渗透;底层黏粒含量高,砂粒含量低,易于形成滑动面。
3 瑞金市滑坡易发性预测 3.1 IV法选择负样本将整个研究区按30 m分辨率划分栅格单元,共计2 711 543个。利用GIS空间分析功能计算各栅格单元内所有环境因子的总信息量值,范围为–31~22。栅格单元的总信息量值越大,该栅格内滑坡发生的可能性就越大。图5为信息量法的滑坡易发性图及负样本点分布。如图5所示,负样本数量与正样本一致。将正样本栅格赋值为“1”,表示滑坡发生;负样本栅格赋值为“0”,表示滑坡不发生。选取70%的样本栅格数据作为研究区滑坡易发性预测模型的训练集,剩余的30%的样本栅格数据作为验证集评价预测模型精度(图1)。
 |
| 图5 信息量法的滑坡易发性图及负样本点分布 Fig. 5 Landslide susceptibility map by IV method and distribution of negative sample points |
同时,在滑坡一定缓冲区外的其他区域随机选择负样本,以便构建单独SVM和RF模型;并在低坡度区域(主要为坡度<2°的城市、河道和沟谷)随机选取负样本,构建低坡度SVM和RF模型。最后,对比分析这3类不同负样本选择方案的机器学习模型易发性建模性能。
3.2 IV–SVM模型与其他SVM模型滑坡易发性预测性能对比SVM模型的构建是在EnMAP–Box 2.1软件[23]中实现的,使用内部验证的2维网格搜索法获得IV–SVM模型的最优高斯核函数宽度参数α和正则化参数c分别为0.1和10。同样方法可得到单独SVM和低坡度SVM模型的建模参数分别为0.1、100和0.1、1 000。为方便不同模型间的对比研究,将所有模型预测的滑坡发生概率值分为极低(0~0.2)、低(0.2~0.4)、中等(0.4~0.6)、高(0.6~0.8)和极高(0.8~1.0)5个易发性级别。整体而言,各模型下的研究区滑坡易发性分级规律类似,但细节上存在较大差异,如图6所示。
 |
| 图6 基于SVM模型的滑坡易发性分区 Fig. 6 Landslide susceptibility generated based on SVM models |
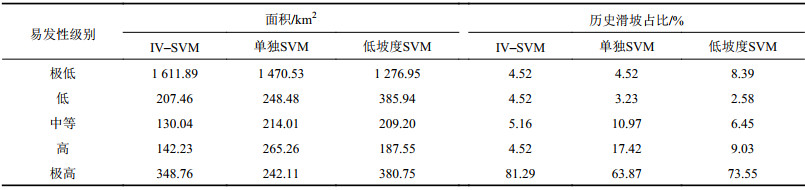
各类模型预测得到的滑坡易发区面积占比如表2所示。IV–SVM、单独SVM和低坡度SVM模型高和极高易发区面积之和分别为491.99、507.37和568.30 km2,其中,历史滑坡占比分别为85.61%、81.29%和82.58%,IV-SVM模型高和极高易发区历史滑坡占比最高。该结果间接反映了IV–SVM模型对滑坡易发性的预测性能更优。
| 表2 基于SVM模型的不同易发性等级区域面积及历史滑坡分布 Tab. 2 Areas of different susceptibility levels and distribution of historical landslides based on SVM models |
 |
3.3 IV–RF模型与其他RF模型滑坡易发性预测性能对比
RF模型的建立是采用与第3.2节中相同的环境因子数据集和训练集,在EnMAP–Box 2.1软件中实现的。RF模型建立过程中决策树的个数(NT)对模型精度有重要影响。当NT较小时,RF的预测性能较差;当NT越大时,RF的建模性能越好。但是,随着NT的增大,RF模型复杂程度也增大,建模耗费的时间也更长。多次实验表明,当决策树个数增加到300时,RF的预测性能达到稳定[24],并以此建立预测滑坡易发性的IV–RF、单独RF和低坡度RF模型。
滑坡易发性分区图的绘制标准也与第3.2节一致,如图7所示。
 |
| 图7 基于RF模型的滑坡易发性分区 Fig. 7 Landslide susceptibility generated based on RF models |
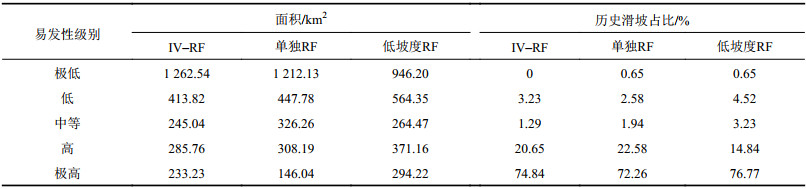
IV–RF、单独RF和低坡度RF模型中,高和极高易发区面积分别为518.99、454.23和665.38 km2,其中,历史滑坡占比分别为95.49%、94.84%和91.61%,IV–RF模型高和极高易发区历史滑坡占比最高,如表3所示。
| 表3 基于RF模型的不同易发性等级区域面积及历史滑坡分布 Tab. 3 Areas of different susceptibility levels and distribution of historical landslides based on RF models |
 |
3.4 模型精度评价 3.4.1 精度统计指标
各模型的Kappa系数和准确率等评价指标如表4所示。
| 表4 不同模型验证指标 Tab. 4 Validation indicators of different models |
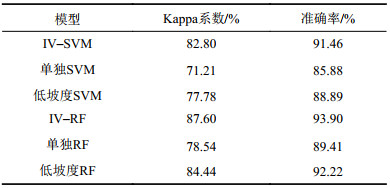 |
由表4可知:IV–SVM和IV–RF耦合模型验证集的准确率值分别为91.46%和93.90%,均高于传统采样预测模型;RF模型预测易发性的精度高于SVM,其中,IV–RF耦合模型的Kappa系数为87.60%,表示该模型具有非常强的可靠性。总之,耦合模型精度最高,低坡度模型次高,单独模型精度最低。
3.4.2 ROC曲线精度图8为各模型的ROC曲线。由图8可知:相比传统采样的单独SVM、RF模型和低坡度SVM、RF模型,IV–SVM和IV–RF耦合模型的ROC曲线的AUC值更高,进一步证明了基于IV模型负样本采样方法的优势;IV–RF模型ROC曲线的AUC值最高,为0.988,也说明RF算法的滑坡易发性预测性能好于SVM算法。
 |
| 图8 不同模型的ROC曲线 Fig. 8 ROC curves of the different models |
另外,单独SVM和RF模型ROC曲线的AUC值分别为0.838和0.943,而低坡度SVM和RF模型ROC曲线的AUC值分别为0.879和0.967。可见,在低坡度地区随机选取负样本的SVM和RF模型精度优于单独SVM和RF模型。低坡度的极端采样方法对SVM和RF建模非常有利,但人为提高了坡度因子的贡献度,过高估计了灾害的易发程度,这点从低坡度SVM和RF模型的极高易发区大于单独SVM、RF模型和IV–SVM、IV–RF模型的结论中也可以得到印证。
3.4.3 滑坡易发性指数分布规律将所有模型预测概率值分为100个区间,统计研究区不同概率区间的栅格数量,计算易发性指数分布的均值和标准差,结果如图9所示。均值表示滑坡易发性指数分布的平均水平,标准差表示易发性指数围绕均值的离散程度,二者可用来分析不同模型预测结果的不确定性。由图9可知:IV–SVM、单独SVM和低坡度SVM模型的易发性指数分布规律为低概率和高概率区间分布高,中间概率区间分布低;其中,IV–SVM模型的平均值小于单独SVM和低坡度SVM模型,而标准差大于低坡度SVM模型和单独SVM模型。IV–RF、低坡度RF和单独RF模型的易发性概率分布规律为随预测概率值的增加而逐渐减小;其中,IV–RF模型均值小于单独RF和低坡度RF模型,标准差大于单独RF模型而小于低坡度RF模型。此外,SVM模型的标准差均大于RF模型,这与其概率小于0.01区间的栅格数量极高相关。
 |
| 图9 不同模型的易发性指数分布 Fig. 9 Susceptibility indexes distribution of different models |
IV–SVM和IV–RF模型既具备单独SVM和单独RF模型随机采样的优点,又在综合所有因子信息量值的基础上兼顾滑坡的易发性。因此,整体上IV–SVM和IV–RF模型的易发性概率分布的平均值小而标准差大。结合精度统计指标和ROC曲线精度结果可知,基于IV模型负样本选择的SVM和RF耦合模型具有更高的精度和更低的不确定性。
4 讨 论 4.1 滑坡易发性空间分布整体而言,本文提出的多个基于IV–ML的滑坡易发性预测模型的结果类似。研究区滑坡极高易发区主要分布在第四纪残坡积层和其他层岩性的接触带及人类活动密集区域;高易发区主要扩展在极高易发区的周围,集中分布在东部的瑞林镇和岗面乡、中部的九堡镇和云石山镇及南部的谢坊镇;中等易发区明显出现在道路两侧和地层界线交界处;低和极低易发区分布在受人类活动影响较小的植被丰富地区。
4.2 滑坡易发性预测模型分析RF模型中单个决策树预测器独特的树状结构能够准确检测到特征因子间的相关关系,有效处理非线性数据。同时,RF模型的集成和随机特征使其具有受数据的干扰影响较小、判断准确率高和有效防止过拟合的滑坡易发性建模优势[8]。部分专门探讨机器学习模型预测滑坡易发性性能的文献[24-28]显示:RF表现出了比逻辑回归、SVM和常规人工神经网络等其他模型更高的预测精度,更适用于滑坡易发性制图。本文研究结果与这些文献结论一致。
4.3 IV模型负样本选择的合理性ML模型在环境因子拟合上的优点依赖于训练数据即“历史滑坡”正样本和“非滑坡”负样本,可见选择“非滑坡”样本点的这一因素对机器学习建模影响很大。单独SVM和RF模型的负样本是通过在研究区内随机均匀选择的方式来实现的,不存在人为选择干扰,对环境因子的影响程度较小。其优点主要体现在模型预测的低风险区域分布均匀,且极高和高风险区面积较小,整体精度也较好。目前的大部分研究均采用这种采样方法,但该方法的问题是所选择的非滑坡点不能保证其稳定性,可能为滑坡发生的潜在点。以往研究中对负样本的不确定性的关注太少,引起易发性预测结果误差较大。
低坡度SVM和RF模型的负样本分布在瑞金市的地形平坦地区,保证了所选择的非滑坡点的稳定性且预测精度也较好。但该模型最大的问题是过分强调坡度的作用,随机森林模型中因子重要性排序结果显示出坡度的重要性排在前列[12,24],导致该模型预测结果中的极高和高易发性区面积较大,且对高坡度的稳定区域的识别能力弱。
对于负样本选择这一问题,缪亚敏等[6]依据研究区地理环境的相似性规律,将与正样本的地理环境不相似的点作为负样本;黄发明等[29]提出自组织映射神经网络方法,并绘制初始滑坡易发性图,从极低易发区选择非滑坡样本。以上研究均通过合理地选择负样本提高了ML模型的精度。本文在上述分析中,选择计算方法更简单、预测精确的IV模型提取负样本,在考虑到每个因子影响程度,确保负样本选择客观准确的同时,降低了对环境因子影响。建模结果也显示,IV–ML模型预测出了规律更显著、精度更高的滑坡易发性结果。下一步研究可重点关注提高滑坡易发性建模效率的方法,探究负样本数量对建模结果的影响,以降低机器学习模型的不确定性及其干扰因素。
5 结 论为构建更为合理的滑坡易发性预测模型,针对ML建模中负样本的选择问题,构建了IV–SVM和IV–RF模型预测瑞金滑坡易发性;并与单独SVM、RF模型与低坡度SVM、RF模型做对比,开展建模讨论。
结果表明:IV–SVM和IV–RF模型具有比单独SVM、RF模型及低坡度SVM、RF模型更高的滑坡易发性预测精度且更有效地反映了滑坡易发性的空间分布规律。可见,基于IV法的滑坡负样本选择方案优于全区随机选择负样本及从坡度小于2°的特定属性区内随机选择负样本的方案,选择的负样本准确性更高且具有广泛的代表性。因此,利用IV法选择的负样本可作为ML模型预测滑坡易发性的基础。另外,RF算法相较于SVM模型具有更高的滑坡易发性预测精度。综上,IV–RF等类似耦合模型能够弥补单独模型存在的缺点,更加适合滑坡易发性预测建模。
| [1] |
Petley D. Global patterns of loss of life from landslides[J]. Geology, 2012, 40(10): 927-930. DOI:10.1130/G33217.1 |
| [2] |
Huang Yu,Zhao Lu. Review on landslide susceptibility mapping using support vector machines[J]. Catena, 2018, 165: 520-529. DOI:10.1016/j.catena.2018.03.003 |
| [3] |
Huang Faming,Ye Zhou,Yao Chi,et al. Uncertainties of landslide susceptibility prediction:Different attribute interval divisions of environmental factors and different data-based models[J]. Earth Science, 2020, 45(12): 4535-4549. [黄发明,叶舟,姚池,等. 滑坡易发性预测不确定性:环境因子不同属性区间划分和不同数据驱动模型的影响[J]. 地球科学, 2020, 45(12): 4535-4549.] |
| [4] |
Zhu Axing,Miao Yamin,Lin Yang,et al. Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping[J]. Catena, 2018, 171: 222-233. DOI:10.1016/j.catena.2018.07.012 |
| [5] |
Huang Faming,Cao Zhongshan,Jiang Shuihu,et al. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model[J]. Landslides, 2020, 17(12): 2919-2930. DOI:10.1007/s10346-020-01473-9 |
| [6] |
Miao Yamin,Zhu Axing,Yang Lin,et al. A method for quantifying the reliability of landslide pseudo-absence samples based on geographic environmental similarity[J]. Progress in Geography, 2016, 35(7): 860-869. [缪亚敏,朱阿兴,杨琳,等. 一种基于地理环境相似度的滑坡负样本可信度度量方法[J]. 地理科学进展, 2016, 35(7): 860-869. DOI:10.18306/dlkxjz.2016.07.007] |
| [7] |
Guo Zizheng,Yin Kunlong,Huang Faming,et al. Evaluation of landslide susceptibility based on landslide classification and weighted frequency ratio model[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(2): 287-300. [郭子正,殷坤龙,黄发明,等. 基于滑坡分类和加权频率比模型的滑坡易发性评价[J]. 岩石力学与工程学报, 2019, 38(2): 287-300.] |
| [8] |
Wu Runze,Hu Xudong,Mei Hongbo,et al. Spatial susceptibility assessment of landslides based on random forest:A case study from Hubei section in the Three Gorges Reservoir Area[J]. Earth Science, 2021, 46(1): 321-330. [吴润泽,胡旭东,梅红波,等. 基于随机森林的滑坡空间易发性评价:以三峡库区湖北段为例[J]. 地球科学, 2021, 46(1): 321-330.] |
| [9] |
Xu Shenghua,Liu Jiping,Wang Xianghong,et al. Landslide susceptibility assessment method incorporating index of entropy based on support vector machine:A case study of Shaanxi province[J]. Geomatics and Information Science of Wuhan University, 2020, 45(8): 1214-1222. [徐胜华,刘纪平,王想红,等. 熵指数融入支持向量机的滑坡灾害易发性评价方法——以陕西省为例[J]. 武汉大学学报(信息科学版), 2020, 45(8): 1214-1222.] |
| [10] |
Dou J,Yunus A P,Bui D T,et al. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island,Japan[J]. Science of the Total Environment, 2019, 662: 332-346. DOI:10.1016/j.scitotenv.2019.01.221 |
| [11] |
Kavzoglu T,Sahin E K,Colkesen I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis,support vector machines,and logistic regression[J]. Landslides, 2014, 11(3): 425-439. DOI:10.1007/s10346-013-0391-7 |
| [12] |
Choi J,Oh H J,Won J S,et al. Validation of an artificial neural network model for landslide susceptibility mapping[J]. Environmental Earth Sciences, 2011, 60(3): 473-483. |
| [13] |
Miao Yamin,Zhu Axing,Yang Lin,et al. A new method of pseudo absence data generation in landslide susceptibility mapping[J]. Geography and Geo-Information Science, 2016, 32(4): 61-67. [缪亚敏,朱阿兴,杨琳,等. 滑坡危险度制图中一种新型的负样本采样方法[J]. 地理与地理信息科学, 2016, 32(4): 61-67. DOI:10.3969/j.issn.1672-0504.2016.04.011] |
| [14] |
Xiao Chenchao,Tian Yuan,Shi Wenzhong,et al. A new method of pseudo absence data generation in landslide susceptibility mapping with a case study of Shenzhen[J]. Science China(Technological Sciences), 2010, 53(SupplI): 75-84. DOI:10.1007/s11431-010-3219-x |
| [15] |
Li Wenbin,Fan Xuanmei,Huang Faming,et al.Influence law of different environmental factor connection methods and data-based models on landslide susceptibility prediction modeling[J/OL].Earth Science1-20[2021–11–02].http://kns.cnki.net/kcms/detail/42.1874.P.20210506.1457.004.html. 李文彬,范宣梅,黄发明,等.不同环境因子联接方法和数据驱动模型对滑坡易发性预测建模的影响规律[J/OL].地球科学:1-20[2021-11-02].http://kns.cnki.net/kcms/detail/42.1874.P.20210506.1457.004.html. |
| [16] |
Wang Jiajia,Yin Kunlong,Xiao Lili,et al. Landslide susceptibility assessment based on GIS and weighted information value:A case study of Wanzhou district,Three Gorges Reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(4): 797-808. [王佳佳,殷坤龙,肖莉丽. 基于GIS和信息量的滑坡灾害易发性评价——以三峡库区万州区为例[J]. 岩石力学与工程学报, 2014, 33(4): 797-808.] |
| [17] |
Zhang Qikai,Ling Sixiang,Li Xiaoning,et al. Comparison of landslide susceptibility mapping rapid assessment models in Jiuzhaigou county,Sichuan province,China[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(8): 1595-1610. [张玘恺,凌斯祥,李晓宁,等. 九寨沟县滑坡灾害易发性快速评估模型对比研究[J]. 岩石力学与工程学报, 2020, 39(8): 1595-1610.] |
| [18] |
Cortes C,Cortes C,Vapnik V,et al. Support-vector networks[J]. Machine Learning, 1995, 20: 273-297. |
| [19] |
Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [20] |
Huang Faming,Cao Zhongshan,Guo Jianfei,et al. Comparisons of heuristic,general statistical and machine learning models for landslide susceptibility prediction and mapping[J]. Catena, 2020, 191: 104580. DOI:10.1016/j.catena.2020.104580 |
| [21] |
Liu Yuanbo,Niu Ruiqing,Yu Xianyu,et al. Application of the rotation forest model in landslide susceptibility assessment[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 959-964. [刘渊博,牛瑞卿,于宪煜,等. 旋转森林模型在滑坡易发性评价中的应用研究[J]. 武汉大学学报(信息科学版), 2018, 43(6): 959-964.] |
| [22] |
Liu Jian,Li Shulin,Chen Tao. Landslide susceptibility assesment based on optimized random forest model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1085-1091. [刘坚,李树林,陈涛. 基于优化随机森林模型的滑坡易发性评价[J]. 武汉大学学报(信息科学版), 2018, 43(7): 1085-1091.] |
| [23] |
Waske B,van der Linden S,Oldenburg C,et al. Image RF—A user-oriented implementation for remote sensing image analysis with random forests[J]. Environmental Modelling & Software, 2012, 35: 192-193. |
| [24] |
Zhou Xiaoting,Wu Weicheng,Lin Ziyu,et al. Zonation of landslide susceptibility in Ruijin,Jiangxi,China[J]. International Journal of Environmental Research and Public Health, 2021, 18(11): 5906. DOI:10.3390/ijerph18115906 |
| [25] |
Achour Y,Pourghasemi H R. How do machine learning techniques help in increasing accuracy of landslide susceptibility maps?[J]. Geoscience Frontiers, 2020, 11(3): 871-883. DOI:10.1016/j.gsf.2019.10.001 |
| [26] |
Merghadi A,Yunus A P,Dou J,et al. Machine learning methods for landslide susceptibility studies:A comparative overview of algorithm performance[J]. Earth-Science Reviews, 2020, 207: 103225. DOI:10.1016/j.earscirev.2020.103225 |
| [27] |
Shahri A A,Spross J,Johansson F,et al. Landslide susceptibility hazard map in southwest Sweden using artificial neural network[J]. Catena, 2019, 183: 104225. DOI:10.1016/j.catena.2019.104225 |
| [28] |
Huang Faming,Chen Jiawu,Tang Zhipeng,et al. Uncertainties of landslide susceptibility prediction under different spatial resolutions and different proportions of training and testing datasets[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1155-1169. [黄发明,陈佳武,唐志鹏,等. 不同空间分辨率和训练测试集比例下的滑坡易发性预测不确定性[J]. 岩石力学与工程学报, 2021, 40(6): 1155-1169.] |
| [29] |
Huang Faming,Yin Kunlong,Jiang Shuihua,et al. Landslide susceptibility assessment based on clustering analysis and support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 156-167. [黄发明,殷坤龙,蒋水华,等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 2018, 37(1): 156-167.] |
 2022, Vol. 54
2022, Vol. 54


