高效的无证书云数据审计方案

Contents Abstract Full text PDF

引用本文

杨海滨, 李瑞峰, 李秀广, 等. 高效的无证书云数据审计方案[J]. 工程科学与技术, 2022, 54(3): 72-79. DOI:10.15961/j.jsuese.202100953

YANG Haibin, LI Ruifeng, LI Xiuguang, et al. Efficient Certificateless Cloud Data Auditing Scheme[J]. Advanced Engineering Sciences, 2022, 54(3): 72-79. DOI:10.15961/j.jsuese.202100953

高效的无证书云数据审计方案

杨海滨^1,2, 李瑞峰¹, 李秀广^1,3, 袁文勇¹, 易铮阁¹, 杨晓元^1,2

1. 武警工程大学密码工程学院，陕西西安 710086;
2. 网络与信息安全武警部队重点实验室，陕西西安 710086;
3. 西安电子科技大学综合业务网国家重点实验室，陕西西安 710071

收稿日期: 2021-09-21; 网络出版时间: 2022-05-12 14:13:40

作者简介: 杨海滨（1982—），男，副教授，博士. 研究方向：信息安全. E-mail：54537959@qq.com

基金项目: 国家重点研发计划项目（2017YFB0802000）；国家自然科学基金项目（62172436）；武警工程大学基础前沿研究基金项目（WJY202014）

摘要: 针对现有无证书云审计方案中，使用了幂指数、双线性映射、点哈希映射等大开销运算，导致审计效率不高的问题，本文提出一种高效的无证书云数据完整性验证方案。方案在密钥生成阶段，使用无证书签名技术，由密钥生成中心（key generating center, KGC）与用户合作生成用户的公私钥，能够避免审计系统的安全对于KGC安全的强依赖性，既解决了公钥基础设施（public key infrastructure，PKI）体制下的云审计方案中公钥证书管理复杂的缺点，又能够解决基于身份的云审计方案所固有的密钥托管问题。在数据预处理阶段，用户将数据加密、分块，保护了数据内容隐私，且降低了方案的计算与通信开销。在数据动态更新阶段，方案使用虚拟索引数据结构实现云端数据块的动态更新（插入、删除、修改），能够避免标签重复计算导致的额外计算开销。在数据审计阶段，由第三方审计者（third party auditor，TPA）代替用户对来自云端的完整性证据进行验证，能够减轻用户的计算负担。本文在安全性分析部分，证明了方案能够抵抗来自云端的替代攻击，可实现隐私保护，且能够抵抗两类敌手的伪造攻击。在方案性能分析部分，先对本方案和现有方案进行数值分析与对比，再利用JPBC库进行实验，结果表明本方案的计算开销明显降低。

关键词: 云存储数据完整性数据持有证明无双线性对无证书签名

Efficient Certificateless Cloud Data Auditing Scheme

YANG Haibin^1,2, LI Ruifeng¹, LI Xiuguang^1,3, YUAN Wenyong¹, YI Zhengge¹, YANG Xiaoyuan^1,2

1. College of Cryptographic Eng., Eng. Univ. of People’s Armed Police, Xi’an 710086, China;
2. Key Lab. of the Armed Police Force for Network and Info. Security, Xi’an 710071, China;
3. State Key Lab. of Integrated Service Networks, Xidian Univ., Xi’an 710071, China

Abstract: In order to solve the problem of low audit efficiency due to the use of power exponent, bilinear mapping, point hash mapping and other expensive operations in the existing certificateless cloud auditing scheme, an efficient certificateless cloud auditing scheme was designed in this paper. In the key generation stage, combined with the certificateless signature technology, the user’s public and private keys were generated by the key generating center (KGC) in cooperation with the user, so that the strong dependence of auditing system security on KGC security was avoided. Consequently, the shortcomings of complex public key certificate management under the public key infrastructure (PKI) system and the inherent key escrow issues under the identity-based cloud audit scheme were solved. In the data preprocessing stage, the data was encrypted and divided into blocks. Therefore, the data content privacy was protected and the calculation and communication overhead of the scheme was reduced. In the data dynamic update stage, the virtual index data structure was used to realize the insertion, deletion and modification of data blocks. As a result, the extra computational overhead caused by label recalculation was avoided. In the data auditing stage, the task of users to verify the integrity evidence was replaced by a third party auditor (TPA), which reduces the user’s computational burden. In the section of security analysis, it was proved that the substitution attack from the cloud was resisted, the privacy protection was achieved, and the forgery attacks by two types of adversaries were resisted. In the performance analysis part, numerical analysis and comparison of the proposed scheme with the existing schemes were carried out on the JPBC library. The experiments show that the proposed scheme significantly reduces the computational cost.

Key words: cloud storage data integrity data possession proof no bilinear pair certificateless signature

云计算技术是近年来最受欢迎的分布式计算方式之一。作为一种以数据存储和管理为核心的云计算系统，云存储技术因其便利、经济、高扩展性等特点，已成为一种新兴的存储模式^[1]。然而，云存储技术在国内外飞速发展的同时，也暴露出许多安全隐患，尤其是用户云端数据的完整性可能遭受破坏^[2]。如何保证云端数据的完整性不被破坏，已成为当前研究的热点。

在早期的远程数据完整性验证方案中，审计者需要从云端下载所有数据，然后使用本地存储的元数据来验证完整性。这种方法需要的通信和计算成本较高，导致算力与存储空间的巨大浪费。2007年，Ateniese等^[3]首次正式定义数据持有性证明方案，该方案中，只需抽取部分数据内容进行审计，就能确认全部数据内容的完整性。2013年，Wang等^[4]首次将云审计与身份基密码体制^[5]结合，来审计云端数据的完整性，解决了审计方案中存在的证书管理复杂的问题。随后，研究者在基于身份的云审计方案中，添加数据动态更新、多用户批量审计、用户可撤销等各种功能，以满足用户的不同需求，由此基于身份的云审计方案研究成果趋向成熟。然而，基于身份的审计方案中仍存在密钥托管问题，即审计系统的安全性完全依赖于KGC的安全性及可信性，用户的私钥面临泄露的威胁。

针对基于身份的云审计方案中存在的密钥托管问题，2013年，Wang等^[6]首次提出无证书云审计方案，但He等^[7]指出，文献[6]方案在面对Ⅰ类型敌手时，攻击者可擅自替换用户的公钥，存在安全问题。Yang等^[8]提出一种群用户数据共享的无证书云审计方案，该方案支持对数据内容、用户身份隐私保护和数据动态更新，但该方案中，云端每验证一个标签，需计算3次双线性对，计算开销较大。Ming等^[9]提出的无证书云审计方案，实现了对于身份隐私的保护，但该方案中，即使所有外包数据都被云服务器删除，仍然能够伪造数据持有证明，并通过审计。Huang等^[10]的方案支持数据的批量审计功能，并且基于中国剩余定理实现了高效的密钥更新功能，但该方案中云端存储的是加密后的数据块和使用未加密数据块计算的标签，因此生成的证据并不能满足验证等式。Kang等^[11]将无证书云审计方案应用于无线体域网络，所提方案能抵抗恶意审计者，保护数据内容，但该方案中没有数据的动态更新过程。He等^[12]的方案能够保护用户隐私，但存在安全性漏洞^[13]，云服务器即使篡改了用户数据，也可以通过审计。Ji等^[14]对文献[12]进行安全性改进，重新定义了原文的安全模型，解决了其中的安全问题，但改进的方案中仍未描述云端数据的动态更新过程。Wu等^[15]对保护隐私的无证书云审计方案的安全模型进行定义，所提方案支持多用户群组身份隐私保护，但该方案未描述动态更新和数据内容隐私保护，且云端在生成证明时，需计算2倍挑战数据块数量的双线性对，计算负担较大。Zhang等^[16]设计的抵抗恶意审计者的无证书云审计方案没有数据动态更新的过程，且未实现数据隐私保护。He等^[17]将无证书审计方案应用于基于云的智能电网数据管理系统，降低了计算开销，但该方案中功能不够完善，未介绍动态更新或批量审计的过程。另外，上述大部分无证书方案在审计过程中使用了幂指数、点哈希函数、双线性配对等大开销运算，双线性配对在实际应用中实现较难且开销较大^[18]，降低了方案的审计效率。

针对上述问题，本文基于椭圆曲线密码和无证书签名技术，设计了无双线性对的高效无证书公共云审计方案；使用虚拟索引数据结构，实现了方案对云端数据的动态更新；使用对称加密算法保护了云数据的内容隐私；基于分叉引理和离散对数问题的困难性，证明了方案是安全可靠的。方案在解决了身份基密钥托管问题的基础上，审计效率更高，计算开销有明显降低。

1 系统模型与相关技术 1.1 系统模型

2013年，Wang等^[19]首次定义云审计方案中的系统模型，规范了审计方案中的挑战–响应数据验证流程。本方案中使用的无证书云审计系统模型在文献[19]的基础上，增加了实体KGC，如图1所示。

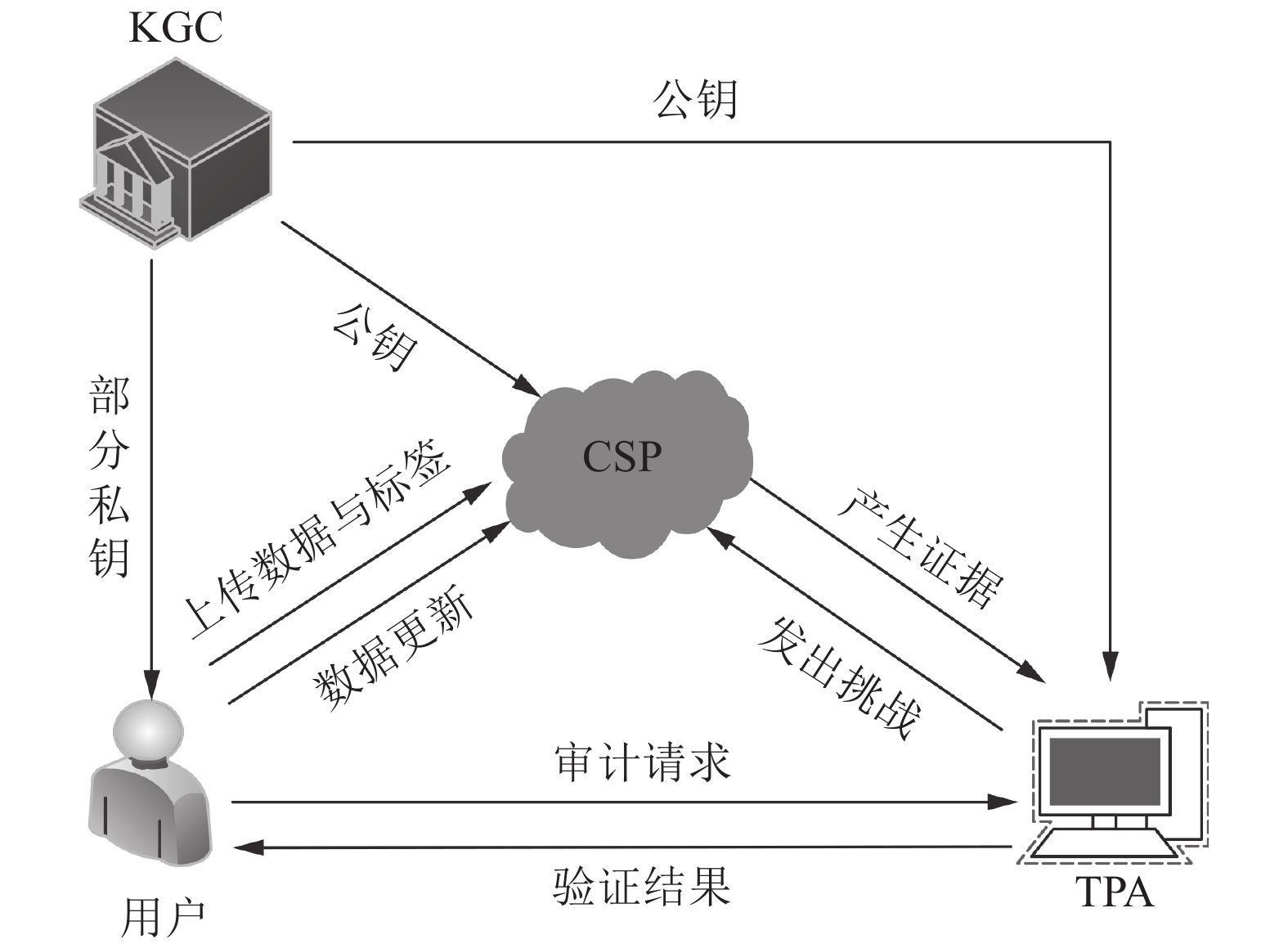图1 系统模型 Fig. 1 System model

图1中，用户是使用云存储服务的实体，也是审计工作的发起人。云服务提供商（cloud service provider，CSP）对外提供数据云端存储与管理服务。TPA是由用户委托的审计任务的执行者，能够节省用户的开销。KGC是密钥生成中心，为审计系统产生密钥。

审计流程如下：首先，KGC与用户合作生成用户的公私钥。然后，用户将要存储的数据文件使用对称加密算法盲化，将数据文件分块，对每一个数据块计算标签，发送数据块和标签至云端，并删除本地数据和标签。上传数据后，用户可更新云端数据。TPA在收到用户的审计请求时，发送挑战给云端。最后，云端使用接收到的挑战与自身存储的数据块和标签，生成数据持有证明发送给TPA，由TPA对证明进行验证，并将结果告知用户。

1.2 无证书签名

研究者们所提出的基于身份的密码体制虽然解决了复杂的证书管理问题，但导致了密钥托管问题的出现，即KGC的安全性和可靠性是决定系统安全性最为关键的因素，如果KGC存在漏洞，就会使用户私钥的安全性遭到威胁，随时可能被泄露^[20]。为此，后续Al–Riyami等^[21]提出了由用户和KGC一起生成用户私钥，并进行管理的无证书密码体制，可以很好地解决此类问题。

1.3 椭圆曲线密码

椭圆曲线密码（elliptic curve cryptogr-aphy，ECC）的概念由Miller^[22]和Koblitz^[23]提出，其定义如下：

设定大素数p、素数域 $ {F}_{p} $ 。 $ {F}_{p} $ 上的椭圆曲线满足方程 $ {y}^{2}={x}^{3}+ax+b $ ，其中 $ a,b\in {F}_{p} $ ，且要求 $4{a}^{3}+27{b}^{2}{{\rm{mod}}}\;q\ne $ $ 0$ 。无穷远点和椭圆曲线上的点构成一个加法循环群G。设P、Q为椭圆曲线上两点，k为整数，且满足 $ Q=k \cdot P $ ， $ k \cdot P $ 就是椭圆曲线上的倍点运算，已知P、Q求k的问题为椭圆曲线离散对数问题（elliptic curve discrete logarithm problem，ECDLP）。

2 高效的无证书云数据审计方案

本文使用胡冰洁等^[24]提出的数字签名算法构造无证书云审计方案，将其中对单个消息的签名和验证扩展到对多数据块的标签生成和完整性审计。本方案具体包括如下7个算法：

1） $ \text{Setup}\to ({p}_{p},{k}_{\text{ms}}) $ 。KGC生成公开参数 $ {p}_{p} $ 和主密钥 $ {k}_{\text{ms}} $ ，选择椭圆曲线上循环群 $ G $ ，定义大素数 $ q $ ，选择 $ G $ 中阶为 $ q $ 的生成元P，定义 $ {H}_{\mathrm{1,2},3}:\{\mathrm{0,1}{\}}^{*}\to {Z}_{q}^{*} $ ，选取随机数 $ {k}_{\text{ms}}\in {Z}_{q}^{*} $ 为系统主密钥，计算 $ {P}_{\text{pub}}={k}_{\text{ms}}\cdot P\in G $ 为系统主公钥，选取一个对称加密算法 $ E $ 作为数据盲化算法，选取合适的 $\; \rho =2^\delta $ （ $ \delta \in N^{*} $ ）作为虚拟索引的步长，真实索引相邻的两个数据块中间最多可以插入 $2^{\delta} -1$ 个数据块。另外，选择伪随机置换函数 $ \text{per}:\{\mathrm{0,1}{\}}^{s}\to $ $ \{\mathrm{0,1}{\}}^{n} $ （ $ s\ll n $ ）， $ \text{per} $ 以随机数字作为输入，并生成数量较多的伪随机数字流。秘密保存主密钥 $ {k}_{\text{ms}} $ ，公开参数 ${p}_{p}=\{q,P,{P}_{\text{pub}},{H}_{1},{H}_{2},{H}_{3},E,\rho \}$ 。

2） $ \text{KeyGen}({k}_{\text{ms}},{p}_{p})\to ({k}_{\text{us}},{k}_{\text{up}}) $ 。用户选择随机数 $ x\in {Z}_{q}^{*} $ ，计算 $ X=x\cdot P\in G $ ，将身份信息ID和X发送给KGC，KGC随机选取 $ r\in {Z}_{q}^{*} $ ，计算 $ {h}_{i}^{1}={H}_{1}({ID},R,X) $ ， $ R= $ $ r\cdot P\in G $ ， $ d=r+{k}_{\text{ms}}{h}_{i}^{1} $ ，将R和 $ d $ 发送给用户。用户私钥为 $ {k}_{\text{us}}=(x,d) $ ，公钥为 $ {k}_{\text{up}}=(X,R) $ 。

3） $\text{TagGen}(\text{file,}{k}_{\text{us}},{k}_{\text{up}},m)\to S_i$ 。用户将要存储的数据文件 $ \text{file} $ 进行对称加密盲化，得到 $ F=E\left(\text{file}\right) $ ，而后分为 $ n $ 个数据块，表示为 $ F=\{{m}_{1},{m}_{2},\cdots ,{m}_{n}\} $ 。对于每个数据块 $ {m}_{i}$ （ $ 1\le i\le n $ ），用户选取随机数 $ {k}_{i}\in {Z}_{q}^{*} $ ，计算 $ {K}_{i}= $ $ {k}_{i}\cdot P $ ，然后计算：

$ {h}_{i}^{2}={H}_{2}\left({m}_{i},{ID},{K}_{i},X,{\eta }_{i}\right) $

(1)

$ {h}_{i}^{3}={H}_{3}\left({m}_{i},{ID},{K}_{i},R,{\eta }_{i}\right) $

(2)

$ {S}_{i}={h}_{i}^{3}x+d+{k}_{i}{h}_{i}^{2} $

(3)

式中： $ {\eta }_{i}=i\cdot \rho \in {N}^{*} $ ， $ {\eta }_{i} $ 为数据块虚拟索引； $ {S}_{i} $ 为数据块的标签。最后用户发送 $ {K}_{i(1\le i\le n)} $ 至TPA，发送 $ \{{m}_{i},{K}_{i},{S}_{i}{\}}_{(1\le i\le n)} $ 至云端，并删除本地数据和标签。

4） $ \text{ChallengeGen}\to (c,{k}_{\text{per}}) $ 。TPA在收到用户的审计请求时，选取随机数 $ c\in {Z}_{q}^{*} $ 为审计数据块的数量，选取随机数 $ {k}_{\text{per}}\in {Z}_{q}^{*} $ 为函数 $ \text{per} $ 的密钥，发送 $ (c,{k}_{\text{per}}) $ 给云端。 $ \text{TPA}\mathrm{、}\text{CSP} $ 利用函数 $ \text{per} $ ，输入 $ {k}_{\text{per}} $ 产生被抽取的数据块索引 $ {i}_{j} $ 。

5） $ \text{ProofGen}(F,{S}_{i},c,{k}_{\text{per}})\to \text{proof} $ 。云端接收到挑战 $ (c,{k}_{\text{per}}) $ 后，计算获得被抽取的数据块索引 $ {i}_{j} $ 。计算聚合标签 $S={\displaystyle\sum _{j=1}^{c}}{S}_{{i}_{j}}$ ，将 $ \{S,{{m}_{{i}_{j}}}_{(1\le j\le c)}\} $ 作为 $ \text{proof} $ 发送给TPA。

6） $\text{VerifyProof}\left(\text{proof}\right)\to \text{Yes}\;\text{or}\;\text{No}$ 。TPA接收到来自CSP的 $ \text{proof} $ 后，对于每个数据块 $ {m}_{j} $ ，计算式（1）、（2）得到 $ h^2_j $ 、 $ h^3_j $ ，将其与proof用于验证式（4）是否成立：

$ \begin{aligned}[b]& \left({\sum\limits _{j=1}^{c}{h}_{j}^{2}}\right)^{-1}\left(S-{\sum\limits _{j=1}^{c}{h}_{j}^{3}}\cdot X-c\cdot R-\text{}c{H}_{1}\left({ID},R,X\right)\cdot {P}_{\text{pub}}\right)=\\&\qquad \qquad \qquad\qquad \qquad{\sum\limits _{j=1}^{c}}{K}_{j}\\[-20pt] \end{aligned} $

(4)

使用式（5）的推导过程证明，若式（4）成立，则云端数据是安全完整的：

$\begin{aligned}[b]& \left({\sum\limits _{j=1}^{c}{h}_{j}^{2}}\right)^{-1}\left({\sum\limits _{j=1}^{c}}(S_{j}\cdot P-{h}_{j}^{3}X)-c\cdot R-c{h}_{i}^{1}\cdot {P}_{\text{pub}}\right)= \left({\sum\limits _{j=1}^{c}}{h}_{j}^{2}\right)^{-1}\cdot \\& \Bigg({\sum\limits _{j=1}^{c}}({h}_{j}^{3}\cdot X+{h}_{j}^{2}\cdot {K}_{j})+cd\cdot P-{\sum\limits _{j=1}^{c}}{h}_{j}^{3}\cdot X-c\cdot R-c{h}_{i}^{1}\cdot {P}_{\text{pub}}\Bigg)=\\& \left({\sum\limits _{j=1}^{c}}{h}_{j}^{2}\right)^{-1}\cdot \Bigg({\sum\limits _{j=1}^{c}}{h}_{j}^{2}\cdot {K}_{j}+c(r+{k}_{\text{ms}}{h}_{i}^{1})\cdot P- c\cdot R-c{h}_{i}^{1}\cdot {P}_{\text{pub}}\Bigg)=\\&\;\; \left({\sum\limits _{j=1}^{c}}{h}_{j}^{2}\cdot {K}_{j}+c{k}_{\text{ms}}{H}_{1}\left({ID},R,X\right)\cdot P- c{H}_{1}\left({ID},R,X\right)\cdot {P}_{\text{pub}}\right)\cdot \\&\;\;\;\;\;\;\left({\sum\limits _{j=1}^{c}}{h}_{j}^{2}\right)^{-1}=\left({\sum _{j=1}^{c}}{h}_{j}^{2}\right)^{-1}{\sum_{j=1}^{c} }{h}_{j}^{2}\cdot {K}_{j}={\sum _{j=1}^{c}}{K}_{j}\\[-18pt] \end{aligned} $

(5)

7） $\text{DynamicUpdate}\left(F\right)\to {F}{{'}}$ 。本方案使用文献[25]的虚拟索引结构，从而更高效地实现对数据块的动态更新操作。审计方案中的所有实体需要维护一份数据块与虚拟索引对应的转换表。

在数据块 $ {m}_{i} $ 之后插入盲化加密后的新数据块 $ {m}_{i}' $ 时，用户计算 $ {m}_{i}' $ 的虚拟索引 $ {\eta }_{i}'=\left({\eta }_{i}+{\eta }_{i+1}\right)/2 $ ，然后利用式（1）、（2）、（3）计算 $ {m}_{i}' $ 的标签 $ {S}_{i}' $ 。用户发送插入请求和 $ {\eta }_{i}' $ 、 $ {m}_{i}' $ 、 $ {S}_{i}' $ 给云端，更新虚拟索引表。云端接收后，根据虚拟索引 $ {\eta }_{i}' $ 找到对应位置，插入 $ {m}_{i}' $ 与 $ {S}_{i}' $ ，并更新虚拟索引表。

删除数据块 $ {m}_{i} $ 时，用户发送删除请求和虚拟索引 $ {\eta }_{i} $ 给云端，更新虚拟索引表。云端接收后根据 $ {\eta }_{i} $ 查找对应位置，然后删除数据块 $ {m}_{i} $ 与相应标签 $ {S}_{i} $ ，并更新虚拟索引表。

修改数据块 $ {m}_{i} $ 为 $ {m}_{i}' $ 时，用户发送修改请求与虚拟索引 $ {\eta }_{i} $ 给云端，云端返回对应的数据块 $ {m}_{i} $ 。用户将 $ {m}_{i} $ 根据需要修改成 $ {m}_{i}' $ ，然后利用式（1）～（3）计算 $ {m}_{i}' $ 的标签 $ {S}_{i}' $ 。用户发送修改请求和 $ {\eta }_{i} $ 、 $ {m}_{i}' $ 、 $ {S}_{i}' $ 给云端。云端接收后，根据虚拟索引 $ {\eta }_{i} $ 找到对应位置，修改数据块和标签为 $ {m}_{i}' $ 与 $ {S}_{i}' $ 。

3 安全性证明 3.1 抗替代攻击

假设加密后的数据文件F中块 $ {m}_{i} $ 被删除，但 $ {m}_{i1} $ 、 $ {m}_{i2} $ 被完整保存，且在整个审计阶段，TPA和用户正确执行本方案。用户在 $ \text{TagGen} $ 阶段利用式（3）计算标签， $ {m}_{i1} $ 、 $ {m}_{i2} $ 的标签分别为：

$ {S}_{i1}={h}_{i1}^{3}x+d+{k}_{i1}{h}_{i1}^{2} $

(6)

$ {S}_{i2}={h}_{i2}^{3}x+d+{k}_{i2}{h}_{i2}^{2} $

(7)

设 $ {a}_{1},{a}_{2}\in {Z}_{q}^{*} $ ， $ {m}_{i} $ 对应的标签可以表示为：

$ \begin{aligned}[b] {S}_{i}=&{a}_{1}{S}_{i1}+{a}_{2}{S}_{i2}= {a}_{1}({h}_{i1}^{3}x+d+{k}_{i1}{h}_{i1}^{2})+\\&{a}_{2}({h}_{i2}^{3}x+d+{k}_{i2}{h}_{i2}^{2})=({a}_{1}{h}_{i1}^{3}+{a}_{2}{h}_{i2}^{3})x+\\&({a}_{1}+{a}_{2})d+{a}_{1}{h}_{i1}^{2}{k}_{i1}+{a}_{2}{h}_{i2}^{2}{k}_{i2} \end{aligned} $

(8)

将式（8）结果与 $ {h}_{i}^{3}x+d+{k}_{i}{h}_{i}^{2} $ 比较， $ m_{i1} $ 、 $ m_{i2} $ 代入式（9）：

$\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {a}_{1}{H}_{3}\left({m}_{i1}\right)+{a}_{2}{H}_{3}\left({m}_{i2}\right)={H}_{3}\left({m}_{i}\right),\\{a}_{1}{H}_{2}\left({m}_{i1}\right){k}_{i1}+{a}_{2}{H}_{2}\left({m}_{i2}\right){k}_{i2}={H}_{2}\left({m}_{i}\right) \end{array}\right.$

(9)

此时，式（9）成立的概率忽略不计，因此，在 $ {m}_{i} $ 被删除的情况下， $ m_{i1} $ 、 $ m_{i2} $ 不能替代 $ {m}_{i} $ 通过审计，本方案可以抵抗替代攻击。

3.2 不可伪造性 3.2.1 敌手 $ {\mathit{A}}_{1} $ 的不可伪造性

在随机谕言模型中，假设敌手 $ {A}_{1} $ 在多项式时间内，能够以不可忽略的概率 $ \varepsilon $ 伪造正确标签并通过审计，则存在一个多项式时间算法以 $[1/e({q}_{1}+{q}_{2}+1\left)\right]\cdot $ $ (1-1/e)\cdot (1/{q}_{{H}_{1}})\cdot \varepsilon$ 的概率成功解决ECDLP。在挑战过程中， $ {A}_{1} $ 执行 $ {q}_{1} $ 次部分私钥询问，执行 $ {q}_{2} $ 次完整私钥询问，执行 $ {q}_{{H}_{1}} $ 次 $ {H}_{1} $ 询问。

证明：设 $ a $ 是系统主密钥，算法 $ C $ 以 $ \left(P,aP\right) $ 为输入，求 $ a $ 的具体值。

$ C $ 运行 $ \text{Setup} $ 算法，输出 $ {P}_{p} $ ，发送给 $ {A}_{1} $ ，建立列表 $ {L}_{c} $ 、 $ {L}_{{H}_{1}} $ 和 $ {L}_{I} $ 。设定主密钥 $ {k}_{\text{ms}}=a\in {Z}_{q}^{*} $ ，计算 $ {P}_{\text{pub}}=a\cdot P\in G $ ， $ {L}_{{H}_{1}} $ 中元组格式为 $ \left({I}{{D}}_{i},{R}_{i},{h}_{i}^{1},{X}_{i}\right) $ ， $ {L}_{c} $ 中元组格式为 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ， $ {L}_{I} $ 存储着 $ {A}_{1} $ 的身份。在游戏之前， $ C $ 对于 $ {A}_{1} $ 的身份未知，需随机选择一个 $ {A}_{1} $ 的挑战身份 $ {I}{{D}}_{A} $ 。在游戏过程中， $ {A}_{1} $ 将使用 $ {q}_{1}+{q}_{2}+1 $ 个不同的挑战身份。游戏结束后， $ C $ 利用 $ {A}_{1} $ 解决ECDLP， $ C $ 猜中 $ {A}_{1} $ 身份的概率为 $ 1/({q}_{1}+{q}_{2}+1) $ 。游戏过程中， $ {A}_{1} $ 可执行的各种询问的定义如下：

①公钥询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户的公钥进行询问时， $ C $ 检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，则发送 $ {k}_{\text{u}{\text{p}}_{i}}=\left({X}_{i},{R}_{i}\right) $ 给 $ {A}_{1} $ ；否则，选择随机数 $ {x}_{i} $ 、 $ {h}_{i}^{1} $ 、 $ {d}_{i}\in {Z}_{q}^{*} $ ，计算 $ {X}_{i}={x}_{i}\cdot P $ ， $ {R}_{i}={d}_{i}\cdot P-{P}_{\text{pub}}\cdot {h}_{i}^{1} $ ，将 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ 、 $ \left({I}{{D}}_{i},{R}_{i},{h}_{i}^{1},{X}_{i}\right) $ 加入到 $ {L}_{c} $ 和 $ {L}_{{H}_{1}} $ 中，向 $ {A}_{1} $ 发送 $ {k}_{\text{u}{\text{p}}_{i}}=\left({X}_{i},{R}_{i}\right) $ 。

② $ {H}_{1} $ 询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行 ${H}_{1}({I}{{D}}_{i}, $ $ {R}_{i},{X}_{i})$ 询问时， $ C $ 检索 $ {L}_{{H}_{1}} $ ，若 $ {L}_{{H}_{1}} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{h}_{i}^{1},{X}_{i}\right) $ ，发送 $ {h}_{i}^{1} $ 给 $ {A}_{1} $ ；否则，执行公钥生成算法，生成元组 $ \left({I}{{D}}_{i},{R}_{i},{h}_{i}^{1},{X}_{i}\right) $ 并加入到 $ {L}_{{H}_{1}} $ 中，向 $ {A}_{1} $ 发送 $ {h}_{i}^{1} $ 。

③秘密值询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行秘密值询问时， $ C $ 检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，发送 $ {x}_{i} $ 给 $ {A}_{1} $ ；否则，执行公钥生成算法，向 $ {A}_{1} $ 发送 $ {x}_{i} $ 。

④部分私钥询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行部分私钥询问时，若 $ {I}{{D}}_{i}={I}{{D}}_{A} $ ， $ C $ 终止；若 $ {I}{{D}}_{i}\ne {I}{{D}}_{A} $ ，则 $ C $ 检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，发送 $ {d}_{i} $ 给 $ {A}_{1} $ ，否则，执行公钥生成算法，向 $ {A}_{1} $ 发送 $ {d}_{i} $ 。

⑤公钥替换询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行公钥替换询问 $ {k}_{\text{u}{\text{p}}_{i}}'=\left({R}_{i}',{X}_{i}'\right) $ 时， $ C $ 检索 $ {L}_{c} $ ，找到 $({I}{{D}}_{i},{R}_{i},{d}_{i}, $ $ {x}_{i},{X}_{i})$ ，将 $ {X}_{i} $ 、 $ {R}_{I{D}_{i}} $ 替换为 $ {X}' $ 、 $ {R}' $ 。

⑥完整私钥询问。当 $ {A}_{1} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行完整私钥询问时，若 $ {I}{{D}}_{i}={I}{{D}}_{A} $ ， $ C $ 终止；若 $ {I}{{D}}_{i}\ne {I}{{D}}_{A} $ ， $ C $ 检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，发送 $ {d}_{i} $ 、 $ {x}_{i} $ 给 $ {A}_{1} $ ，否则，执行公钥生成算法，向 $ {A}_{1} $ 发送 $ {d}_{i} $ 、 $ {x}_{i} $ 。

⑦标签生成询问。当 $ {A}_{1} $ 对身份 $ {I}{{D}}_{i} $ 、数据块 $ {m}_{i} $ 、公钥 $ {k}_{\text{u}{\text{p}}_{i}} $ 进行标签生成询问时， $ C $ 计算 $ {h}_{i}^{2} $ 、 $ {h}_{i}^{3} $ 和 $ {S}_{i} $ ，获得标签 $ {\sigma }_{i}=\left({K}_{i},{S}_{i}\right) $ ，然后将 $ {m}_{i} $ 和 $ {\sigma }_{i}=\left({K}_{i},{S}_{i}\right) $ 发送给 $ {A}_{1} $ ，并在列表 $ {L}_{I} $ 中记录身份消息 $ {I}{{D}}_{i} $ 。

伪造： $ {A}_{1} $ 输出一个关于数据块 $ {m}^{*} $ 、身份 $ {I}{{D}}^{*} $ 、公钥 $ {k}_{\text{up}}^{*} $ 的伪造签名 $ {\sigma }^{*} $ ，若 $ {I}{{D}}^{*}\ne {I}{{D}}_{A} $ ，则 $ C $ 终止；若 ${I}{{D}}^{*}={I}{{D}}_{A}$ ，且 $ {L}_{I} $ 中不存在 $ {I}{{D}}^{*} $ ，则生成一个有效伪造标签 $ {\sigma }^{*}= $ $ \left({K}^{*},{S}^{*}\right) $ 。由分叉引理^[26]可知，选择不同的哈希函数 $ {H}_{1} $ 与 $ {H}_{1}' $ ，能够得到额外的有效伪造标签 $ {\sigma }'={\left(K,S\right)}' $ ，则以下方程组成立：

$\qquad \qquad \left\{ \begin{array}{l}S={x}_{A}{h}_{A}^{3}+{r}_{A}+{k}_{\text{ms}}{h}_{A}^{1}+{k}_{A}{h}_{A}^{2},\\ {S}{{'}}={x}_{A}{h}_{A}^{3}+{r}_{A}+{k}_{\text{ms}} {{h}_{A}^{1}}'+{k}_{A} {h}_{A}^{2}\end{array}\right. $

(10)

根据式（10）计算得到 ${k}_{\text{ms}}=\dfrac{S-{S}{{'}}}{{h}_{A}^{1}-{{h}_{A}^{1}}'}$ ， $ C $ 利用 $ {A}_{1} $ 能够成功解决ECDLP。

定义事件 $ {E}_{1} $ 表示 $ {A}_{1} $ 在询问过程中不终止，事件 $ {E}_{2} $ 表示 $ {A}_{1} $ 在伪造过程中不终止，事件 $ {E}_{3} $ 表示 $ {A}_{1} $ 成功输出两个有效标签。则 $ P\left({E}_{1}\right) $ 和 $ P\left({E}_{2}\right) $ 分别为：

$ {\;\;\;\;\;\;\;\;\;\;\;\; P\left({E}_{1}\right)\ge \left(1-\frac{1}{{q}_{1}+{q}_{2}+1}\right)^{{q}_{1}+{q}_{2}}} $

(11)

$ P\left({E}_{2}\right)=\frac{1}{{q}_{1}+{q}_{2}+1} $

(12)

设 $ {A}_{1} $ 输出一个有效数据标签的概率为 $\varepsilon$ ，则 $ P\left({E}_{3}\right) $ 为：

$ {\;\;\;\;\;\;\;\;\;\;P\left({E}_{3}\right)\ge \frac{1}{e}\frac{1}{{q}_{1}+{q}_{2}+1}\left(1-\frac{1}{e}\right)\frac{1}{{q}_{{H}_{1}}}\varepsilon} $

(13)

若 $\varepsilon$ 不可忽略，则 $ C $ 能够以大于 $[1/e({q}_{1}+{q}_{2}+1)]\cdot $ $ (1-1/e)\cdot (1/{q}_{{H}_{1}})\cdot \varepsilon$ 的概率解决ECDLP。

3.2.2 敌手 $ {\mathit{A}}_{2} $ 的不可伪造性

在随机谕言模型中，假设敌手 $ {A}_{2} $ 在多项式时间内，能够以不可忽略的概率 $ \varepsilon $ 伪造正确标签并通过审计，则存在一个多项式时间算法以 $[1/e({q}_{2}+{q}_{3}+1)]\cdot $ $ (1-1/e)\cdot (1/{q}_{{H}_{3}})\cdot \varepsilon$ 优势成功解决ECDLP。在挑战过程中， $ {A}_{2} $ 执行 $ {q}_{2} $ 次部分私钥询问，执行 $ {q}_{2} $ 次完整密钥询问，执行 $ {q}_{{H}_{3}} $ 次 $ {H}_{3} $ 询问。

证明：设 $ a $ 是系统主密钥，算法 $ C $ 以 $ \left(P,aP\right) $ 为输入，求 $ a $ 的具体值。

$ C $ 运行 $ \text{Setup} $ 算法，输出 $ {P}_{p} $ 和 $ {k}_{\text{ms}} $ ，发送给 $ {A}_{2} $ ，建立列表 $ {L}_{c} $ 、 $ {L}_{{H}_{3}} $ 和 $ {L}_{I} $ 。 $ {L}_{{H}_{3}} $ 中元组格式为 $ \left({I}{{D}}_{i},{R}_{i},{h}_{i}^{3},{K}_{i}\right) $ ， $ {L}_{c} $ 中元组格式为 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ， $ {L}_{I} $ 存储着 $ {A}_{2} $ 的身份。在游戏之前， $ C $ 对于 $ {A}_{2} $ 的身份未知，需随机选择一个 $ {A}_{2} $ 的挑战身份 $ {I}{{D}}_{A} $ 。在游戏过程中， $ {A}_{2} $ 将使用 $ {q}_{2}+{q}_{3}+1 $ 个不同的挑战身份。游戏结束后， $ C $ 利用 $ {A}_{2} $ 解决ECDLP， $ C $ 猜中 $ {A}_{2} $ 身份的概率为 $ 1/({q}_{2}+{q}_{3}+1) $ 。游戏过程中， $ {A}_{2} $ 可执行的各种询问的定义如下：

①公钥询问。当 $ {A}_{2} $ 对身份为 $ {I}{{D}}_{i} $ 的用户的公钥进行询问时， $ C $ 检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，则发送 $ {k}_{\text{u}{\text{p}}_{i}}=\left({X}_{i},{R}_{i}\right) $ 给 $ {A}_{2} $ ；否则，若 $ {I}{{D}}_{i}\ne {I}{{D}}_{A} $ ，选择随机数 $ {x}_{i},{r}_{i}\in {Z}_{q}^{*} $ ，计算 $ {R}_{i}={r}_{i}\cdot P $ ， $ {X}_{i}={x}_{i}\cdot P $ 和 ${d}_{i}={r}_{i}+{k}_{\rm {ms}}{H}_{1} \left({I}{{D}}_{i}, $ $ {R}_{i},{X}_{i}\right)$ ，将 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ 加入到 $ {L}_{c} $ 中，向 $ {A}_{2} $ 发送 $ {k}_{\text{u}{\text{p}}_{i}}= $ $ \left({X}_{i},{R}_{i}\right) $ ；若 $ {I}{{D}}_{i}={I}{{D}}_{A} $ ，选择随机数 $ {r}_{i}\in {Z}_{q}^{*} $ ，计算 $ {R}_{i}={r}_{i}\cdot P $ ， $ {X}_{i}={x}_{i}\cdot P $ ，将 $ \left({I}{{D}}_{i},{R}_{i},\perp ,\perp ,{X}_{i}\right) $ 加入到 $ {L}_{c} $ 中（其中， $ \perp $ 表示空值），向 $ {A}_{2} $ 发送 $ {k}_{\text{u}{\text{p}}_{i}}=\left({X}_{i},{R}_{i}\right) $ 。

② $ {H}_{3} $ 询问。当 $ {A}_{2} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行 ${H}_{3}({m}_{i}, $ $ {I}{{D}}_{i},{K}_{i},{X}_{i})$ 询问时， $ C $ 检索 $ {L}_{{H}_{3}} $ ，若 $ {L}_{{H}_{3}} $ 中存在 $({I}{{D}}_{i},{R}_{i},{h}_{i}^{3}, $ $ {K}_{i})$ ，发送 $ {h}_{i}^{3} $ 给 $ {A}_{2} $ ；否则，选择随机 $ {h}_{i}^{3}\in {Z}_{q}^{*} $ ，并加入到 $ {L}_{{H}_{3}} $ 中，向 $ {A}_{2} $ 发送 $ {h}_{i}^{3} $ 。

③秘密值询问。当 $ {A}_{2} $ 对身份为 $ {I}{{D}}_{i} $ 的用户进行秘密值询问时，若 $ {I}{{D}}_{i}={I}{{D}}_{A} $ ， $ C $ 终止；否则，检索 $ {L}_{c} $ ，若 $ {L}_{c} $ 中存在 $ \left({I}{{D}}_{i},{R}_{i},{d}_{i},{x}_{i},{X}_{i}\right) $ ，发送 $ {x}_{i} $ 给 $ {A}_{2} $ ；否则，执行公钥生成算法，向 $ {A}_{2} $ 发送 $ {x}_{i} $ 。

④私钥询问。与敌手 $ {A}_{1} $ 的私钥询问过程相同。

⑤标签生成询问。当 $ {A}_{2} $ 对身份 $ {I}{{D}}_{i} $ 、数据块 $ {m}_{i} $ 进行标签生成询问时， $ C $ 计算 $ {h}_{i}^{1} $ 、 $ {h}_{i}^{2} $ 和 $ {S}_{i} $ ，获得标签 ${\sigma }_{i}= $ $ \left({K}_{i},{S}_{i}\right)$ ，然后将 $ {m}_{i} $ 和 $ {\sigma }_{i}=\left({K}_{i},{S}_{i}\right) $ 发送给 $ {A}_{2} $ ，并在列表 $ {L}_{I} $ 中记录身份消息 $ {I}{{D}}_{i} $ 。

伪造：与敌手 $ {A}_{1} $ 的伪造过程相同。由分叉引理可知，选择不同的哈希函数 $ {H}_{3} $ 与 $ {H}_{3}' $ ,能够得到额外的有效伪造标签 $ {\sigma }'=\left(K,{S}'\right) $ ，则有：

$\qquad \qquad \left\{ \begin{array}{l} S={x}_{A}{h}_{A}^{3}+{r}_{A}+{k}_{\text{ms}} {h}_{A}^{1}+{k}_{A} {h}_{A}^{2},\\ {S'}={x}_{A}{h_{A}^{3}}'+{r}_{A}+{k}_{\text{ms}} {h}_{A}^{1}+{k}_{A} {h}_{A}^{2} \end{array}\right.$

(14)

计算得 ${x}_{A}=\dfrac{S-{S}'}{{h}_{A}^{3}-{{h}_{A}^{3}}'}$ ，则 $ C $ 可以利用 $ {A}_{2} $ 解决ECDLP。

定义事件 $ {E}_{1} $ ： $ {A}_{2} $ 在询问过程中不终止；事件 $ {E}_{2} $ ： $ {A}_{2} $ 在伪造过程中不终止；事件 $ {E}_{3} $ ： $ {A}_{2} $ 成功输出两个有效标签。则概率 $ P\left({E}_{1}\right) $ 和 $ P\left({E}_{2}\right) $ 分别为：

$ {\;\;\;\;\;\;\;\;\;\;\;P\left({E}_{1}\right)\ge {\left(1-\frac{1}{{q}_{2}+{q}_{3}+1}\right)}^{{q}_{2}+{q}_{3}}} $

(15)

$ P\left({E}_{2}\right)=\frac{1}{{q}_{2}+{q}_{3}+1} $

(16)

假设 $ {A}_{2} $ 输出的签名有效的概率为 $ \varepsilon $ ，则 $ P\left({E}_{3}\right) $ 为：

$ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;P\left({E}_{3}\right)\ge \frac{1}{e}\frac{1}{{q}_{2}+{q}_{3}+1}\left(1-\frac{1}{e}\right)\frac{1}{{q}_{{H}_{3}}}\varepsilon }$

(17)

若 $\varepsilon$ 不可忽略，则 $ C $ 能够以大于 $[1/e({q}_{2}+{q}_{3}+1\left)\right]\cdot $ $ (1-1/e)\cdot (1/{q}_{{H}_{3}})\cdot \varepsilon$ 的概率成功解决ECDLP。

3.3 隐私保护

用户持有私钥 $ {k}_{\text{us}}=(x,d) $ ， $ x $ 由用户自身产生， $ d $ 由KGC根据用户的ID产生，针对KGC实现了私钥的隐私保护，能够解决密钥托管问题。若TPA或云端试图利用标签计算用户私钥 $ x $ 、 $ d $ ，则需要解决ECDLP，因此，无法计算用户私钥。云端存储数据块 $ {m}_{i} $ ，在 $ \text{VerifyProof} $ 阶段，TPA接受云端发送的数据块 $ {m}_{i} $ ，云端和TPA虽然持有数据块，但由于数据块 $ {m}_{i} $ 被加密算法E盲化，所以无法获取真正的内容信息。

4 效率分析

对方案的效率进行数值分析与实验验证，并从计算开销角度，将本方案与现有各无证书云审计方案进行了对比。

利用JPBC库进行实验，选取JPBC库中的 $ \text{TypeA} $ 型素数阶椭圆曲线。定义 $ {G}_{1} $ 为椭圆曲线点群， $ {G}_{2} $ 为乘法循环群，在 $ 64\;\text{bit} $ 、Windows 10操作系统、2.50 GHz、i5处理器、4 GB内存条件下，执行本方案审计过程中出现的各种运算10 000次，取平均时间开销，如表1所示。

表1 各运算平均时间开销 Tab. 1 Average time cost of each operation

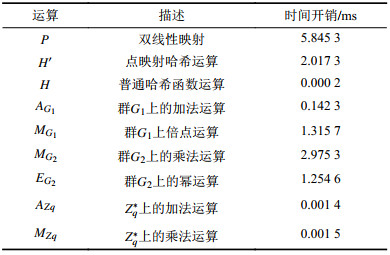对本方案的计算开销进行数值分析，在 $ \text{TagGen} $ 阶段，用户计算 $ {K}_{i}={k}_{i}\cdot P $ 与式（1）～（3），计算开销为 $ 2nH+2n{A}_{Zq}+2n{M}_{Zq }+n{M}_{{G}_{1}} $ 。在 $ \text{ProofGen} $ 阶段，云端计算 $S={\displaystyle\sum _{j=1}^{c}}{S}_{{i}_{j}}$ ，计算开销为 $ (c-1){A}_{{G}_{1}} $ 。在 $ \text{VerifyProof} $ 阶段，TPA计算式（1）、（2），并验证式（4），计算开销为 $ (2c-2)H+3{A}_{{G}_{1}}+3{M}_{{G}_{1}}+{M}_{Zq} $ 。对本方案与各文献方案在各阶段的计算开销进行数值对比分析，如表2所示。表2中， $ n $ 为数据块总数， $ c $ 为挑战数据块数量。

表2 各方案在不同阶段的计算开销对比 Tab. 2 Calculation cost comparison of each scheme in different stages

方案	TagGen	ProofGen	VerifyProof
文献[6]方案	$n{H}{ {'} }+2n{E}_{ {G}_{2} }+ 2n{M}_{ {G}_{1} }\approx \text{7.157 9}n$	$\begin{array}{l}(c-1){M}_{ {G}_{2} }+c{E}_{ {G}_{2} } +(c-1){A}_{Zq}+\\ \quad c{M}_{Zq}\approx 4.232\;8c-2.976\;7\end{array}$	$\begin{array}{l}3P+(c+1)H{'}+ (2c-1){M}_{ {G}_{2} }+\\ \quad(2c+1){E}_{ {G}_{2} } \approx 10.477\;1c+0.296\;6\end{array}$
文献[7]方案	$\begin{array}{l}(n+1)H{'}+H+n{A}_{ {G}_{1} } +2n{M}_{ {G}_{1} }+\\ \quad{A}_{Zq}+{M}_{Zq} \approx 4.791n+2.020\;2\end{array}$	$\begin{array}{l}(c-1){A}_{ {G}_{1} }+c{M}_{ {G}_{1} } +(c-1){A}_{Zq}+\\ \quad c{M}_{Zq} \approx 1.461\;8c-0.143\;7\end{array}$	$\begin{array}{l}2P+(c+1)H{'}+2H +(c+2){A}_{ {G}_{1} }+\\ \quad(c+3){M}_{ {G}_{1} } \approx 3.475\;3c+17.939\;6\end{array}$
文献[11]方案	$\begin{array}{l}(n+1){H}{ {'} }+nH+ 2n{A}_{ {G}_{1} }+4n{M}_{ {G}_{1} }+\\ \quad n{A}_{Zq}\approx 7.566\;1n+2.017\;3\end{array}$	$\begin{array}{l}H+(c-1){A}_{ {G}_{1} }+(c+1){M}_{ {G}_{1} } +\\ \quad c{A}_{Zq}+(c+1){M}_{Zq}\approx 1.460\;9c+1.174\;9\end{array}$	$\begin{array}{l}4P+cH{'}+(c+1)H+2c{A}_{ {G}_{1} } +(2c+3){M}_{ {G}_{1} }+\\ \quad(c-1){A}_{Zq} + c{M}_{Zq}\approx 4.936\;2c+27.329\;7\end{array}$
文献[12]方案	$\begin{array}{l}nH{'}+n{A}_{ {G}_{1} }+ 2n{M}_{ {G}_{1} }+\\ \quad{A}_{Zq} \approx 4.791n+0.001\;4\end{array}$	$\begin{array}{l}2H+(c-1){A}_{ {G}_{1} }+(c+1){M}_{ {G}_{1} } +c{A}_{Zq}+\\ \quad(c+1){M}_{Zq} \approx 1.460\;9c+1.174\;9\end{array}$	$\begin{array}{l}2P+(c+1)H{'}+2H +(c+3){A}_{ {G}_{1} }+\\ \quad(c+2){M}_{ {G}_{1} } \approx 3.475\;3c+16.766\;2\end{array}$
文献[16]方案	$\begin{array}{l}3H{'}+nH+4{A}_{ {G}_{1} } +(3n+3){M}_{ {G}_{1} }\approx\\ \quad 3.947\;1n+10.568\;2\end{array}$	$\begin{array}{l}(2c-2){A}_{ {G}_{1} }+2c{M}_{ {G}_{1} } +(c-1){A}_{Zq}+\\ \quad c{M}_{Zq} \approx 2.918\;9c-0.286\end{array}$	$\begin{array}{l}4P+5H{'}+cH+2{A}_{ {G}_{1} } +5{M}_{ {G}_{1} }+\\ \quad(2c-2){A}_{Zq} +c{M}_{Zq}\approx 0.004\;3c+40.328\end{array}$
本方案	$\begin{array}{l} 2nH+2n{A}_{Zq}+2n{M}_{Zq} +\\ \quad n{M}_{ {G}_{1} }\approx 1.321\;5n \end{array}$	$(c-1){A}_{ {G}_{1} }\approx 0.142\;3c-0.142\;3$	$\begin{array}{l}(2c-2)H+3{A}_{ {G}_{1} }+3{M}_{ {G}_{1} }+\\ \quad{M}_{Zq}\approx 0.000\;4c+4.375\;5\end{array}$

由表2可以看出：在 $ \text{TagGen} $ 阶段，文献[6,11]方案的计算开销约为本方案的6倍，文献[7,12,16]方案的计算开销约为本方案的3倍，故本方案对用户更加友好，且能够应用于算力较低的设备，在设计上更加合理高效。在 $ \text{ProofGen} $ 与VerifyProof阶段，本方案的计算开销也明显小于其他方案，在挑战数据块数量c逐渐增加的情况下，其他方案的计算开销增加的速度和幅度与本方案相比更加剧烈，故本方案的优势更加显著。

为了测试本方案在实际应用中的性能，且更直观地对比各方案的计算开销，在实验环境下运行各方案，设定数据块大小为2 kB，记录各方案在TagGen、ProofGen、VerifyProof阶段的时间开销数据，根据数据绘制图2～4。在数据块总数 $ n $ 变化的情况下，各方案在 $ \text{TagGen} $ 阶段的时间开销如图2所示。由图2可知，各方案在TagGen阶段的时间开销都与n约成正比关系，其中本方案对应的折线斜率最小，说明本方案效率最高。在挑战块数量 $ c $ 变化的情况下，各方案在 $ \text{ProofGen} $ 、 $ \text{Verifyproof} $ 阶段的时间开销如图3、4所示。由图3～4可知：本方案的时间开销仍然是各方案中最小的，而且随着挑战数据块数量c的增加，本方案在ProofGen、VerifyProof阶段的时间开销仅有少量增加，增加程度明显小于其余各方案。图2～4证实了表2在各阶段的数值分析。

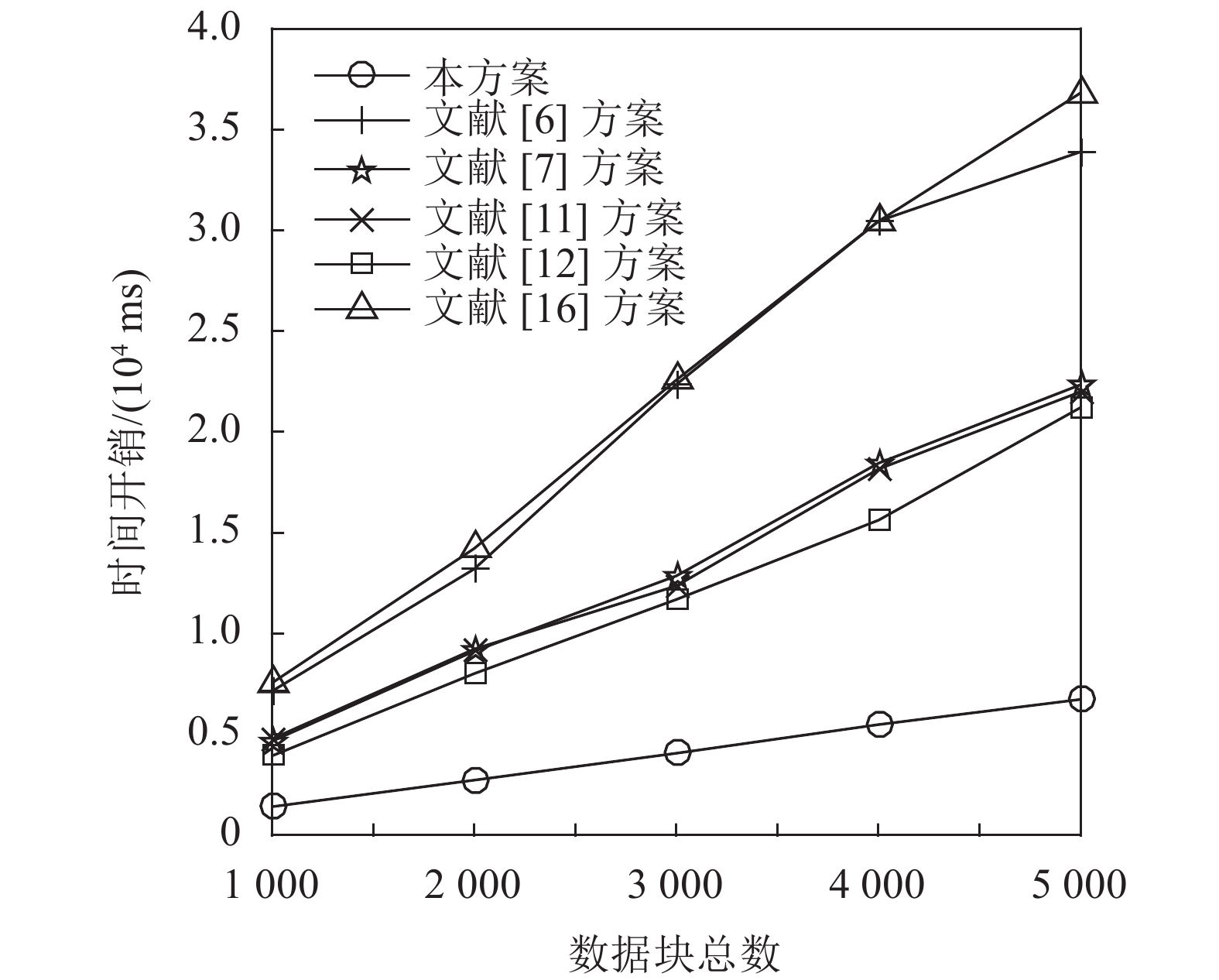图2 TagGen阶段时间开销对比 Fig. 2 Comparison of time cost in TagGen

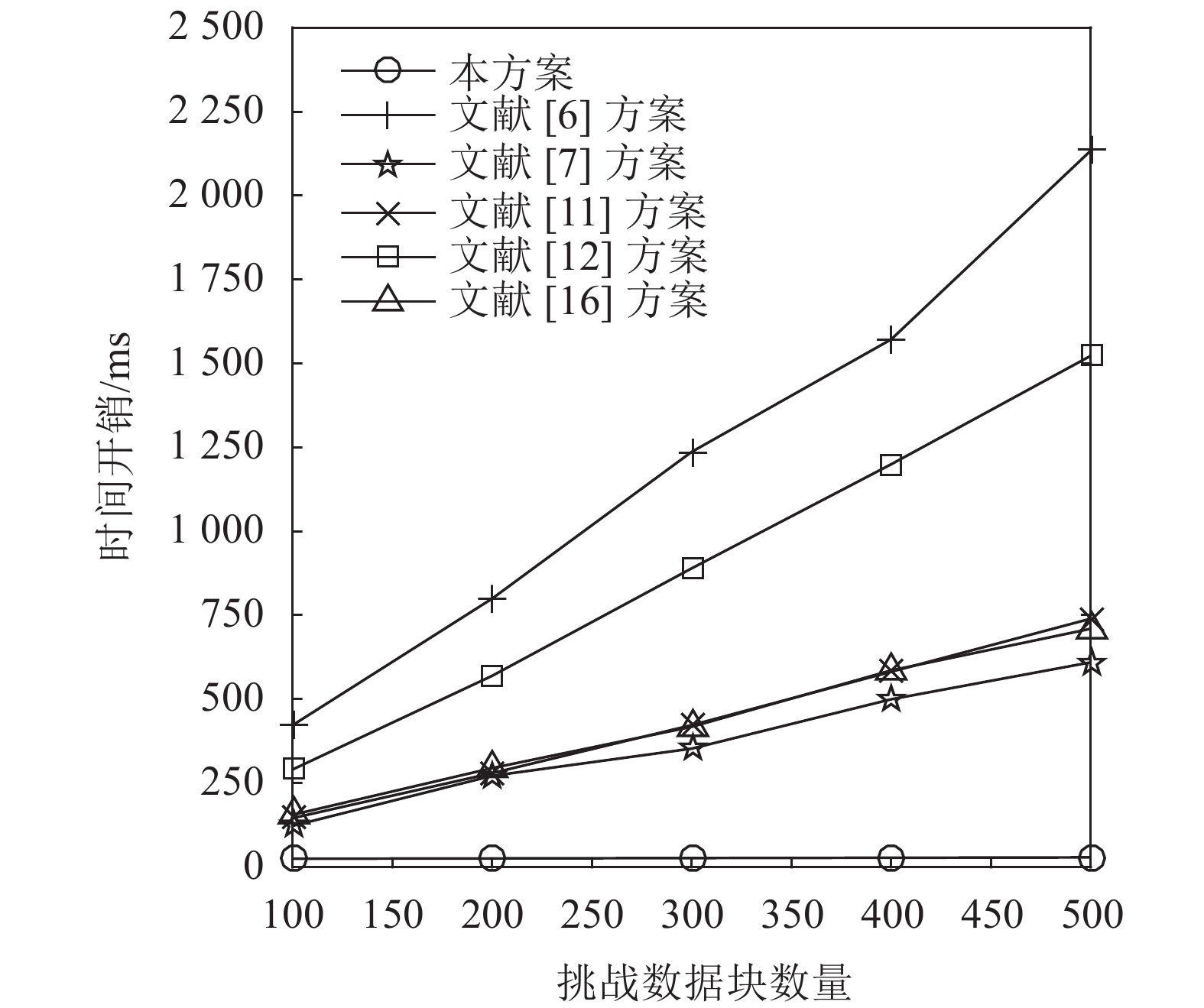图3 ProofGen阶段时间开销对比 Fig. 3 Comparison of time cost in ProofGen

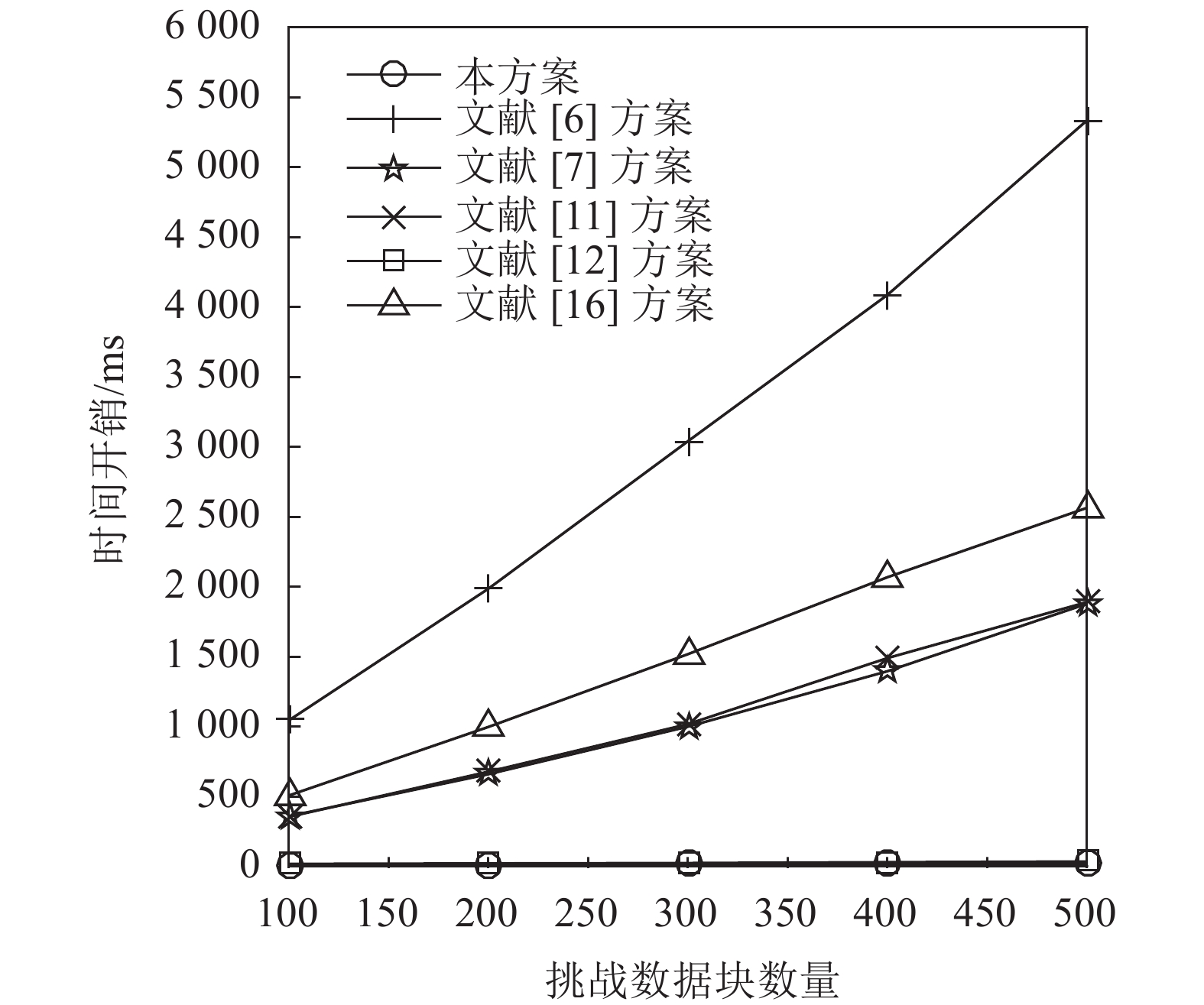图4 VerifyProof阶段时间开销对比 Fig. 4 Comparison of time cost in VerifyProof

5 结束语

针对现有云审计方案中存在的证书管理问题和密钥托管问题，以及现有无证书云审计方案安全性不足且审计效率较低的问题，设计了一种安全高效的无证书云审计方案。本方案在正确验证云端数据完整性的基础上，能够实现高效的动态更新功能，支持数据内容隐私保护，降低了计算、通信开销，且更加安全。下一步研究将结合区块链技术或格密码技术，为云审计方案增加更多功能，以适应未来更加复杂的需求。

参考文献

[1]	Singh B,Dhawan S,Arora A,et al. A view of cloud computing[J]. International Journal of Computers & Technology, 2005, 4(2): 387-392. DOI:10.24297/ijct.v4i2b1.3226
[2]	Quick D,Martini B,Choo K K R.Cloud storage forensics[M].Oxford:Syngress,2014:13–15.
[3]	Ateniese G,Burns R,Curtmola R,et al.Provable data possession at untrusted stores[C]//Proceedings of the 14th ACM Conference on Computer and Communications Security—CCS’07.New York:ACM,2007:598–609.
[4]	Wang Huaqun,Wu Qianhong,Qin Bo,et al. Identity-based remote data possession checking in public clouds[J]. IET Information Security, 2014, 8(2): 114-121. DOI:10.1049/iet-ifs.2012.0271
[5]	Shamir A.Identity-based cryptosystems and signature schemes[M]//Advances in Cryptology—CRYPTO 1984.Heidelberg:Springer,1985:47–53.
[6]	Wang Boyang,Li Baochun,Li Hui,et al.Certificateless public auditing for data integrity in the cloud[C]//Proceedings of the 2013 IEEE Conference on Communications and Network Security.National Harbor:IEEE,2013:136–144.
[7]	He Debiao,Zeadally S,Wu Libing. Certificateless public auditing scheme for cloud-assisted wireless body area networks[J]. IEEE Systems Journal, 2018, 12(1): 64-73. DOI:10.1109/JSYST.2015.2428620
[8]	Yang Hongbin,Jiang Shuxiong,Shen Wenfeng,et al. Certificateless provable group shared data possession with comprehensive privacy preservation for cloud storage[J]. Future Internet, 2018, 10(6): 49. DOI:10.3390/fi10060049
[9]	Ming Yang,Shi Wenchang. Efficient privacy-preserving certificateless provable data possession scheme for cloud storage[J]. IEEE Access, 2019, 7: 122091-122105. DOI:10.1109/ACCESS.2019.2938528
[10]	Huang Longxia,Zhou Junlong,Zhang Gongxuan,et al. Certificateless public verification for data storage and sharing in the cloud[J]. Chinese Journal of Electronics, 2020, 29(4): 639-647. DOI:10.1049/cje.2020.05.007
[11]	Kang Baoyuan,Wang Jiaqiang,Shao Dongyang. Certificateless public auditing with privacy preserving for cloud-assisted wireless body area networks[J]. Mobile Information Systems, 2017, 2017: 2925465. DOI:10.1155/2017/2925465
[12]	He Debiao,Kumar N,Wang Huaqun,et al. Privacy-preserving certificateless provable data possession scheme for big data storage on cloud[J]. Applied Mathematics and Computation, 2017, 314: 31-43. DOI:10.1016/j.amc.2017.07.008
[13]	Liao Yongjian,Liang Yikuan,Oyewole A W,et al. Security analysis of a certificateless provable data possession scheme in cloud[J]. IEEE Access, 2019, 7: 93259-93263. DOI:10.1109/ACCESS.2019.2928032
[14]	Ji Yanyan,Shao Bilin,Chang Jinyong,et al. Privacy-preserving certificateless provable data possession scheme for big data storage on cloud,revisited[J]. Applied Mathematics and Computation, 2020, 386: 125478. DOI:10.1016/j.amc.2020.125478
[15]	Wu Ge,Mu Yi,Susilo W,et al. Privacy-preserving certificateless cloud auditing with multiple users[J]. Wireless Personal Communications, 2019, 106(3): 1161-1182. DOI:10.1007/s11277-019-06208-1
[16]	Zhang Yuan,Xu Chunxiang,Yu Shui,et al. SCLPV:Secure certificateless public verification for cloud-based cyber-physical-social systems against malicious auditors[J]. IEEE Transactions on Computational Social Systems, 2015, 2(4): 159-170. DOI:10.1109/TCSS.2016.2517205
[17]	He Debiao,Kumar N,Zeadally S,et al. Certificateless provable data possession scheme for cloud-based smart grid data management systems[J]. IEEE Transactions on Industrial Informatics, 2018, 14(3): 1232-1241. DOI:10.1109/TII.2017.2761806
[18]	Galbraith S D,Paterson K G,Smart N P. Pairings for cryptographers[J]. Discrete Applied Mathematics, 2008, 156(16): 3113-3121. DOI:10.1016/j.dam.2007.12.010
[19]	Wang Cong,Chow S S M,Wang Qian,et al. Privacy-preserving public auditing for secure cloud storage[J]. IEEE Transactions on Computers, 2013, 62(2): 362-375. DOI:10.1109/TC.2011.245
[20]	Jin Zhengping.Research on the key escrow problem in identity based cryptosystem[D].Beijing:Beijing University of Posts and Telecommunications,2010. 金正平.基于身份的密码体制中密钥托管问题的相关研究[D].北京:北京邮电大学,2010.
[21]	Al–Riyami S S,Paterson K G.Certificateless public key cryptography[M]//Advances in Cryptology—ASIACRYPT 2003.Heidelberg:Springer,2003:452–473.
[22]	Miller V.Use of elliptic curves in cryptography[M]//Advances in Cryptology—CRYPTO’85 Proceedings.Heidelberg:Springer,1986:417–426.
[23]	Koblitz N. Elliptic curve cryptosystems[J]. Mathematics of Computation, 1987, 48(177): 203-209. DOI:10.1090/s0025-5718-1987-0866109-5
[24]	Hu Bingjie,Zhou Yanwei,Yang Bo,et al. Secure and efficient certificateless signature scheme without bilinear parings[J]. Journal of Yunnan University(Natural Sciences Edition), 2021, 43(3): 462-469. [胡冰洁,周彦伟,杨波,等. 安全高效的无双线性对的无证书签名方案[J]. 云南大学学报(自然科学版), 2021, 43(3): 462-469. DOI:10.7540/j.ynu.20200026]
[25]	Han Jing,Li Yanping,Yu Yong,et al. Cloud auditing scheme with dynamic revocation of users and real-time updates of data[J]. Journal of Software, 2020, 31(2): 578-596. [韩静,李艳平,禹勇,等. 用户可动态撤销及数据可实时更新的云审计方案[J]. 软件学报, 2020, 31(2): 578-596. DOI:10.13328/j.cnki.jos.005633]
[26]	杨波.现代密码学[M].3版.北京:清华大学出版社,2015.


工程科学与技术 2022, Vol. 54 Issue (3): 72-79