2. 中国科学院大学,北京 100049;
3. 云南交投集团公路建设有限公司,云南 昆明 650100;
4. 湖北省地质局第八地质大队,湖北 襄阳 441000
2. Univ. of Chinese Academy of Sciences, Beijing 100049, China;
3. Yunnan Communications Investment Group Highway Construction Co. Ltd., Kunming 650100, China;
4. Eighth Geological Brigade of Hubei, Xiangyang 441000, China
自然灾害事件的发生和发展并非彼此独立,相继发生的灾害在时间和空间上都存在着一定关联。由一种灾害引发或导致另外一种灾害发生,从而使得灾害的发生具有链式效应,这样的灾变现象称为灾害链[1]。
滑坡—堵江—堰塞湖灾害链是高山峡谷地区典型的灾害链形式,例如:2018年10月11日和11月3日,西藏白格村金沙江右岸发生了两次大规模高位滑坡,先后堵塞金沙江形成堰塞湖,后期堰塞体溃决形成的下泄洪水给下游四川、云南造成了严重的洪涝灾害[2]。相比于单一滑坡灾害而言,滑坡—堵江—堰塞湖灾害链的危险性通过时空上的延拓而大幅增加。然而,由于灾害之间链生关系的复杂性及当前研究方法的局限性,目前仍缺乏针对链生灾害的深入研究。
灾害成链的关键在于承灾体之间的能量传递,对于滑坡—堵江—堰塞湖这一灾害链形式,滑坡与水体间复杂的流–固耦合作用作为灾害链的衔接过程,往往决定了后续灾害的影响规模。其中,水以不同形式参与到灾害链的全过程,以自由水形式存在的江河、水库与海洋,以及入渗到滑坡体中的孔隙水,为模型的建立及灾害的精细化分析带来困难。
传统网格方法,如有限单元法,在模拟滑坡等大位移和大变形问题时存在网格畸变问题,水体的翻腾和破碎现象具有高度的非线性,基于网格的经典流体动力学方法很难进行建模与模拟。相比之下,无网格方法的优势明显,诸如:SPH为代表的无网格粒子类方法[3-5]、DDA方法[6,7],DEM–SPH为代表的离散元–无网格耦合方法[8-10]均得到了广泛的应用。其中,物质点法(MPM)作为一种兼具欧拉和拉格朗日描述的计算方法,综合了传统网格类方法和无网格方法的优势,二十多年来广泛应用于模拟滑坡失稳[11-16]、流体流动[17-19]及流–固耦合[20-24]等复杂力学问题上。然而,传统的MPM只能独立地模拟滑坡或水体,不适用于模拟滑坡堵江过程中的复杂流–固耦合问题。近年来发展的两相双质点格式的MPM通过对固相与液相分开建模,可将自由水、孔隙水在统一的框架下进行显式表达[25]。
本文针对滑坡堵江灾害链生过程,在Pradhana[26]发展的两相双质点物质点法(TPDP–MPM)的基础上,将TPDP–MPM拓展应用至地质灾害(链)的分析与评估中。通过模拟再现模型试验尺度下的Lituya滑坡体–水体相互作用过程,验证了TPDP–MPM在处理复杂流–固耦合问题方面的能力。在此基础上,对2011年湖北十堰二荒村滑坡堵塞平渡河灾害链生全过程进行计算模拟与分析,进一步丰富了滑坡堵江链生灾害方面的认识。
1 两相双质点MPM 1.1 物质点法的基本原理物质点法综合了网格类方法与无网格类方法的优势,将计算域视作一组物质点组成的连续体。每个质点(MPs)存储其代表区域的所有物理信息,如速度、质量、位移和其他量,通过形函数实现质点与背景网格节点(GNs)间信息的相互映射。如图1所示,允许代表实际计算域的 MPs(用红色圆点标记)自由移动,并在每一步累积映射自GNs的位移,而背景网格则在每一步结束后重置。
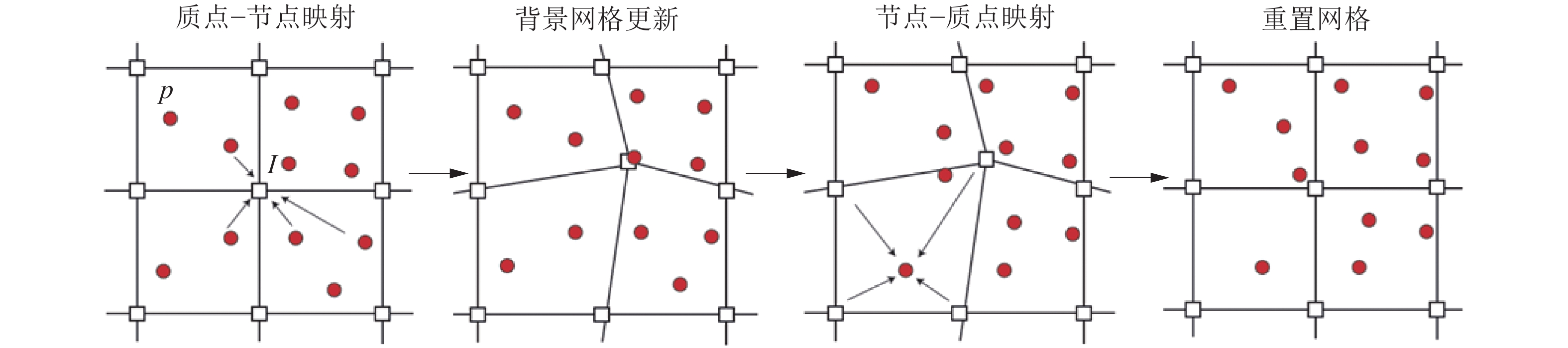 |
| 图1 物质点法计算流程 Fig. 1 Computational cycles of MPM |
在计算域
| $ \dot \rho + \rho \nabla \cdot {\boldsymbol{v}} = 0 $ | (1) |
| $ \rho \dot {\boldsymbol{v}} = \nabla \cdot \sigma + \rho b $ | (2) |
式(1)~(2)中,
由于质量信息储存在MPs上,因此,物质点法质量守恒自动满足。动量守恒的弱形式可以通过加权残差法推导出来。将任意试函数
| $ \int_\Omega {w\rho \dot {\boldsymbol{v}}{\rm{d}}\Omega } = \int_\Omega {\nabla w\sigma {\rm{d}}\Omega } + \int_\Omega {w\rho b{\rm{d}}\Omega } + \int_\Omega {w\tau {\rm{d}}S} $ | (3) |
式中,
通常,在流–固耦合力学问题中,水不仅作为孔隙中的耦合流体存在,而且作为自由流体存在,如河流、海洋和水库。两相双质点MPM通过对固相与液相分别建模,将自由水、孔隙水在统一的框架下进行显式地表达,如图2所示。
 |
| 图2 两相双质点MPM示意图 Fig. 2 Schematic diagram of two-phase double-point MPM approach |
对TPDP–MPM的固相速度–液相速度格式进行简要介绍,详细内容参考文献[25-28]。
饱和多孔介质的动力学行为同样用动量守恒方程来表述:
| $ {\rho ^\alpha }\frac{{{\rm{D}}{{\boldsymbol{v}}^\alpha }}}{{{\rm{D}}t}} = \nabla \cdot {\sigma ^\alpha } + {m^\alpha } + {\rho ^\alpha }g $ | (4) |
式中:
| $ \rho \frac{{{\rm{D}}{\boldsymbol{v}}}}{{{\rm{D}}t}} = \sum\limits_\alpha {{p^\alpha }\frac{{{\rm{D}}{{\boldsymbol{v}}^\alpha }}}{{{\rm{D}}t}}} $ | (5) |
对式(5)求和,可得到混合物的动量守恒方程:
| $ \rho \frac{{{\rm{D}}{\boldsymbol{v}}}}{{{\rm{D}}t}} = \nabla \cdot \sigma + \rho g $ | (6) |
式中,
Jassim等[25]所提出的重力驱动流中液相与固相的动量交换项
| $ {m^{\text{s}}} = - {m^{\text{f}}} = {c_{\text{E}}}({{\boldsymbol{v}}^{\text{f}}} - {{\boldsymbol{v}}^{\text{s}}}) + {p^{\text{f}}}\nabla {\varphi ^{\text{f}}} $ | (7) |
式中:
针对滑坡堵江灾害链特点,为克服使用水体真实状态方程而导致的时间积分步长过小的问题,将水体视作微可压缩流体,采用Becker等[30]提出的人工状态方程作为求解水体压强的控制方程:
| $ {\sigma ^{\text{f}}} = - {p^{\text{f}}}{\boldsymbol{I}} $ | (8) |
| $ {\psi ^{\text{f}}}({J^{\text{f}}}) = - B\left( {\frac{{{{({J^{\text{f}}})}^{1 - \gamma }}}}{{1 - \gamma }} - {J^{\text{f}}}} \right) $ | (9) |
| $ {p^{\text{f}}} = - \frac{{\partial {\psi ^{\text{f}}}}}{{\partial {J^{\text{f}}}}}({J^{\text{f}}}) $ | (10) |
| $ {p^{\text{f}}} = B[ {{{( {{J^{\text{f}}}} )}^\gamma } - 1} ] $ | (11) |
式(8)~(11)中,
此外,基于内接Mohr–Coulomb屈服面的Drucker–Prager准则建立岩土材料的弹塑性本构关系模拟滑坡体。
2 滑坡体–水体相互作用的方法验证利用两相双质点MPM法对Fritz开展的模型试验进行建模与模拟,模拟结果进一步证明了TPDP–MPM在涉及耦合问题的灾害链评估中良好的应用前景。
1958年7月8日,Gilbert海湾一侧山体在里氏8.3级地震作用下失稳,约3×107 m3滑坡体滑入Gilbert海湾,激起的涌浪在对岸山体的爬升高度高达524 m,图3为滑坡区域航拍照片。Fritz等[31]建立了模型试验尺度的Lituya滑坡概化模型,将实际滑坡按1∶675的比例进行了缩小。本文以模型试验尺度建立了数值计算模型,通过两套质点,将滑坡体离散为2 189个质点,将水体离散为5 877个质点,结构化背景网格尺寸为0.02 m,两相材料参数及其他输入参数见表1。
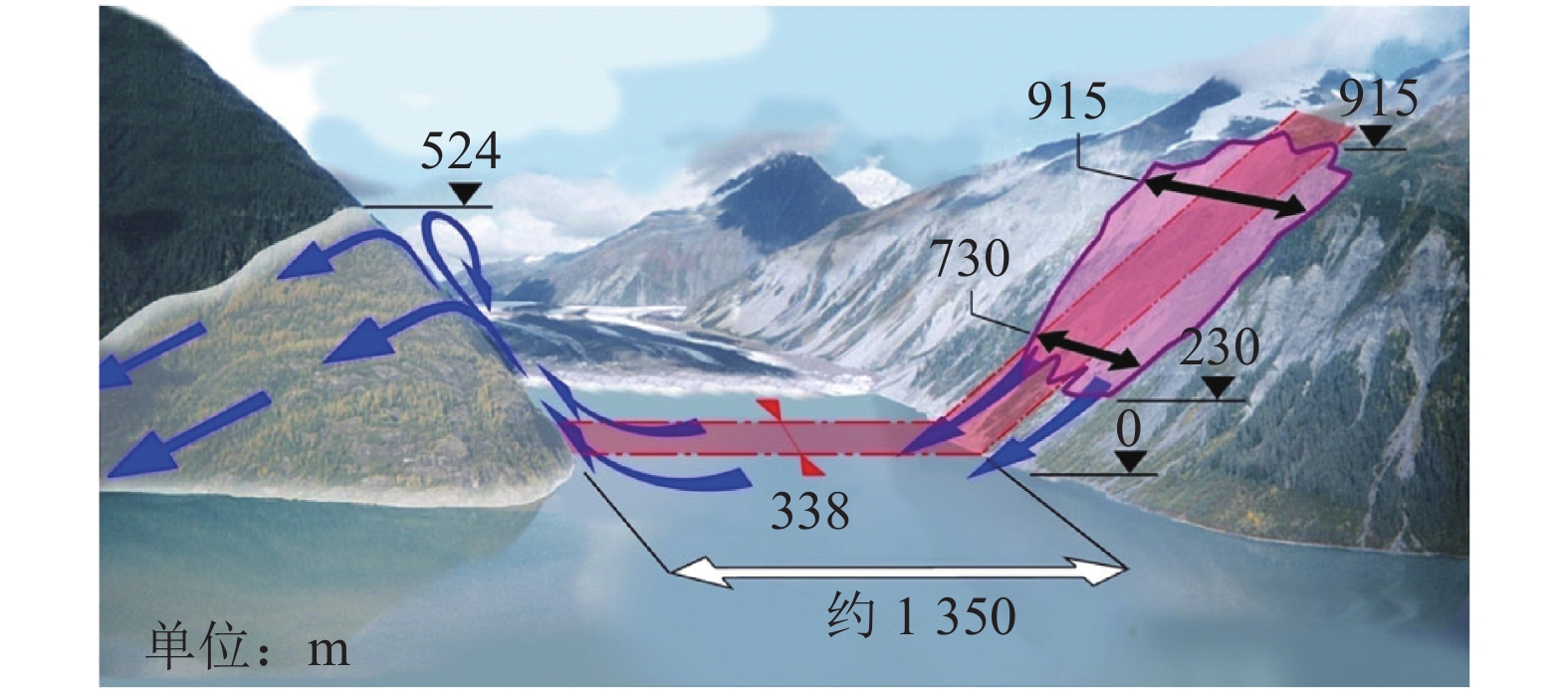 |
| 图3 Gilbert海湾Lituya滑坡航拍示意图 Fig. 3 Aerial photo of Lituya landslide in Gilbert inlet |
| 表1 计算参数 Tab. 1 Input parameters |
 |
在计算过程中实时记录滑坡诱发涌浪的运动,如图4所示。通过与Fritz模型试验结果对比发现,TPDP–MPM可以准确模拟滑坡体与水体相互作用及耦合过程,从而验证了TPDP–MPM在模拟复杂流–固耦合问题方面的能力。进一步地,可以将TPDP–MPM应用于高山峡谷地区广泛分布的滑坡堵江灾害链的力学分析与风险评估。
 |
| 注:左图为数值模拟结果,右图为试验结果;相邻两个图的时间间隔为0.133 18 s。 图4 滑坡诱发涌浪过程数值模拟与试验结果对比 Fig. 4 Comparing the numerical and experimental results of landslide induced surge process |
3 典型滑坡堵江灾害案例与仿真模型
二荒村滑坡[32]位于湖北省西北部房县南部山区,海拔高程大多在1 100~1 500 m之间,地形切割深度在400~1 000 m之间,属构造侵蚀剥蚀中低山地形。滑体所在平渡河河段自南东向北西径流,构成斜向河谷。河谷横断面呈“V”字形,河谷宽20~40 m,两岸地势陡峻,坡角35°~65°,局部呈陡崖。滑坡纵长约300 m,后缘宽50 m,前缘宽 150 m,滑体厚10~60 m,平均厚40 m,总滑动量15×104 m3。
2011年6月14日16时40分,湖北省十堰市房县上龛乡二荒村二组平渡河右岸山体发生滑坡,滑坡堆积体堵塞平渡河,形成堰塞湖。图5(a)为二荒村滑坡最终堆积并堵塞平渡河的现场照片。滑坡造成百户沟电站(装机容量7 200 kW)前池和部分压力管道毁坏,致使百户沟电站停止发电。二荒村滑坡地质剖面图如图5(b)所示,滑坡堆积体由巨石、碎块石、碎石土及粉质黏土等组成,杂乱无序堆积。巨石块度达3.0 m×2.0 m×1.5 m,块石直径一般为0.4~1.0 m,黏土所占比例较少,土石比约为1∶9。堆积体结构松散,空隙大,可见堰塞湖内水流从空隙中下泄。
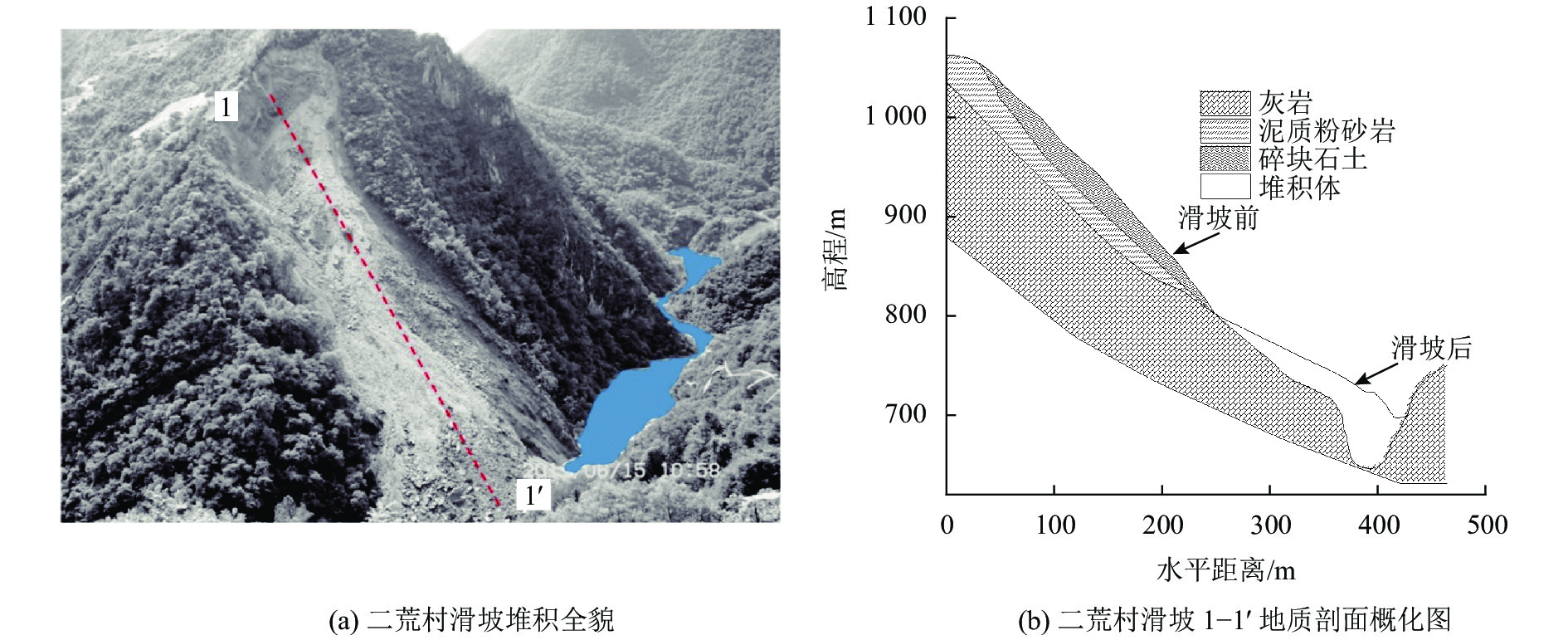 |
| 图5 二荒村滑坡概况 Fig. 5 Overall situation of Erhuang Village landslide |
通过两套质点分别对滑坡体与水体进行建模,如图6所示。地层自下而上依次为灰岩、泥质粉砂岩和粉质黏土夹杂碎块石。基于泊松采样技术,将滑坡体离散为2 491个质点,平渡河水体离散为1 172个质点,结构化背景网格尺寸为1.0 m。采用显示更新格式,参考材料经验与文献取值[13],确定两相材料参数,见表2。
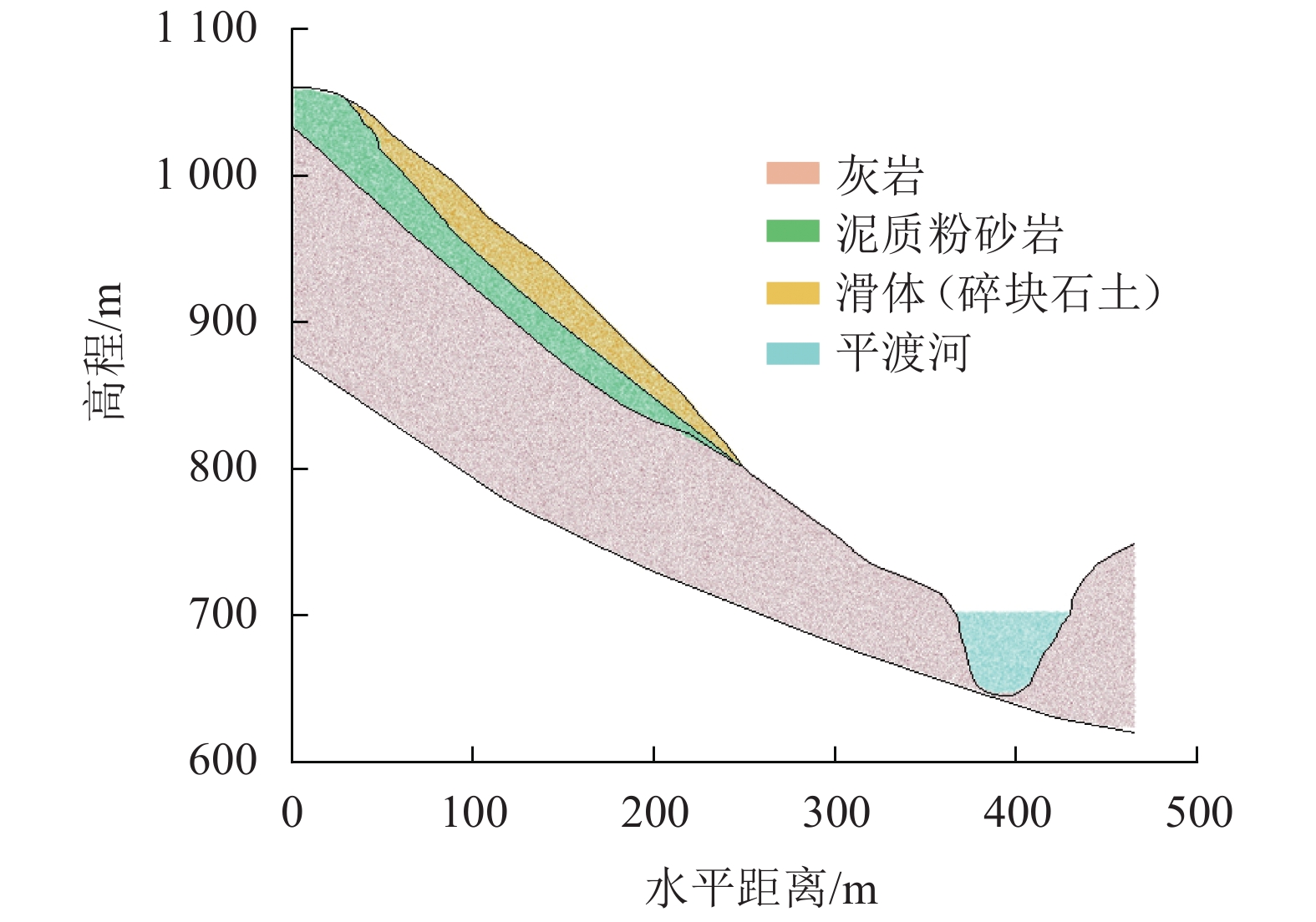 |
| 图6 二荒村滑坡仿真模型 Fig. 6 Numerical model of Erhuang Village landslide |
通过解除初始地应力约束实现二荒村滑坡的启动:根据地质勘察资料,二荒村滑坡的滑动面是明确的,以滑坡体的初始形状作为计算边界对滑坡体进行约束,输入偏大的强度参数计算滑坡体初始地应力;随后解除初始约束,给滑坡体赋以实际强度参数,使滑坡体进入不稳定状态后开始下滑[33]。
| 表2 计算参数 Tab. 2 Input parameters |
 |
4 滑坡堵江灾害链生全过程分析
图7为TPDP–MPM模拟得到的二荒村滑坡失稳堵塞平渡河的全过程持续约32.3 s间从滑坡启动t=0到最终堆积稳定t=32.3 s中的6个时刻的滑坡形态。由图7可以看出:初始时刻,在重力作用下,二荒村滑坡体启动下滑,滑坡体中后缘拉裂缝开始发育并向深部发展;12.5 s左右,滑坡体前缘到达平渡河水面后开始侵入河体,15.75 s时的模拟结果如图7(c)所示;15.8 s左右,滑坡体前缘撞击河谷后开始沿岸坡堆积;32.3 s左右,滑坡运动停止,如图7(f)所示,堆积体在靠近对岸岸坡的最低高程为697.2 m,平渡河水面高程为700 m,即二荒村滑坡几乎完全堵塞平渡河,并形成堰塞体。图8为TPDP–MPM计算得到的二荒村滑坡最终堆积形态与现场实际情况(图8中虚线)的对比,两者在轮廓上吻合良好。
 |
| 图7 二荒村滑坡失稳后运移—堵江全过程 Fig. 7 Whole process of migration and river blocking after failure of landslide |
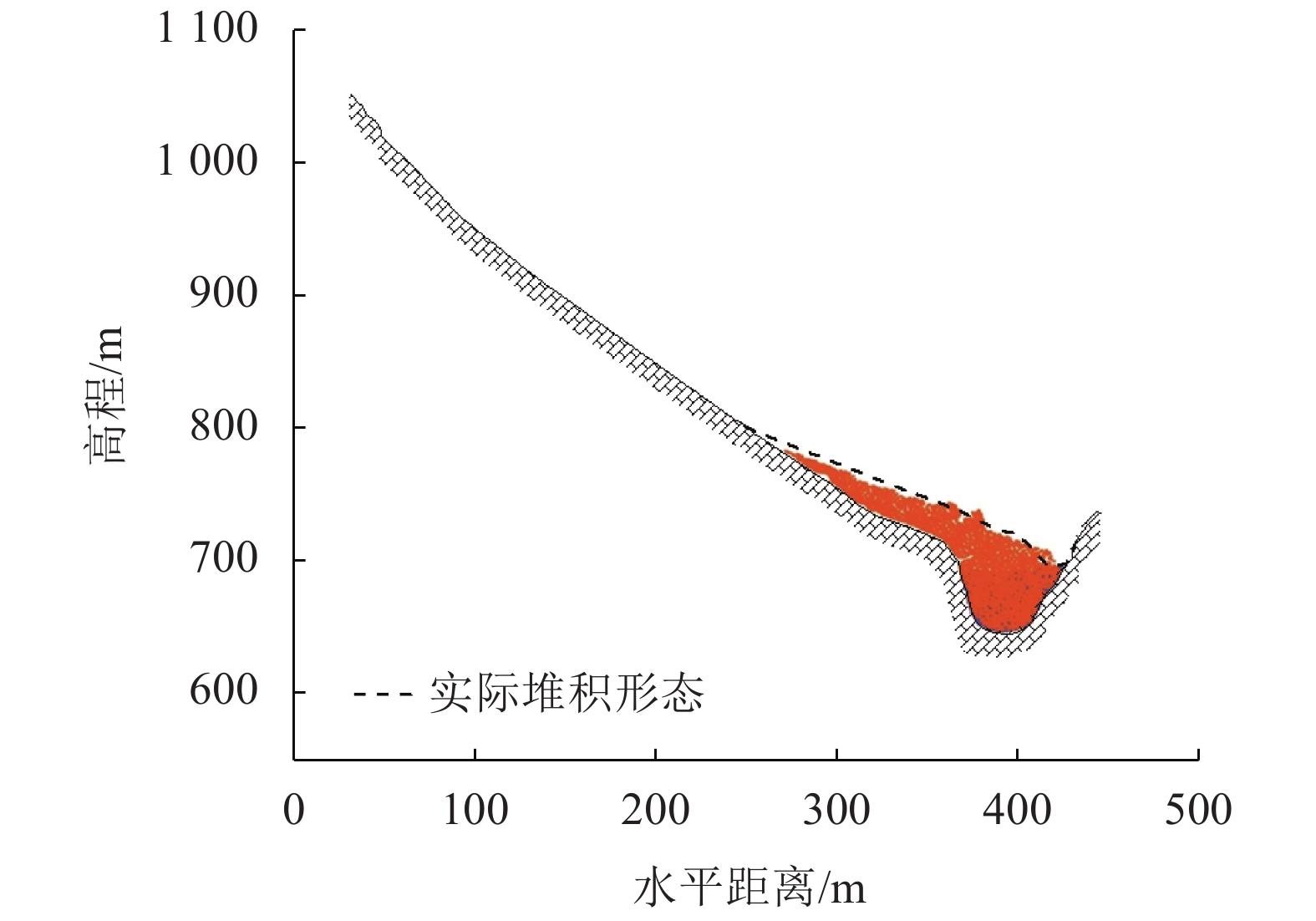 |
| 图8 滑坡最终堆积形态结果对比 Fig. 8 Final accumulation profile of landslide |
4.1 速度分布特征
不同时刻滑坡体速度场如图9所示。
 |
| 图9 滑坡体内部速度场演化 Fig. 9 Velocity field of the landslide mass |
根据滑坡失稳过程呈现的模式,将滑坡体沿滑动方向等分为前缘部分、中间部分与后缘部分(标记如图7(b)所示)。失稳滑动前期(t=0~9.8 s),在重力作用下,滑坡体中部及前缘开始滑动,并逐渐产生比后缘更高的速度;t=9.8 s时,前缘部分速度就达到了21.0 m/s。在这一阶段,滑坡后缘的运动始终滞后于滑坡前缘。
随着时间的推移,滑坡后缘与中前缘的速度差距进一步拉大,t=9.8 s后,后缘与中前缘连接处拉裂缝开始发展,如图9(b)所示。随着拉裂缝逐步向深部扩展,后缘“坡脚处”产生自由表面,由于约束减少,后缘开始加速下滑,此时滑坡后缘运移速度高于上一阶段的速度,滑坡趋于整体的高速运动。t=12.3 s时,滑坡体前缘开始由滑床抛出,如图9(c)所示,滑坡体质点速度进一步提高,在16.0 s左右,滑坡体入水速度达到了39.6 m/s。
此后,随着滑坡体前缘开始侵入水体,对比平渡河水面上下的滑坡体质点速度可以发现:入水部分的滑坡体在水体制动作用下速度开始大幅降低,如图9(e)所示。此后,滑坡整体向河谷内减速、堆积,直至t=32.3 s末,滑坡整体速度趋于0,此时滑坡体与平渡河水体均接近于稳定状态,堆积过程结束,如图9(h)所示。
4.2 能量演化规律图10为滑坡—堵江灾害全过程中的滑坡体质点动能、滑坡体总动能随时间的变化情况。由图10可知:滑坡由启动到前缘抵达河面前(0~11.9 s),滑坡动能快速提高,图10(a)中的两条曲线可以说明滑坡体前缘和后缘的动能演化规律,前期滑坡后缘动能始终低于前缘,后缘动能在6.2 s后开始与滑坡前缘以一致的增速增长;9.68 s左右,滑坡前缘到达临河缓坡区域后,前缘速度有所降低,如图9(b)所示,滑坡体总动能增长放缓,如图10(b)的范围Ⅲ所示;11.9 s滑坡前缘入江后,如图10(a)范围Ⅰ所示,质点速度的离散性增强,在水体制动作用下,滑坡体前缘入水部分的质点速度明显降低。随着入水滑坡体积的增大,水体制动作用越发显著,滑坡体总动能保持增长但趋势进一步放缓,如图10(b)中范围Ⅰ所示;15.8 s左右滑坡体前缘到达河谷前,滑坡体总动能达到峰值,滑坡体前缘撞击河谷后速度趋于0,滑坡体开始在河谷底部向上堆积,由于重力势能的减小,滑坡体总动能开始锐减,如图10(b)范围Ⅱ所示,直至32.3 s时完全堆积、静止。
 |
| 图10 滑坡体能量演化 Fig. 10 Energy evolution of landslide mass |
4.3 滑坡—堵江全过程分析
从TPDP–MPM模拟结果来看,二荒村滑坡在重力作用下启动,经历下滑过程中的加速、破裂解体后,滑坡体前缘侵入平渡河水体,并在撞击平渡河河谷后开始在谷底堆积,最终完全堵塞平渡河,形成方量巨大的堰塞体。滑坡—堵江全过程可分为4个阶段。
1)失稳启动
t=0~9.8 s时,在重力作用下,滑坡体的动能开始累积,滑坡体中前缘很快加速到10 m/s以上。在这一阶段,受制于中前缘的约束,滑坡后缘滑动速度滞后于中前缘,如图9(b)所示。
2)高速滑动
t=9.8~12.5 s时,随着中前缘与后缘速度差增加,在滑坡体后缘与中前缘连接处形成了拉裂缝,并向深部发展,滑坡体中前缘开始脱离后缘,约束减弱,后缘开始加速下滑,滑坡体趋于整体滑动。由于临河岸坡地形逐渐平缓,滑坡体前缘由滑床向河谷中央抛射,进一步提高了滑坡体前缘的入水速度。在这一阶段,滑坡表现为整体的高速滑动,如图9(c)所示。
3)入江制动
t=12.5~15.8 s时,滑坡前缘开始侵入水体,对比图9(d)平渡河水面上下的质点速度,以及图10(a)入水前后质点动能变化,可以发现:在水体撞击制动及流–固耦合耗散作用下,入水部分滑坡体动能显著降低;这一阶段,在中后缘持续的推动作用下,滑坡体依然整体向河谷高速滑移;但随着入水滑坡体积的增大,水体的制动作用越发明显,滑坡体总动能增长速度放缓。
4)堆积成坝
t=15.8~32.3 s时,随着滑坡体前缘开始碰撞河谷,质点速度急剧衰减并趋近于0,如图9(f)~(h)所示。滑坡体开始在河谷谷底沿岸坡向上堆积,随着重力势能减小,滑坡整体运移速度开始衰减,并在32.3 s左右滑坡整体堆积,形成堰塞坝堵江。
5 结论与展望为再现典型滑坡堵江链生灾害演化全过程,将两相双质点MPM扩展应用于地质灾害链的分析与评估中。以2011发生的湖北十堰二荒村滑坡为研究对象,利用两套质点分别对滑坡体与水体分别进行建模,模拟了二荒村滑坡堵江全过程,对滑坡启动、运移、入水制动及堆积堵江过程进行了运动学分析,得出以下结论:
1)通过两相双质点MPM模拟再现了二荒村滑坡堵塞平渡河的全过程,整个过程持续了32.3 s,计算得到的二荒村滑坡最终堆积形态与现场勘查形态大致相同,这也证明了TPDP–MPM在分析地质灾害链问题上的可靠性。
2)二荒村滑坡在重力作用下启动,经历下滑过程中的加速、破裂解体后,滑坡体前缘侵入平渡河水体,并在撞击平渡河河谷后在谷底堆积,最终完全堵塞平渡河形成堰塞坝。从TPDP–MPM模拟结果来看,二荒村滑坡失稳—堵江全过程可分为失稳启动、高速滑动、入江制动和堆积成坝4个阶段。
3)基于速度场分布揭示了滑坡体不同阶段的运移模式:在滑坡初始启动阶段,滑坡后缘的运动始终滞后于滑坡前缘;随着中前缘与后缘速度差的拉大,连接处拉裂缝开始发展;此后滑坡体后缘开始加速,滑坡趋于整体的高速运动。
4)质点动能及总动能演化规律揭示了水体制动效应对滑坡体堆积过程的影响:滑坡体入水后质点速度的离散性增强,滑坡体总动能保持增长但趋势放缓。随着入水滑坡体积的增大,水体的制动作用越发明显;随后滑坡体前缘撞击河谷后开始沿岸坡堆积,由于重力势能的减小,滑坡体总动能开始锐减直至最终堆积成坝。
受限于计算能力不足,本文仅进行了2维滑坡堵江灾害链生过程模拟,后续将引入针对性的岩土失效准则,针对滑坡启动机制、3维全过程模拟、高效并行计算等方面开展进一步研究。
| [1] |
Han Jinliang,Wu Shuren,Wang Huabin. Preliminary study on geological hazard chains[J]. Earth Science Frontiers, 2007, 14(6): 11-23. [韩金良,吴树仁,汪华斌. 地质灾害链[J]. 地学前缘, 2007, 14(6): 11-23. DOI:10.1016/S1872-5791(08)60001-9] |
| [2] |
Xu Qiang,Zheng Guang,Li Weile,et al. Study on successive landslide damming events of Jinsha River in Baige village on Octorber 11 and November 3,2018[J]. Journal of Engineering Geology, 2018, 26(6): 1534-1551. [许强,郑光,李为乐,等. 2018年10月和11月金沙江白格两次滑坡–堰塞堵江事件分析研究[J]. 工程地质学报, 2018, 26(6): 1534-1551. DOI:10.13544/j.cnki.jeg.2018-406] |
| [3] |
Antonios X,Steven L,Peter S,et al.Landslides and tsunamis predicted by incompressible SPH with application to the 1958 Lituya Bay event and idealised experiment[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,2017,473(2199):20160674.
|
| [4] |
Manenti S,Pierobon E,Gallati M,et al. Vajont disaster:Smoothed particle hydrodynamics modeling of the postevent 2D experiments[J]. Journal of Hydraulic Engineering, 2015, 142(4): 05015007. DOI:10.1061/(ASCE)HY.1943-7900.0001111 |
| [5] |
Yeylaghi S,Moa B,Buckham B,et al. ISPH modelling of landslide generated waves for rigid and deformable slides in Newtonian and non-Newtonian reservoir fluids[J]. Advances in Water Resources, 2017, 107: 212-232. DOI:10.1016/j.advwatres.2017.06.013 |
| [6] |
Fu Xiaodong,Sheng Qian,Li Guo,et al. Analysis of landslide stability under seismic action and subsequent rainfall:A case study on the Ganjiazhai giant landslide along the Zhaotong—Qiaojia road during the 2014 Ludian earthquake,Yunnan,China[J]. Bulletin of Engineering Geology and the Environment, 2020, 79: 5229-5248. DOI:10.1007/s10064-020-01890-z |
| [7] |
Fu Xiaodong,Sheng Qian,Du Wenjie,et al. Evaluation of dynamic stability and analysis of reinforcement measures of a landslide under seismic action:A case study on the Yanyangcun landslide[J]. Bulletin of Engineering Geology and the Environment, 2020, 79: 2847-2862. DOI:10.1007/s10064-020-01745-7 |
| [8] |
Wang Zhichao,Li Daming. Fluid-structure coupling algorithm based on SPH–DEM and application to simulate landslide surge[J]. Rock and Soil Mechanics, 2017, 38(4): 1226-1232. [王志超,李大鸣. 基于SPH–DEM流–固耦合算法的滑坡涌浪模拟[J]. 岩土力学, 2017, 38(4): 1226-1232. DOI:10.16285/j.rsm.2017.04.038] |
| [9] |
Xu Wenjie. Fluid-solid coupling method of landslide tsunamis and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 29(7): 1420-1433. [徐文杰. 滑坡涌浪流–固耦合分析方法与应用[J]. 岩石力学与工程学报, 2020, 29(7): 1420-1433. DOI:10.13722/j.cnki.jrme.2020.0061] |
| [10] |
Tan Hai,Chen Shenghong. A hybrid DEM–SPH model for deformable landslide and its generated surge waves[J]. Advances in Water Resources, 2017, 108: 256-276. DOI:10.1016/j.advwatres.2017.07.023 |
| [11] |
Li Xinpo,Wu Yong,He Siming,et al. Application of the material point method to simulate the post-failure runout processes of the Wangjiayan landslide[J]. Engineering Geology, 2016, 212(Complete): 1-9. DOI:10.1016/j.enggeo.2016.07.014 |
| [12] |
Yerro A,Soga K,Bray J D. Runout evaluation of Oso landslide with the material point method[J]. Canadian Geotechnical Journal, 2019, 56(9): 1307-1317. DOI:10.1139/cgj-2017-0630 |
| [13] |
Ying Chunye,Zhang Kun,Wang Zenian,et al. Analysis of the run-out processes of the Xinlu Village landslide using the generalized interpolation material point method[J]. Landslides, 2020, 18: 1519-1529. DOI:10.1007/s10346-020-01581-6 |
| [14] |
Xu Xiaorong,Jin Feng,Sun Qicheng,et al. Three-dimensional material point method modeling of runout behavior of the Hongshiyan landslide[J]. Canadian Geotechnical Journal, 2019, 56: 1318-1337. DOI:10.1139/cgj-2017-0638 |
| [15] |
Conte E,Pugliese L,Troncone A. Post-failure analysis of the Maierato landslide using the material point method[J]. Engineering Geology, 2020, 277: 105788. DOI:10.1016/j.enggeo.2020.105788 |
| [16] |
Li Xinpo,Tang Xiong,Zhao Shuxi,et al. MPM evaluation of the dynamic runout process of the giant Daguangbao landslide[J]. Landslides, 2020, 18: 1509-1518. DOI:10.1007/s10346-020-01569-2 |
| [17] |
Kularathna S,Soga K. Implicit formulation of material point method for analysis of incompressible materials[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 313: 673-686. DOI:10.1016/j.cma.2016.10.013 |
| [18] |
Liang Dongfang,Zhao Xuanyu,Martinelli M. MPM simulations of the interaction between water jet and soil bed[J]. Procedia Engineering, 2017, 175: 242-249. DOI:10.1016/j.proeng.2017.01.019 |
| [19] |
Zhang Fan,Zhang Xiong,Sze K Y,et al. Incompressible material point method for free surface flow[J]. Journal of Computational Physics, 2017, 330: 92-110. DOI:10.1016/j.jcp.2016.10.064 |
| [20] |
Du Wenjie,Sheng Qian,Fu Xiaodong,et al. Extensions of the two-phase double-point material point method to simulate the landslide-induced surge process[J]. Engineering Analysis with Boundary Elements, 2021, 133(12): 362-375. DOI:10.1016/j.enganabound.2021.09.020 |
| [21] |
Liu Xin,Wang Yu. Probabilistic simulation of entire process of rainfall-induced landslides using random finite element and material point methods with hydro-mechanical coupling[J]. Computers and Geotechnics, 2021, 132: 103989. DOI:10.1016/j.compgeo.2020.103989 |
| [22] |
Bandara S,Ferrari A,Laloui L. Modelling landslides in unsaturated slopes subjected to rainfall infiltration using material point method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(9): 1358-1380. DOI:10.1002/nag.2499 |
| [23] |
Wang B,Vardon P J,Hicks M A. Rainfall-induced slope collapse with coupled material point method[J]. Engineering Geology, 2018, 239: 1-12. DOI:10.1016/j.enggeo.2018.02.007 |
| [24] |
Liang Dongfang,Zhao Xuanyu,Soga K. Simulation of overtopping and seepage induced dike failure using two-point MPM[J]. Soils and Foundations, 2020, 60(4): 978-988. DOI:10.1016/j.sandf.2020.06.004 |
| [25] |
Jassim I,Stolle D,Vermeer P A. Two-phase dynamic analysis by material point method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(15): 2502-2522. DOI:10.1002/nag.2146 |
| [26] |
Pradhana A.Multiphase simulation using material point method[D].Los Angeles:University of California,2017.
|
| [27] |
Bandara S,Soga K. Coupling of soil deformation and pore fluid flow using material point method[J]. Computers and Geotechnics, 2015, 63: 199-214. DOI:10.1016/j.compgeo.2014.09.009 |
| [28] |
Abe K,Soga K,Bandara S. Material point method for coupled hydromechanical problems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(3): 1-16. DOI:10.1061/(ASCE)GT.1943-5606.0001011 |
| [29] |
Mackenzie–Helnwein P,Arduino P,Shin W,et al. Modeling strategies for multiphase drag interactions using the material point method[J]. International Journal for Numerical Methods in Engineering, 2010, 83: 295-322. DOI:10.1002/nme.2823 |
| [30] |
Becker M,Teschner M.Weakly compressible SPH for free surface flows[C]//Proceedings of the ACM SIGGRAPH/Eurograph Symp Comp Anim.The Eurographics Association,2007:1–8
|
| [31] |
Fritz H M,Hager W H,Minor H E. Lituya Bay case:Rockslide impact and wave run-up[J]. Science of Tsunami Hazards, 2001, 19(1): 3-19. |
| [32] |
国土资源部地质灾害应急技术指导中心.2011年度全国重大地质灾害事件与应急避险典型案例[M].北京:地质出版社,2012
|
| [33] |
Xu Xiaorong.Study on the flow process of granular materials with the material point method simulations and its engineering applications[D].Beijing:Tsinghua University,2018. 徐小蓉.颗粒介质流动过程的物质点法模拟及其工程应用[D].北京:清华大学,2018. |
 2022, Vol. 54
2022, Vol. 54


