Fresnel Field Phase Retrieval via High-speed Phase Modulation
-
摘要: 多强度相位恢复方法通过改变光学成像系统中的物理参数获得不同的编码衍射图案，无需额外的先验知识即可实现相位的最佳收敛和高精度重建，然而现有多强度相位恢复方法在获取不同测量值的过程中，往往需要不断改变成像系统的物理结构，需要精确移动或调整部分光学元件的空间位置，反复地对齐与校准显著增加了工作量，从而导致成像结构较为复杂。针对上述问题，本文提出基于高速相位调制的菲涅耳场编码衍射图案实时获取方法，该方法主要使用电可调透镜（ETL）或纯相位型硅基液晶（PLCoS）两种纯相位空间光调制器来进行相位的快速动态调制，通过自由空间传播到记录平面，由探测器获取强度信息，无需使用透镜装置或者改变成像系统的物理结构，最后使用WF算法从获取的多幅编码衍射图案中同时重建光场的振幅和相位。通过对远场（FF）和菲涅耳场（FrF）在不同迭代次数、不同掩膜数量、不同噪声水平以及不同算法下分别进行对比实验，验证了本文方法的有效性和鲁棒性。相比于传统多强度相位恢复方法，本文所提出的成像系统更为紧凑和简单，避免了反复对齐与校准的工作量，具有重要的应用潜力，尤其是电可调透镜（ETL）调制系统，可适用于高分辨率场景的高速记录。Abstract: The multi-intensity phase retrieval methods obtain different coded diffraction patterns by changing the physical parameters in the optical imaging system, which can achieve the best convergence of phase and high-precision reconstruction without additional prior knowledge. However, the existing multi-intensity phase retrieval methods often need to constantly change the physical structure of the imaging system and accurately move or adjust the spatial position of some optical elements in the process of obtaining different measurements. The repeated alignment and calibration significantly increase the workload, resulting in more complex imaging structure. To solve the above problems, a real-time acquisition method of Fresnel field coded diffraction pattern based on high-speed phase modulation was proposed in this paper. In the method, two pure phase spatial light modulators: electrically tunable lens (ETL) and pure phase silicon-based liquid crystal (PLCoS) were mainly used to perform the fast dynamic phase modulation. The phase was transmitted to the recording plane through free space, and the intensity information was obtained by the detector without using a lens or changing the physical structure of the imaging system. The WF algorithm was used to simultaneously reconstruct the amplitude and phase of the light field from multiple coded diffraction patterns. In the paper, the effectiveness and robustness of the proposed method were verified by the contrast experiments of farfield (FF) and Fresnel field (FrF) under different iteration times, different mask numbers, different noise levels and different algorithms. Compared with the traditional multi-intensity phase retrieval methods, the proposed imaging system is more compact and simple. It avoids the workload of repeated alignment and calibration, and has important application potentials. Especially, the electrically tunable lens (ETL) modulation scheme can be applied to high-speed recording of high-resolution scenes.
-
Keywords:
- multiple intensity /
- phase modulation /
- Fresnel field /
- phase retrieval
-
众所周知，描述光波场特性的主要物理量有振幅、波长和相位，研究表明大部分的信息被编码在相位中。由于可见光的振荡频率约为1015 Hz，现有的光学测量设备通常依赖于将光子转换成电子（电流），无法直接记录光场的相位信息，只能记录其振幅或强度信息。因此需要通过测量振幅或强度来恢复丢失的光场相位信息，即相位恢复（phase retrieval，PR）[1]。相位恢复问题在过去的几十年中得到了大量的研究，广泛应用于天文、光学和X射线等成像领域。
相位恢复是从复光场的傅里叶变换的振幅中恢复原复光场。相位恢复研究内容主要分为成像系统设计与相位恢复算法的设计。相位恢复算法主要可分为3大类：经典Gerchberg-Saxton-Fienup（GSF）类算法[2]、以PhaseLift为代表的凸优化方法[3]、以Wirtinger flow（WF）算法为代表的新一代非凸优化方法[4]。Candès等在2015年提出了一个基于WF的非凸优化算法[4]，先通过谱初始化获得初始估计，再通过梯度更新下降来迭代细化初始估计，并能以很高的概率确保收敛到全局的最优解。该算法不仅解决了传统GSF等类算法收敛速度慢、容易进入“停滞”状态的问题，也很轻松地克服了收敛到局部极小解的问题，同时，解决了PhaseLift等凸优化算法的计算复杂度过高，难以进行尺度较大的2维信号重建的问题。
本文主要研究的是成像系统的设计。根据相位恢复算法需要的强度图像数目的不同，可以分为：单强度相位恢复（single-intensity phase retrieval，SIPR）[5-8]、双强度相位恢复[5]（double-intensity phase retrieval，DIPR）和多强度相位恢复（multiple-intensity phase retrieval，MIPR）[9]。SIPR方法（包括GSF算法）仅需要单幅强度图像（例如，频域测量[10-11,5-6]），但通常需要引入额外的先验信息（prior knowledge）进行相位恢复，例如，非负性（nonnegativity）、支撑（support）约束、稀疏先验（sparsity）等[6-7]。SIPR和DIPR属于迭代相位恢复（iterative phase retrieval, IPR）方法，虽然在一定程度上可以恢复相位，但是，面临收敛速度较慢、易陷入“停滞”状态及无法保证唯一性 （non-uniqueness）等缺点。为了改进上述的不足，MIPR方法进行多幅强度图像的测量，因此通过使用不同的光学系统参数获取多幅强度图像以完成相位恢复。MIPR方法包括PhaseLift算法、WF算法、TWF（truncated Wirtinger flow）[8]、TAF（truncated amplitude flow）[12]算法等，主要通过改变光学成像系统中的物理参数获得不同多样性的测量值[13]，例如，多距离[14-15]、多掩膜[16]、多旋转角度[17]、多方向[18]、多平移[19-21]、多频率[22]等等。但是，上述方法在获取不同测量值的过程中往往需要不断改变成像系统的物理结构，如调制成像平面的位置、旋转透镜角度等，从而导致成像结构较为复杂，需要精确移动或调整部分光学元件的空间位置，反复地对齐与校准，增加了相应的工作量。
在相位恢复问题中，最常见的傅里叶测量对应的是远场（farfield，FF）测量或者在一个理想透镜的焦平面上获取测量值，菲涅耳场测量（Fresnel field，FrF）相比于远场测量，可以通过不同的策略获得更多的信息，例如，在不同传播距离获取多幅强度图案，从而降低过采样条件和（或）减少图像平面上的支撑集上的大量先验知识。
相位恢复的空间分辨率受到两个因素的限制：传播算子的低通滤波和传感器像素的大小[23-24]。对于传播算子的低通滤波，在强度观测中丢失了高频空间信息，可以将其视为下采样的真实目标，超分辨率成像允许补偿这种次抽样效应。而克服像素大小限制的一种直接方法是使用一系列横向移位的全息图[25-27]或散斑模式的亚像素扫描[28]。然而，运用传统的光学成像系统来解决空间分辨率低下依然是一个巨大的挑战。
基于传统相位恢复受空间分辨率和图像先验知识的双重限制，本文提出基于高速相位调制的菲涅耳场编码衍射图案实时获取成像方法，采用纯相位型硅基液晶（phase-only liquid crystal on silicon，PLCoS）或电可调透镜（electronically tunable lens, ETL）两种纯相位型空间调制器实现光场相位信息的高速动态调制，包括ETL的可变距离的快速聚焦或PLCoS透镜的灵活动态相位调制两种成像系统。初始目标经过ETL或PLCoS调制，调制后的光波通过自由空间传播到记录的平面，被CCD相机实时获取多幅编码衍射图案（coded diffraction patterns, CDPs）；将记录的CDPs利用WF算法重建光场的复振幅。本文提出的ETL成像系统可以有效地避免离散空间光调制器（spatial light modulator，SLM）栅格化结构、难以对准及调制速度慢等劣势。数值实验验证了本文方法的有效性和鲁棒性，可用于高分辨率场景的高速记录，具有较大的应用潜力。
1. 相位恢复算法基本原理
相位恢复旨在从测量振幅
$ {\boldsymbol{b}} $ 中恢复相位$ {\boldsymbol{x}} $ [1]，在数学上可表述为求解如下非线性方程：$$ \begin{gathered} {\text{find }}{\boldsymbol{x}}{\text{ }},{\text{ }}{\boldsymbol{x}} \in {\mathbb{C}^n} \hfill \\ {\text{s}}{\text{.t}}{\text{. }}\left| {{\boldsymbol{Ax}}} \right| = {\boldsymbol{b}}{\text{ }},{\boldsymbol{A}} \in {\mathbb{C}^{m \times n}}{\text{ }},{\boldsymbol{b}} \in {\mathbb{R}^m} \hfill \\ \end{gathered} $$ (1) 式中，测量矩阵
$ {\boldsymbol{A}} $ 为系统的正向算子，$ m $ 为测量次数，$ n $ 为信号长度，$ \left| \cdot \right| $ 算子表示取模运算。式（1）的振幅约束可以转换为求解式（2）的二次约束：
$$ {y_i} = {| {{\boldsymbol{a}}_i^{\rm{H}}{\boldsymbol{x}}} |^2},{\text{ }}i = 1,2, \cdots ,m $$ (2) 式中：
$ {y_i} $ 为测量的强度值；${{\boldsymbol{a}}_i}$ 为调制函数向量，与成像系统物理参数相关；上标$ {\rm H} $ 为共轭转置。采用最小二乘准则，将式（2）的问题转化为基于强度的经验损失函数优化问题，数学表达式如下：
$$ \min f\left( {\boldsymbol{z}} \right): = \frac{1}{{2m}}{\sum\limits_{i = 1}^m {( {{y_i} - {{| {{\boldsymbol{a}}_i^{\rm{H}}{\boldsymbol{z}}} |}^2}} )} ^2} $$ (3) 式中，
${\boldsymbol{z}}$ 相当于式（2）中的${\boldsymbol{x}}$ 。WF算法是使用迭代优化的方式求解式（3）的最小化问题[4]，该方法主要由两个部分组成：首先，通过谱方法来获取较为精确的初始化估计值；然后，用一种类似于梯度下降算法的更新规则来迭代估计值。WF算法的流程如下。
1）WF算法的输入：观测值
$ {\boldsymbol{y}}{\rm{ = (}}{y_1},{y_2},\cdots,{y_m}{{\rm{)}}^{\rm{T}}} $ ，观测向量${{\boldsymbol{a}}_i} \in {\mathbb{C}^n}$ ，步长为$ \;{\mu _t} $ ，迭代次数设置为$ T $ 。初始化常数$ \lambda $ ，其公式为：$$ {\lambda ^2} = n\frac{{\displaystyle\sum\limits_{i = 1} {{y_i}} }}{{\displaystyle\sum\limits_{i = 1} {{{\left\| {{{\boldsymbol{a}}_i}} \right\|}^2}} }} $$ (4) 式中，
$ n $ 为信号长度。2）通过求解矩阵
$ {\boldsymbol{Y}} $ 的最大特征值对应的特征向量$ {\tilde {\boldsymbol{x}}_0} $ ，使得$ {\tilde {\boldsymbol{x}}_0} $ 满足$ \left\| {{{\tilde {\boldsymbol{x}}}_0}} \right\| = \lambda $ ，所得到的$ {\tilde {\boldsymbol{x}}_0} $ 为估计初始值。其中，矩阵$ {\boldsymbol{Y}} $ 的表达式如下：$$ {\boldsymbol{Y}} = \frac{1}{m}\sum\limits_{i = 1}^m {{y_i}{{\boldsymbol{a}}_i}} {\boldsymbol{a}}_i^{\rm{H}} $$ (5) 式中，
$ m $ 为测量次数。3）最后从谱初估计的初始值
$ {\tilde {\boldsymbol{x}}_0} $ 出发，通过梯度更新的方法获得确切的解$ {\tilde {\boldsymbol{x}}_{t + 1}} $ ,迭代次数$ t = 1,2, \cdots ,T $ ，迭代更新如式（6）所示：$$ {\tilde {\boldsymbol x}_{t + 1}} = {\tilde {\boldsymbol x}_t} - \frac{{{\mu _t}}}{{\left\| {{{\tilde {\boldsymbol x}}_0}} \right\|}}\left( {\frac{1}{m}\sum\limits_{i = 1}^m {{{( {{y_i} - {{| {{\boldsymbol{a}}_i^{\rm{H}}{{\tilde {\boldsymbol{x}}}_t}} |}^2}} )}^2}( {{\boldsymbol{a}}_i^{\rm{H}}{{\boldsymbol{a}}_i}} ){{\tilde {\boldsymbol x}}_t}} } \right) $$ (6) 对式（6）进行不断迭代得到最终的重建结果。
2. 基于高速相位调制的菲涅耳场编码衍射图案实时获取方法
与SIPR[5-8]和DIPR方法[5]相比，MIPR方法[9]通过改变光学成像系统中的物理结构获得不同的编码衍射图案（CDPs），无需先验约束，通过利用不同的扫描策略（例如，重叠照明、多波长扫描、多角度照明、针孔扫描和多距离测量等方法），获得最佳收敛和高精度重建。
但是，上述方法在获取不同CDPs的过程中需要不断改变成像系统的物理结构，不仅缺乏应用灵活性，而且增加了相应的工作量。因此，本文提出基于高速相位调制的菲涅耳场编码衍射图案实时获取方法，其中的成像系统在获取多幅强度测量图案时，采用纯相位空间调制和相位的动态调制，使得成像结构简单且记录过程简便，大大减轻相应工作量。
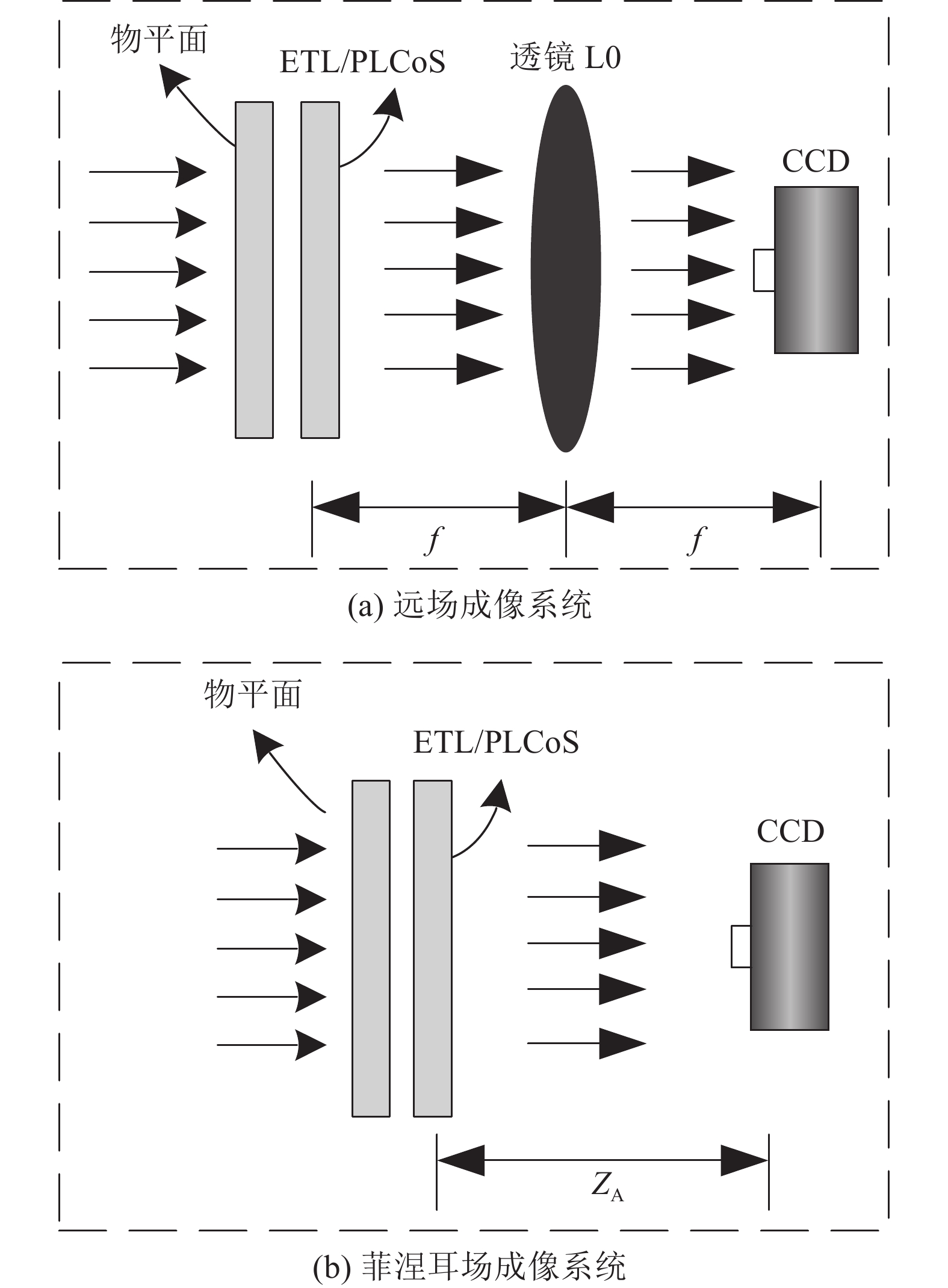
相位恢复的成像系统如图1所示。
图 1 远场和菲涅耳场相位恢复的成像系统Fig. 1 Imaging system for farfield and Fresnel field phase retrieval
下载:
全尺寸图片
图1（a）为傅里叶成像系统（等价于远场FF成像系统），其中，ETL/PLCoS、CCD分别放置在透镜L0的前焦面和后焦面，焦距为
$ f $ 。菲涅耳场相位恢复记录强度的成像光学系统设置如图1（b）所示，物光场经过ETL或PLCoS随机调制，再通过自由空间传播到$ {Z_{A}} $ 处的记录平面（其中$ {Z_{A}} $ 为传播距离），最终由光电探测器CCD记录CDPs。傅里叶成像系统中，相位恢复的目的是从CCD上记录的噪声干扰测量的无相位非线性测量信号
${{\boldsymbol{Y}}}$ 中重建2维复光场${\boldsymbol{X}}$ ，具体表示为：$$ {\boldsymbol{Y}} = {\left| {F({\boldsymbol{X}})} \right|^2} + e $$ (7) 式中：
$e$ 为成像系统的随机噪声；$F( \cdot ):{\mathbb{C}^{{N_1} \times {N_2}}} \to {\mathbb{C}^{{M_1} \times {M_2}}}$ 为线性算符，在傅里叶光学成像系统中线性算符$ F( \cdot ) $ 为经过$L$ 个掩膜调制的编码衍射图案成像模型，可表示为：$$ F({\boldsymbol{X}}) = {\left( {FT({M^1} \odot {\boldsymbol{X}}),FT({M^2} \odot {\boldsymbol{X}}), \cdots ,FT({M^L} \odot {\boldsymbol{X}})} \right)^{\rm{T}}} $$ (8) 式中：
$ {\boldsymbol{X}} $ 为物体的复光场；${M^l}$ 为第$ l $ 个调制掩模，$l = 1,2, \cdots ,L$ ；$ \odot $ 表示Hadamard积；$ FT $ 表示2维傅里叶变换。线性算符的伴随算符（adjoint operator）为：
$$ {F^*}({\boldsymbol{Z}}) = \sum\limits_{l = 1}^L {( {\overline {{M^l}} \odot F{T^*}({{\boldsymbol{Z}}_l})} )} $$ (9) 式中：
$ \overline {{M^l}} $ 为掩模${M^l}$ 的共轭；$ F{T^*} $ 表示$ FT $ 的逆算符，即2维傅里叶逆变换。在菲涅耳场成像系统中，物光场经过ETL/PLCoS随机调制，再通过自由空间传播到记录平面，其编码衍射图案成像模型为：
$$ \begin{aligned}[b] FRT({\boldsymbol{X}}) =& ( FrT({M^1} \odot {\boldsymbol{X}}),FrT({M^2} \odot {\boldsymbol{X}}), \cdots ,\\& FrT({M^L} \odot {\boldsymbol{X}}) )^{\rm{T}} \end{aligned} $$ (10) 式中：
$ FRT\left( \cdot \right) $ 表示菲涅耳场成像模型对应的线性映射算符；$ FrT( \cdot ) $ 表示2维菲涅耳变换，其对应于菲涅耳场成像中主要变换。$ FRT\left( \cdot \right) $ 的伴随算符为：$$ FR{T^*}({\boldsymbol{Z}}) = \sum\limits_{l = 1}^L {( {\overline {{M^l}} \odot Fr{T^*}({{\boldsymbol{Z}}_l})} )} $$ (11) 式中，
$ Fr{T^*} $ 表示$ FrT( \cdot ) $ 的逆算符，即2维菲涅耳里叶逆变换。为实现高精度相位恢复，需要构造具有高匹配度的线性算符及其伴随算符，对于式（8）～（11）而言，要求：
$$ {M^l} \odot \overline {{M^l}} = {\boldsymbol{D}},{\text{ }}l = 1,2, \cdots ,L $$ (12) 式中，
$ {\boldsymbol{D}} $ 为全1矩阵，即矩阵所有元素为1。为保证满足式（12），最常见的选择是设计随机相位掩膜调制。因此，本文提出采用纯相位型空间光调制器实现相位的动态调制，例如，纯相位型硅基液晶（PLCoS）、电可调透镜（ETL）等光学元件动态调制，获取多幅不同的编码衍射图案用于相位恢复。PLCoS的调制函数表示为：
$$ {P^l}\left( {x,y} \right) = \exp ( {{\rm i} \times 2{\text{π}} \times {p^l}( {x,y} )} ) $$ (13) 式中，
$ {p^l}\left( {x,y} \right) $ 为相位函数，其值为[0,1]之间的均匀分布。ETL的调制函数可表示为：
$$ {P^l}\left( {x,y} \right) = \exp \left[ { - \frac{{{\rm i}k}}{{2f_{{\rm{ETL}}}^l}}( {{x^2} + {y^2}} )} \right] $$ (14) 式中，
$f_{{\rm{ETL}}}^l$ 为ETL的可调焦距，波数$k = 2{\text{π/}}\lambda$ 。本文提出基于高速相位调制的菲涅耳场编码衍射图案实时获取方法，运用WF算法在PLCoS/ETL纯相位型空间光调制器获取的菲涅尔场多幅编码衍射图案下重建复光场。其菲涅耳场相位恢复原理如图2所示。
图 2 菲涅耳场相位恢复原理图Fig. 2 Schematic diagram of Fresnel field phase retrieval下载:
全尺寸图片
由图2可知本文提出的方法包括4个主要模块：1）初始化模块，初始化位于物平面的复振幅，其由原始振幅和原始相位组成。2）调制函数生成模块。纯相位型空间光调制器的调制函数由振幅和相位两部分组成，由于是纯相位调制，振幅为单位振幅，而相位分布有两种：一种是ETL产生的透镜相位分布（ETL），另一种是PLCoS对应的是随机相位调制（random phase modulation，RPM）的分布。3）记录CDPs模块。经过ETL和PLCoS的随机相位调制，沿着光轴传播方向
$ {Z_A} $ 处的探测平面记录多幅编码衍射图案（CDPs）。4）重建模块。利用WF算法从多幅编码衍射图案中分别恢复的复光场。3. 仿真实验
为了验证本文提出的基于高速相位调制的菲涅耳场编码衍射图案实时获取方法的有效性和鲁棒性，设计远场（FF）和菲涅耳场（FrF）成像系统对比，实现5组仿真对比实验。
3.1 单次重建实验
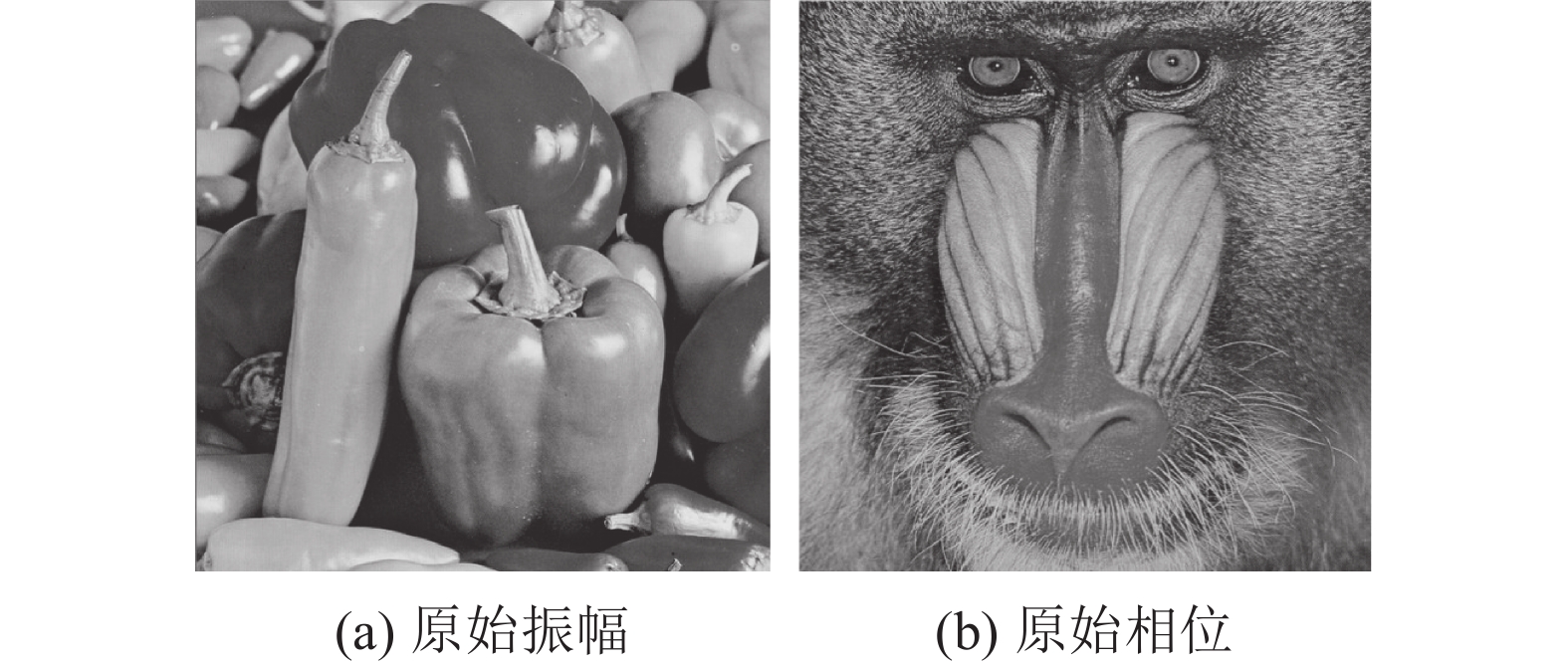
验证在菲涅耳场（FrF）与远场（FF）成像条件下对比使用ETL和PLCoS随机相位调制获取不同CDPs重建复光场的可行性。选取尺寸为128×128像素的标准peppers和baboon图像分别作为复光场的振幅和相位，其中，peppers图像灰度值归一化到
$[0,1]$ 区间作为原始振幅，baboon图像灰度值归一化到$ ( - {\text{π}},{\text{π}}) $ 作为原始相位分布，如图3所示。
图 3 原始对象的振幅和相位Fig. 3 Amplitude and phase of the original object下载:
全尺寸图片
用于生成CDPs的ETL/RPM的掩膜数量
$ L $ 为15。菲涅耳场成像系统的传播距离$ {Z_A} $ 是10 mm，波长为0.532 μm，原始测试对象的像素大小为5 μm×5 μm，ETL的可调焦距范围是0.1～14.5 mm，其中步长为0.6 mm。实验是在无噪声条件下分别通过远场和菲涅耳场成像系统生成不同的CDPs，并利用WF算法进行重建，设置WF算法的梯度下降的迭代次数为900。实验使用了2种不同的纯相位型空间调制器（ETL/PLCoS），对应2种不同的相位调制方式（ETL/RPM），分别在远场（FF）和菲涅耳场（FrF）下共4种不同成像系统进行单次重建实验，重建效果图如图4所示。图4中，4列分别对应FF_ETL（远场+ETL）、FF_RPM（远场+ RPM），以及本文提出的FrF_ETL（菲涅耳场+ETL）和FrF_RPM（菲涅耳场+RPM）4种不同系统单次重建实验结果，实验得到的快速随机调制的振幅、相位和强度测量都各有15个结果，仅各给出其中1个结果作为实例。当重建复振幅的信噪比（signal-to-noise ratio，SNR）约为40 dB，可以认为重建成功，4个不同成像系统的重建复振幅的SNR分别为357.27、292.90、315.22和280.02 dB。从图4可以看出，无论是菲涅耳场（FrF）成像还是远场（FF）成像，采用PLCoS/ETL随机调制记录的多幅编码衍射图案可以实现光场复振幅的有效重建，说明在菲涅耳场条件下采用PLCoS/ETL同样可以实现菲涅耳场相位信息的有效获取。
图 4 单次重建实验对比Fig. 4 Comparison of single reconstruction experiments下载:
全尺寸图片
3.2 不同迭代次数下的相位重建实验
本实验采取不同掩膜数量，分别在FF_ETL、FF_RPM， FrF_ETL和FrF_RPM 4种不同成像系统下测试相位恢复性能与WF算法的梯度下降迭代次数之间的关系。测试对象是由标准Lena和baboon图像分别作为振幅图像和相位图像合成的，归一化方式与第3.1节相同，其像素大小与第3.1节保持一致。分别在远场和菲涅耳场中通过ETL和RPM随机相位调制生成多幅编码衍射图案，其中，不同成像系统对应不同的相位掩膜生成方式，均在不同数量掩膜下进行单次重建实验，将梯度下降的迭代次数分别设置为150、300、450、600、750、900、1 000，利用SNR评估重建复振幅的质量，判断成功重建的标准是在无噪声下重建复振幅的SNR约为40 dB。重建复振幅的SNR随着迭代次数的变化曲线如图5所示。从图5中可以看出，总体而言，随着迭代次数的增加，从4种成像系统记录的CDPs中重建复振幅的SNR也逐渐增加。
图 5 SNR随着迭代次数变化的曲线Fig. 5 Curves of SNR with iteration times下载:
全尺寸图片
由图5还可知：当WF算法梯度下降的迭代次数达到900次时，4种成像系统在不同掩膜数量下的重建性能基本保持稳定，所以本文后续实验都选取迭代次数为900。对于不同的成像系统，成功重建所需的最少掩膜数量不同。在远场成像条件下，采用ETL（即FF_ETL）相位掩膜调制需要的最少编码衍射图案数目（即掩膜数量）
$ L = 7 $ （$ L \le 6 $ 时重建失败），而RPM（即FF_RPM）需要的最少掩膜数量$ L = 8 $ （$ L \le 7 $ 时重建失败）。在菲涅耳场成像条件下，采用ETL（即FrF_ETL）相位掩膜调制需要的最少掩膜数量$ L = 11 $ ，此时重建复振幅的SNR约为40 dB，可以认为重建成功，而RPM（即FrF_RPM）需要的最少掩膜数量$ L = 7 $ （$ L \le 6 $ 时重建失败）。实验结果表明，在远场成像和菲涅耳场成像条件下使用ETL或RPM随机调制可以实现复光场的有效调制与高质量重建。3.3 不同数量的掩膜下的重建实验
本实验分别在FF_ETL、FF_RPM、FrF_ETL和FrF_RPM 4种不同成像系统下测试相位恢复性能与掩膜数量之间的关系。测试对象及其生成方式、随机相位调制方式及像素大小与第3.2节保持一致。根据第3.2节结果，设置WF算法梯度下降的迭代次数为900。每组参数条件下的实验独立运行40次，计算重建复振幅的平均重建信噪比（average signal-to-noise ratio，ASNR），并计算重建成功率。远场（FF）或菲涅耳场（FrF）成像系统的ASNR和重建成功率随着腌膜数量变化的对比结果如图6所示。从图6（a）中可以看出，从总体趋势而言，随着用于生成CDPs的掩膜数量的增加，4种成像系统记录的重建复振幅的ASNR也逐渐增加。当掩膜数量
$ L = 14 $ 时，这4种成像系统的性能基本趋于一致。在$ L = 7 $ 时：FF_ETL的ASNR数值较高，结合图6（b）可知此时其重建成功率接近60%；而此时FF_RPM的ASNR数值较低，结合图6（b）可知，此时其重建成功率接近20%，在$ L = 8 $ 时，其重建成功率提升到接近80%。在$ L = 7 $ 时，FrF_RPM的ASNR数值较高，结合图6（b）可知，此时其重建成功率接近40%，而在$ L = 8 $ 时其重建成功率提升到接近90%。在L = 6～11时，FrF_ETL的ASNR数值增长较缓慢，其性能最差。总的来说，图6（b）的重建成功率曲线与图6（a）曲线的走势规律基本一致。
图 6 ASNR和重建成功率随着腌膜数量变化的曲线Fig. 6 Curves of ASNR and the success rates of reconstruction with the change of the number of salted films下载:
全尺寸图片
3.4 不同噪声水平下的重建实验
本实验分别在FF_ETL、FF_RPM、FrF_ETL和FrF_RPM 4种不同成像系统下测试平均重建信噪比与测量噪声之间的关系。测试对象及其生成方式、随机相位调制方式及像素大小与第3.2节保持一致。随机相位掩膜为ETL产生的变焦透镜相位掩膜和PLCoS产生的RPM，WF算法的梯度下降迭代次数固定为900。使用WF算法重建时给测量值
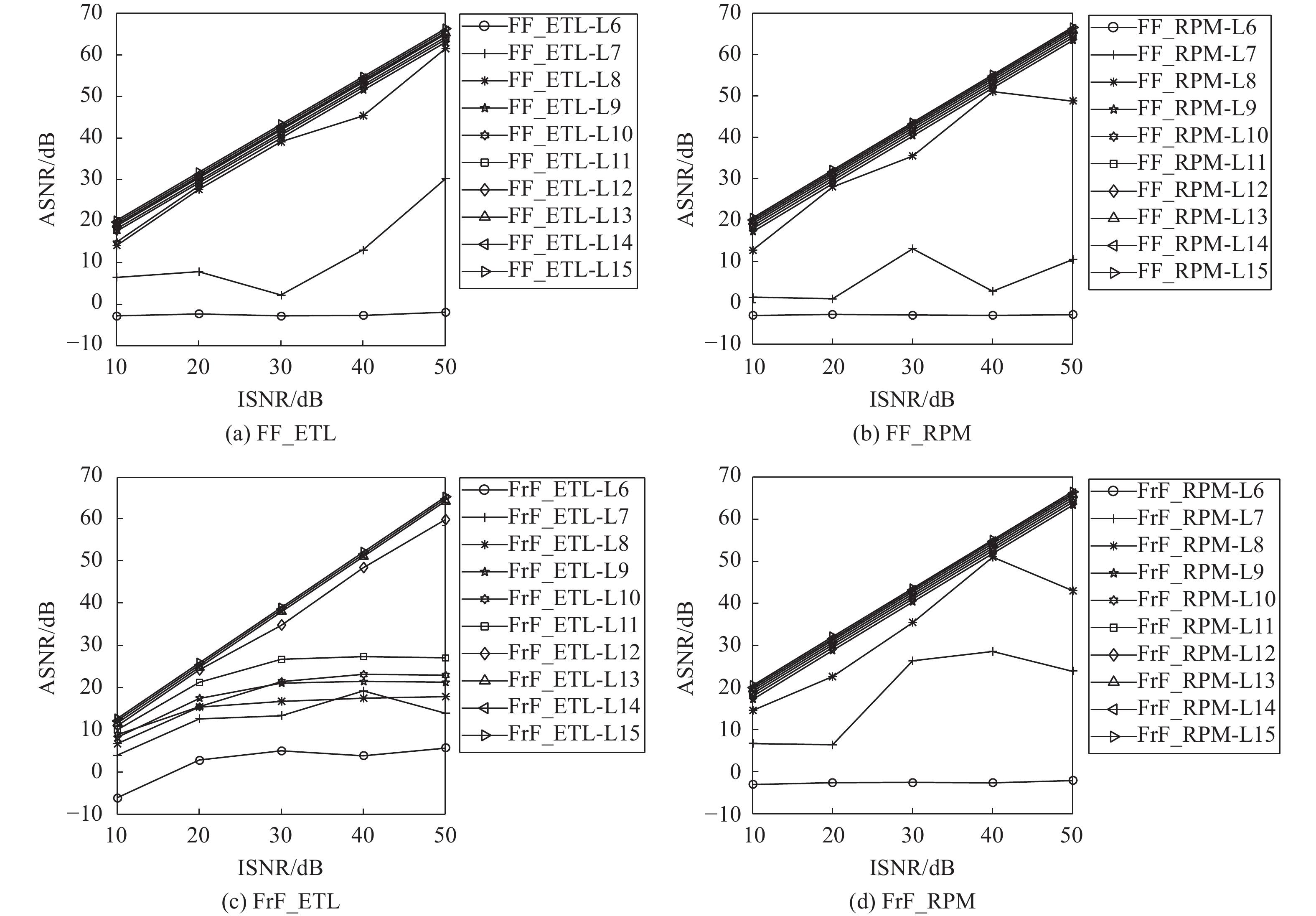
${\boldsymbol{Y}}$ 加入不同SNR的噪声，噪声的加入通过MATLAB软件自带的awgn函数来实现；调整加性高斯白噪声方差使得测量值的输入信噪比（input signal-to-noise ratio，ISNR）在10～50 dB之间，步长为5 dB，其中，${\text{ISNR}} = {\text{SNR}}\left( {\left| {F \left( {\boldsymbol X} \right),{\boldsymbol{Y}}} \right|} \right)$ ，ISNR值反映成像系统中的测量噪声水平；由于随机噪声的不确定性，不同噪声水平实验在相同参数下独立运行50次，并计算重建复振幅的ASNR；在不同的成像系统和不同数量的掩膜下得到ASNR随着ISNR（噪声水平）变化的曲线如图7所示。
图 7 ASNR随着噪声水平变化的曲线Fig. 7 Curves of ASNR changing with different noise levels下载:
全尺寸图片
从图7中可以看出：总体而言，随着测量值Y的ISNR值增大，即测量噪声方差减小，ASNR逐渐增加。随掩膜数量的增加，不同成像系统的ASNR的差异较大，这反映了不同成像系统的抗噪声性能的差异。对于远场系统，无论是ETL还是RPM随机调制，通过WF算法都可以实现复光场的精确重建，当掩膜数量
$ L \ge 8 $ 时，FF_ETL和FF_RPM的ASNR近似与ISNR（噪声水平）呈线性增长。掩膜数量的增加对重建ASNR有一定的提高，但提高不明显。相比远场系统，菲涅耳场成像系统中无论是ETL还是RPM随机调制，其复光场的重建ASNR值要略差，也就是说菲涅耳场系统的抗噪性较差。在菲涅耳场的两种相位调制方式中，对于FrF_ETL，只有当掩膜数目$ L \ge 12 $ 时ASNR与ISNR（噪声水平）呈现出与远场成像类似的线性关系；对于FrF_RPM，当$ L \ge 9 $ 时ASNR与ISNR（噪声水平）呈现出与远场成像类似的线性关系；因此FrF_ETL抗噪声性能最差。其背后深层原因是菲涅耳场系统中ETL的可调控自由度要远远小于利用PLCoS调制的RPM的可调控自由度。ETL只有1个自由度，即可变焦距
$ f_{{\text{ETL}}}^l $ ，通过改变焦距，来改变ETL的相位分布；而PLCoS的自由度为M×N×L。但是，随着掩膜数量L的增加，ETL透镜测量的多样性也可以达到PLCoS相位调制类似的效果。需要强调的是，电可调透镜ETL利用其高速变焦距功能，可用于高速获取多次曝光的编码衍射图案，则适用于快速和大尺度场景的相位恢复，并且具有快速、高分辨率、大景深（depth-of-field，DOF）、高灵敏度和低成本成像等优点。此外，PLCoS是离散栅格结构，其调制速度远远低于ETL。3.5 不同算法下的重建实验
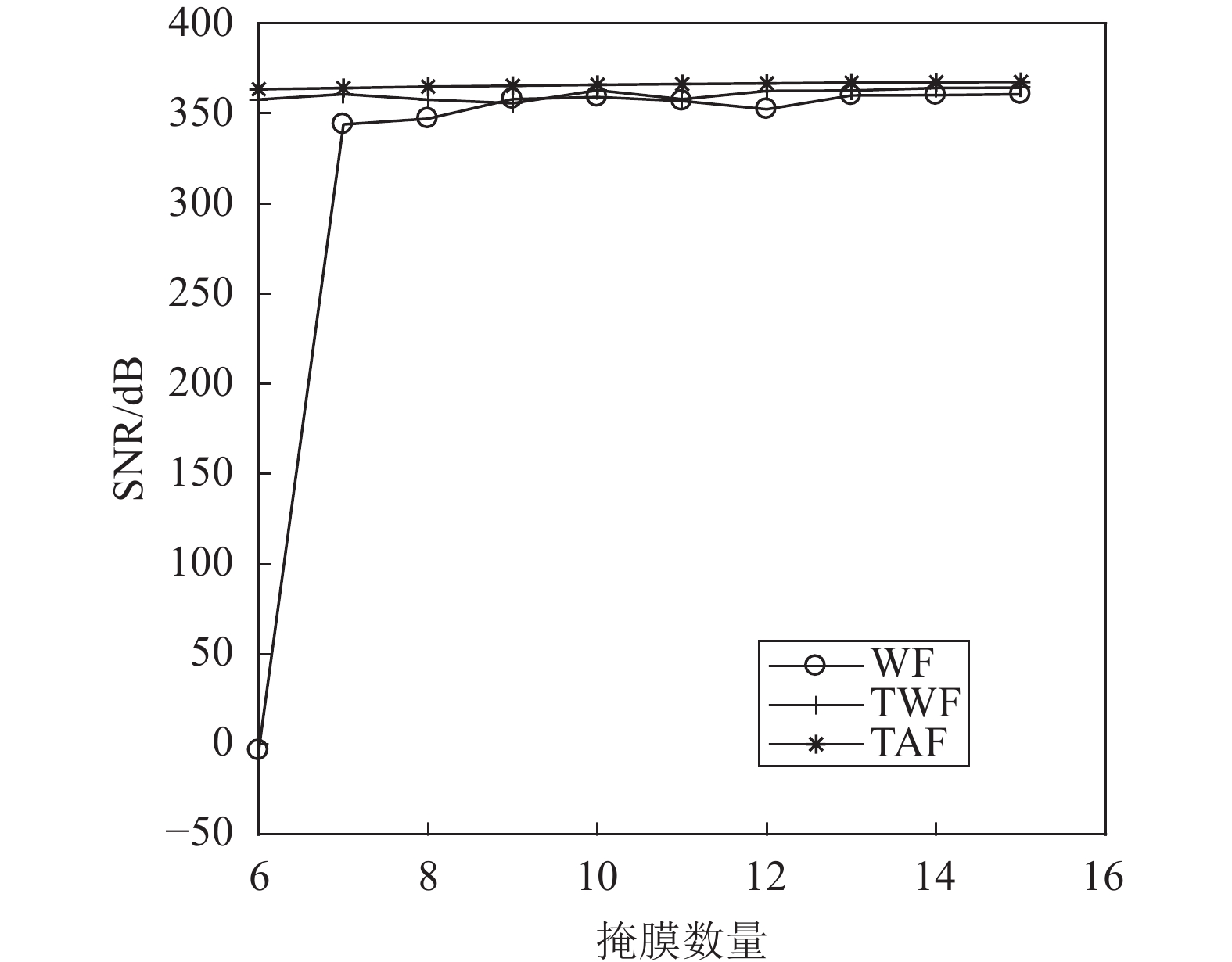
测试在FF_ETL和FF_RPM成像系统下使用WF、TWF、TAF不同算法的重建质量与掩膜数量之间的关系。测试对象以及其生成方式、随机相位调制方式及像素大小与第3.2节保持一致，WF算法梯度下降的迭代次数为900。针对不同算法和不同数量的掩膜进行单次重建实验，利用SNR评估重建复振幅的质量，不同算法随着掩膜数量变化如图8所示。
图 8 不同算法随着掩膜数量变化的曲线Fig. 8 Curves of changes of different algorithms with the number of masks下载:
全尺寸图片
从图8可以看出，随着掩膜数量的增加，3种算法从远场成像系统记录的CDPs中重建复振幅的SNR也逐渐增加。当掩膜数量为大致为7时，3种算法的重建性能基本保持稳定，所以，WF、TWF、TAF这3种算法在FF_ETL和FF_RPM成像系统下即使掩膜数量发生变化，也能够较好地重建振幅和相位。
4. 结 论
本文提出一种基于高速相位调制的菲涅耳场编码衍射图案实时获取方法，将多幅编码衍射图案运用WF算法可实现相位的最佳收敛和高精度重建，无需额外的先验知识。其基本思想是采用纯相位型空间调制器进行相位的动态调制，其中，包括ETL的可变距离的快速聚焦或纯相位PLCoS透镜的灵活动态相位调制，ETL成像系统可以有效地避免离散空间光调制器（spatial light modulator，SLM）栅格化结构、难以对准和调制速度慢等劣势；并且不需要透镜等装置，可以直接传播到记录平面；在采集阶段，使用一系列横向移位的全息图克服像素大小的限制，能够得到多幅不一样的编码衍射图案；在复振幅重建阶段，无需额外的先验知识，使用WF算法能够较好地重建振幅和相位信息。对本文方法进行单次重建实验，由实验结果可以看出，菲涅耳场成像采用PLCoS或ETL随机调制记录多幅编码衍射图案，可以实现光场复振幅的有效重建。本文通过对远场（FF）和菲涅耳场（FrF）在不同迭代次数、不同掩膜数量、不同噪声水平及不同算法下分别进行对比实验，一系列的测试结果表明本文方法的有效性和鲁棒性。相比于传统获取多强度的成像系统，本文所提出的成像系统更为紧凑和简单，避免了反复对齐与校准的工作量，具有重要的应用潜力。本文方法可用于实时采集多幅编码衍射图样，适用于快速和大规模相位恢复场景，并且具有高分辨率和可扩展性等优势。基于现有的工作，所提成像系统中PLCoS与CCD之间的距离等参数会直接影响着测试系统的性能，下一步研究中要对实验参数进行更加精确的测量，以保证获得更准确的结果。
-
图 1 远场和菲涅耳场相位恢复的成像系统
Fig. 1 Imaging system for farfield and Fresnel field phase retrieval
下载:
全尺寸图片
图 2 菲涅耳场相位恢复原理图
Fig. 2 Schematic diagram of Fresnel field phase retrieval
下载:
全尺寸图片
图 3 原始对象的振幅和相位
Fig. 3 Amplitude and phase of the original object
下载:
全尺寸图片
图 4 单次重建实验对比
Fig. 4 Comparison of single reconstruction experiments
下载:
全尺寸图片
图 5 SNR随着迭代次数变化的曲线
Fig. 5 Curves of SNR with iteration times
下载:
全尺寸图片
图 6 ASNR和重建成功率随着腌膜数量变化的曲线
Fig. 6 Curves of ASNR and the success rates of reconstruction with the change of the number of salted films
下载:
全尺寸图片
图 7 ASNR随着噪声水平变化的曲线
Fig. 7 Curves of ASNR changing with different noise levels
下载:
全尺寸图片
图 8 不同算法随着掩膜数量变化的曲线
Fig. 8 Curves of changes of different algorithms with the number of masks
下载:
全尺寸图片
-
[1] Shechtman Y,Eldar Y C,Cohen O,et al.Phase retrieval with application to optical imaging:A contemporary overview[J].IEEE Signal Processing Magazine,2015,32(3):87–109. doi: 10.1109/MSP.2014.2352673 [2] Gerchberg R.A practical algorithm for the determination of phase from image and diffraction plane pictures[J].Optik,1972,35:237–246. [3] Candès E J,Eldar Y C,Strohmer T,et al.Phase retrieval via matrix completion[J].SIAM Review,2015,57(2):225–251. doi: 10.1137/151005099 [4] Candès E J,Li Xiaodong,Soltanolkotabi M.Phase retrieval via Wirtinger flow:Theory and algorithms[J].IEEE Transactions on Information Theory,2015,61(4):1985–2007. doi: 10.1109/TIT.2015.2399924 [5] Zhang Cheng,Wang Meiqin,Chen Qianwen,et al.Two-step phase retrieval algorithm using single-intensity measurement[J].International Journal of Optics,2018,2018:8643819. doi: 10.1155/2018/8643819 [6] Fienup J R.Phase retrieval algorithms:A comparison[J].Applied Optics,1982,21(15):2758. doi: 10.1364/ao.21.002758 [7] Fienup J R.Phase retrieval algorithms:A personal tour[J].Applied Optics,2013,52(1):45–56. doi: 10.1364/AO.52.000045 [8] Cai T T,Li Xiaodong,Ma Zongming.Optimal rates of convergence for noisy sparse phase retrieval via thresholded Wirtinger flow[EB/OL].[2021–04–02].https://arxiv.org/abs/1506.03382. [9] Guo Cheng,Shen Cheng,Li Qiang,et al.A fast-converging iterative method based on weighted feedback for multi-distance phase retrieval[J].Scientific Reports,2018,8:6436. doi: 10.1038/s41598-018-24666-8 [10] Wu J S,Weierstall U,Spence J C H,et al.Iterative phase retrieval without support[J].Optics Letters,2004,29(23):2737–2739. doi: 10.1364/ol.29.002737 [11] Chen Pengwen,Fannjiang A,Liu G R.Phase retrieval with one or two diffraction patterns by alternating projections with the null initialization[J].Journal of Fourier Analysis and Applications,2018,24(3):719–758. doi: 10.1007/s00041-017-9536-8 [12] Wang Gang,Giannakis G B,Eldar Y C.Solving systems of random quadratic equations via truncated amplitude flow[J].IEEE Transactions on Information Theory,2018,64(2):773–794. doi: 10.1109/TIT.2017.2756858 [13] Dean B H,Bowers C W.Diversity selection for phase-diverse phase retrieval[J].Journal of the Optical Society of America A,2003,20(8):1490. doi: 10.1364/josaa.20.001490 [14] Guo Cheng,Zhao Yixuan,Tan Jiubin,et al.Multi-distance phase retrieval with a weighted shrink-wrap constraint[J].Optics and Lasers in Engineering,2019,113:1–5. doi: 10.1016/j.optlaseng.2018.09.017 [15] Liu Zhengjun,Guo Cheng,Tan Jiubin.Lensfree computational imaging based on multi-distance phase retrieval[J].Infrared and Laser Engineering,2018,47(10):1002002. doi: 10.3788/irla201847.1002002 [16] Jaganathan K,Eldar Y,Hassibi B.Phase retrieval with masks using convex optimization[C]//Proceedings of the 2015 IEEE International Symposium on Information Theory.Hong Kong:IEEE,2015:1655–1659. [17] Liu Zhengjun,Geng Yong,Tan Jiubin.Computational imaging based on multi-rotations measurement of cylinder lens[J].Infrared and Laser Engineering,2019,48(6):603016. doi: 10.3788/irla201948.0603016 [18] Hu Zhukuan,Tan Cuimei,Song Zhenzhen,et al.A coherent diffraction imaging by using an iterative phase retrieval with multiple patterns at several directions[J].Optical and Quantum Electronics,2019,52(1):1–10. doi: 10.1007/s11082-019-2149-5 [19] Guizar–Sicairos M,Fienup J R.Phase retrieval with transverse translation diversity:A nonlinear optimization approach[J].Optics Express,2008,16(10):7264–7278. doi: 10.1364/oe.16.007264 [20] Michalko A M,Fienup J R.Transverse translation diverse phase retrieval using soft-edged illumination[J].Optics Letters,2018,43(6):1331–1334. doi: 10.1364/OL.43.001331 [21] Michalko A M,Fienup J R.Verification of transverse translation diverse phase retrieval for concave optical metrology[J].Optics Letters,2018,43(19):4827–4830. doi: 10.1364/OL.43.004827 [22] Zhai Yulan,Guo Cheng,Zhang Feilong,et al.Adjustable frequency filtering and weighted feedback for iterative phase retrieval under noisy conditions[J].Optics and Lasers in Engineering,2020,124:105808. doi: 10.1016/j.optlaseng.2019.105808 [23] Katkovnik V,Shevkunov I,Petrov N V,et al.Computational super-resolution phase retrieval from multiple phase-coded diffraction patterns:Simulation study and experiments[J].Optica,2017,4(7):786. doi: 10.1364/optica.4.000786 [24] Katkovnik V Y,Egiazarian K.Sparse superresolution phase retrieval from phase-coded noisy intensity patterns[J].Optical Engineering,2017,56:094103. doi: 10.1117/1.OE.56.9.094103 [25] Bishara W,Sikora U,Mudanyali O,et al.Holographic pixel super-resolution in portable lensless on-chip microscopy using a fiber-optic array[J].Lab on a Chip,2011,11(7):1276–1279. doi: 10.1039/c0lc00684j [26] Guo Kaikai,Dong Siyuan,Nanda P,et al.Optimization of sampling pattern and the design of Fourier ptychographic illuminator[J].Optics Express,2015,23(5):6171–6180. doi: 10.1364/OE.23.006171https://pubmed.ncbi.nlm.nih.gov/25836839/ [27] Greenbaum A,Luo Wei,Khademhosseinieh B,et al.Increased space-bandwidth product in pixel super-resolved lensfree on-chip microscopy[J].Scientific Reports,2013,3:1717. doi: 10.1038/srep01717 [28] Almoro P,Pedrini G,Osten W.Aperture synthesis in phase retrieval using a volume-speckle field[J].Optics Letters,2007,32(7):733–735. doi: 10.1364/ol.32.000733
