Design and Experiment of Muck Removal Robot for Tunneling Boring Machine
-
摘要: 隧道底部积渣清理是TBM（tunneling boring machine）施工中钢拱架立拱前的必备环节，随着人们对支护质量、施工效率、安全性的要求越来越高，传统的人工清渣难以满足施工要求。基于此，提出一种机器人作业的清渣方法。首先，分析隧道底部积渣分布情况与环境结构特点，获得机器人设计要求，进行新型机器人机构设计；其次，基于Denavit–Hartenberg（D–H）参数法建立其连杆坐标系，进行正逆运动学计算，给出末端位姿矩阵的表达式和逆运动学最优解的选取算法，并进行工作空间计算和分析；然后，以单关节位置控制为例，进行积分分离PID控制器设计；最后，搭建了隧道底部积渣清理试验平台，并进行隧道底部积渣清理试验。结果表明：新型清渣机器人能够实现3 830 mm的作业深度和±45°的作业范围；与传统PID相比，积分分离PID将超调量降低18.7%，解决了位置误差累积引起的关节抖动问题，改善系统控制效果；该清渣机器人作业周期为53 s，可作为敞开式TBM施工过程隧道底部积渣清理的有效解决方案。Abstract: Muck removal at the bottom of tunnel is required before steel arch erection in tunneling boring machine (TBM) construction. With the increasing requirements for quality, efficiency and safety, the traditional manual muck removal is difficult to meet the construction requirements. A muck removal method for the robot was proposed. Firstly, the distribution of muck at the bottom of the tunnel and the characteristics of the environmental structure were analyzed, the design requirements of the robot were obtained, and the new robot structure was designed. Secondly, the link coordinate system was established based on the Denavit–Hartenberg (D–H) parameter method, the forward and inverse kinematics were calculated, the matrix of the end positional and the selection algorithm of the optimal solution of the inverse kinematics were presented, and the workspace was calculated and analyzed. The results showed that the robot could achieve a working depth of 3 830 mm and a working range of ± 45°. Then, taking the single joint position control as an example, the integral separation PID controller was designed. Compared with the traditional PID, the overshoot was reduced by 18.7%, and the problem of joint jitter caused by the accumulation of position error was solved. Finally, the test platform of the muck removal robot was built, and the muck removal experiment was conducted. The results showed that it took 53 seconds to clean muck, which could be used as an effective solution for muck removal at the bottom of the tunnel during open TBM construction.
-
Keywords:
- tunneling boring machine /
- muck removal robot /
- structural design /
- control /
- experiment
-
川藏铁路是国家“十四五”期间铁路规划重大建设项目，对引导产业布局、促进沿线国土开发、巩固国防安全具有重要战略意义。如何高标准、高起点、高质量建设川藏铁路是当下全国社会各界普遍关注的热点和焦点问题[1]。杜闯东[2]、刘卓[3]等总结前期相关调查研究，结合川藏铁路建设总体要求、地质条件、环境特征和各类隧道掘进机（tunnel boring machine，TBM）特点，提出推广应用全断面TBM是科学高效建成川藏铁路的有效途径之一。
由于隧道路段具有破碎带多、地应力高（最高可达78 MPa）等地质特点[4-5]，在TBM施工过程中，岩爆、顶部坍塌掉块等现象频发，易导致石渣、岩块大量堆积在钢拱架安装机附近，因此，隧道底部积渣清理成为TBM施工过程的必备环节。目前，石渣主要由人工采用铁锹和编织袋将积渣装袋[6]，然后由运渣车或放置在皮带机上随皮带机运输出去。但由于川藏线路高寒（最低气温–30 ℃）、缺氧（全线平均海拔3 800 m）、高地热及局部地段经过含煤地层（检测出CH4、SO2、H2S、CO等有害气体），极易导致人员伤亡。因此，传统的人工清渣已无法满足施工要求，实现机械化换人、自动化减人、智能化解放人势在必行[7]。
德国Herrenknecht公司采用一种小型装载机进行清渣作业，但该设备对工作空间和操作人员技能要求较高，且采用装载机进行积渣转运时容易影响洞内交通；美国的Robbins设计了一种4自由度清渣机械臂，但运渣作业仍需人工进行；中铁十八局集团隧道工程有限公司设计的一种清渣系统[8]通过设计的小皮带机将石渣及废弃物输送至斗式提升机，斗式提升机将石渣转运至主机皮带机，随主机皮带机运出洞外，但设备所占空间较大，且需要人工将积渣堆积在小皮带机上，仅实现了运渣自动化。综上所述，隧道底部积渣清理总体尚未实现自动化。
针对上述问题，以提高TBM对不良地质的适应性和TBM隧道底部积渣清理自动化为目标，基于视觉和雷达，提出一种机器人清渣方案，并进行一种新型TBM清渣机器人机构设计和仿真；最后，搭建隧道底部积渣清理试验台，验证该方案的可行性，并将该技术成果应用于工程实践。
1. 清渣机器人机构设计
1.1 清渣机器人工况分析
根据清渣实际工况（图1），积渣主要散落在隧道底部±45°区域内[9]，体量特征沿隧道轴线方向随机分布，如图2所示。按照20 min的钢拱架拼装时间，清渣要在钢拱架拼装最后一环前完成，考虑20%的余量，清渣作业需在16 min内完成。
图 1 清渣实际工况Fig. 1 Actual working condition of muck removal
下载:
全尺寸图片
图 2 隧道清渣区域示意图Fig. 2 Schematic diagram of muck removal area in tunnel下载:
全尺寸图片
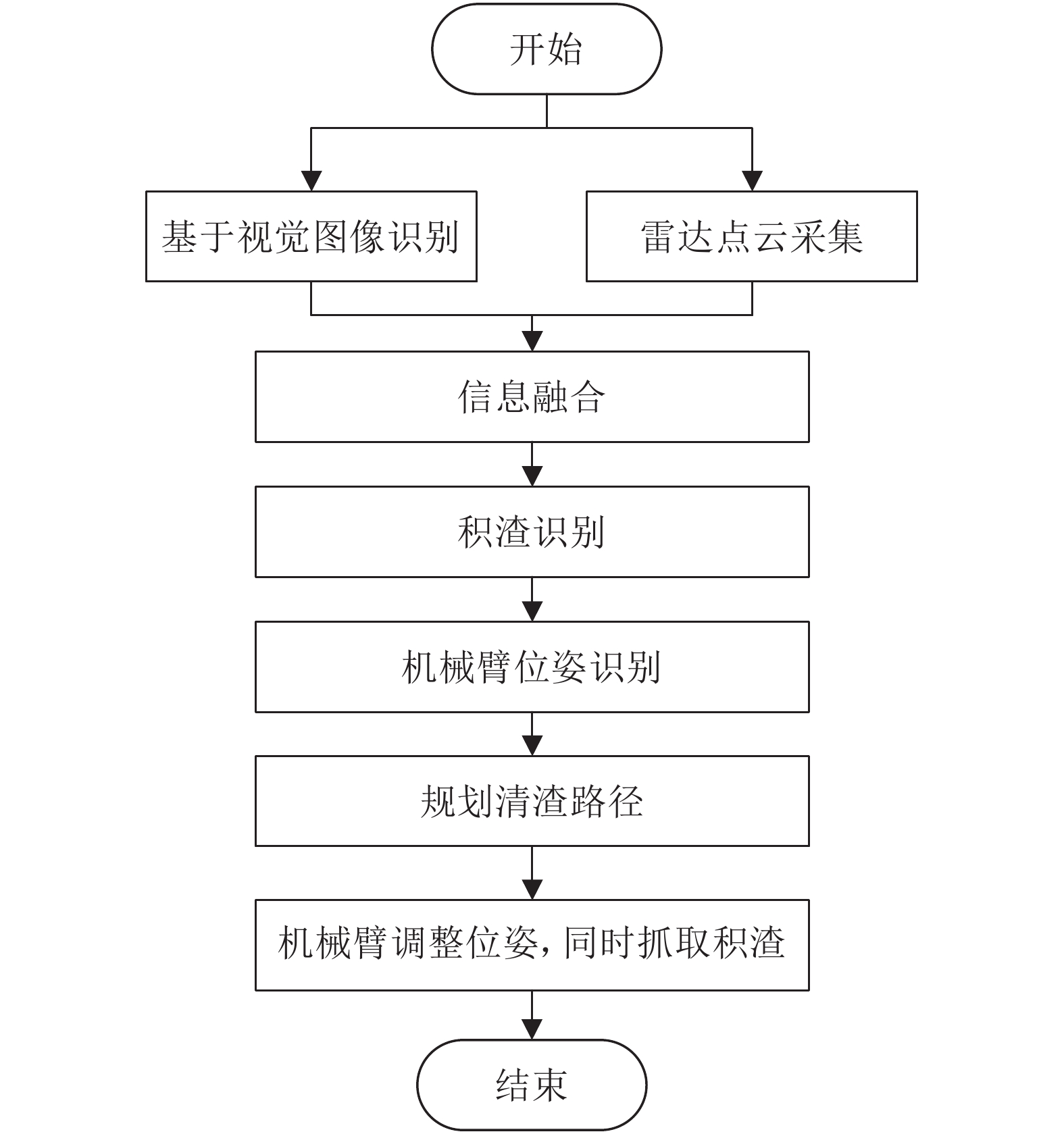
为实现清渣作业的机械化、自动化甚至是智能化，根据施工实际工况及隧道清渣区域范围，将摄像头和雷达安装在机器人底座上，采集积渣信息；通过上位机进行视觉图像和雷达点云信息融合，分析获得渣石的位置信息；通过各关节处布置的传感器识别机械臂的当前位姿，进行清渣运动规划，并将各关节运动量发送至可编程逻辑控制器（programmable logic controller，PLC），控制机械臂调整位姿，最终实现渣石的清理。作业流程如图3所示。
图 3 清渣机器人作业流程Fig. 3 Operation flow chart of muck removal robot下载:
全尺寸图片
1.2 清渣机器人机构设计
采用以下方案进行清渣机器人的设计：
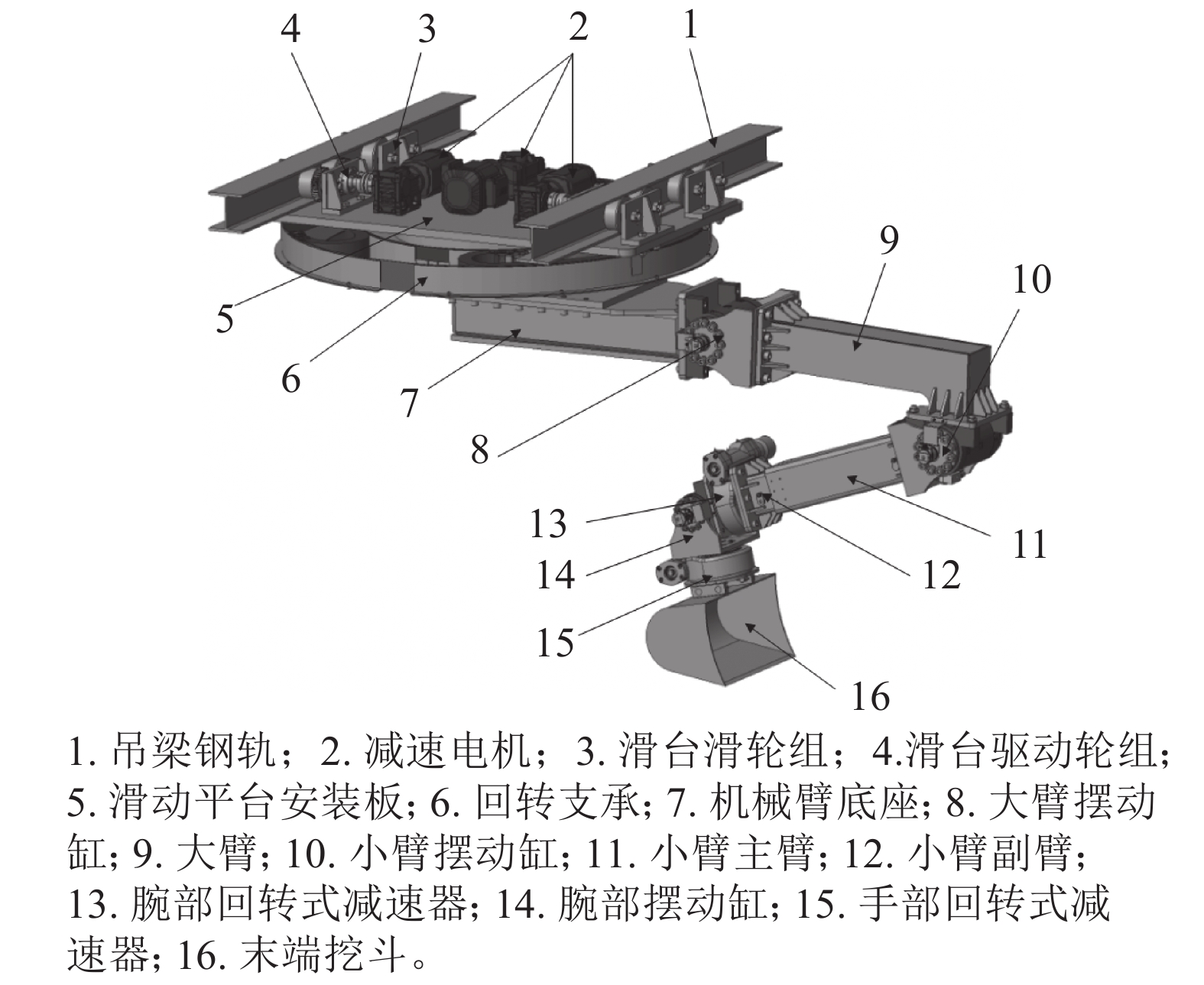
首先，根据清渣区域需求，所设计的清渣机器人需要沿着隧道轴线移动，能够进行回转、俯仰、挖渣等动作，因此，其自由度数目应不少于4个；此外，在清渣作业结束后，机械臂可折叠起来，不影响后续作业；针对机械臂作业安装限制、负载能力、防水、防尘和运动平稳性要求，选择电液混合驱动方案；针对机械臂的灵活性[10]要求，提出图4所示的新型机械臂结构。
图 4 清渣机器人本体机构Fig. 4 Body structure of muck removal robot下载:
全尺寸图片
如图4所示，清渣机器人安装在主梁下部，主要由行走装置和机械臂组成。行走装置主要由吊梁钢轨、减速电机、滑台轮滑组、滑台驱动轮组、滑动平台安装板、回转支承等组成。其中：吊梁钢轨采用两根“H”型钢对称布置；滑动平台上安装有滑轮安装座、驱动轮安装座、减速电机，实现机器人本体沿隧道轴向移动；回转支承连接滑动平台安装板与机械臂底座，通过减速电机实现机械臂整体转动。机械臂主要由机械臂底座、大臂摆动缸、大臂、小臂摆动缸、小臂主臂、小臂副臂、腕部回转式减速器、腕部摆动缸、手部回转式减速器、末端挖斗等组成。其中：大臂摆动缸实现大臂的俯仰；小臂摆动缸实现小臂的俯仰；小臂内置的直线油缸实现小臂的伸缩；小臂末端安装有腕部回转式减速器，实现腕部的回转；腕部摆动缸实现手部的俯仰；此外，末端安装回转式减速器，实现末端挖斗的翻转。
2. 清渣机器人建模与仿真
2.1 清渣机器人运动学建模
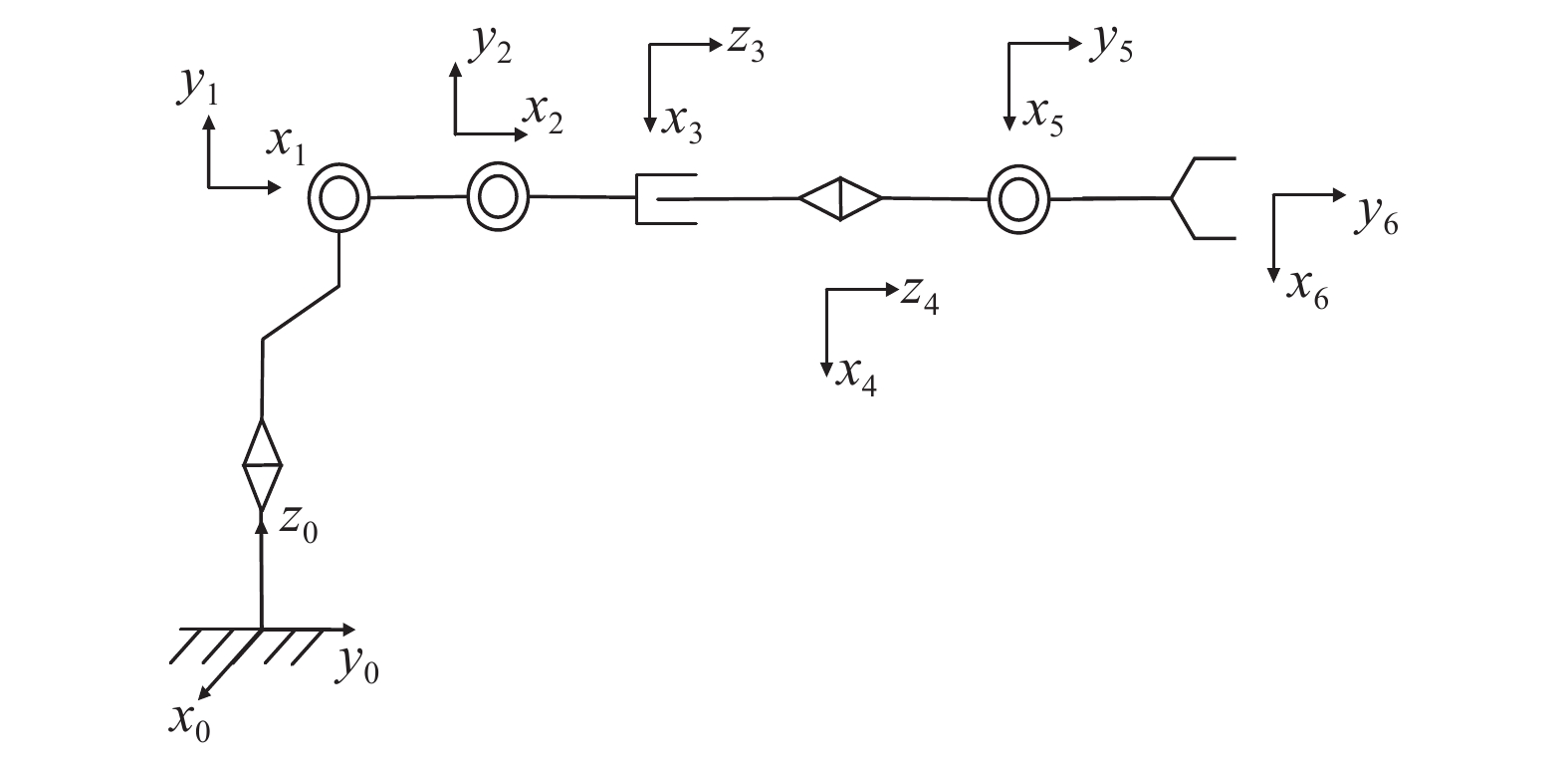
建立机器人的运动学模型是进行机器人运动分析、工作空间计算、运动控制的前提[11]。考虑到清渣机器人在吊梁钢轨上移动和手部回转对末端姿态没有影响，建模时不考虑这两个自由度。采用D–H参数法[12-13]，以回转支承轴线竖直向下为
${\textit{z}_0}$ 正方向，以隧道轴线向前为${x_0}$ 正方向，建立基坐标系；其他关节以转动轴线或伸缩方向为${\textit{z}_i}$ 轴，以${\textit{z}_i}$ 与${\textit{z}_{i - 1}}$ 的公垂线为${x_i}$ 轴，且以远离${\textit{z}_{i - 1}}$ 的方向为${x_i}$ 正方向，根据右手定则，确定${y_i}$ 轴正方向，最终建立坐标系，如图5所示，获得D–H参数如表1所示。表 1 清渣机器人D–H参数表Table 1 Denavit–Hartenberg parameters of muck removal robot连杆编号 转角θi/rad 偏距di/m 连杆长度ai/m 连杆扭角αi/rad 1 ${\theta _1}$ ${k_1}$ ${k_2}$ π/2 2 ${\theta _2}$ 0 ${k_3}$ 0 3 ${\theta _3}$ 0 0 –π/2 4 0 ${d_4}$ 0 0 5 ${\theta _5}$ ${k_4}$ 0 π/2 6 ${\theta _6}$ 0 ${k_5}$ 0 注： ${a_i}$为 ${{\textit{z}_i}}$与 ${{\textit{z}_{i - 1}}}$的公垂线长度； ${\alpha _i}$为 ${{\textit{z}_i}}$与 ${\textit{z}_{i - 1} }$之间的夹角； ${d_i}$为 ${x_i}$与 ${x_{i - 1}}$之间的距离； ${\theta _i}$为 ${x_i}$与 ${x_{i - 1}}$之间的夹角。 
图 5 清渣机器人连杆坐标系Fig. 5 Link coordinate system of muck removal robot下载:
全尺寸图片
2.1.1 正向运动学分析
根据建立的连杆坐标系，利用齐次变换矩阵
${}_i^{i - 1}{\boldsymbol{T}}$ 表示相邻连杆的几何关系：$$ {}^{i-1} {}_{i}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos\text{ }{\theta _i}}&{ - \cos\text{ }{\theta _i}\sin\text{ }{\theta _i}}&{\sin\text{ }{\alpha _i}\sin\text{ }{\theta _i}}&{{a_i}\cos\text{ }{\theta _i}} \\ {\sin\text{ }{\theta _i}}&{\cos\text{ }{\alpha _i}\cos\text{ }{\theta _i}}&{ - \sin\text{ }{\alpha _i}\cos\text{ }{\theta _i}}&{{a_i}\sin\text{ }{\theta _i}} \\ 0&{\sin\text{ }{\alpha _i}}&{\cos\text{ } {\alpha _i}}&{{d_i}} \\ 0&0&0&1 \end{array}} \right] $$ (1) 代入表1中的D–H参数，获得清渣机器人连杆间的变换矩阵
${}_1^0{\boldsymbol{T}}$ 、${}_2^1{\boldsymbol{T}}$ 、${}_3^2{\boldsymbol{T}}$ 、${}_4^3{\boldsymbol{T}}$ 、${}_5^4{\boldsymbol{T}}$ 、${}_6^5{\boldsymbol{T}}$ ，则末端挖斗的位姿可表示为：$$ {}_6^0{\boldsymbol{T}}{\text{ = }}{}_1^0{\boldsymbol{T}}{}_2^1{\boldsymbol{T}}{}_3^2{\boldsymbol{T}}{}_4^3{\boldsymbol{T}}{}_5^4{\boldsymbol{T}}{}_6^5{\boldsymbol{T}}{\text{ = }}\left| {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}} \\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}} \\ {{n_{\textit{z}}}}&{{o_{\textit{z}}}}&{{a_{\textit{z}}}}&{{p_{\textit{z}}}} \\ 0&0&0&1 \end{array}} \right| $$ (2) 式（2）中：
$$ {n_x}{{ = }}{{{{c}}}_{{6}}}{{(}}{{{{s}}}_{{1}}}{{{s}}_{{5}}}{{ - }}{{{c}}_{{5}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}{{ - }}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{c}}_{{3}}}{{)) + }}{{{s}}_{{6}}}{{(}}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{s}}_{{3}}}{{ + }}{{{c}}_{{1}}}{{{c}}_{{3}}}{{{s}}_{{2}}}{{)}},$$ $$ {n_y}{{ = }}{{{s}}_{{6}}}{{(}}{{{c}}_{{2}}}{{{s}}_{{1}}}{{{s}}_{{3}}}{{ + }}{{{c}}_{{3}}}{{{s}}_{{1}}}{{{s}}_{{2}}}{{) - }}{{{c}}_{{6}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{5}}}{{ + }}{{{c}}_{{5}}}{{(}}{{{s}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}{{ - }}{{{c}}_{{2}}}{{{c}}_{{3}}}{{{s}}_{{1}}}{{))}},$$ $$ {n_\textit{z}}{{ = }}{{{c}}_{{5}}}{{{c}}_{{6}}}{{{s}}_{23}}{{ - }}{{{s}}_{{6}}}{{{c}}_{23}}, $$ $$ {o_x}{{ = }}{{{c}}_{{6}}}{{(}}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{s}}_{{3}}}{{ + }}{{{c}}_{{1}}}{{{c}}_{{3}}}{{{s}}_{{2}}}{{) - }}{{{s}}_{{6}}}{{(}}{{{s}}_{{1}}}{{{s}}_{{5}}}{{ - }}{{{c}}_{{5}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}{{ - }}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{c}}_{{3}}}{{))}},$$ $$ {o_y}{{ = }}{{{s}}_{{6}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{5}}}{{ + }}{{{c}}_{{5}}}{{(}}{{{s}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}} {-}{{{c}}_{{2}}}{{{c}}_{{3}}}{{{s}}_{{1}}}{{)) + }}{{{c}}_{{6}}}{{(}}{{{c}}_{{2}}}{{{s}}_{{1}}}{{{s}}_{{3}}}{{ + }}{{{c}}_{{3}}}{{{s}}_{{1}}}{{{s}}_{{2}}}{{)}}, $$ $$ {o_{\textit{z}}}{{ = - }}{{{c}}_{{6}}}{{{c}}_{23}}{{ - }}{{{c}}_{{5}}}{{{s}}_{{6}}}{{{s}}_{23}},$$ $$ {a_x}{{ = - }}{{{c}}_{{5}}}{{{s}}_{{1}}}{{ - }}{{{s}}_{{5}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}{{ - }}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{c}}_{{3}}}{{)}}, $$ $$ {a_y}{{ = }}{{{c}}_{{1}}}{{{c}}_{{5}}}{{ - }}{{{s}}_{{5}}}{{(}}{{{s}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}{{ - }}{{{c}}_{{2}}}{{{c}}_{{3}}}{{{s}}_{{1}}}{{)}},$$ $$ {a_{\textit{z}}}{{ = }}{{{s}}_{{5}}}{{{s}}_{23}},$$ $$ \begin{aligned}[b] {p_x}{{ = }}&{k_2}{{{c}}_{{1}}}{{ + }}{k_3}{{{c}}_{{1}}}{{{c}}_{{2}}}{{ + }}{d_{{4}}}{{{s}}_{23}}{{{c}}_{{1}}}{{ + }}{k_5}{{{c}}_{{6}}}{{(}}{{{s}}_{{1}}}{{{s}}_{{5}}}{{ - }}{{{c}}_{{5}}}{{(}}{{{c}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}}- \hfill \\& {{ }}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{c}}_{{3}}}{{)) + }}{k_5}{{{s}}_{{6}}}{{{s}}_{{{23}}}}{{{c}}_1}{{ + }}{k_4}{{{c}}_{{1}}}{{{c}}_{{2}}}{{{s}}_{{3}}}{{ + }}{k_4}{{{c}}_{{1}}}{{{c}}_{{3}}}{{{s}}_{{2}}} ,\end{aligned} $$ $$ \begin{aligned}[b] {{p}_{y}}{=}&{{k}_{2}}{{{s}}_{{1}}}{+}{{k}_{3}}{{{c}}_{{2}}}{{{s}}_{{1}}}{+}{{d}_{{4}}}{{{s}}_{{23}}}{{{s}}_{1}}-{{k}_{5}}{{{c}}_{{6}}}{(}{{{c}}_{{1}}}{{{s}}_{{5}}}{+}{{{c}}_{{5}}}{(}{{{s}}_{{1}}}{{{s}}_{{2}}}{{{s}}_{{3}}} -\\ & { }{{{c}}_{{2}}}{{{c}}_{{3}}}{{{s}}_{{1}}}{))+}{{k}_{5}}{{{s}}_{{6}}}{{{s}}_{1}}{{{s}}_{23}}{+}{{k}_{4}}{{{c}}_{{2}}}{{{s}}_{{1}}}{{{s}}_{{3}}}{+}{{k}_{4}}{{{c}}_{{3}}}{{{s}}_{{1}}}{{{s}}_{{2}}}, \end{aligned} $$ $$ \begin{aligned}[b] {p_{\textit{z}}}{{ = }}&{k_{{3}}}{{{s}}_{{2}}}{{ - }}{k_{{4}}}{{{c}}_{{{23}}}}{{ + }}{k_{{5}}}{{(}}{{{c}}_{{5}}}{{{c}}_{{6}}}{{ + }}{{{s}}_{{5}}}{{{s}}_{{6}}}{{)}}{{{s}}_{{{23}}}}/2{{ - }}{d_{{4}}}{{{c}}_{23}} +\hfill \\& {{ }}{k_{{5}}}{{{c}}_{56}}{{{s}}_{23}}{{/2 - }}{k_{{5}}}{{{c}}_{{{23}}}}{{{s}}_{{{6 }}}}{{ + }}{k_{{1}}}； \end{aligned} $$ 其中，
${{{s}}_i}{\text{ = }}\sin\text{ } {\theta _i}\text{，}{{{c}}_i}{\text{ = }}\cos \text{ }{\theta _i}\text{，}{{{s}}_{mn}}{\text{ = }}\sin ({\theta _m}{\text{ + }}{\theta _n})\text{，} {{{c}}_{mn}}{\text{ = }}\cos ({\theta _m}{\text{ + }}{\theta _n}) $ 。2.1.2 逆向运动学分析
在实际控制过程，通过视觉与雷达系统分析计算出积渣的位置信息，需要通过逆运动学[14-15]求解清渣机进行姿态调整时的各关节变量。对于本文研究的隧道底部积渣清理机器人，其逆运动学可描述为：已知作业过程末端挖斗在基坐标系下位姿
${}_6^0{\boldsymbol{T}}$ ，求解关节变量${\theta _1}$ 、${\theta _2}$ 、${\theta _3}$ 、${d_4}$ 、${\theta _5}$ 、${\theta _6}$ 。本文采用解析法[16]将关节变量分离出来进行求解，其具体过程如下：1）
${\theta _1}$ 的求解将式（2）两端同时左乘
${}_1^0{\boldsymbol{T}}$ 的逆矩阵${}_1^0{{\boldsymbol{T}}^{ - 1}}$ ，右乘${}_6^5{\boldsymbol{T}}$ 的逆矩阵${}_6^5{{\boldsymbol{T}}^{ - 1}}$ ，得：$$ {}_1^0{{\boldsymbol{T}}^{ - 1}}{}_6^0{\boldsymbol{T}}{}_6^5{{\boldsymbol{T}}^{ - 1}}{\text{ = }}{}_2^1{\boldsymbol{T}}{}_3^2{\boldsymbol{T}}{}_4^3{\boldsymbol{T}}{}_5^4{\boldsymbol{T}} $$ (3) 根据式（3）展开后第3行、第4列元素相等，可得：
$$ {k_{\text{5}}}{n_y}{{c}_{\text{1}}}{{ - }}{p_y}{{{c}}_{\text{1}}}{{ - }}{k_{\text{5}}}{n_x}{{{s}}_{\text{1}}}{\text{ + }}{p_x}{{{s}}_{\text{1}}}{\text{ = 0}}。 $$ a.当
${{k}_{\text{5}}}{{n}_{y}}{-}{{p}_{y}}=0 $ 时，若${{k}_{\text{5}}}{{n}_{x}}{-}{{p}_{x}}>0 $ ，${{\theta }_{1}} $ =0°；若${{k}_{\text{5}}}{{n}_{x}}- {{p}_{x}} < 0$ ，${{\theta }_{1}} $ =180°。b.当
${{k}_{\text{5}}}{{n}_{x}}{-}{{p}_{x}}=0 $ 时，${{\theta }_{1}} $ =90°。c.其他情况，解得：
$$ {{\theta }_{1}}\text{=arctan}\frac{{{k}_{\text{5}}}{{n}_{y}}\text{-}{{p}_{y}}}{{{k}_{\text{5}}}{{n}_{x}}\text{-}{{p}_{x}}} 。$$ 2）
${\theta _5}$ 的求解根据式（3）展开后第3行、第3列元素相等，可得：
$$ {{ - }}{{{c}}_{{5}}}{{ = }}{a_x}{{{s}}_{{1}}}{{ - }}{a_y}{{{c}}_{{1}}}， $$ 解得：
$$ {\theta _{\text{5}}}{\text{ = }} \pm {\text{arccos}}\left( {{a_y}{{{c}}_{\text{1}}} - {a_x}{{{s}}_{\text{1}}}} \right)。 $$ 3）
${\theta _6}$ 的求解根据式（3）展开后第3行、第2列元素相等，可得：
$$ {{ - }}{{{s}}_{{6}}}{{(}}{n_y}{{{c}}_{{1}}}{{ - }}{n_x}{{{s}}_{{1}}}{{) - }}{{{c}}_{{6}}}{{(}}{o_y}{{{c}}_{{1}}}{{ - }}{o_x}{{{s}}_{{1}}}{{) = 0}}。 $$ a.当
${{o}_{y}}{{{c}}_{\text{1}}}{-}{{o}_{x}}{{{s}}_{\text{1}}}=0$ 时，若${-}{{n}_{y}}{{{c}}_{\text{1}}}\text{+}{{n}_{x}}{{{s}}_{\text{1}}} > 0$ ，${{\theta }_{6}} $ =0°；若${-}{{n}_{y}}{{{c}}_{\text{1}}}\text{+}{{n}_{x}}{{{s}}_{\text{1}}} < 0$ ，${{\theta }_{6}} $ =180°。b.当
${-}{{n}_{y}}{{{c}}_{\text{1}}}\text{+}{{n}_{x}}{{{s}}_{\text{1}}}=0$ 时，${{\theta }_{6}} $ =90°。c.其他情况，解得：
$$ {{\theta }_{6}}\text{=arctan}\frac{{{o}_{y}}{{{c}}_{\text{1}}}{-}{{o}_{x}}{{{s}}_{1}}}{-{{n}_{y}}{{{c}}_{\text{1}}}\text{+}{{n}_{x}}{{{s}}_{\text{1}}}}。 $$ 4）
${d_4}$ 的求解将式（2）两端依次左乘
${}_1^0{{\boldsymbol{T}}^{ - 1}}$ ，右乘${}_6^5{{\boldsymbol{T}}^{ - 1}}$ 、${}_5^4{{\boldsymbol{T}}^{ - 1}}$ 、${}_4^3{{\boldsymbol{T}}^{ - 1}}$ ，得：$$ {}_1^0{{\boldsymbol{T}}^{ - 1}}{}_6^0{\boldsymbol{T}}{}_6^5{{\boldsymbol{T}}^{ - 1}}{}_5^4{{\boldsymbol{T}}^{ - 1}}{}_4^3{{\boldsymbol{T}}^{ - 1}}{\text{ = }}{}_2^1{\boldsymbol{T}}{}_3^2{\boldsymbol{T}} $$ (4) 根据式（4）展开后第3行、第4列元素相等，可得：
$$\begin{gathered} {k_{{4}}}{{{s}}_{{6}}}{{(}}{n_y}{{{c}}_{{1}}}{{ - }}{n_x}{{{s}}_{{1}}}{{) + }}{d_{{4}}}{{(}}{{{s}}_{{6}}}{{(}}{n_y}{{{c}}_{{1}}}{{ - }}{n_x}{{{s}}_{{1}}}{{) + }}{{{c}}_{{6}}}{{(}}{o_y}{{{c}}_{{1}}}{{ - }}{o_x}{{{s}}_{{1}}}{{))}}+ \hfill \\ \quad {k_{{5}}}{n_y}{{{c}}_{{1}}}{{ - }}{p_y}{{{c}}_{{1}}}{{ - }}{k_5}{n_x}{{{s}}_{{1}}}{{ + }}{p_x}{{{s}}_{{1}}}{{ + }}{k_4}{{{c}}_{{6}}}{{(}}{o_y}{{{c}}_{{1}}}{{ - }}{o_x}{{{s}}_{{1}}}{{) = 0}}， \end{gathered}$$ 解得：
$$ \begin{aligned}[b] {d_4} =& {{ - }}(({k_4}{{{s}}_{{6}}}{{(}}{n_y}{{{c}}_{{1}}}{{ - }}{n_x}{{{s}}_{{1}}}{{)}} + {{(}}{k_{{5}}}{n_y}{{{c}}_{{1}}}{{ - }}{p_y}{{{c}}_{{1}}}{{ - }}{k_{{5}}}{n_x}{{{s}}_{{1}}}{{ + }}{p_x}{{{s}}_{{1}}}+ \hfill \\& {k_4}{{{c}}_{{6}}}{{(}}{o_y}{{{c}}_{{1}}}{{ - }}{o_x}{{{s}}_{{1}}}{{))}})/({{{s}}_{{6}}}{{(}}{n_y}{{{c}}_{{1}}}{{ - }}{n_x}{{{s}}_{{1}}}{{)}}+ {{{c}}_{{6}}}{{(}}{o_y}{{{c}}_{{1}}}{{ - }}{o_x}{{{s}}_{{1}}}{{)}})) 。 \end{aligned} $$ 5）
${\theta _2}$ 的求解根据式（4）展开后第2行、第4列元素相等，可得：
$$ {k_3}{s_{\text{2}}}{\text{ = }}{p_{\textit{z}}}{{ - }}{k_{\text{5}}}{n_{\textit{z}}}{d_{\text{4}}}{\text{(}}{o_{\textit{z}}}{{{c}}_{\text{6}}}{\text{ + }}{n_{\textit{z}}}{{{s}}_{\text{6}}}{{) - }}{k_4}{o_{\textit{z}}}{{{c}}_{\text{6}}}{{ - }}{k_4}{n_{\textit{z}}}{{{s}}_{\text{6}}}{{ - }}{k_1}， $$ 解得：
$$ \;{\theta }_{\text{2}}\text=\mathrm{arcsin}(({p}_{{\textit{z}}}-{k}_{\text{5}}{n}_{{\textit{z}}}{d}_{\text{4}}\text{(}{o}_{{\textit{z}}}{{c}}_{\text{6}}\text+{n}_{{\textit{z}}}{{s}}_{\text{6}}{)-}{k}_{4}{o}_{{\textit{z}}}{{c}}_{\text{6}} {-}{k}_{4}{n}_{{\textit{z}}}{{s}}_{\text{6}}-{k}_{1})\text{/}{k}_{3}) 。$$ 6）
${\theta _3}$ 的求解根据式（4）展开后第2行、第1列元素相等，可得：
$$ {{{s}}_{{\text{23}}}}{\text{ = }}{a_{\textit{z}}}{{{s}}_{\text{5}}}{\text{ + }}{{{c}}_{\text{5}}}{\text{(}}{n_{\textit{z}}}{{{c}}_{\text{6}}}{{ - }}{o_{\textit{z}}}{{{s}}_{\text{6}}}{\text{)}}， $$ 解得：
$$ {\theta _{{3}}}{{ = \text=\mathrm{arcsin(}}}{a_{\textit{z}}}{{{s}}_{{5}}}{{ + }}{{{c}}_{{5}}}{{(}}{n_{{\textit{z}}}}{{{c}}_{{6}}}{{ - }}{o_{{\textit{z}}}}{{{s}}_{{6}}}{{)) - }}{\theta _{{2}}}。 $$ 综上，即可获得清渣机器人要到达任意位姿时的所有逆解。
2.1.3 最优解选取
通过逆运动学求解获得机器人在目标姿态下的多组逆解，根据最短行程原则对其进行加权选择。
首先，由于实际运动过程中，各关节都有一定的运动范围限制，因此，将超出关节范围的逆解删除；然后，将满足关节运动范围的逆解与机器人上一姿态的关节变量做差；由于清渣机器人前3个连杆较大，后3个连杆较小，其运动代价不同，因此，依据“多移动小连杆，少移动大连杆”的原则，对各关节变量的差值进行加权，选择总运动代价最小的一组作为最优解，即：
$$ \min \sum\limits_{i = 1}^6 {\left| {{f_i}{{\mathit{\Delta}} _i}} \right|} $$ (5) 式中，
${f_i}$ 为$i$ 连杆变量的加权系数，${{\mathit{\Delta}} _i}$ 为$i$ 关节与上一姿态关节变量的差值。2.2 工作空间求解
工作空间是清渣机器人能否完成具体任务的判断依据。设计的隧道底部积渣清理机器人实际尺寸为k1=0.58 m，k2=1.038 m，k3=1.081 9 m，k4=0.107 m，k5=0.666 6 m，
${d_4}$ 取值范围为1.035～1.415 m。基于蒙特卡罗法[17]求解其工作空间，借助MATLAB软件，获得清渣机器人工作空间如图6所示。
图 6 清渣机器人末端工作空间Fig. 6 Workspace of end effector of muck removal robot下载:
全尺寸图片
图6中，X轴正方向表示隧道的轴向方向，Y轴正方向表示水平方向，Z轴正方向表示隧道竖直向下方向。从图6（b）、（d）获得清渣机器人末端挖斗的最大作业深度为3 830 mm，且满足隧道底部±45°的作业范围需求。
2.3 控制器设计
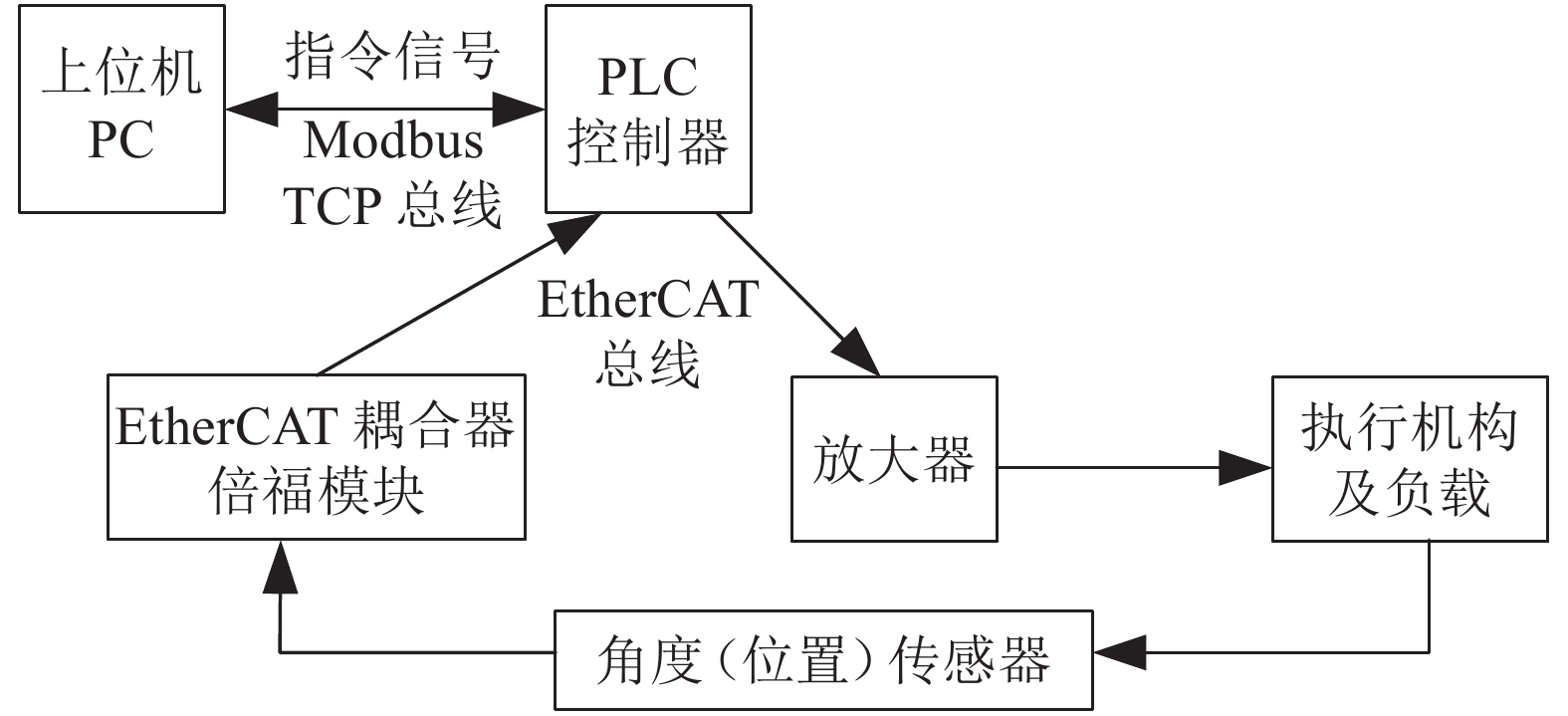
清渣机械臂采用液压驱动方案，电气系统如图7所示。上位机采用LabVIEW设计，进行清渣机器人运动规划并产生指令信号；上位机PC通过Modbus TCP总线与PLC控制器通信，PLC控制器通过EtherCAT总线与放大器相连；放大器收到PLC控制器的输出信号，继而驱动比例阀组，控制执行机构带动机器人各关节负载按给定指令运动；各关节传感器将当前角度（位置）信号通过EtherCAT总线反馈给PLC控制器。
图 7 清渣机器人电气框图Fig. 7 Electrical block diagram of muck removal robot下载:
全尺寸图片
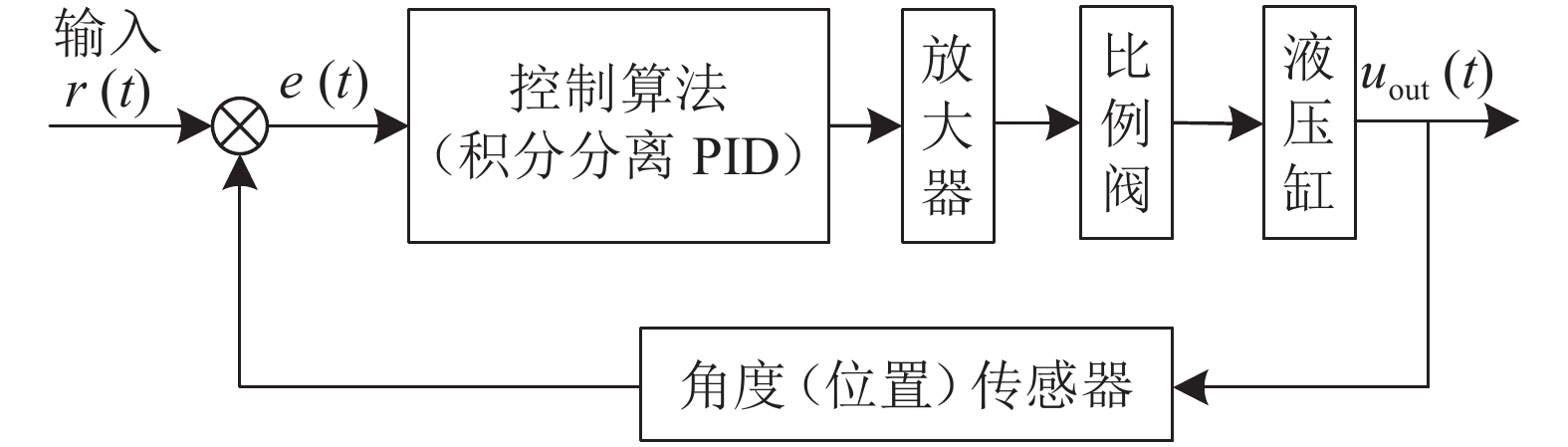
图7中的执行机构采用电液比例位置控制系统，其每个液压执行元件、对应的关节负载及相应的控制算法构成一个独立的位置控制系统。以液压缸为例，其控制框图如图8所示。
图 8 单关节位置控制框图Fig. 8 Block diagram of single joint control下载:
全尺寸图片
由于传统PID控制算法积分环节对偏差的积累作用存在着积分饱和的缺点[18]，从而引起输出过大超调，甚至导致系统剧烈振荡的问题，因此，清渣机器人采用积分分离PID[19-20]的控制算法。其基本思路为：当机器人各关节给定值与实际输出反馈值存在很大误差（大于设定阈值）时，取消积分作用，避免积分作用累积导致系统超调量增大，降低其稳定性；当传感器输出反馈值接近关节的给定值时，引入积分环节，提高清渣机器人控制精度。
积分分离PID控制算法如下：
$$ {u}_{{{\rm{out}}}}(t)=\left\{ \begin{array}{l}{K}_{{\rm{p}}}\left[e\left(t\right)+\dfrac{1}{{T}_{{\rm{i}}}}{{\displaystyle} {\displaystyle\int }_{0}^{t}e\left(t\right)\text{d}t}+\dfrac{{T}_{{\rm{d}}}\text{d}e\left(t\right)}{\text{d}t}\right]\text{}\text{ }\text{, }\left|e\right|\le \varepsilon \text{ }\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{;}\\ {K}_{{\rm{p}}}\left[e\left(t\right)+\dfrac{{T}_{{\rm{d}}}\text{d}e\left(t\right)}{\text{d}t}\right]\text{, }\left|e\right| > \varepsilon \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\end{array}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\right. $$ (6) 式中，
$ e\left( t \right) $ 为位置（角度）误差，${K_{\rm{p}}}$ 、${T_{\rm{i}}}$ 、${T_{\rm{d}}}$ 分别为比例系数、积分时间和微分时间，$\varepsilon $ 为积分分离点。3. 样机试验
3.1 试验平台搭建
以开挖直径6 400 mm的TBM为搭载对象，搭建隧道底部积渣清理机器人试验平台，如图9所示。
图 9 清渣机器人试验平台Fig. 9 Test platform of the muck removal robot下载:
全尺寸图片
3.2 控制器试验与结果分析
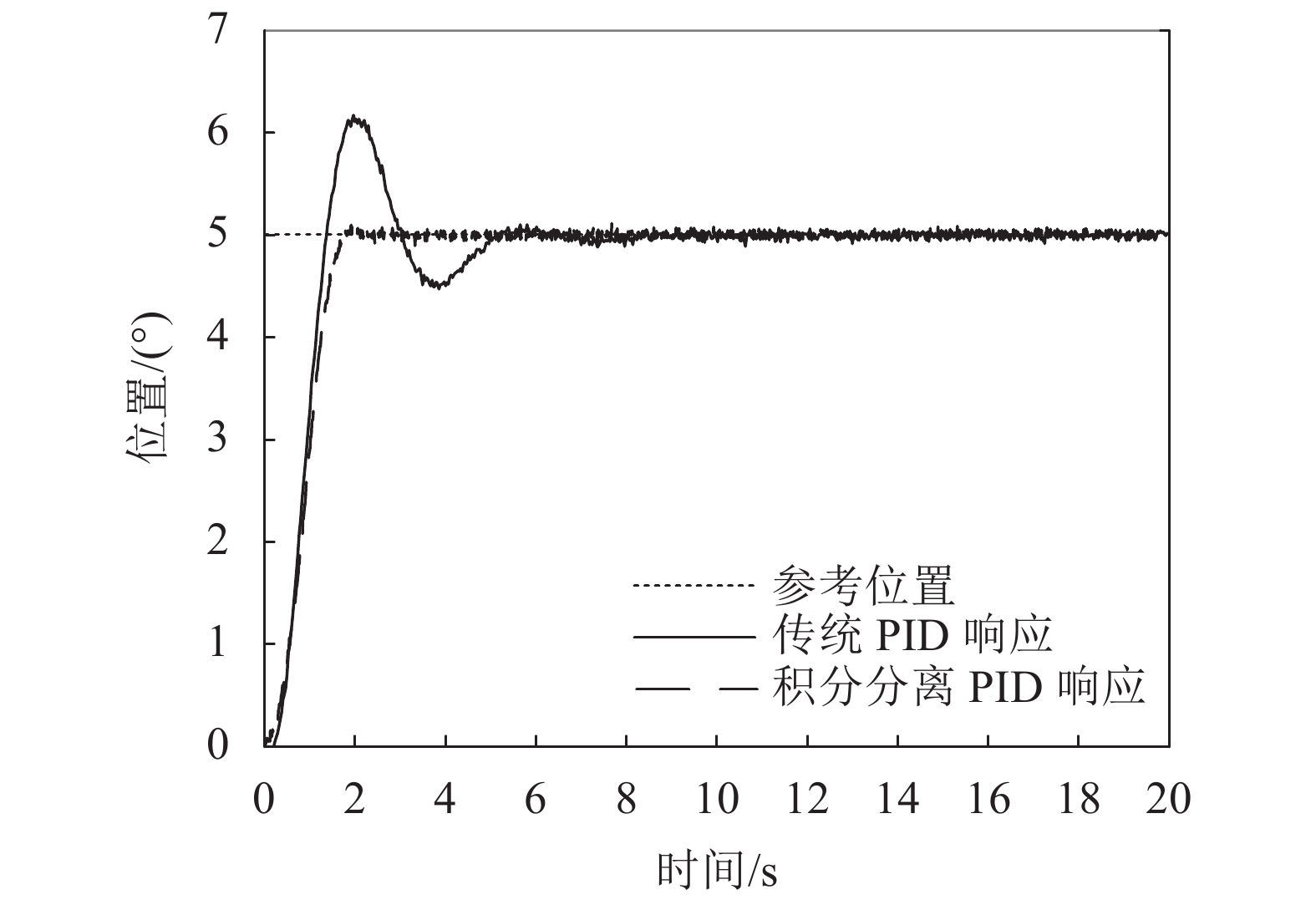
为验证积分分离PID算法的有效性，设计传统PID和积分分离PID两种控制算法位置跟踪对比试验。机械臂6个关节的位置控制算法相同，以第4个关节为例，设定5°的阶跃信号，两种算法相关参数均设置为
${K_{\rm{p}}} = 20$ ，${T_{\rm{i}}} = 0.5$ ，${T_{\rm{d}}} = 0$ ，积分分离PID的积分分离点$\varepsilon $ 设置为1°，获得阶跃响应结果如图10所示。
图 10 两种算法下的试验结果Fig. 10 Experimental results under two algorithms下载:
全尺寸图片
由图10可知：传统PID和积分分离PID均可实现关节的稳定控制，但传统的PID控制超调量较大，其超调达到21.3%；采用积分分离PID控制，当误差量大于1°时，积分环节并未起到作用，所以其积分环节仅在接近参考信号时才起作用，超调量较小，仅在2.6%以内，降低了18.7%。
3.3 隧道底部积渣清理试验
基于搭建的试验台，在模拟隧道底部放置渣石，机器人进行底部积渣清理，获得清渣机器人作业过程如图11所示。
图 11 清渣机器人清渣试验Fig. 11 Muck removal test of muck removal robot下载:
全尺寸图片
图11（a）为抓渣起始姿态，机器人末端运动至渣土处，准备进行渣土抓取；图11（b）和（c）为机器人抓渣后的运动姿态，机器人抓取渣土后，沿着隧道洞壁进行运渣；图11（d）为倒渣姿态，此时机器人末端挖斗运动至主梁上方，挖斗翻转，将渣土倾倒，完成单次清渣作业。清渣机器人沿着运动路径，能够在53 s完成单次清渣作业，并且机器人运动平稳，无较大的抖动现象。以直径为6 400 mm的隧道为例，按照较差工况，渣石的积攒厚度为0.5 m，隧道方向长度为0.5 m时，渣石总体积约为0.698 4 m3；按照斗容0.04 m³，约需挖掘15次（约13.25 min），满足16 min的需求。证明了清渣方案的可行性，以及机构和控制系统设计的合理性和清渣的高效。
该技术成果已应用于粤海引水项目、川藏项目；其中，搭载清渣机的“雪域先锋”号TBM于2021年8月12日顺利抵达西藏林芝项目工地，如图12所示。
图 12 “雪域先锋”号TBM清渣机Fig. 12 Muck removal robot of Xueyuxianfeng TBM下载:
全尺寸图片
4. 结 论
1）针对隧道施工对隧道底部积渣清理的自动化、智能化需求，提出一种基于视觉和雷达的机器人清渣方案；同时，设计了一种新型清渣机器人系统，通过工作空间计算，表明该机构满足作业范围要求。
2）为实现清渣机器人作业最优控制效果，针对所设计的清渣机器人，进行积分分离PID控制器设计，解决了位置误差累积引起的关节抖动问题。
3）搭建了清渣机器人试验平台，进行室内试验，结果显示，所设计清渣机器人能够快速、高效地完成隧道底部积渣清理作业。
-
图 1 清渣实际工况
Fig. 1 Actual working condition of muck removal
下载:
全尺寸图片
图 2 隧道清渣区域示意图
Fig. 2 Schematic diagram of muck removal area in tunnel
下载:
全尺寸图片
图 3 清渣机器人作业流程
Fig. 3 Operation flow chart of muck removal robot
下载:
全尺寸图片
图 4 清渣机器人本体机构
Fig. 4 Body structure of muck removal robot
下载:
全尺寸图片
图 5 清渣机器人连杆坐标系
Fig. 5 Link coordinate system of muck removal robot
下载:
全尺寸图片
图 6 清渣机器人末端工作空间
Fig. 6 Workspace of end effector of muck removal robot
下载:
全尺寸图片
图 7 清渣机器人电气框图
Fig. 7 Electrical block diagram of muck removal robot
下载:
全尺寸图片
图 8 单关节位置控制框图
Fig. 8 Block diagram of single joint control
下载:
全尺寸图片
图 9 清渣机器人试验平台
Fig. 9 Test platform of the muck removal robot
下载:
全尺寸图片
图 10 两种算法下的试验结果
Fig. 10 Experimental results under two algorithms
下载:
全尺寸图片
图 11 清渣机器人清渣试验
Fig. 11 Muck removal test of muck removal robot
下载:
全尺寸图片
图 12 “雪域先锋”号TBM清渣机
Fig. 12 Muck removal robot of Xueyuxianfeng TBM
下载:
全尺寸图片
表 1 清渣机器人D–H参数表
Table 1 Denavit–Hartenberg parameters of muck removal robot
连杆编号 转角θi/rad 偏距di/m 连杆长度ai/m 连杆扭角αi/rad 1 ${\theta _1}$ ${k_1}$ ${k_2}$ π/2 2 ${\theta _2}$ 0 ${k_3}$ 0 3 ${\theta _3}$ 0 0 –π/2 4 0 ${d_4}$ 0 0 5 ${\theta _5}$ ${k_4}$ 0 π/2 6 ${\theta _6}$ 0 ${k_5}$ 0 注： ${a_i}$为 ${{\textit{z}_i}}$与 ${{\textit{z}_{i - 1}}}$的公垂线长度； ${\alpha _i}$为 ${{\textit{z}_i}}$与 ${\textit{z}_{i - 1} }$之间的夹角； ${d_i}$为 ${x_i}$与 ${x_{i - 1}}$之间的距离； ${\theta _i}$为 ${x_i}$与 ${x_{i - 1}}$之间的夹角。 -
[1] 卢春房,蔡超勋.川藏铁路工程建设安全面临的挑战与对策[J].Engineering,2019,5(5):49–61. Lu Chunfang,Cai Chaoxun.Challenges and countermeasures for construction safety during the Sichuan—Tibet railway project[J].Engineering,2019,5(5):49–61 [2] 杜闯东,周路军,朵生君,等.川藏铁路隧道TBM适应性选型分析及不良地质对策与思考[J].隧道建设,2021,41(6):897–912. Du Chuangdong,Zhou Lujun,Duo Shengjun,et al.Consideration of TBM adaptability and selection for Sichuan—Tibet railway tunnels and countermeasures for unfavorable geologies[J].Tunnel Construction,2021,41(6):897–912 [3] 刘卓.川藏铁路全断面掘进机穿越断层破碎带隧道施工研究[J].中国工程机械学报,2019,17(3):263–267. Liu Zhuo.Research on tunnel boring machine construction of fault fracture zone in Sichuan—Tibet railway tunnel[J].Chinese Journal of Construction Machinery,2019,17(3):263–267 [4] 徐正宣,张利国,蒋良文,等.川藏铁路雅安至林芝段工程地质环境及主要工程地质问题[J].工程科学与技术,2021,53(3):29–42. Xu Zhengxuan,Zhang Liguo,Jiang Liangwen,et al.Engineering geological environment and main engineering geological problems of Ya’an—Linzhi section of the Sichuan—Tibet railway[J].Advanced Engineering Sciences,2021,53(3):29–42 [5] 高帅坡,陈立春,梁明剑,等.鲜水河断裂带康定城南新榆林探槽组揭露的破裂特征与地震复发行为[J].工程科学与技术,2021,53(3):53–61. Gao Shuaipo,Chen Lichun,Liang Mingjian,et al.Rupture characteristics and seismic recurrence behaviors of Xianshuihe fault revealed by Xinyulin trenches,south of Kangding[J].Advanced Engineering Sciences,2021,53(3):53–61 [6] 司景钊,曾云川,刘建兵.复杂地质铁路隧道敞开式TBM施工挑战及思考[J].隧道建设,2021,41(3):433–440. Si Jingzhao,Zeng Yunchuan,Liu Jianbing.Challenges and some thoughts on open-TBM construction in a railway tunnel with complex geologies[J].Tunnel Construction,2021,41(3):433–440 [7] 陈馈,冯欢欢,贺飞.川藏铁路TBM隧道建设挑战及装备创新设计探讨[J].隧道建设,2021,41(2):165–174. Chen Kui,Feng Huanhuan,He Fei.Challenges in tunnel construction and preliminary study on innovative TBM design for Sichuan—Tibet railway[J].Tunnel Construction,2021,41(2):165–174 [8] 安仓,曾绍毅,张浩波,等.一种敞开式TBM半自动底拱清渣系统:CN209621329U[P].2019−11−12. [9] 原晓伟,卓兴建,姜礼杰,等.TBM清渣机器人机构及其轨迹规划方法研究[J].隧道建设,2021,41(8):1422–1427. Yuan Xiaowei,Zhuo Xingjian,Jiang Lijie,et al.A new type of robotic structure and its trajectory planning method for tunnel boring machine muck removal[J].Tunnel Construction,2021,41(8):1422–1427 [10] 吴伟国.面向作业与人工智能的仿人机器人研究进展[J].哈尔滨工业大学学报,2015,47(7):1–19. doi: 10.11918/j.issn.0367-6234.2015.07.001 Wu Weiguo.Research progress of humanoid robots for mobile operation and artificial intelligence[J].Journal of Harbin Institute of Technology,2015,47(7):1–19 doi: 10.11918/j.issn.0367-6234.2015.07.001 [11] 吕志忠,张成维,钟功祥,等.一种四足磁吸附爬壁机器人运动学分析及仿真[J].工程科学与技术,2020,52(2):121–129. Lyu Zhizhong,Zhang Chengwei,Zhong Gongxiang,et al.Kinematics analysis and simulation of a quadruped magnetic adsorption wall-climbing robot[J].Advanced Engineering Sciences,2020,52(2):121–129 [12] Gleiss A C,Schallert R J,Dale J J,et al.Direct measurement of swimming and diving kinematics of giant Atlantic bluefin tuna(Thunnus thynnus)[J].Royal Society Open Science,2019,6(5):190203. doi: 10.1098/rsos.190203 [13] Yang Chunjie,Li Jianjun,Yang Xiuzhi.Direct kinematics of 6-RSPS driving simulation platform based on FBGS algorithm[J].Applied Mechanics & Materials,2017,865:474–479. [14] Alebooyeh M,Urbanic R J.Neural network model for identifying workspace,forward and inverse kinematics of the 7–DOF YuMi 14000 ABB collaborative robot[J].IFAC-PapersOnLine,2019,52(10):176–181. doi: 10.1016/j.ifacol.2019.10.019 [15] Ahmed E S,Elhosseini M A,Haikal A Y.A new ABC variant for solving inverse kinematics problem in 5 DOF robot arm[J].Applied Soft Computing,2018,73:24–38. doi: 10.1016/j.asoc.2018.08.028 [16] 覃艳明,赵静一,仝少帅,等.八自由度机械臂位置运动学模型解析解[J].农业机械学报,2019,50(1):400–405. Qin Yanming,Zhao Jingyi,Tong Shaoshuai,et al.Analytical solution of kinematics model of eight-degree-of-freedom manipulator[J].Transactions of the Chinese Society for Agricultural Machinery,2019,50(1):400–405 [17] 冷舒,吴克,居鹤华.机械臂运动学建模及解算方法综述[J].宇航学报,2019,40(11):1262–1273. doi: 10.3873/j.issn.1000-1328.2019.11.002 Leng Shu,Wu Ke,Ju Hehua.Overview of manipulator kinematics modeling and solving method[J].Journal of Astronautics,2019,40(11):1262–1273 doi: 10.3873/j.issn.1000-1328.2019.11.002 [18] 徐振邦,赵智远,贺帅,等.机器人工作空间求解的蒙特卡洛法改进和体积求取[J].光学精密工程,2018,26(11):2703–2713. doi: 10.3788/OPE.20182611.2703 Xu Zhenbang,Zhao Zhiyuan,He Shuai,et al.Improvement of monte carlo method for robot workspace solution and volume calculation[J].Optics and Precision Engineering,2018,26(11):2703–2713 doi: 10.3788/OPE.20182611.2703 [19] 曹法立,付远明,吴江涛.基于多级积分分离PID算法的温度控制系统[J].控制工程,2017,24(6):1107–1112. Cao Fali,Fu Yuanming,Wu Jiangtao.Temperature control system based on the multi-stage integral separation PID algorithm[J].Control Engineering of China,2017,24(6):1107–1112 [20] Jia Lin,Zhao Xinqiu.An improved particle swarm optimization(PSO) optimized integral separation PID and its application on central position control system[J].IEEE Sensors Journal,2019,19(16):1–8. doi: 10.1109/JSEN.2019.2912694
