Attention-based Remaining Useful Lifetime Prediction Method for Industrial Internet of Things
-
摘要: 设备剩余使用寿命预测作为工业物联网实现工业智能的重要功能之一，可基于设备的健康监测数据对其未来退化状态进行预测，以获得设备丧失运行能力前的剩余使用时间，从而制定相应的预测性维修策略，提升工业物联网设备的可靠性、可用性和安全性。提出一种基于注意力机制的设备剩余使用寿命预测方法（attention-based remaining useful lifetime prediction，ARULP）。首先，在模型训练阶段设计了一种局部注意力计算算法，构建数据驱动的局部注意力计算模型，采用训练数据计算局部注意力度量，从而获取预测模型关注的大量数据中关键信息的能力；然后，设计了一种基于局部注意力的相关向量机，通过在其隐变量学习过程中引入局部注意力机制，动态更新注意力权重，从而自适应地调整设备的状态预测模型，提升设备的剩余使用寿命预测精度；最后，在模型预测阶段，利用所构建的预测模型进行设备工作状态预测，并计算设备的剩余使用寿命。基于西安交通大学滚动轴承加速寿命试验数据集，与RVM、AR、ARIMA和LSTM 4个基准方法进行性能比较。结果表明，ARULP方法在不同工况下针对轴承外圈故障、内圈故障和保持架故障进行预测时均与轴承实际退化数据最为接近，能够较好地反映故障轴承的退化状态，最终实现对工业物联网设备剩余使用寿命进行高精度的预测。Abstract: As one of the important functions to realize industrial intelligence in Industrial Internet of Things (IIoT), remaining useful lifetime (RUL) prediction can predict the future degradation states of industrial equipment based on monitoring data and then reckon its remaining service time. Furthermore, the corresponding predictive maintenance strategies can be formulated in advance, and the reliability, availability, and safety of the equipment can be enhanced. In this paper, an attention-based remaining useful lifetime prediction method (ARULP) for IIoT was proposed. Firstly, in the model training stage, a local attention computation algorithm was designed by constructing a data-driven local attention computation model and utilizing the training data to compute the local attention measurements. Thus, the prediction model can pay more attention to the key information within a large amount of data. Then, a relevance vector machine based on local attention was designed by introducing the local attention mechanism into the learning process of implicit variables in the prediction model. The attention weights were updated to adjust the state prediction model adaptively and improve the prediction accuracy of the RUL for IIoT device. Finally, the ARULP method was applied in the model prediction stage to predict the degradation status and reckon the RUL for IIoT device. Extensive experiments based on the dataset of life test for accelerated rolling element bearings released by Xi’an Jiaotong University were carried out to predict the RUL for bearings with outer ring failure, inner ring failure, and holder failure under different working conditions. The experiment results showed that the prediction data of the ARULP method are the closest to the actual bearing degradation data and more accurate RUL prediction results can be obtained compared with RVM, AR, ARIMA, and LSTM benchmarks.
-
随着“工业4.0”与“中国制造2025”等概念的提出，工业物联网（Industrial Internet of Things，IIoT）已取得长足发展，并被广泛应用于智能制造、交通运输、能源管控等多个领域[1]。通过将具有感知和控制能力的传感器和执行器部署于机械装备和工业现场中，利用无线通信或现场总线技术传输监控数据，并采用机器学习方法实现数据驱动的智能化感知和控制，可以有效地提升工业生产效率，降低运维成本，提高产品质量，最终实现工业智能化[2]。
作为工业物联网的重要组成部分，故障预测与健康管理（prognostics health management，PHM）可基于设备的健康监测数据实现智能故障诊断和剩余使用寿命预测，并结合可用维修资源和设备使用需求制定最优的健康管理策略[3]。其中，设备剩余使用寿命预测可基于多种预测方法对工业物联网设备的未来性能进行预测，以获得设备在其丧失运行能力之前的剩余时间，并在设备出现故障前制定最优维修策略，改进维修计划，从而降低设备的维修成本，提高设备的可靠性、可用性和安全性[4]。
近年来，设备剩余使用寿命预测引起了学术界和工业界的极大关注，已广泛应用于工业物联网中的机械部件[5]、电子装置[6]、机电系统[7]的监控预测中。目前，主流的剩余使用寿命预测方法根据技术路线的差异可分为基于物理模型的预测方法和数据驱动的预测方法两类[8]。
基于物理模型的预测方法主要基于故障机理和经验知识来构建工业设备的退化模型并进行预测，典型的方法包括：基于Paris–Erdogan疲劳模型的预测方法[9]，基于Forman–Kearney–Engle模型的预测方法[10]，基于维纳过程、伽马过程或逆高斯过程[11]等随机过程的预测方法[12]等。该类预测方法适用于结构简单、工况单一的部件剩余寿命预测，而对于结构和工况较为复杂的工业物联网设备预测较为困难。
数据驱动的预测方法通过采集工业设备的各种监测数据，利用机器学习算法自动推断出隐藏在退化数据中的因果关系，从而构建复杂的机械设备退化模型。根据采用的学习方法不同，数据驱动的预测方法大致可分为基于回归的预测方法、基于人工神经网络的预测方法和基于相关向量机的预测方法等。其中，基于回归的预测方法通过利用差分消除数据波动，从而构建统计模型以拟合退化时序数据，代表性的预测模型包括自回归（autoregressive，AR）模型、自回归移动平均（auto-regressive integrated moving average，ARIMA）模型[13]和高斯过程回归（Gaussian process regression，GPR）模型[14]等。基于人工神经网络的预测方法通过利用神经网络的特征抽取和复杂系统建模能力，构建深度学习模型以表征设备的退化趋势，代表性的预测模型包括基于循环神经网络的数据预测模型[15]和基于长短期记忆网络（long short term memory，LSTM）的数据预测模型[16]等。基于相关向量机（relevance vector machine，RVM）的预测方法根据稀疏贝叶斯学习理论，通过约束隐变量分布可有效地对预测模型进行剪枝，从而提高预测模型的执行效率，降低对退化数据量的需求[17]。该类方法具有效率高、样本少、可提供概率化预测结果等优点，在设备剩余使用寿命预测中具有广泛的应用前景。
然而，在利用机器学习方法学习机械设备退化模型时，尽管可以获取大量的健康监测数据，但其中起关键作用的故障监测数据非常稀少。同时，快速的设备退化过程进一步加剧了有效数据的稀缺性。为了充分利用有限的故障监测数据，自适应地调整设备的状态预测模型，并提供具有置信度的数据预测能力，本文提出一种基于注意力机制的设备剩余使用寿命预测方法（attention-based remaining useful lifetime prediction，ARULP），通过在相关向量机的隐变量中引入局部注意力机制，并逐步更新注意力权重，从而更好地调整设备的状态预测模型，进一步提升设备的剩余使用寿命预测精度。基于西安交通大学滚动轴承加速寿命试验数据集的验证结果表明，所提出的设备剩余使用寿命预测方法（ARULP）在预测精度方面优于现有的其他同类预测方法。
1. 基于注意力的剩余寿命预测方法
基于注意力的设备剩余使用寿命预测方法包括模型训练阶段和模型预测阶段。在模型训练阶段，基于训练数据计算局部注意力度量并构建相应的设备状态预测模型。在模型预测阶段，利用前一阶段所构建的预测模型进行设备状态预测，进而计算设备的剩余使用寿命。
1.1 模型训练阶段
假设
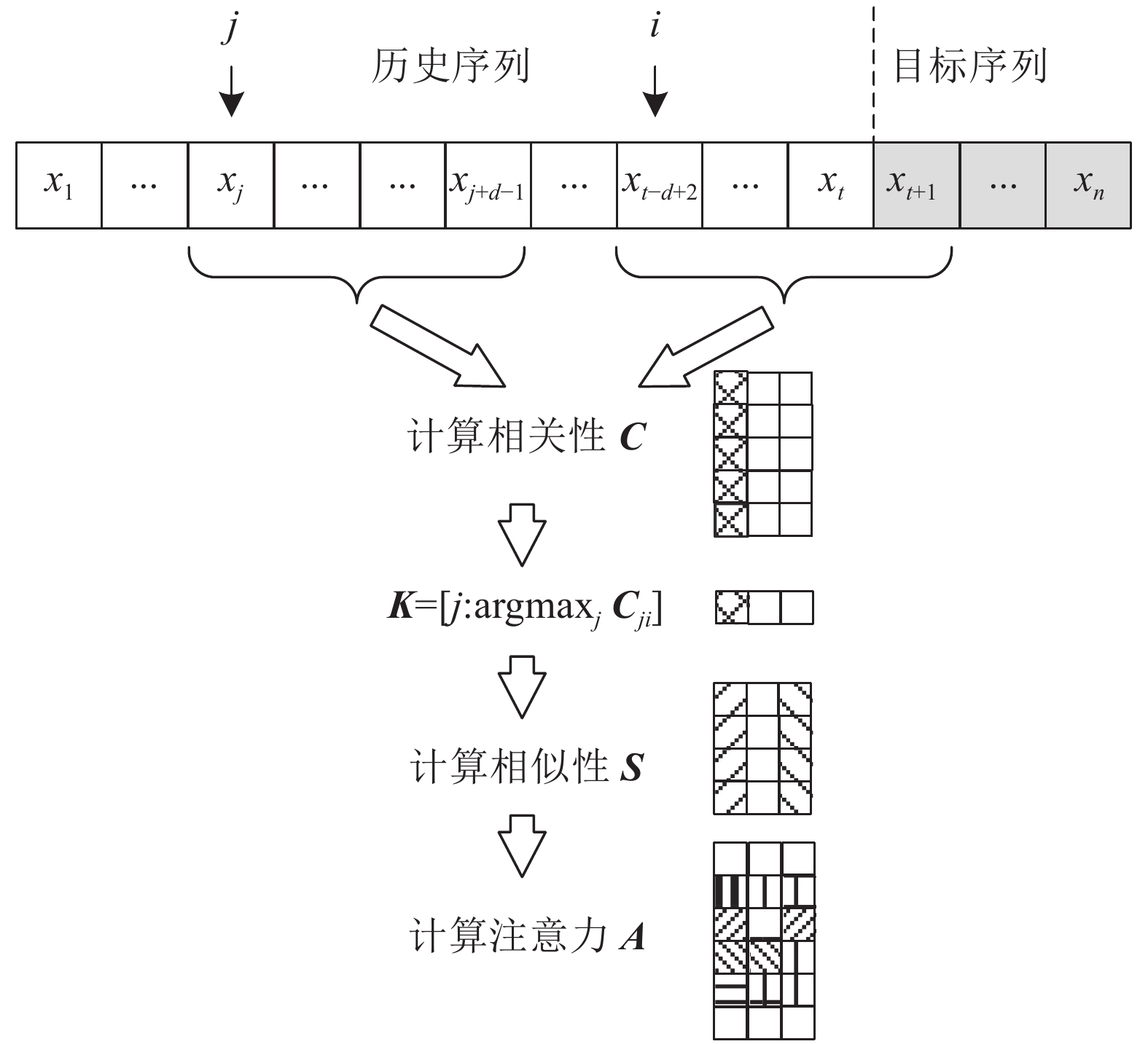
$ \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\} $ 为模型训练数据，其中，前t个数据$ \left\{ {{x_1},{x_2}, \cdots ,{x_t}} \right\} $ 被设置为历史序列，后n − t个数据$ \left\{ {{x_{t + 1}},{x_{t + 2}}, \cdots ,{x_n}} \right\} $ 被设置为目标序列。通过计算预测模型中隐变量的注意力度量，并学习预测模型参数，可基于历史序列对目标序列进行预测。目前，注意力机制已广泛应用于计算机视觉、自然语言处理、动作识别和推荐系统等应用领域[18-19]。该技术的核心思想是从输入序列中挑选少量与目标较为相关的主要信息，通过为其分配较大的权重，从而使模型重点关注大量数据中的关键信息，进而提高模型处理长序列数据的能力[20-21]。本文所设计的局部注意力计算模型如图1所示。
图 1 局部注意力计算模型Fig. 1 Local attention computation model
下载:
全尺寸图片
图1中，i和j分别为预测数据窗口和历史数据窗口的起始位置，d为窗口宽度。通过不断向前滑动历史数据窗口和预测数据窗口，可计算历史序列
$ \left\{ {{x_j},{x_{j + 1}}, \cdots ,{x_{j + d - 1}}} \right\} $ 和预测序列$ \left\{ {{x_i},{x_{i + 1}}, \cdots ,{x_{i + d - 1}}} \right\} $ 之间的相关性：$$\quad \;\;\;{C _{ji}} = \left\langle {\left\{ {{x_j},{x_{j + 1}}, \cdots ,{x_{j + d - 1}}} \right\},\left\{ {{x_i},{x_{i + 1}}, \cdots ,{x_{i + d - 1}}} \right\}} \right\rangle $$ (1) 假设
${\boldsymbol{K}} = \left[ {j:\arg {{\max }_j}{C _{ji}}} \right]$ 为相关性矩阵C中每列最大元素的索引所构成的行向量，则与预测数据序列$ \left\{ {{x_i},{x_{i + 1}}, \cdots ,{x_{i + d - 1}}} \right\} $ 最相关的历史序列为$\{ {x_k},{x_{k + 1}}, \cdots , {x_{k + d - 1}} \}$ ，其中$ k = {K_i} $ 。因此，两个数据序列间的相似性度量向量为：$$\;\;\;\;\;\;\;\;{{\boldsymbol{S}}_i} = {\left[ {\left| {{x_i} - {x_k}} \right|,\left| {{x_{i + 1}} - {x_{k + 1}}} \right|, \cdots ,\left| {{x_{i + d - 1}} - {x_{k + d - 1}}} \right|} \right]^{\text{T}}} $$ (2) 首先，将Si按列排列成相似性矩阵S；然后，利用sigmod函数将S逐列映射至[0,1]区间；最后，利用零填充将映射结果扩展至t行，即可获得所需的注意力度量矩阵A。综上所述，局部注意力计算算法如算法1所示。
算法1 局部注意力计算算法
输入：历史序列
$ \left\{ {{x_1},{x_2}, \cdots ,{x_t}} \right\} $ ，目标序列$\{{x_{t + 1}}, {x_{t + 2}}, \cdots ,{x_n} \}$ ；输出：注意力度量A；
1. For
$ i \in \left[ {t - d + 2,n - d + 1} \right] $ 2. For
$ j \in \left[ {1,i - 1} \right] $ 3. 利用式（1）计算
${C _{ji}}$ ；4.
${\boldsymbol{K}} = \left[ {j:\arg {{\max }_j}{C _{ji}}} \right]$ ；5. For
$ i \in [t - d + 2,n - d + 1] $ 6. 利用式（2）计算
$ {{\boldsymbol S}_i} $ ；7. A=extend(sigmoid(S))。
相关向量机基于稀疏贝叶斯学习理论，具有稀疏表征、核函数不受Mercer条件限制、可提供概率化的预测结果等优点[22]，其模型可表示为：
$$ y = \sum\limits_{i = 1}^t {{w_i}{\mathcal{K}}\left( {x,{x_i}} \right) + {w_0}} $$ (3) 式中：y为预测值；
$ w_0 $ 为偏置，$w_i（i=1,2,\cdots,t）$ 为模型参数，令${\boldsymbol{w}} = {\left[ {{w_0},{w_1}, \cdots ,{w_i}, \cdots ,{w_t}} \right]^{\text{T}}}$ 为模型参数向量；$ \mathcal{K}(\;) $ 为核函数。为方便描述，假设${\boldsymbol{\phi}} \left( x \right) = [ 1, \mathcal{K}\left( {x,{x_1}} \right),\mathcal{K}( x, {x_2}),\cdots , \mathcal{K}\left( {x,{x_t}} \right) ]$ 。因为$ {w_0} $ 服从均值为0、方差为$ \;{\beta ^{ - 1}} $ 的正态分布，即$ {w_0} \sim {\text{N}}\left( {0,{\beta ^{ - 1}}} \right) $ ，可知$y \sim {\text{N}}\left( {{\boldsymbol{\phi}} \left( x \right){\boldsymbol{w}},{\beta ^{ - 1}}} \right)$ 。因此，预测值y的条件概率分布为：$${\;\;\;\;\; p\left( {y\left| {{\boldsymbol{w}},{\beta ^{ - 1}}} \right.} \right){{ = }}\sqrt {\frac{1}{{2{\text{π}}{\beta ^{ - 1}}}}} \exp \left( {\frac{{{{\left( {y - {\boldsymbol{\phi}} \left( x \right){\boldsymbol{w}}} \right)}^2}}}{{{{ - }}2{\beta ^{ - 1}}}}} \right)} $$ (4) 如果采用最大似然法直接对式（4）进行求解，极易出现过拟合现象[23]。为避免此问题产生，通过稀疏贝叶斯学习理论为模型参数w定义了先验分布，即假设
$ {w_i} \sim {\text{N}}\left( {0,\alpha _i^{ - 1}} \right) $ 。故：$$ p\left( {{\boldsymbol{w}}\left| {\boldsymbol{\alpha}} \right.} \right) = \prod\limits_{i = 0}^t {{\rm N}\left( {{w_i}\left| {0,\alpha _i^{ - 1}} \right.} \right)} {{ = }} \prod\limits_{i = 0}^t {\sqrt {\frac{{{\alpha _i}}}{{{{2{\text{π}} }}}}} } \exp \left( { - \frac{{w_i^2{\alpha _i}}}{2}} \right) $$ (5) 式中，
${\boldsymbol{ \alpha }} = {\left[ {{\alpha _0},{\alpha _1}, \cdots ,{\alpha _t}} \right]^{\text{T}}} $ 为模型参数，其元素与参数w的元素一一对应。通过在参数${\boldsymbol{ \alpha }} $ 上增加注意力机制，可将式（5）改写为：$$ \begin{aligned}[b] p\left( {{\boldsymbol{w}}\left| {{\boldsymbol{c\alpha }}} \right.} \right) =& \prod\limits_{i = 0}^t {\sqrt {\frac{{{c_i}{\alpha _i}}}{{2{\text{π}}}}} } \exp \left( { - \frac{{w_i^2{c_i}{\alpha _i}}}{2}} \right){{ = }} \\& {\left( {{{2{\text{π}} }}} \right)^{ - \frac{{t + 1}}{2}}}{\left| {\boldsymbol{Z}} \right|^{\frac{1}{2}}}\exp \left( { - \frac{{{{\boldsymbol{w}}^{\text{T}}}{\boldsymbol{Z}}{\boldsymbol{w}}}}{2}} \right) \end{aligned} $$ (6) 式中，c为注意力度量矩阵A的相应列，Z=diag(
${{\boldsymbol{c\alpha }}} $ )为主对角线元素是${{\boldsymbol{c\alpha }}} $ 的对角阵。根据贝叶斯定理，由先验分布和似然估计，可得到参数w的后验分布为：
$$ \begin{aligned}[b] p\left( {{\boldsymbol{w}}\left| {t,{\boldsymbol{c\alpha}} ,{\beta ^{ - 1}}} \right.} \right) =& \frac{{p\left( {t\left| {{\boldsymbol{w}},{\beta ^{ - 1}}} \right.} \right)p\left( {{\boldsymbol{w}}\left| {{\boldsymbol{c\alpha}} } \right.} \right)}}{{p\left( {t\left| {{\boldsymbol{c\alpha}} ,{\beta ^{ - 1}}} \right.} \right)}}{{ = }} \\& {\left( {{{2{\text{π}} }}} \right)^{ - \frac{{t + 1}}{2}}}{\left| {\boldsymbol{\varSigma }} \right|^{{{ - }}\frac{1}{2}}}\exp \left( { - \frac{{{{\left( {{\boldsymbol{w}} - {\boldsymbol{\mu}} } \right)}^{\text{T}}}{{\boldsymbol{\varSigma}} ^{ - 1}}\left( {{\boldsymbol{w}} - {\boldsymbol{\mu }}} \right)}}{2}} \right) \end{aligned} $$ (7) 式中，
$\;{\boldsymbol{\mu}} = {{{\boldsymbol{\varSigma }} {\boldsymbol{\phi}} {{\left( x \right)}^{\text{T}}}y} /{{\beta ^{ - 1}}}}$ 为后验均值，${\boldsymbol{\varSigma}} = ( {\boldsymbol{Z }}+ {{\boldsymbol{\phi}} {{\left( x \right)}^{\text{T}}}{\boldsymbol{\phi }}\left( x \right)} / {{\;\beta ^{ - 1}}} )^{ - 1}$ 为后验方差。此时，预测值y的边缘概率密度函数可表示为：$$ \qquad \quad \;\;p( {y| {{\boldsymbol{c\alpha}} ,{\beta ^{ - 1}}} } ) = \int {p(y| {{\boldsymbol{w}},{\beta ^{ - 1}}} )p({\boldsymbol{w}}\left| {{\boldsymbol{c\alpha }}} \right.)} {\text{d}}{\boldsymbol{w}} $$ (8) 将式（4）和（6）代入式（8）后，对计算结果取对数可得：
$$ {\;\;\;\;\;\;\ln(p( {y| {{\boldsymbol{c\alpha}} ,{\beta ^{ - 1}}} } ) )= - \frac{1}{2}( {\left| \varOmega \right| + {\varOmega ^{ - 1}}{y^2}{{ + }}t\ln(2{\text{π}}}) )} $$ (9) 式中，
$ \varOmega {{ = }}{\beta ^{ - 1}} + {\boldsymbol{\phi }}\left( x \right){{\boldsymbol{Z}}^{ - 1}}{\boldsymbol{\phi}} {\left( x \right)^{\text{T}}} $ 。为求最优的预测模型参数
${\boldsymbol{\alpha}} $ 和$ \;{\beta ^{ - 1}} $ ，对式（9）分别求偏导可得：$$ \qquad \quad \;\; \frac{{\partial \ln (p( {y| {{\boldsymbol{c\alpha }},{\beta ^{ - 1}}} } ))}}{{\partial \ln ({\alpha _i})}} = \frac{1}{2}( {1 - {\alpha _i}( {\mu _i^2 + {\varSigma _{ii}}} )} ) $$ (10) $$ \begin{aligned}[b] \frac{{\partial \ln (p( {y| {{\boldsymbol{c\alpha}} ,{\beta ^{ - 1}}} } ))}}{{\partial \ln ({\beta ^{{{ - }}1}})}} =& \frac{t}{{2{\beta ^{{{ - }}1}}}}{{ - }}\frac{1}{2}{\left( {y - {\boldsymbol{\phi}} \left( x \right){\boldsymbol{\mu}} } \right)^2}{{ - }} \\& \frac{1}{2}{\text{tr}}( {{\boldsymbol{\varSigma \phi}} {{( x )}^{\text{T}}}{\boldsymbol{\phi}} \left( x \right)} ) \end{aligned} $$ (11) 令式（10）和（11）等于零，参数
${\boldsymbol{\alpha}} $ 和$\; {\beta ^{ - 1}} $ 的更新公式可表示为：$$ {\left( {{\alpha _i}} \right)^{\text{ + }}} = {{\left( {1{{ - }}{\alpha _i}{\varSigma _{ii}}} \right)} / {\mu _i^2}} $$ (12) $$ \qquad \qquad \qquad {( {{\beta ^{{{ - }}1}}} )^{\text{ + }}} = \frac{{{{\left( {y - {\boldsymbol{\phi}} \left( x \right){\boldsymbol{\mu }}} \right)}^2}}}{{n - t - \displaystyle\sum\limits_{i = 0}^t {\left( {1{{ - }}{\alpha _i}{\Sigma _{ii}}} \right)} }} $$ (13) 式中，
$ {\varSigma _{ii}} $ 为$ {\boldsymbol{\varSigma}} $ 的第i个对角线元素。综上所述，基于局部注意力的相关向量机算法如算法2所示。
算法2 基于局部注意力的相关向量机算法
输入：历史序列
$ \left\{ {{x_1},{x_2}, \cdots ,{x_t}} \right\} $ ，目标序列$\{ {x_{t + 1}}, {x_{t + 2}}, \cdots ,{x_n} \}$ ，最大迭代次数I，收敛误差ε；输出：模型参数
${\boldsymbol{\alpha }} $ 和$ \;{\beta ^{ - 1}} $ ；1. 初始化
${\boldsymbol{\alpha }} $ 为t+1维随机向量，$\; {\beta ^{ - 1}} $ 为[0,1]之间的随机标量；2. 利用算法1计算注意力度量A；
3. While 迭代次数小于I或
$ \left\| {{{\boldsymbol{\alpha}} ^{\text{ + }}}{{ - }}{\boldsymbol{\alpha }}} \right\| \ge \varepsilon $ ：4.
${\boldsymbol{\varSigma}} = {( {{\boldsymbol{Z}} + {{{\boldsymbol{\phi}} {{\left( x \right)}^{\text{T}}}{\boldsymbol{\phi}} \left( x \right)} / {{\beta ^{ - 1}}}}} )^{ - 1}}$ ；5.
$\;{\boldsymbol{\mu}} = {{{\boldsymbol{\varSigma \phi}} {{\left( x \right)}^{\text{T}}}y} / {{\beta ^{ - 1}}}}$ ；6.
${\left( {{\alpha _i}} \right)^{\text{ + }}} = {{\left( {1{{ - }}{\alpha _i}{\varSigma _{ii}}} \right)} / {\mu _i^2}}$ ；7.
${\left( {{\beta ^{{{ - }}1}}} \right)^{\text{ + }}} = \dfrac{{{{\left( {y - {\boldsymbol{\phi}} \left( {{x}} \right){\boldsymbol{\mu}} } \right)}^2}}}{{n - t - \displaystyle\sum\limits_{i = 0}^t {\left( {1{{ - }}{\alpha _i}{\varSigma _{ii}}} \right)} }}$ 。1.2 模型预测阶段
在模型预测阶段，对于新的退化数据
$ {x^*} $ ，其预测值$ {y^*} $ 服从均值为${\boldsymbol{\phi}} \left( {{x^*}} \right){\boldsymbol{\mu}}$ 、方差为$ \;{\beta ^{ - 1}} $ 的高斯分布，即${y^*} \sim {\text{N}}\left( {{\boldsymbol{\phi}} \left( {{x^*}} \right){\boldsymbol{\mu}} ,{\beta ^{ - 1}}} \right)$ ，因此预测结果为${y^*} = {\boldsymbol{\phi}} \left( {{x^*}} \right){\boldsymbol{\mu}}$ 。令${{\textit{z}}_{{\theta \mathord{\left/ {\vphantom {\theta}} \right. } 2}}}$ 为置信水平为1 − θ的分位点，$ {\tau _{\rm L}} $ 和$ {\tau _{\rm U}} $ 分别为相应的置信下限和置信上限，具体表示如下：$$ {\tau _{\rm L}} = {y^*} - \sqrt {{{\left( {{\beta ^{ - 1}}} \right)}^*}} {{\textit{z}}_{{\theta / 2}}} $$ (14) $$ {\tau _{\rm U}} = {y^*} + \sqrt {{{\left( {{\beta ^{ - 1}}} \right)}^*}} {{\textit{z}}_{{\theta / 2}}} $$ (15) 式中，
${\left( {{\beta ^{ - 1}}} \right)^*} = {\beta ^{ - 1}} + {\boldsymbol{\phi}} \left( {{x^*}} \right){\boldsymbol{\varSigma \phi }}{\left( {{x^*}} \right)^{\text{T}}}$ 。当预测结果超过设备的合理阈值范围$ \left[ {{\tau _{\rm L}},{\tau _{\rm U}}} \right] $ 时，即判定该设备丧失设计的运行能力，所经历的时间即为ARULP方法所预测的设备剩余使用寿命。2. 实验分析
为了分析ARULP方法的有效性，本文采用西安交通大学滚动轴承加速寿命试验数据集（XJTU–SY数据集）[24]进行验证。该数据集使用轴承加速退化测试平台对型号为LDK UER204的滚动轴承进行性能退化实验，其中包含了轴承的全寿命周期振动数据，收集工况分别为：工况1，频率35 Hz，径向力12 kN；工况2，频率37.5 Hz，径向力11 kN；工况3，频率40 Hz，径向力10 kN；测试轴承的失效部件涵盖了轴承的外圈、内圈、保持架等失效位置。典型的失效轴承类型包括轴承的内圈磨损、保持架断裂、外圈磨损、外圈断裂[25]，具体情况如图2所示。
图 2 轴承的失效类型Fig. 2 Types of bearing failure下载:
全尺寸图片
XJTU–SY数据集中不同测试轴承的失效位置如表1所示。
表 1 测试轴承的失效位置Table 1 Failure positions of test bearings工
况轴承
1轴承
2轴承
3轴承
4轴承
51 外圈 外圈 外圈 保持架 内外圈 2 内圈 外圈 保持架 外圈 外圈 3 外圈 内外圈
保持架内圈 内圈 外圈 实验过程中所对比分析的方法包括：
1）相关向量机RVM。该方法基于稀疏贝叶斯学习理论，利用独立先验分布参数构建预测模型，可提供带置信区间的预测结果。
2）自回归模型AR。该方法利用历史退化数据构建具有随机误差的线性方程，从而表示设备退化状态的回归模型，并根据模型中的回归系数预测系统的状态。
3）自回归移动平均模型ARIMA。该方法包括自回归模型、移动平均模型和差分算子3个子部分，可处理非平稳时间序列数据，构建复杂回归模型并进行状态预测。
4）长短期记忆网络LSTM。该方法利用深度学习的特征抽象和表征能力，结合特殊门限设置可实现长序列数据的学习能力，从而实现对设备的未来状态预测。
实验中的性能度量指标采用相对均方误差（relative mean square error, RMSE）和平均绝对误差（mean absolute error，MAE），其定义分别为：
$$ \qquad \qquad \qquad {\gamma _{{\text{RMSE}}}} = \sqrt {{{\sum\limits_{i = 1}^m {{{({y_i} - y_{_i}^*)}^2}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^m {{{({y_i} - y_{_i}^*)}^2}} } m}} \right. } m}} $$ (16) $$ {\gamma _{{\text{MAE}}}} = {{\sum\limits_{i = 1}^m {|{y_i} - y_i^*|} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^m {|{y_i} - y_i^*|} } m}} \right. } m} $$ (17) 式中，
$ {y_i} $ 和$ y_i^* $ 分别为真实数据和预测数据，m为预测数据量。实验过程中，将训练数据集与测试数据集按照7∶3的比例进行划分，历史序列长度t设置为训练数据集长度的1/4，注意力窗口宽度d设置为0.1t，置信水平设置为95%，核函数采用高斯核，故障阈值设置为实验对象正常工作时最大幅值的10倍。表2和3分别给出了ARULP方法与基准方法在3组不同工况下针对具有不同失效位置的轴承进行预测时的RMSE和MAE结果。由表2和3可知，由于ARULP方法融入了注意力机制，使其具有更高的预测精度，在不同工况和不同故障时其表现都是最优的。
表 2 不同预测方法对轴承振动数据预测的RMSE对比Table 2 Comparison of RMSE for bearing vibration prediction by different methods工
况方
法轴承1 轴承2 轴承3 轴承4 轴承5 1 RVM 0.136 0.295 0.083 0.178 0.230 AR 0.202 0.482 0.223 0.166 0.432 ARIMA 0.151 0.109 0.061 0.153 0.120 LSTM 0.082 0.106 0.071 0.178 0.146 ARULP 0.079 0.069 0.058 0.073 0.043 2 RVM 0.077 0.057 0.043 0.131 0.068 AR 0.364 0.089 0.106 0.184 0.205 ARIMA 0.085 0.037 0.033 0.115 0.094 LSTM 0.198 0.040 0.043 0.159 0.083 ARULP 0.065 0.036 0.025 0.090 0.051 3 RVM 0.069 0.263 0.167 0.138 0.031 AR 0.191 0.292 0.560 0.427 0.384 ARIMA 0.078 0.158 0.070 0.148 0.035 LSTM 0.072 0.168 0.072 0.228 0.143 ARULP 0.066 0.127 0.062 0.122 0.026 表 3 不同预测方法对轴承振动数据预测的MAE对比Table 3 Comparison of MAE for bearing vibration prediction by different methods工
况方
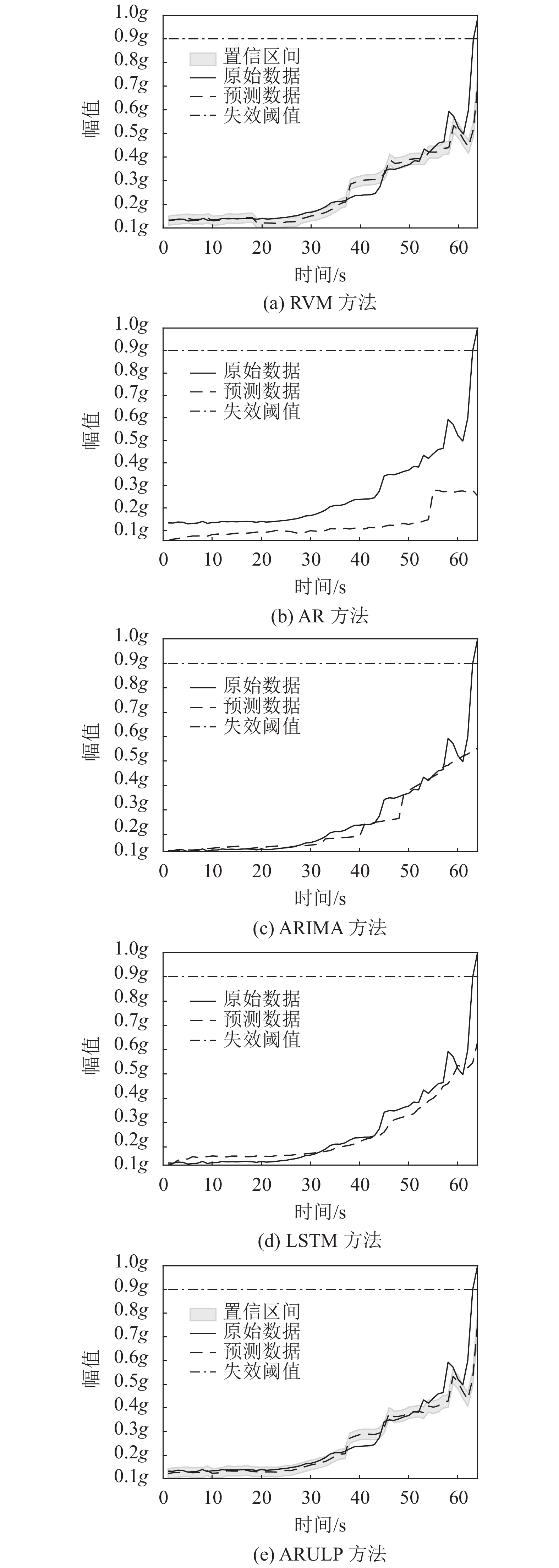
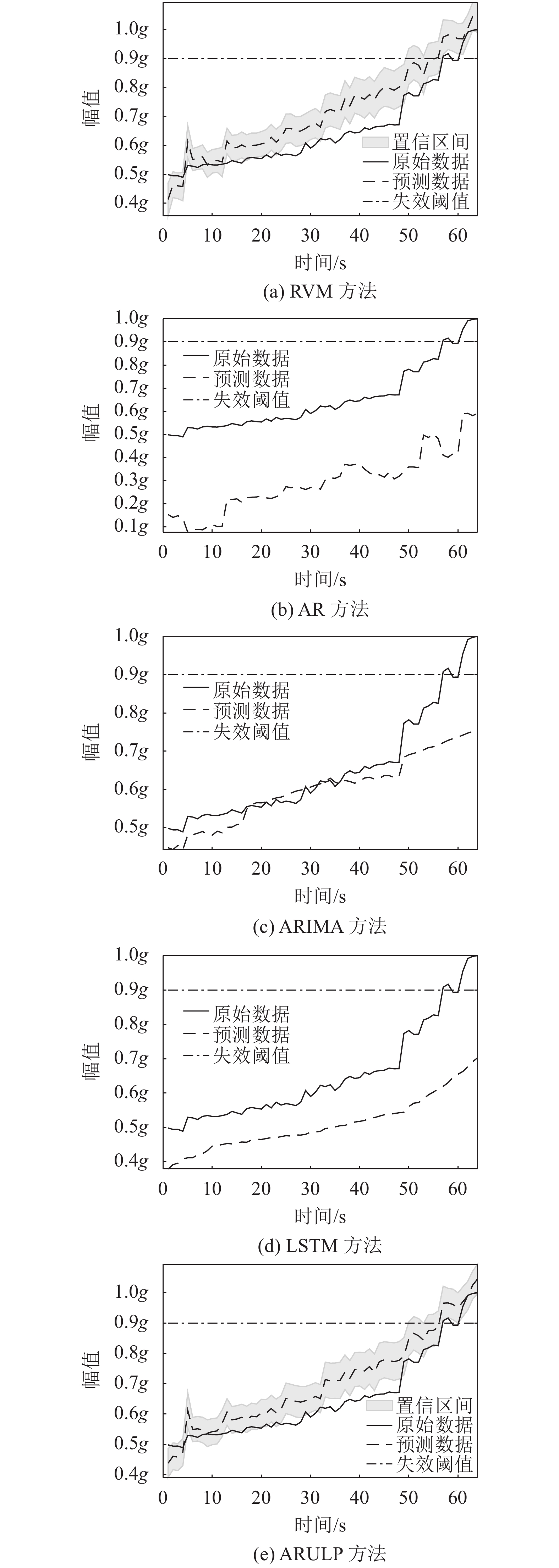
法轴承1 轴承2 轴承3 轴承4 轴承5 1 RVM 0.077 0.273 0.067 0.065 0.185 AR 0.109 0.475 0.220 0.060 0.396 ARIMA 0.072 0.081 0.053 0.064 0.080 LSTM 0.039 0.079 0.061 0.034 0.091 ARULP 0.037 0.051 0.046 0.026 0.028 2 RVM 0.068 0.051 0.036 0.115 0.055 AR 0.359 0.078 0.098 0.148 0.182 ARIMA 0.057 0.032 0.027 0.080 0.063 LSTM 0.170 0.032 0.031 0.139 0.060 ARULP 0.057 0.030 0.019 0.062 0.042 3 RVM 0.033 0.204 0.143 0.116 0.023 AR 0.141 0.228 0.548 0.347 0.375 ARIMA 0.032 0.124 0.046 0.123 0.026 LSTM 0.036 0.137 0.059 0.205 0.140 ARULP 0.030 0.101 0.056 0.101 0.020 为了衡量不同预测方法针对不同类型的故障进行预测时的实际性能，针对轴承外圈故障、轴承内圈故障和轴承保持架故障使用上述5种预测方法进行了预测，其具体结果对比如图3～5所示。
图 3 轴承外圈故障不同方法预测结果对比Fig. 3 Comparison of outer ring fault prediction results by different methods下载:
全尺寸图片
图 4 轴承内圈故障不同方法预测结果对比Fig. 4 Comparison of inner ring fault prediction results by different methods下载:
全尺寸图片
图 5 轴承保持架故障不同方法预测结果对比Fig. 5 Comparison of cage fault prediction results by different methods下载:
全尺寸图片
从图3中可以看出：在轴承外圈故障预测时，本文所提出的ARULP方法的预测结果与轴承实际退化数据最为接近，能够较好地反映故障轴承的退化状态。相比之下，RVM方法的预测误差略高于ARULP方法；AR方法和ARIMA方法只能在一定程度上反映轴承的退化趋势；LSTM方法在预测过程中预测曲线过于平稳，因此会丢失较多的细节信息。
从图4中可以看出：轴承内圈故障的振幅曲线比轴承外圈故障抖动得更加剧烈，因此在该类故障下进行数据预测时更加困难。在该故障下，ARULP方法的预测结果更加贴近实际数据。相比之下，RVM方法的预测结果稍逊于ARULP方法；AR方法在此故障模式下具有较差的预测结果，预测误差间隔较大；ARIMA方法和LSTM方法的预测曲线较为平缓，无法反映细节预测信息，最终的剩余寿命预测结果和实际情况出入较大。
从图5中可以看出：轴承保持架故障发生时，实际退化数据的曲线振幅抖动情况最为剧烈。本文所提出的ARULP方法在该故障模式下依然具有明显的预测精度优势。相比之下，RVM方法和AR方法的预测结果与轴承实际退化数据的差距较大，ARIMA方法和LSTM方法的预测细节丢失情况依旧显著。
3. 结 论
针对如何预测工业物联网中的设备剩余使用寿命问题进行研究，采用局部注意力机制和相关向量机，提出一种有效的设备剩余使用寿命预测方法。通过分别设计局部注意力计算算法和基于局部注意力的相关向量机，并将局部注意力机制有效融入设备的状态预测模型，使其能对预测模型中的参数自适应学习，从而实现对设备剩余使用寿命高精度预测。通过与多种基准方法在XJTU–SY数据集上进行对比实验，表明了所提方法的有效性。下一步研究方向将重点考虑如何提高设备剩余使用寿命预测方法的效率。
-
图 1 局部注意力计算模型
Fig. 1 Local attention computation model
下载:
全尺寸图片
图 2 轴承的失效类型
Fig. 2 Types of bearing failure
下载:
全尺寸图片
图 3 轴承外圈故障不同方法预测结果对比
Fig. 3 Comparison of outer ring fault prediction results by different methods
下载:
全尺寸图片
图 4 轴承内圈故障不同方法预测结果对比
Fig. 4 Comparison of inner ring fault prediction results by different methods
下载:
全尺寸图片
图 5 轴承保持架故障不同方法预测结果对比
Fig. 5 Comparison of cage fault prediction results by different methods
下载:
全尺寸图片
表 1 测试轴承的失效位置
Table 1 Failure positions of test bearings
工
况轴承
1轴承
2轴承
3轴承
4轴承
51 外圈 外圈 外圈 保持架 内外圈 2 内圈 外圈 保持架 外圈 外圈 3 外圈 内外圈
保持架内圈 内圈 外圈 表 2 不同预测方法对轴承振动数据预测的RMSE对比
Table 2 Comparison of RMSE for bearing vibration prediction by different methods
工
况方
法轴承1 轴承2 轴承3 轴承4 轴承5 1 RVM 0.136 0.295 0.083 0.178 0.230 AR 0.202 0.482 0.223 0.166 0.432 ARIMA 0.151 0.109 0.061 0.153 0.120 LSTM 0.082 0.106 0.071 0.178 0.146 ARULP 0.079 0.069 0.058 0.073 0.043 2 RVM 0.077 0.057 0.043 0.131 0.068 AR 0.364 0.089 0.106 0.184 0.205 ARIMA 0.085 0.037 0.033 0.115 0.094 LSTM 0.198 0.040 0.043 0.159 0.083 ARULP 0.065 0.036 0.025 0.090 0.051 3 RVM 0.069 0.263 0.167 0.138 0.031 AR 0.191 0.292 0.560 0.427 0.384 ARIMA 0.078 0.158 0.070 0.148 0.035 LSTM 0.072 0.168 0.072 0.228 0.143 ARULP 0.066 0.127 0.062 0.122 0.026 表 3 不同预测方法对轴承振动数据预测的MAE对比
Table 3 Comparison of MAE for bearing vibration prediction by different methods
工
况方
法轴承1 轴承2 轴承3 轴承4 轴承5 1 RVM 0.077 0.273 0.067 0.065 0.185 AR 0.109 0.475 0.220 0.060 0.396 ARIMA 0.072 0.081 0.053 0.064 0.080 LSTM 0.039 0.079 0.061 0.034 0.091 ARULP 0.037 0.051 0.046 0.026 0.028 2 RVM 0.068 0.051 0.036 0.115 0.055 AR 0.359 0.078 0.098 0.148 0.182 ARIMA 0.057 0.032 0.027 0.080 0.063 LSTM 0.170 0.032 0.031 0.139 0.060 ARULP 0.057 0.030 0.019 0.062 0.042 3 RVM 0.033 0.204 0.143 0.116 0.023 AR 0.141 0.228 0.548 0.347 0.375 ARIMA 0.032 0.124 0.046 0.123 0.026 LSTM 0.036 0.137 0.059 0.205 0.140 ARULP 0.030 0.101 0.056 0.101 0.020 -
[1] Qin Wei,Chen Siqi,Peng Mugen.Recent advances in Industrial Internet:Insights and challenges[J].Digital Communications and Networks,2020,6(1):1–13. doi: 10.1016/j.dcan.2019.07.001 [2] Sisinni E,Saifullah A,Han Song,et al.Industrial Internet of Things:Challenges,opportunities,and directions[J].IEEE Transactions on Industrial Informatics,2018,14(11):4724–4734. doi: 10.1109/TII.2018.2852491 [3] Zhang Liangwei,Lin Jing,Liu Bin,et al.A review on deep learning applications in prognostics and health management[J].IEEE Access,2019,7:162415–162438. doi: 10.1109/ACCESS.2019.2950985 [4] 雷亚国,贾峰,孔德同,等.大数据下机械智能故障诊断的机遇与挑战[J].机械工程学报,2018,54(5):94–104. doi: 10.3901/JME.2018.05.094 Lei Yaguo,Jia Feng,Kong Detong,et al.Opportunities and challenges of machinery intelligent fault diagnosis in big data era[J].Journal of Mechanical Engineering,2018,54(5):94–104 doi: 10.3901/JME.2018.05.094 [5] Li Xiang,Zhang Wei,Ding Qian.Cross-domain fault diagnosis of rolling element bearings using deep generative neural networks[J].IEEE Transactions on Industrial Electronics,2019,66(7):5525–5534. doi: 10.1109/TIE.2018.2868023 [6] Gou Bin,Xu Yan,Feng Xue.State-of-health estimation and remaining-useful-life prediction for lithium-ion battery using a hybrid data-driven method[J].IEEE Transactions on Vehicular Technology,2020,69(10):10854–10867. doi: 10.1109/TVT.2020.3014932 [7] Li Hong,Pan Donghui,Chen C L P.Reliability modeling and life estimation using an expectation maximization based Wiener degradation model for momentum wheels[J].IEEE Transactions on Cybernetics,2015,45(5):955–963. doi: 10.1109/TCYB.2014.2341113 [8] Hu Jiawen,Sun Qiuzhuang,Ye Zhisheng,et al.Joint modeling of degradation and lifetime data for RUL prediction of deteriorating products[J].IEEE Transactions on Industrial Informatics,2021,17(7):4521–4531. doi: 10.1109/TII.2020.3021054 [9] Lei Yaguo,Li Naipeng,Guo Liang,et al.Machinery health prognostics:A systematic review from data acquisition to RUL prediction[J].Mechanical Systems and Signal Processing,2018,104:799–834. doi: 10.1016/j.ymssp.2017.11.016 [10] Xia Tangbin,Dong Yifan,Xiao Lei,et al.Recent advances in prognostics and health management for advanced manufacturing paradigms[J].Reliability Engineering & System Safety,2018,178:255–268. doi: 10.1016/j.ress.2018.06.021 [11] Sun Bo,Li Yu,Wang Zili,et al.An improved inverse Gaussian process with random effects and measurement errors for RUL prediction of hydraulic piston pump[J].Measurement,2021,173:108604. doi: 10.1016/j.measurement.2020.108604 [12] 金晓航,李建华,郭远晶,等.基于二元混合随机过程的轴承剩余寿命预测[J].高技术通讯,2020,30(12):1284–1291. doi: 10.3772/j.issn.1002-0470.2020.12.009 Jin Xiaohang,Li Jianhua,Guo Yuanjing,et al.Binary hybrid stochastic process-based approach for the estimation of bearing remaining useful life[J].Chinese High Technology Letters,2020,30(12):1284–1291 doi: 10.3772/j.issn.1002-0470.2020.12.009 [13] Barraza–Barraza D,Tercero–Gómez V G,Beruvides M G,et al.An adaptive ARX model to estimate the RUL of aluminum plates based on its crack growth[J].Mechanical Systems and Signal Processing,2017,82:519–536. doi: 10.1016/j.ymssp.2016.05.041 [14] Li Xiaoyu,Yuan Changgui,Wang Zhenpo.Multi-time-scale framework for prognostic health condition of lithium battery using modified Gaussian process regression and nonlinear regression[J].Journal of Power Sources,2020,467:228358. doi: 10.1016/j.jpowsour.2020.228358 [15] Yu Wennian,Kim I Y,Mechefske C.Analysis of different RNN autoencoder variants for time series classification and machine prognostics[J].Mechanical Systems and Signal Processing,2021,149:107322. doi: 10.1016/j.ymssp.2020.107322 [16] Wu Jiyan,Wu Min,Chen Zhenghua,et al.Degradation-aware remaining useful life prediction with LSTM autoencoder[J].IEEE Transactions on Instrumentation and Measurement,2021,70:1–10. doi: 10.1109/TIM.2021.3055788 [17] Wang Xiuli,Jiang Bin,Lu Ningyun.Adaptive relevant vector machine based RUL prediction under uncertain conditions[J].ISA Transactions,2019,87:217–224. doi: 10.1016/j.isatra.2018.11.024 [18] 王文冠,沈建冰,贾云得.视觉注意力检测综述[J].软件学报,2019,30(2):416–439. doi: 10.13328/j.cnki.jos.005636 Wang Wenguan,Shen Jianbing,Jia Yunde.Review of visual attention detection[J].Journal of Software,2019,30(2):416–439 doi: 10.13328/j.cnki.jos.005636 [19] 柴玉梅,员武莲,王黎明,等.基于双注意力机制和迁移学习的跨领域推荐模型[J].计算机学报,2020,43(10):1924–1942. doi: 10.11897/SP.J.1016.2020.01924 Chai Yumei,Yun Wulian,Wang Liming,et al.A cross-domain recommendation model based on dual attention mechanism and transfer learning[J].Chinese Journal of Computers,2020,43(10):1924–1942 doi: 10.11897/SP.J.1016.2020.01924 [20] 杜柳青,李仁杰,李宝钏.基于注意力机制的数控机床热误差深度学习预测方法[J].工程科学与技术,2021,53(6):194–203. doi: 10.15961/j.jsuese.202100340 Du Liuqing,Li Renjie,Li Baochuan.Deep learning prediction for thermal error of CNC machine tools based on attention mechanism[J].Advanced Engineering Sciences,2021,53(6):194–203 doi: 10.15961/j.jsuese.202100340 [21] Niu Zhaoyang,Zhong Guoqiang,Yu Hui.A review on the attention mechanism of deep learning[J].Neurocomputing,2021,452:48–62. doi: 10.1016/j.neucom.2021.03.091 [22] Tipping M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001,1:211–244. doi: 10.1162/15324430152748236 [23] Jia Shun,Ma Bo,Guo Wei,et al.A sample entropy based prognostics method for lithium-ion batteries using relevance vector machine[J].Journal of Manufacturing Systems,2021,61:773–781. doi: 10.1016/j.jmsy.2021.03.019 [24] Wang Biao,Lei Yaguo,Li Naipeng,et al.A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[J].IEEE Transactions on Reliability,2020,69(1):401–412. doi: 10.1109/TR.2018.2882682 [25] 雷亚国,韩天宇,王彪,等.XJTU–SY滚动轴承加速寿命试验数据集解读[J].机械工程学报,2019,55(16):1–6. doi: 10.3901/JME.2019.16.001 Lei Yaguo,Han Tianyu,Wang Biao,et al.XJTU–SY rolling element bearing accelerated life test datasets:A tutorial[J].Journal of Mechanical Engineering,2019,55(16):1–6 doi: 10.3901/JME.2019.16.001
