GNSS Navigation Spoofing Method of UAV Based on Point-by-point Offset
-
摘要: 针对无人机在失控肇事、干扰航管等方面的危害，本文提出一种基于逐点拉偏式卫星导航欺骗方法，通过重构错误的导航坐标系诱骗目标无人机飞离敏感区域保护地面安全。该方法将整个无人机欺骗过程看作是单步位置欺骗拉偏的时间迭代过程，首先，根据无人机的运动学模型以及外部量测信息估算出无人机的真实位置点以及真实控制输入量；然后，考虑无人机飞行控制器对欺骗效果的影响，在真实控制输入量中抵消掉预先设置的欺骗控制力矩效果，设计构造虚假卫星信号使得GNSS/INS组合导航模式下的滤波估计无人机位置点仍靠近原始期望目标点，但发生了偏差；最后，这种偏差产生的无人机轨迹跟踪控制输入量会导致无人机真实状态点往欺骗目标点偏移，实现单步卫星导航欺骗效果。单步欺骗过程在时间上的迭代运用，可实现无人机位置的逐点偏移式欺骗。仿真结果表明，利用逐点偏移式卫星导航欺骗方法能使得目标无人机慢慢偏离原始轨迹而跟踪欺骗轨迹，且组合导航滤波器估计轨迹仍跟踪原始参考轨迹，达到了卫星导航欺骗的目的。本文提出的基于逐点拉偏式卫星导航欺骗干扰技术可用于保障重点区域/人员的低空安全防护。
-
关键词:
- 无人机 /
- 单步位置偏移 /
- 逐点偏移 /
- 卫星导航欺骗 /
- GNSS/INS组合导航
Abstract: Aiming at the harm of UAVs in the aspects of out-of-control accident and air traffic control interference, a GNSS navigation spoofing method based on point-by-point offset was proposed in this paper, which decoys target UAV to fly away from sensitive areas and protect ground security by reconstructing the wrong navigation coordinate system. It regards the entire UAV spoofing course as time-iterative process of one-step position spoofing bias. Firstly, the actual positions and actual control inputs were estimated according to the kinematica model of UAV and external measurement information; then, the pre-set fraudulent control effects were cancelled out from the actual control inputs, and the deceptive GNSS signals were designed and constructed so that the filter position estimates in GNSS/INS integrated navigation mode were still close to the original expected point, but had the offset; finally, the real state point of UAV was moved to the spoofed target point caused by the trajectory tracking control inputs generated by the offset , thereby achieving a one-step covert spoofing effect. Finally, the point-by-point position offset spoofing of UAV was completed by the iterative application of the one-step spoofing process over time. Simulation results verified the effectiveness of the proposed GNSS navigation spoofing method of UAV. The simulation results showed that the target UAV can slowly deviate from the original trajectory and track the deceptive trajectory by using the GNSS navigation spoofing method based on point-by-point offset, and the trajectory estimated by the integrated navigation filter still tracks the original reference trajectory, thus achieving the purpose of satellite navigation deception. The proposed spoof jamming technique based on point-by-point pull-biased satellite navigation can be used to protect key areas/personnel at low altitude. -
随着科学技术的快速进步和社会经济的蓬勃发展，以往披着神秘面纱的无人机如今已经进入民用市场[1-2]。由于无人机在尺寸速度[3]、机动性[4]及降低生命危险[5]等方面具有独特的优势，因此其适用范围已从警用执法、电力巡检、地质勘探、环境监测，向农业植保、快递送货、影视航拍等诸多领域迅速拓展[6]。
全球定位系统（global navigation satellite system, GNSS）/惯性导航系统（inertial navigation system，INS）的组合导航方法是无人机平台导航、制导与控制的核心技术之一[7-8]。由于导航卫星离地面20 000～36 000 km，卫星信号非常微弱，故GNSS导航终端容易受到压制式干扰和欺骗式干扰等恶意干扰[9-10]。由于欺骗式干扰是针对卫星导航系统的工作原理、卫星接收机工作特性以及存在薄弱环节采用更为隐蔽的方式进行干扰，因此欺骗式干扰的效果要明显优于压制式干扰[11]。以采用GNSS/INS组合导航技术的各类无人机作为攻击目标，利用欺骗式干扰对其实施精确位置偏移（以便捕获或打击），这在实际应用中是十分有必要的[12-13]。
目前，民用卫星信号的结构公开已知，针对民用卫星信号的欺骗式干扰是完全可以实现的，特别是伊朗连续两年成功捕获 “RQ–170”[14-15]和“扫描鹰”无人机[16-17]实例充分验证了卫星欺骗式干扰的可行性。越来越多的研究机构开始利用GNSS欺骗设备对依赖GNSS进行导航的终端开展欺骗测试实验。2008年Humphreys成功自制第一台真正意义上的便携式欺骗干扰机[18]，并在2012年通过释放欺骗干扰信号改变一架小型无人机的飞行路径；同年6月，Humphreys再次成功测试欺骗干扰机控制民用无人机的能力[19-20]；紧接着， Humphreys又成功地让一艘超级游艇在船长毫不知情的情况下使其偏离航向[21-22]。
Su[23]等描述了一种利用GPS欺骗攻击将装备有故障检测器的无人机驱动到任意目标地的场景，通过将整个欺骗攻击模型转化为约束优化问题，来量化每个时刻对GPS攻击下的无人机最大可达位置集。张会锁等[24]提出了一种利用轨迹诱导的欺骗式干扰方法，通过在每颗卫星上施加不同的传播时延和多普勒控制量来实现位置和速度同时欺骗，但是其欺骗方法只针对纯卫星导航终端，对于GNSS/INS组合导航终端实施可行性需要进一步验证。王文益[25]、李畅[26]等虽然设计了一套在INS/GNSS组合导航模式下诱捕无人机的完整步骤，但是整个诱捕过程中并没有考虑无人机飞行控制器对卫星导航欺骗的影响，无人机飞行控制器会产生控制指令来迫使无人机始终跟踪原定的参考轨迹/期望终止点，这与欺骗的目标是相违背的。
针对此，本文首先分析单步实施无人机位置欺骗的方法，即首先模拟无人机的运动学模型，利用外部传感器估算出无人机的真实飞行状态信息和控制输入量；然后为抵消无人机飞行控制器对卫星导航欺骗的影响，在真实控制输入量中减去欺骗控制效果求取虚假GNSS信号的加速度分量，积分计算获得虚假GNSS信号并施加到无人机系统中；GNSS/INS滤波数据融合之后产生错误的估计状态，进而得到错误的系统控制输入量；最后加入到无人机控制系统中，迫使无人机的真实位置点往欺骗目标点位置偏移，而远离原始期望目标点。在每个GNSS信号接收时间点上，循环迭代实施该单步欺骗过程即构成了整体的无人机欺骗方案，即基于逐点偏移式卫星导航欺骗方案。最后，根据虚假GNSS信号的设计构造原理，分析该卫星导航欺骗方案的有效性。通过实验验证该卫星导航欺骗方案能使得无人机始终跟踪欺骗轨迹，而其自身GNSS/INS组合导航滤波器输出的估计状态仍然绕着原始期望轨迹运行，达到了无人机欺骗效果。
1. 无人机导航与控制闭环模型构建
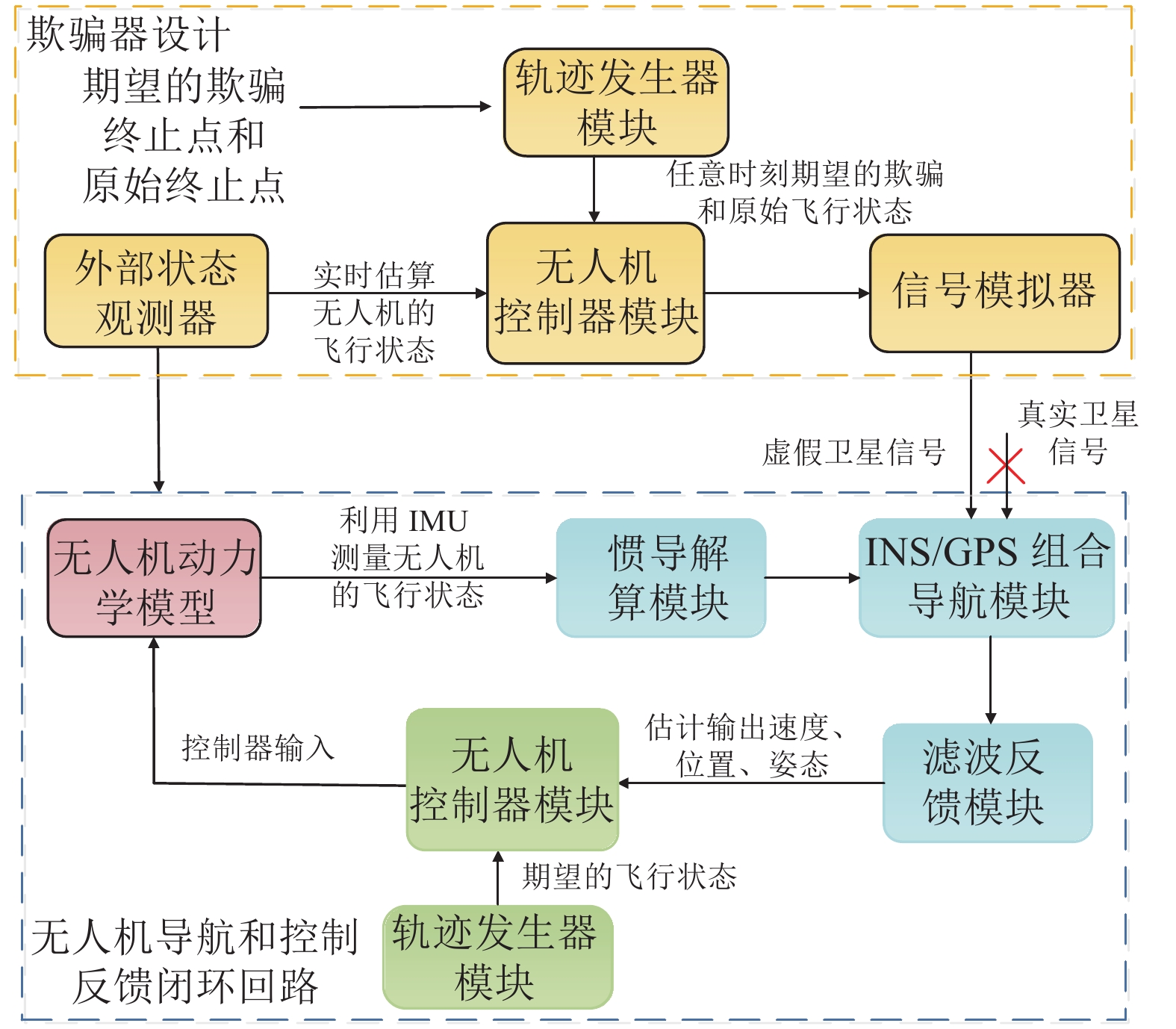
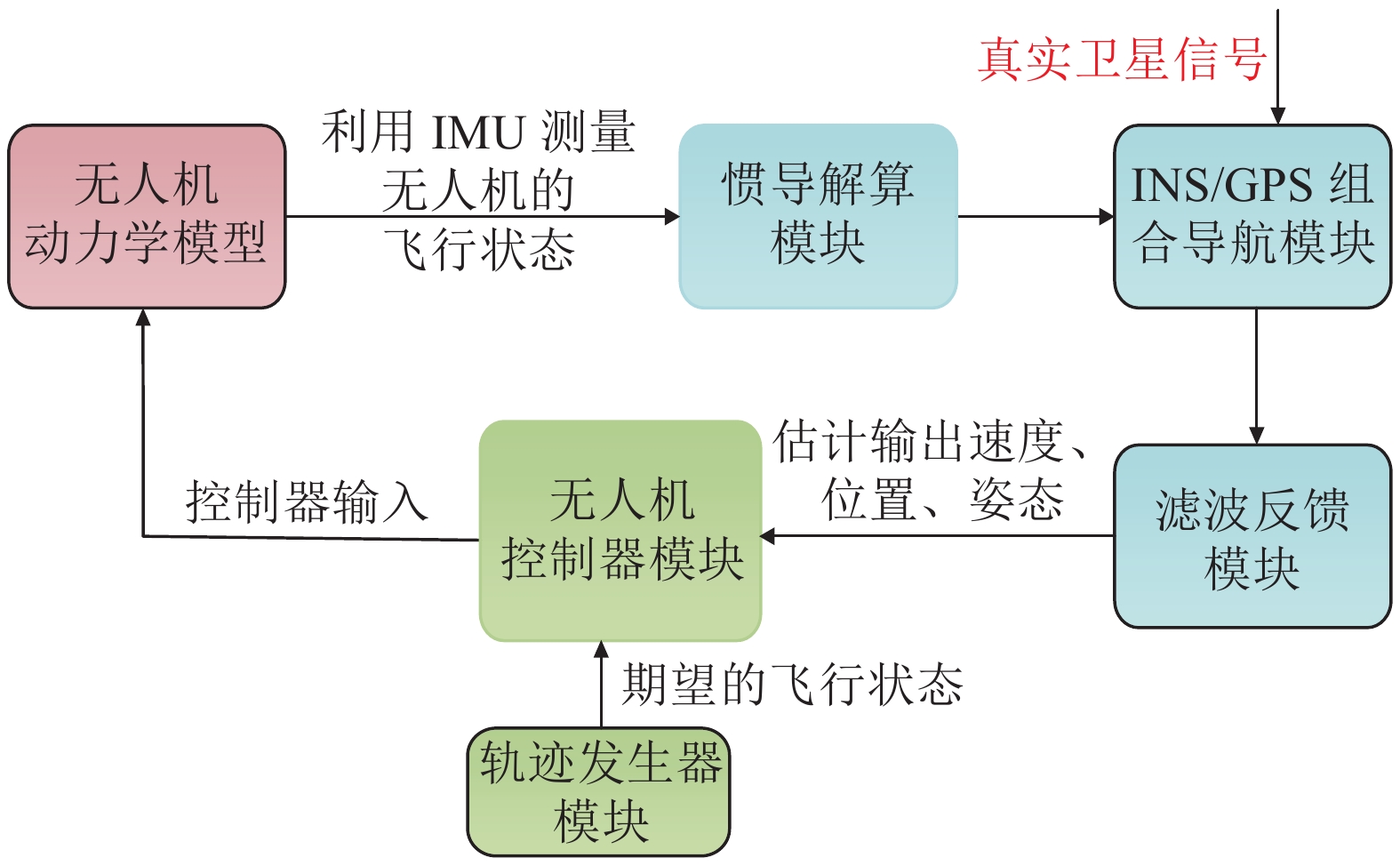
图1给出无人机导航和控制反馈闭环回路。从图1可以看出：GNSS/INS组合导航系统是无人机飞行控制回路的测量单元，其输出的飞行状态信息用于无人机飞行轨迹跟踪控制；同时，无人机飞行控制量作用到执行器件中会导致其飞行状态的变化，继而导致组合导航输出结果的改变。因此，认知无人机导航与控制闭环模型是研究针对其欺骗算法的前提。
图 1 无人机导航和控制反馈闭环回路图Fig. 1 Diagram of UAV navigation and control feedback closed loop
下载:
全尺寸图片
对于GNSS/INS组合导航系统，选取无人机位置信息和速度信息为状态变量，即
${{\boldsymbol{X}}_k} = [ {r_{x,k}},{r_{y,k}},{r_{{\textit{z}},k}},{v_{x,k}},{v_{y,k}}, {v_{{\textit{z}},k}} ]^{\rm{T}}$ ，则无人机的运动学模型一般形式为：$$ {{\boldsymbol{X}}_k} = {\boldsymbol{\varPhi}} {{\boldsymbol{X}}_{k - 1}} + {\boldsymbol{\varGamma}} {{\boldsymbol{a}}_{k - 1}} $$ (1) 式中：
${{\boldsymbol{a}}_{k - 1}}$ 为无人机的加速度信息，且${{\boldsymbol{a}}_{k - 1}} = [ {{a_{x,k - 1}}} {{a_{y,k - 1}}}\quad {{a_{{\textit{z}},k - 1}}} ]^{\rm{T}}$ ；${\boldsymbol{\varPhi}}$ 和${\boldsymbol{\varGamma}}$ 分别为无人机运动学模型的一步转移矩阵和系统噪声驱动矩阵，且$$ {\boldsymbol{\varPhi}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&T&0&0 \\ 0&1&0&0&T&0 \\ 0&0&1&0&0&T \\ 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \end{array}} \right] \text{，} $$ $$ {\boldsymbol{\varGamma}} = \left[ {\begin{array}{*{20}{c}} {{T^2}/2}&0&0 \\ 0&{{T^2}/2}&0 \\ 0&0&{{T^2}/2} \\ T&0&0 \\ 0&T&0 \\ 0&0&T \end{array}} \right] 。 $$ 其中，
$ T $ 为采样周期。无人机配备的惯性导航器件加速度计测得的加速度
$ {{\boldsymbol{a}}_{m,}}_{k - 1} $ 和真实无人机飞行加速度$ {{\boldsymbol{a}}_{k - 1}} $ 之间存在随机误差，即$$ {{\boldsymbol{a}}_{k - 1}} = {{\boldsymbol{a}}_{m,}}_{k - 1} + {{\boldsymbol{w}}_{k - 1}} $$ (2) 式中，
$ {{\boldsymbol{w}}_{k - 1}} $ 为高斯白噪声，即$ {{\boldsymbol{w}}_k}\sim(0,{\boldsymbol{Q}}) $ 。同时无人机还可接收到外部高精度的民用卫星信号，可得无人机的观测方程为：
$$ {{\boldsymbol{Z}}_k} = {\boldsymbol{H}}{{\boldsymbol{X}}_k} + {{\boldsymbol{V}}_k} $$ (3) 式中：
$ {{\boldsymbol{Z}}_k} $ 为卫星信号提供的位置和速度信息；$ {{\boldsymbol{V}}_k} $ 为观测噪声，为高斯白噪声，$ {{\boldsymbol{V}}_k}\sim(0,{\boldsymbol{R}}) $ ；$ {\boldsymbol{H}} $ 为观测矩阵，且$$ {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&0&0&0 \\ 0&0&1&0&0&0 \\ 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \end{array}} \right] 。 $$ 利用离散型卡尔曼滤波方法求取式（1）的状态估计值
$ {\hat {\boldsymbol{X}}_k} $ ，即$$ {{\hat {\boldsymbol{X}}}_k} = {\boldsymbol{\varPhi}} {{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {{\boldsymbol{a}}_{m,k - 1}} + {{\boldsymbol{L}}_k}\left[ {{{\boldsymbol{Z}}_k} - {\boldsymbol{H}}\left( {{\boldsymbol{\varPhi}} {{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma }}{{\boldsymbol{a}}_{m,k - 1}}} \right)} \right] $$ (4) 式中，
$ {\boldsymbol{L}}_k $ 为卡尔曼滤波器稳态增益，且$$ \quad \quad \quad \quad {{\boldsymbol{L}}_k} = {{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{H}}^{\rm{T}}}{\left[ {{\boldsymbol{H}}{{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{H}}^{\rm{T}}} + {\boldsymbol{R}}} \right]^{ - 1}} $$ (5) 式中，
$ {{\boldsymbol{P}}_{k\left| {k - 1} \right.}} $ 为一步预测协方差矩阵，可由离散时间代数黎卡提方程求解，即$$ \begin{aligned}[b] {{\boldsymbol{P}}_{k\left| {k - 1} \right.}} =& {\boldsymbol{\varPhi}} {{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{\varPhi}} ^{\rm{T}}} - \\& {\boldsymbol{ \varPhi}} {{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{H}}^{\rm{T}}}{\left[ {{\boldsymbol{H}}{{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{H}}^{\rm{T}}} + {\boldsymbol{R}}} \right]^{ - 1}}{\boldsymbol{H}}{{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{{\boldsymbol{\varPhi}} ^{\rm{T}}} + {\boldsymbol{\varGamma}} {\boldsymbol{Q}}{{\boldsymbol{\varGamma }}^{\rm{T}}} \end{aligned} $$ (6) 无人机的控制目标是跟踪参考轨迹
${\overline {\boldsymbol{X}}_k} = [ {{{\bar r}_{x,k}}}\quad{{{\bar r}_{y,k}}} {{{\bar r}_{{\textit{z}},k}}}\quad{{{\bar v}_{x,k}}}\quad {{{\bar v}_{y,k}}}\quad{{{\bar v}_{{\textit{z}},k}}} ]^{\rm{T}}$ ，本文采用PID算法对无人机实施轨迹跟踪控制，则无人机控制输入量${{\boldsymbol{a}}_k}$ 为:$$ {{\boldsymbol{a}}_k} = - {\boldsymbol{K}}\left( {{{\hat {\boldsymbol{X}}}_k} - {{\bar {\boldsymbol{X}}}_k}} \right) $$ (7) 式中，K为无人机控制参数矩阵。
2. 基于逐点偏移式卫星导航欺骗干扰方法
下面以单步1维无人机位置欺骗原理步骤分析入手，研究一种基于逐点偏移式卫星导航欺骗干扰方法。
2.1 单步无人机位置欺骗原理分析
结合无人机的组合导航和飞行控制模型，单点无人机位置欺骗实现过程可分为6个步骤，具体如下所示。
步骤1：由于攻击方需要根据无人机真实位置
$ {{\boldsymbol{X}}_k} $ 来实时调整产生的虚假卫星信号。因此准确掌握无人机当前时刻真实运动状态信息$ {{\boldsymbol{X}}_k} $ 是实施欺骗攻击的前提。本文利用外部传感器（如相控阵雷达、无源频谱探测设备等）实时估算无人机的状态
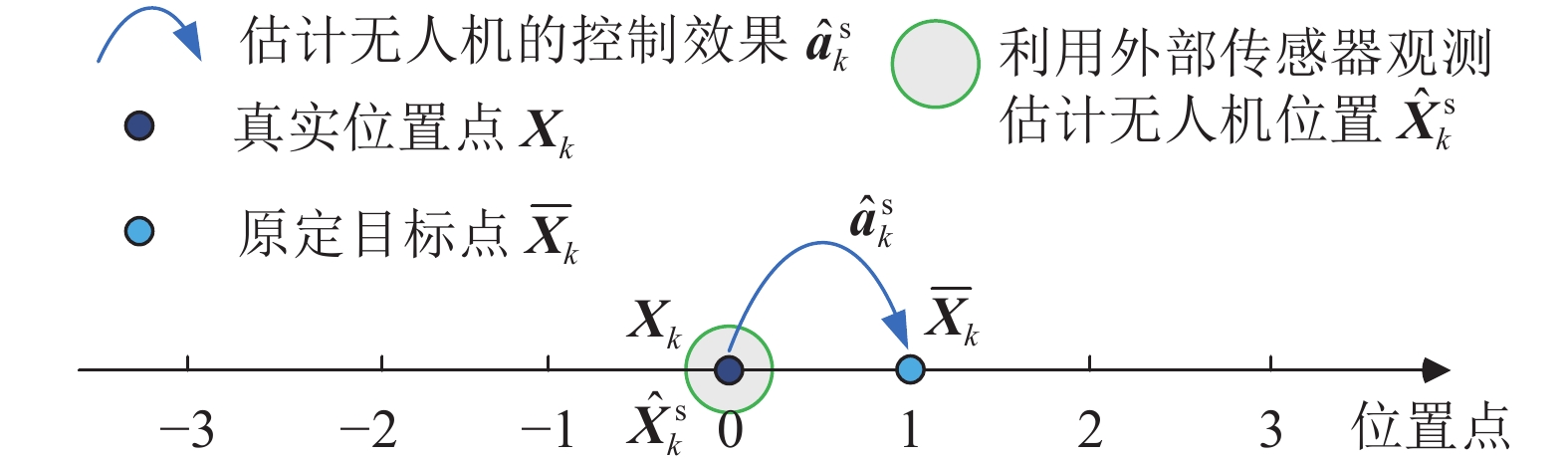
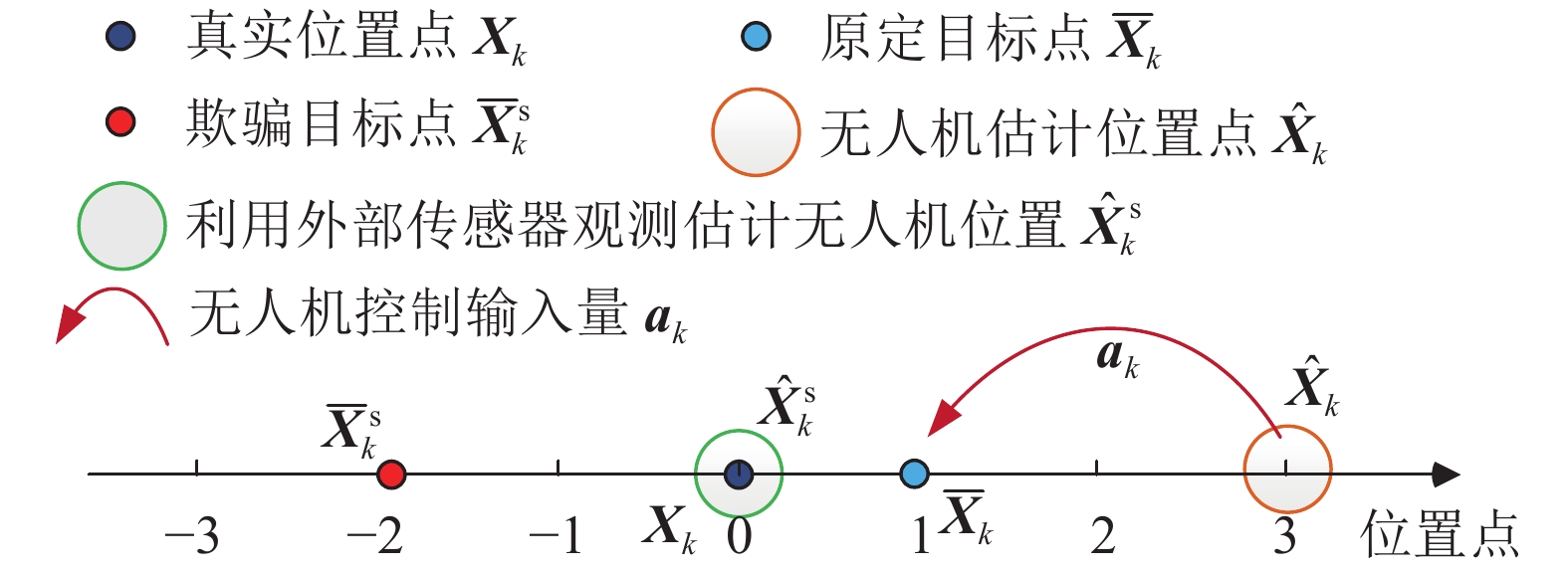
$ \hat {\boldsymbol{X}}_k^{\text{s}} $ 和加速度信息$ \hat {\boldsymbol{a}}_k^{\text{s}} $ ，如图2所示。从图2中可以看出，攻击方估计的无人机状态$ \hat {\boldsymbol{X}}_k^{\text{s}} $ 与真实状态$ {{\boldsymbol{X}}_k} $ 之间存在小范围的偏差，但不会影响$ \hat {\boldsymbol{a}}_k^{\text{s}} $ 的控制效果趋势，它会使得无人机跟踪参考轨迹上原定的目标点$ \overline {\boldsymbol{X}}_k^{} $ 。
图 2 k时刻无人机的飞行状态信息图Fig. 2 Diagram of UAV flight staus information at time k下载:
全尺寸图片
步骤2：设置欺骗目标点，计算欺骗控制输入量
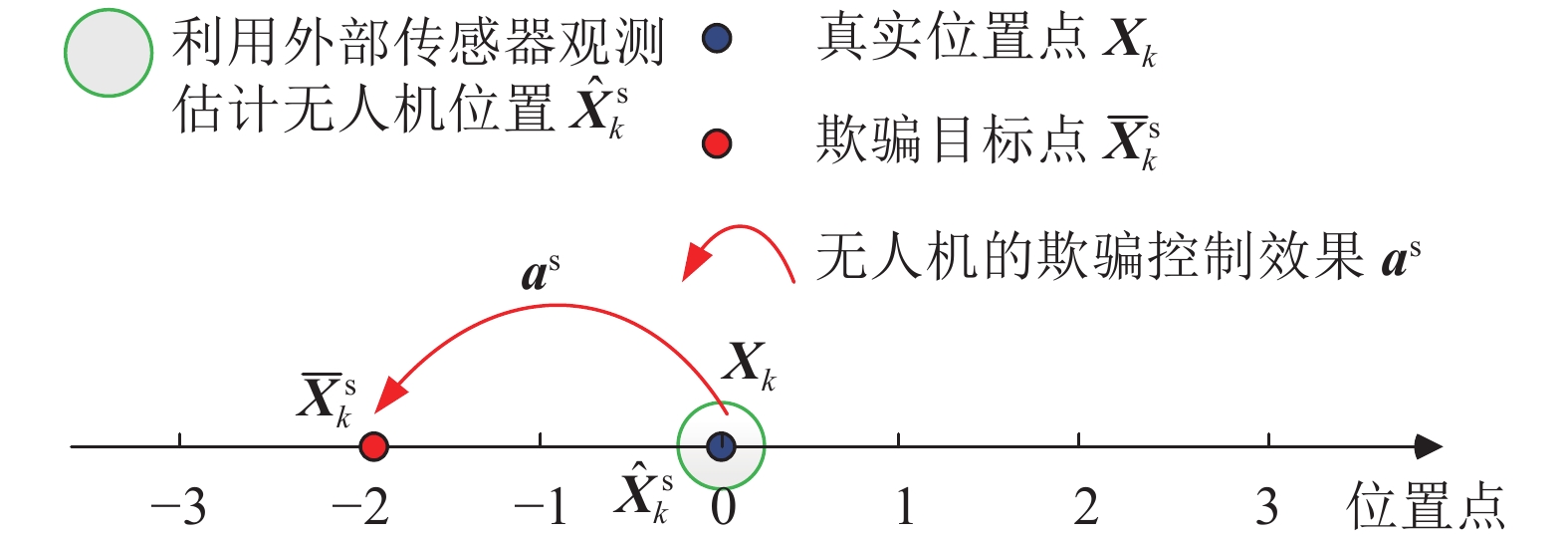
$ {{\boldsymbol{a}}^{\rm{s}}} $ ，即$$ {{\boldsymbol{a}}^{\rm{s}}} = - {{\boldsymbol{K}}^{\rm{s}}}\left( {\hat {\boldsymbol{X}}_k^{\text{s}} - \overline {\boldsymbol{X}}_k^{\text{s}}} \right) $$ (8) 式中，
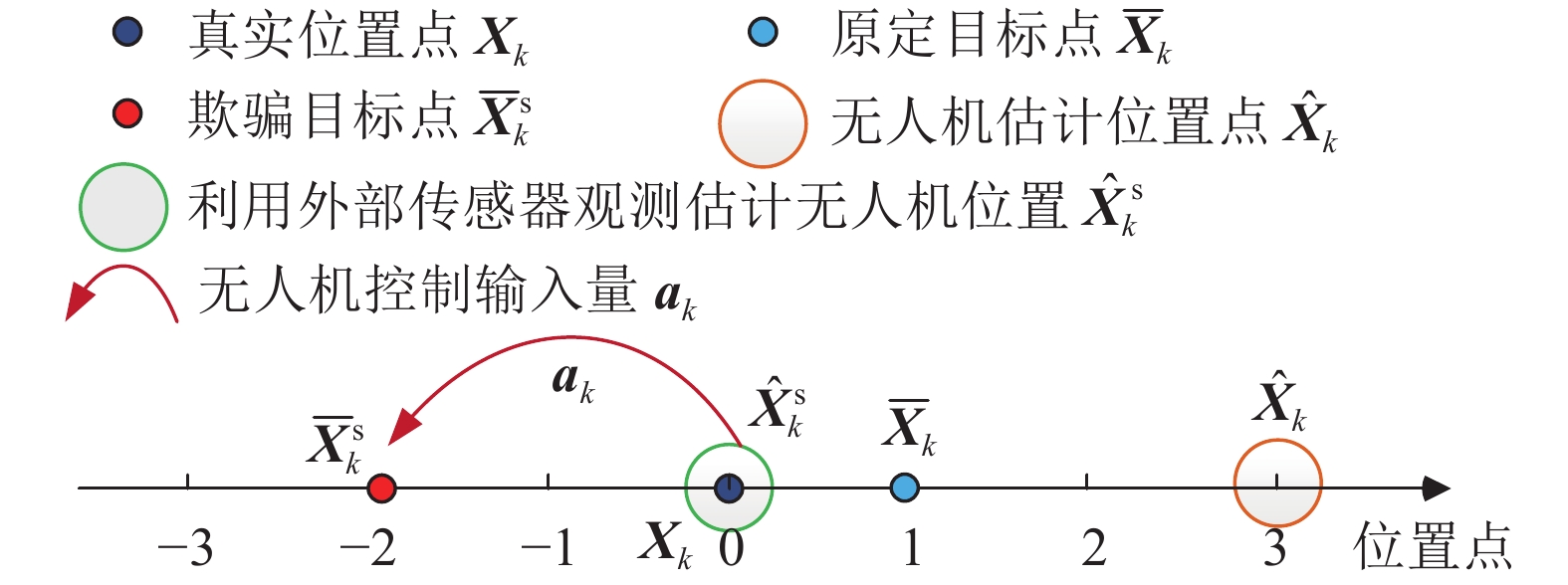
$ {{\boldsymbol{K}}^{\rm s}} $ 为欺骗控制参数矩阵，$\overline {\boldsymbol{X}}_k^{\text{s}}$ 为欺骗攻击方设定的欺骗参考轨迹。$ {{\boldsymbol{a}}^{\rm{s}}} $ 产生的控制效果如图3所示。从图3中可以看出，$ {{\boldsymbol{a}}^{\rm{s}}} $ 的控制效果是将无人机往欺骗参考轨迹$ \overline {\boldsymbol{X}}_k^{\text{s}} $ 缓慢靠近飞行。
图 3 k时刻无人机的欺骗控制效果图Fig. 3 Diagram of UAV soppfing control effect at time k下载:
全尺寸图片
步骤3：设计如式（9）所述的虚假卫星信号为：
$$ {\boldsymbol{X}}_k^* = {\boldsymbol{\varPhi}} {\boldsymbol{X}}_{k - 1}^* + {\boldsymbol{\varGamma}} {\boldsymbol{a}}_{k - 1}^* $$ (9) 式中，
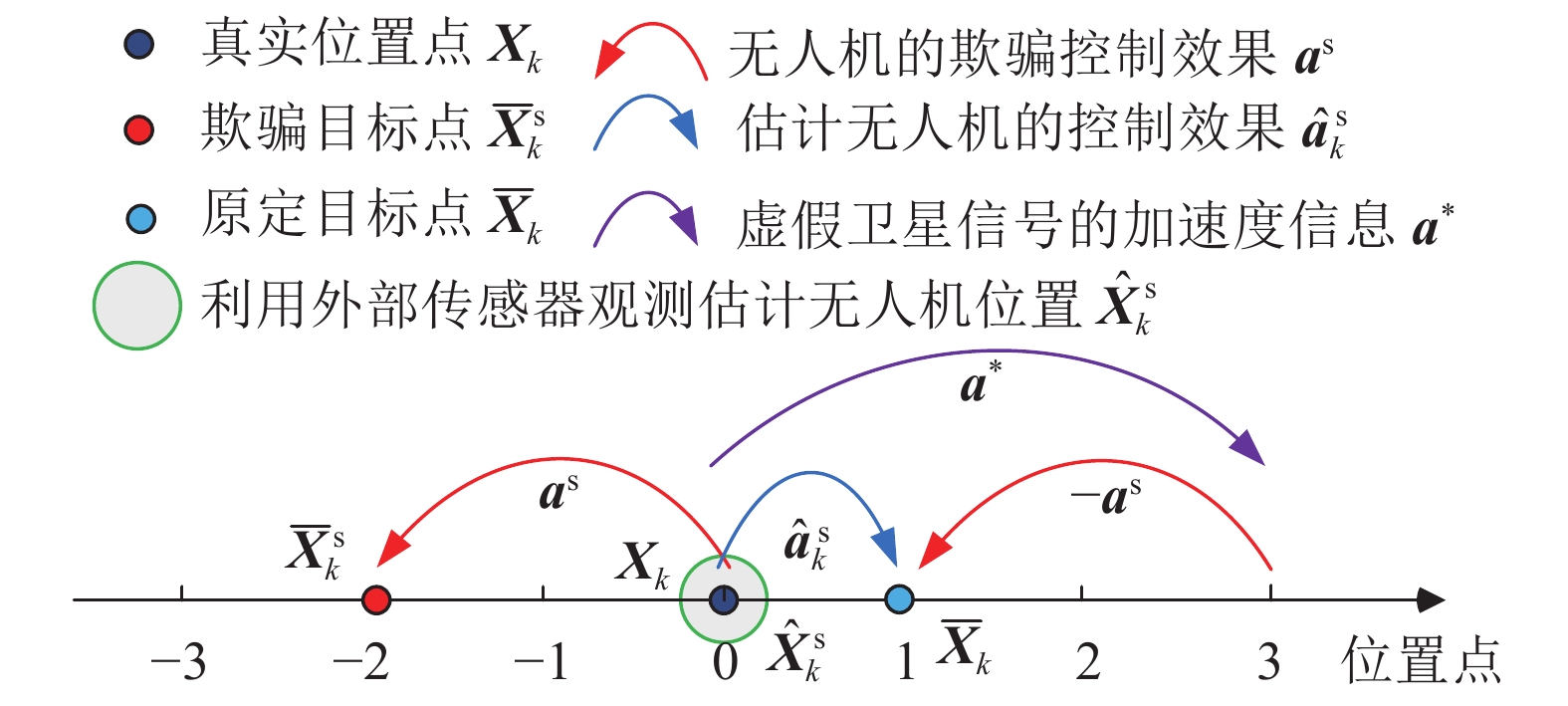
$ {\boldsymbol{X}}_k^* $ 为外部构造的虚假卫星信号，在进行卡尔曼滤波数据融合时可等效于式（3）中的观测矢量$ {\boldsymbol{Z}}_{k} $ 。$ {\boldsymbol{a}}_k^* $ 为虚假卫星信号中的加速度信息：$$ {\boldsymbol{a}}_k^* = \hat {\boldsymbol{a}}_k^{\text{s}} - {{\boldsymbol{a}}^{\rm{s}}} $$ (10) 图4描述了
$ {\boldsymbol{a}}_k^* $ 、$ {{\boldsymbol{a}}^{\rm{s}}} $ 和$ \hat {\boldsymbol{a}}_k^{\text{s}} $ 之间的空间对应关系。从图4中可以看出，本文提出的单步无人机位置欺骗原理设想是充分考虑无人机飞行控制器对卫星导航欺骗的影响，即虚假卫星信号中的加速度信息$ {\boldsymbol{a}}_k^* $ 是在欺骗控制输入量$ {{\boldsymbol{a}}^{\rm{s}}} $ 的基础上抵消无人机本身飞行控制器$ \hat {\boldsymbol{a}}_k^{\text{s}} $ 影响下产生获得的。
图 4 生成虚假卫星信号的加速度信息效果图Fig. 4 Diagram of acceleration information effect for generating false satellite signals下载:
全尺寸图片
步骤4：根据式（4），可得施加虚假GNSS信号改变无人机组合导航滤波估计状态
$ {\hat {\boldsymbol{X}}_k} $ 为：$$ {{\hat {\boldsymbol{X}}}_k} = {\boldsymbol{\varPhi}} {{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {{\boldsymbol{a}}_{m,k - 1}} + {{\boldsymbol{L}}_k}\left[ {{\boldsymbol{X}}_k^* - {\boldsymbol{H}}\left( {{\boldsymbol{\varPhi}} {{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {{\boldsymbol{a}}_{m,k - 1}}} \right)} \right] $$ (11) 式中，
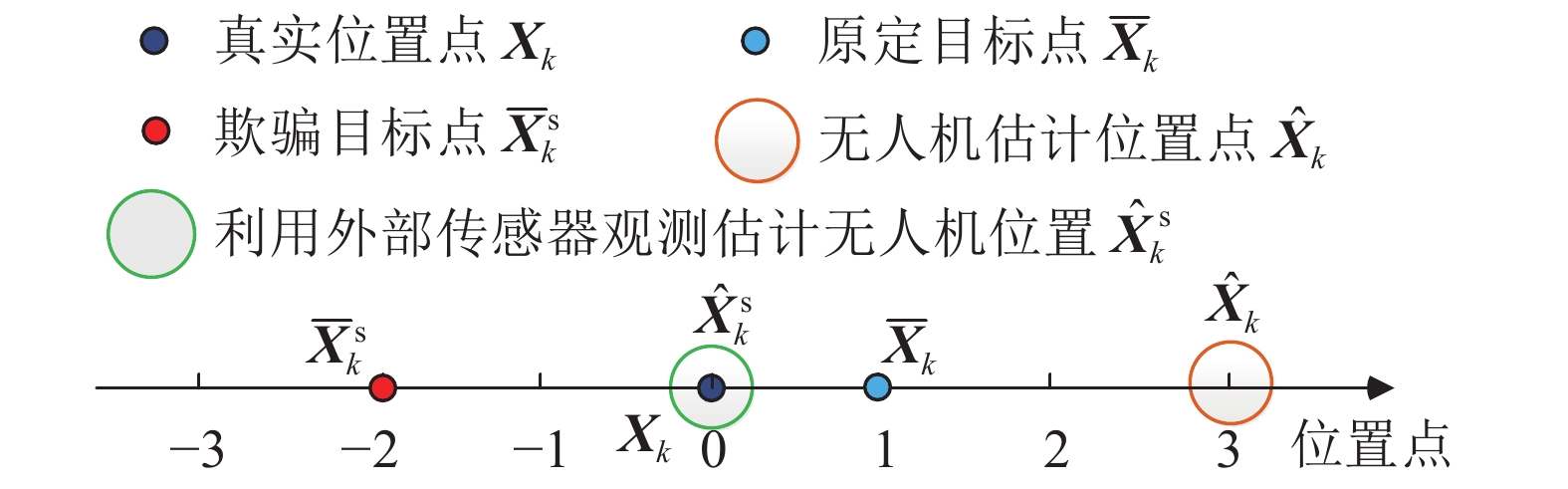
$ {\boldsymbol{X}}_k^* $ 为虚假卫星信号，可通过虚假卫星信号中的加速度信息$ {\boldsymbol{a}}_k^* $ 积分计算获得。图5描述了施加虚假GNSS信号后无人机滤波估计状态图。从图5可以看出，虚假卫星信号的接入使得无人机组合导航滤波估计位置值
$ {\hat {\boldsymbol{X}}_k} $ 已经偏离了真实位置点$ {{\boldsymbol{X}}_k} $ 。
图 5 无人机被欺骗后滤波估计定位效果图Fig. 5 Diagram of filtering UAV estimated position after being spoofed下载:
全尺寸图片
步骤5：此时无人机会产生靠近目标点
$ {\overline {\boldsymbol{X}}_k} $ 的控制效果，如图6所示。由图6分析可知，控制效果$ {{\boldsymbol{a}}_k} $ 根据欺骗后错误的组合导航滤波估计结果并结合式（7）获得的。
图 6 无人机被欺骗后产生靠近目标点控制效果图Fig. 6 Diagram of generating control near the target point after UAV being spoofed下载:
全尺寸图片
步骤6：无人机实施控制的效果如图7所示。从图7可以看出，将控制效果
$ {{\boldsymbol{a}}_k} $ 施加到无人机真实位置点$ {{\boldsymbol{X}}_k} $ 上，就会驱使无人机缓慢靠近欺骗目标点，最终达到欺骗攻击的目的。
图 7 将控制效果施加无人机真实位置点上效果图Fig. 7 Diagram of applying the control effect to the real UAV position point下载:
全尺寸图片
从整个单步无人机位置欺骗实现过程中可以得到如下结论：
1）无人机位置欺骗是通过施加虚假GNSS信号实现的。从步骤3、4中可知，其具体实现过程是，虚假GNSS信号与无人机惯性系统测得的信号进行组合导航滤波数据融合，产生错误的无人机估计信息，这个错误的无人机估计信息会根据式（7）产生新的控制量，叠加到无人机控制系统中，导致无人机不再跟踪原定目标点，而靠近欺骗目标点，实现位置的欺骗偏移。
2）欺骗的实现需要有一个不同于GNSS信号的外部传感器对无人机的状态进行观测。从步骤1可知，为了在设计计算虚假GNSS信号中，抵消原始无人机控制器的影响，需要预先知道原始无人机轨迹跟踪控制输入量，即此刻无人机的加速度，这个量可通过除卫星之外的外部传感器测得，如相控阵雷达、无源频谱探测设备等。
3）精确的欺骗定位需要对虚假GNSS信号进行构造设计。从步骤3可知，虚假GNSS信号是通过虚假GNSS信号的加速度信息（即控制输入量）积分求得的，同时，求取虚假GNSS控制输入量需要在无人机真实控制输入量中抵消掉欺骗轨迹跟踪控制器的影响。
2.2 基于逐点偏移的无人机欺骗方案设计
将上述单步无人机位置欺骗方法进行时间和维数的扩展，设计一种长时间的、多维的无人机位置欺骗方案，即基于逐点偏移式卫星导航欺骗干扰方案。逐点偏移的意思是对于每个时刻的无人机位置点，在水平和垂直方向上都利用单步无人机位置欺骗方法，实现各个位置方向上的逐点欺骗偏移。
无人机位置欺骗方案的实现需要实时跟踪无人机的真实状态，该状态可根据无人机自身的运动学模型，以及外部的无人机量测信息（外部传感器精度较高，忽略测量误差，可近似等于无人机的真实状态X ），采用线性滤波估计器近似得到无人机的真实飞行状态
$ \hat {\boldsymbol{X}}_k^{\text{s}} $ 和加速度信息$ \hat {\boldsymbol{a}}_k^{\text{s}} $ ：$$ \quad \quad \quad \hat {\boldsymbol{X}}_k^{\text{s}} ={\boldsymbol{ \varPhi}} \hat{\boldsymbol{ X}}_{k - 1}^{\text{s}} + {\boldsymbol{\varGamma }}\hat {\boldsymbol{a}}_{k - 1}^{\text{s}} + {\boldsymbol{L}}_x^{\text{s}}\left[ {{\boldsymbol{X}}_{k - 1}^{} - \hat {\boldsymbol{X}}_{k - 1}^{\rm{s}}} \right] $$ (12) $$ \hat {\boldsymbol{a}}_k^{\text{s}} = {\boldsymbol{L}}_a^{\text{s}}\left[ {{\boldsymbol{X}}_{k - 1}^{} - \hat {\boldsymbol{X}}_{k - 1}^{\text{s}}} \right] $$ (13) 并且，
${{\boldsymbol{L}}^{\text{s}}} = {[{({\boldsymbol{L}}_x^{\text{s}})^{\rm{T}}},{({\boldsymbol{L}}_a^{\text{s}})^{\rm{T}}}]^{\rm{T}}}$ 为欺骗攻击方的卡尔曼滤波器稳态增益，可由离散时间代数黎卡提方程求解。虚假GNSS信号加速度
$ {{\boldsymbol{a}}^*} $ 的估算需要在真实控制输入量中抵消掉跟踪欺骗轨迹的控制影响，即${\boldsymbol{a}}_k^* = \hat {\boldsymbol{a}}_k^{\text{s}} - {{\boldsymbol{a}}^{\text{s}}}$ ，其中，$ {{\boldsymbol{a}}^{\text{s}}} $ 为无人机跟踪欺骗目标点的控制输入量，且${{\boldsymbol{a}}^{\text{s}}} = - {{\boldsymbol{K}}^{\text{s}}}\left( {\hat {\boldsymbol{X}}_k^{\text{s}} - \overline {\boldsymbol{X}}_k^{\text{s}}} \right)$ 。进一步利用无人机的运动学模型积分计算得到虚假卫星信号，即${\boldsymbol{X}}_k^* ={\boldsymbol{ \varPhi}} {\boldsymbol{X}}_{k - 1}^* + {\boldsymbol{\varGamma}} {\boldsymbol{a}}_{k - 1}^*$ ，然后将此虚假GNSS信号施加到无人机系统中，根据式（4）与惯性导航数据测得的状态信息进行滤波数据融合，得到错误的滤波估计量，进而根据式（7）重新计算系统输入控制量作用在无人机系统中，使得其真实位置点不再跟踪原始目标点，而向欺骗目标点发生偏移，实现位置的欺骗。综合上述，可得基于逐点偏移的无人机欺骗方案原理结构框图，如图8所示。由图8分析可知，欺骗方案的实施需要包括外部状态观测器、轨迹发生器、模拟无人机控制器及信号模拟器等设备模块，欺骗攻击方可根据利用轨迹发生器规划的欺骗轨迹和外部观测的参考轨迹，以及截取并接收到的真实卫星信号，在每一个攻击时刻依据第2.1节的单步无人机位置欺骗原理，实时构造能使得无人机发生精确位置偏移的虚假卫星信号。
图 8 无人机位置欺骗的结构设计框图Fig. 8 Diagram of applying the control effect to the real UAV position point下载:
全尺寸图片
3. 欺骗方案性能分析
根据无人机轨迹跟踪控制器和虚假GNSS信号的设计原理，分析基于逐点偏移式卫星导航欺骗干扰方案的有效性，即判断加入虚假的GNSS信号后，无人机真实位置点是否近似等于欺骗目标点。根据式（1）、（7）、（8）、（10）、（12）及（13），可得真实飞行状态
$ {{\boldsymbol{X}}_k} $ 与欺骗轨迹$ \overline {\boldsymbol{X}}_k^{\text{s}} $ 的差值为：$$ \begin{aligned}[b] {{\boldsymbol{X}}_k} - \overline {\boldsymbol{X}}_k^{\text{s}} =& {\boldsymbol{\varPhi}} {{\boldsymbol{X}}_{k - 1}} - {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\overline {\boldsymbol{X}}}_{k - 1}} - \overline {\boldsymbol{X}}_k^{\text{s}} = \\& {\boldsymbol{\varPhi}} {{\boldsymbol{X}}_{k - 1}} - {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\overline {\boldsymbol{X}}}_{k - 1}} - \hat {\boldsymbol{X}}_k^{\text{s}} + \\& {\left[ {{{\left( {{{\boldsymbol{K}}^{\text{s}}}} \right)}^{\rm{T}}}{{\boldsymbol{K}}^{\text{s}}}} \right]^{ - 1}}{\left( {{{\boldsymbol{K}}^{\text{s}}}} \right)^{\text{T}}}\left( {{\boldsymbol{a}}_k^* - \hat {\boldsymbol{a}}_k^{\text{s}}} \right) = \\& {\boldsymbol{\varPhi}} {{\boldsymbol{X}}_{k - 1}} - {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\overline {\boldsymbol{X}}}_{k - 1}} - \hat {\boldsymbol{X}}_k^{\text{s}} + \\& {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{a}}_k^* - {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}{{\boldsymbol{X}}_{k - 1}} + {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}\hat {\boldsymbol{X}}_{k - 1}^{\text{s}} = \\& {\boldsymbol{\varPhi}} {{\boldsymbol{X}}_{k - 1}} - {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\hat {\boldsymbol{X}}}_{k - 1}} + {\boldsymbol{\varGamma}} {\boldsymbol{K}}{{\overline {\boldsymbol{X}}}_{k - 1}} - {\boldsymbol{L}}_x^{\text{s}}{{\boldsymbol{X}}_{k - 1}} - \\& \left( {{\boldsymbol{\varPhi}} - {\boldsymbol{L}}_x^{\text{s}}} \right)\hat {\boldsymbol{X}}_{k - 1}^{\text{s}} - {\boldsymbol{\varGamma}} \hat {\boldsymbol{a}}_{k - 1}^{\text{s}} + {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{a}}_k^*{\kern 1pt} - \\& {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}{{\boldsymbol{X}}_{k - 1}} + {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}\hat {\boldsymbol{X}}_{k - 1}^{\text{s}} = \\& \left( {{\boldsymbol{\varPhi}} - {\boldsymbol{L}}_x^{\text{s}} - {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}} \right)\left( {{{\boldsymbol{X}}_{k - 1}} - \hat {\boldsymbol{X}}_{k - 1}^{\text{s}}} \right) - \\& {\boldsymbol{\varGamma}} {\boldsymbol{K}}\left( {{{\hat {\boldsymbol{X}}}_k} - {{\overline {\boldsymbol{X}}}_k}} \right) - {\boldsymbol{\varGamma}} \hat {\boldsymbol{a}}_k^{\text{s}} + {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{a}}_k^* = \\& \left( {{\boldsymbol{\varPhi}} -{\boldsymbol{ L}}_x^{\text{s}} - {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{L}}_a^{\text{s}}} \right)\left( {{{\boldsymbol{X}}_{k - 1}} - \hat {\boldsymbol{X}}_{k - 1}^{\text{s}}} \right) + \\& {\boldsymbol{\varGamma}} \left( {{{\boldsymbol{a}}_k} - \hat {\boldsymbol{a}}_k^{\text{s}}} \right) + {\boldsymbol{\varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right){\boldsymbol{a}}_k^*\\[-10pt] \end{aligned} $$ (14) 式中，
${\boldsymbol{ \varUpsilon}} \left( {{{\boldsymbol{K}}^{\text{s}}}} \right) = {\left[ {{{\left( {{{\boldsymbol{K}}^{\text{s}}}} \right)}^{\rm{T}}}{{\boldsymbol{K}}^{\text{s}}}} \right]^{ - 1}}{\left( {{{\boldsymbol{K}}^{\text{s}}}} \right)^{\text{T}}}$ 。由于
$ \hat {\boldsymbol{X}}_{k - 1}^{\text{s}} $ 、$ \hat {\boldsymbol{a}}_k^{\text{s}} $ 是利用外部传感器对无人机真实状态的估计量，则$ {{\boldsymbol{X}}_{k - 1}} \approx \hat {\boldsymbol{X}}_{k - 1}^{\text{s}} $ ，$ {{\boldsymbol{a}}_k} \approx \hat {\boldsymbol{a}}_k^{\text{s}} $ 。同时在构造虚假GNSS信号时，因为是逐点偏移设计的，因此$ {\boldsymbol{a}}_k^* $ 是小量。综上，可将式（14）进一步化简为：$$ {{\boldsymbol{X}}_k} - \overline {\boldsymbol{X}}_k^{\text{s}} \approx 0 $$ (15) 由此可知，在无人机真实状态的初始值和欺骗规划轨迹的起始点相同时，无人机的真实状态会始终跟踪欺骗轨迹的目标点，达到位置欺骗偏移的目的，从而验证了基于逐点偏移式卫星导航欺骗干扰方案的有效性。
4. 仿真分析
为验证基于逐点拉偏式卫星导航欺骗算法的有效性和正确性，本文拟进行两组实验。
实验1：无人机规划的参考轨迹和欺骗攻击方设定的欺骗轨迹均为3维曲线型，即：
$$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{}=0.01\mathrm{sin}(0.01t)，\\ {\bar{{\boldsymbol{a}}}}_{y}^{}=0.01\mathrm{cos}(0.01t)，\\ {\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0.000\;1；\end{array} \right.$$ $$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{x}^{}+0.000\text{ }1，\\ {\bar{{\boldsymbol{a}}}}_{y}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{y}^{}-0.000\text{ }1，\\ {\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}+0.000\text{ }06。\end{array}\right. $$ 其中，所有加速度的单位为
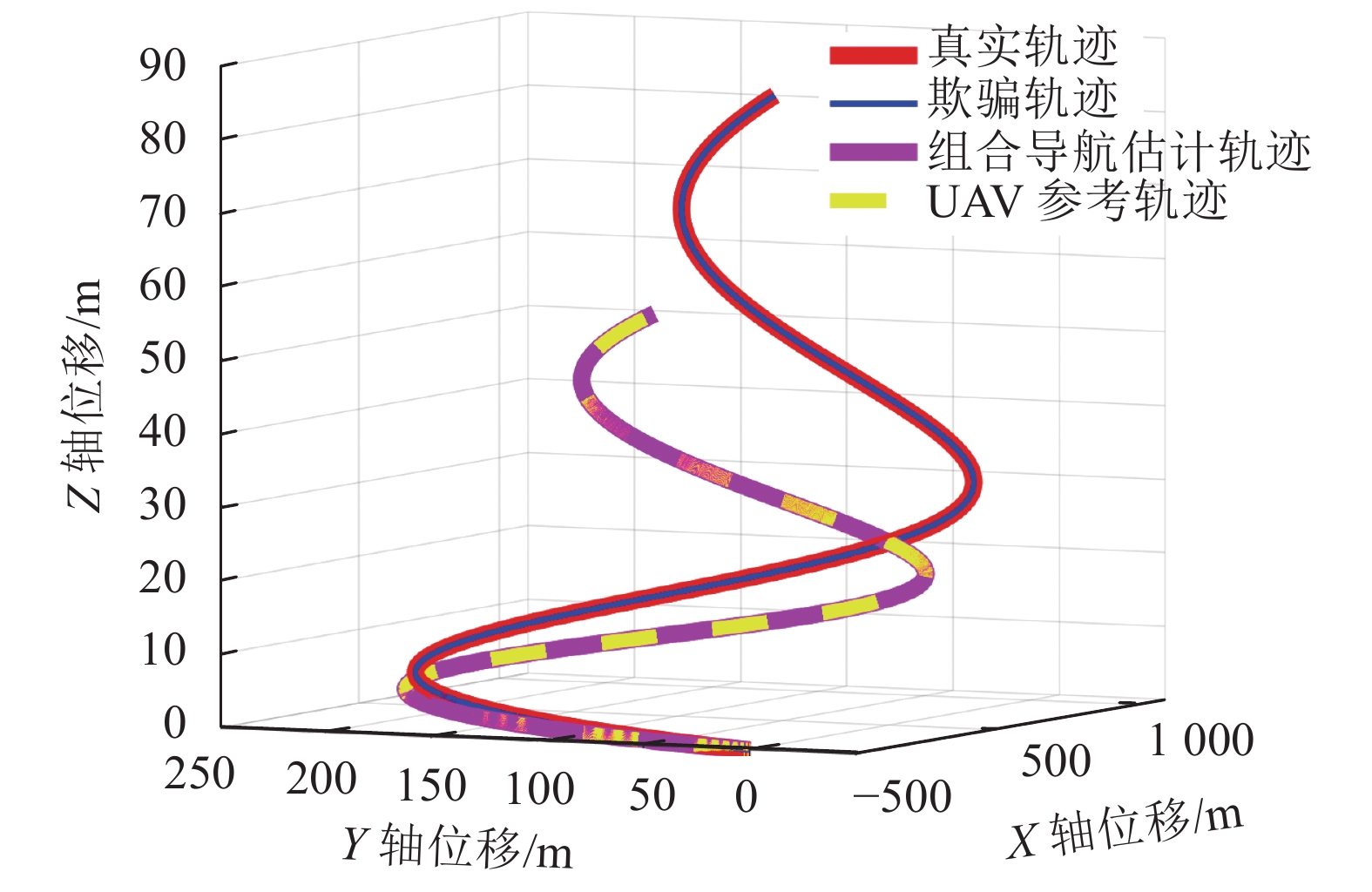
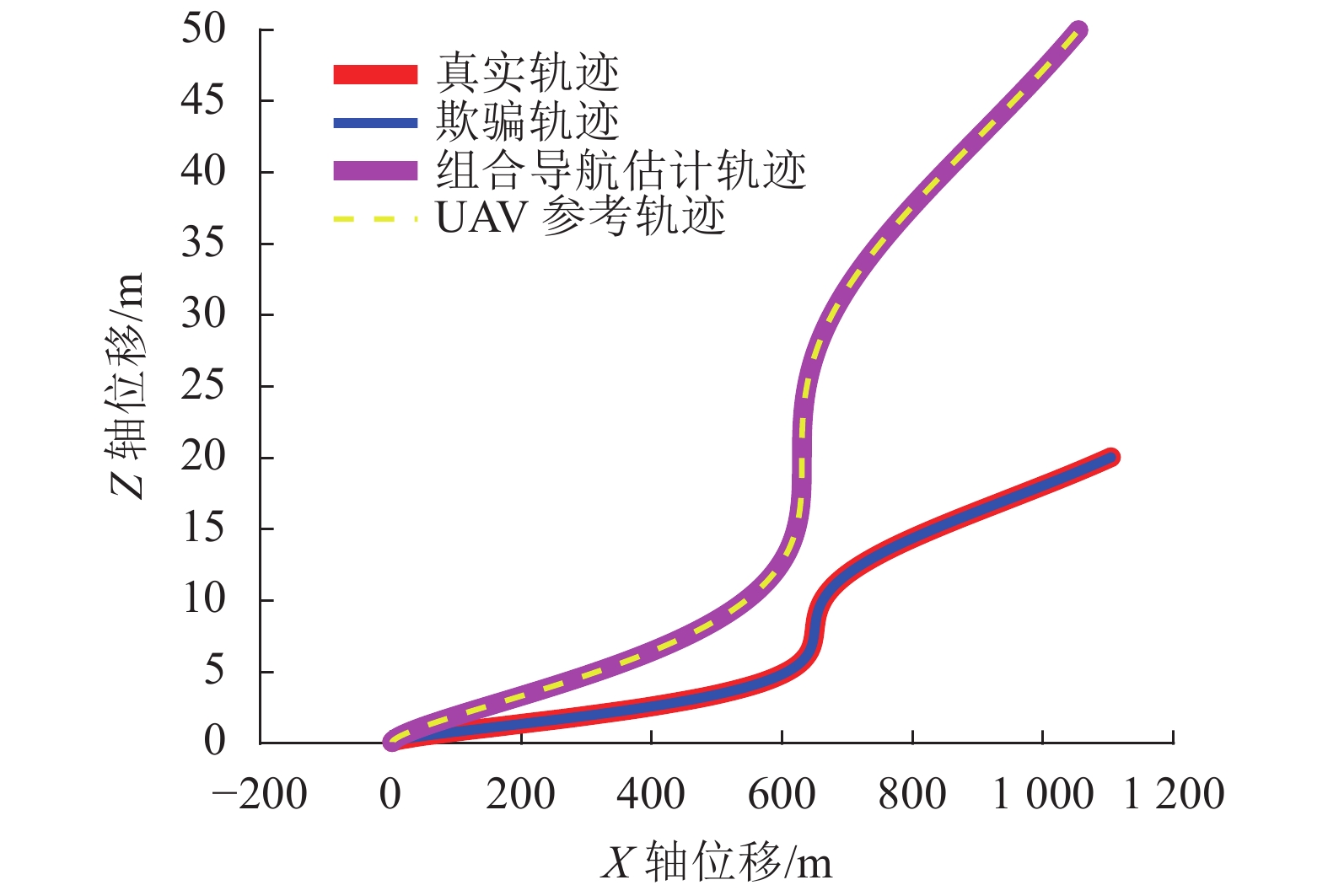
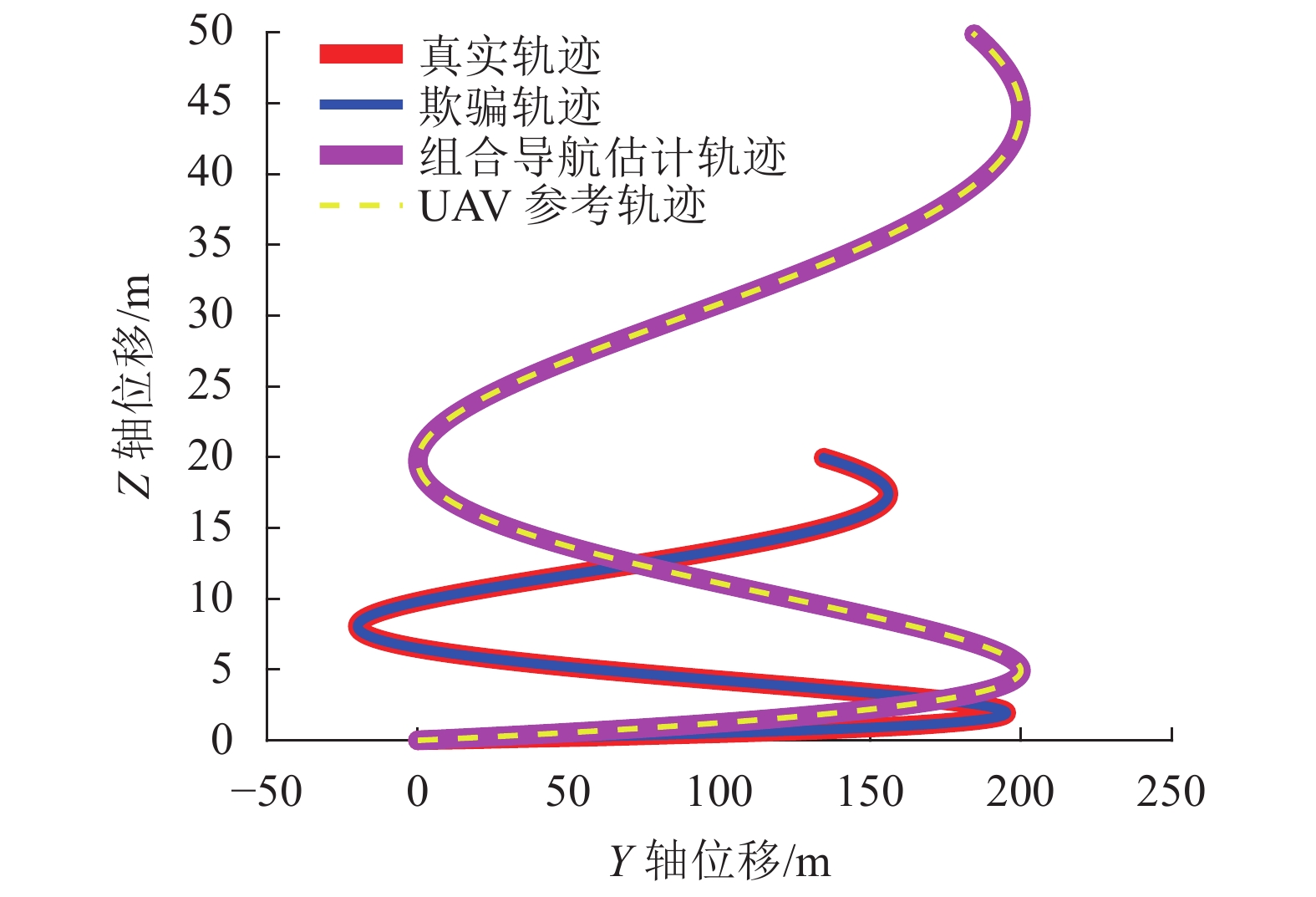
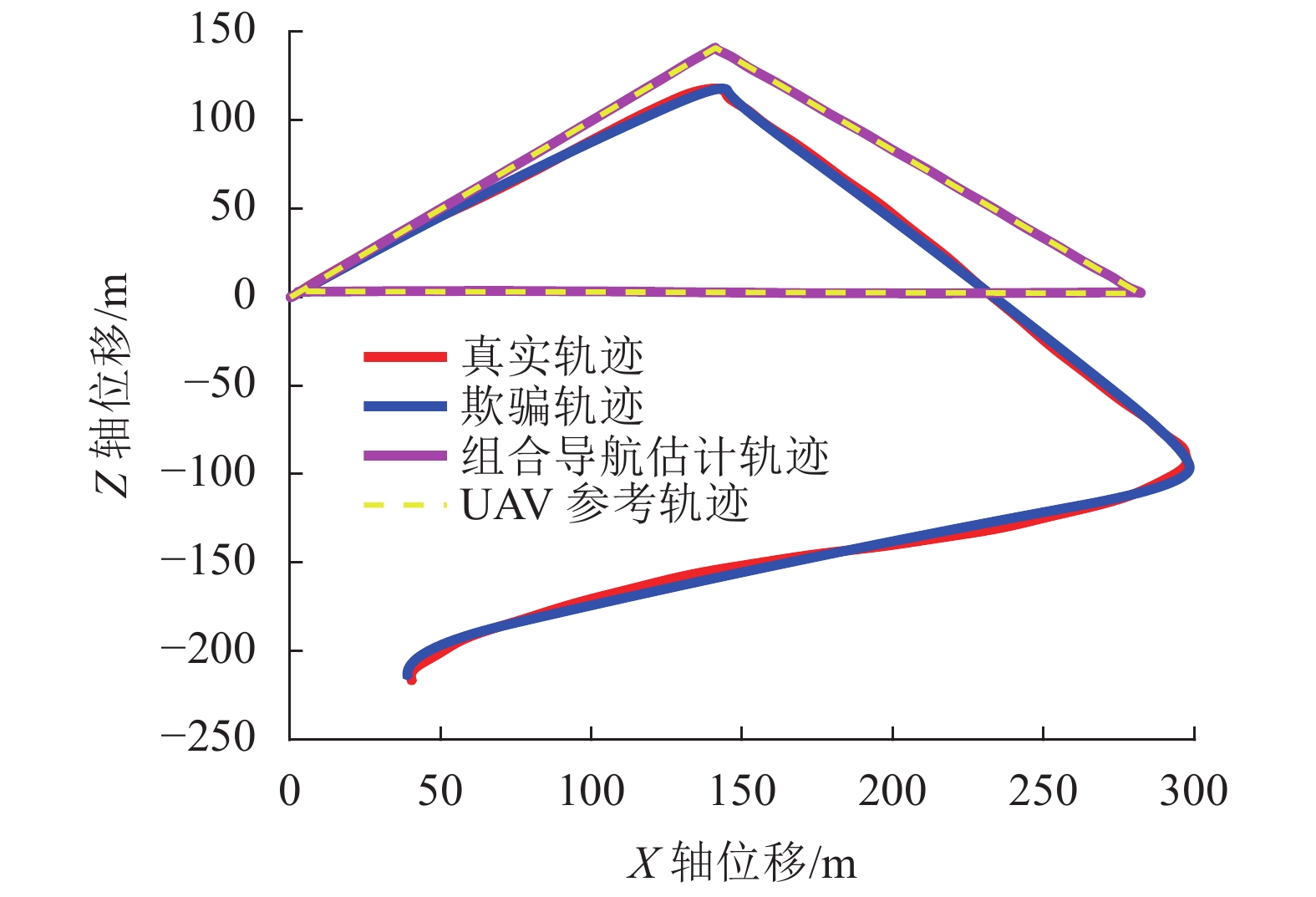
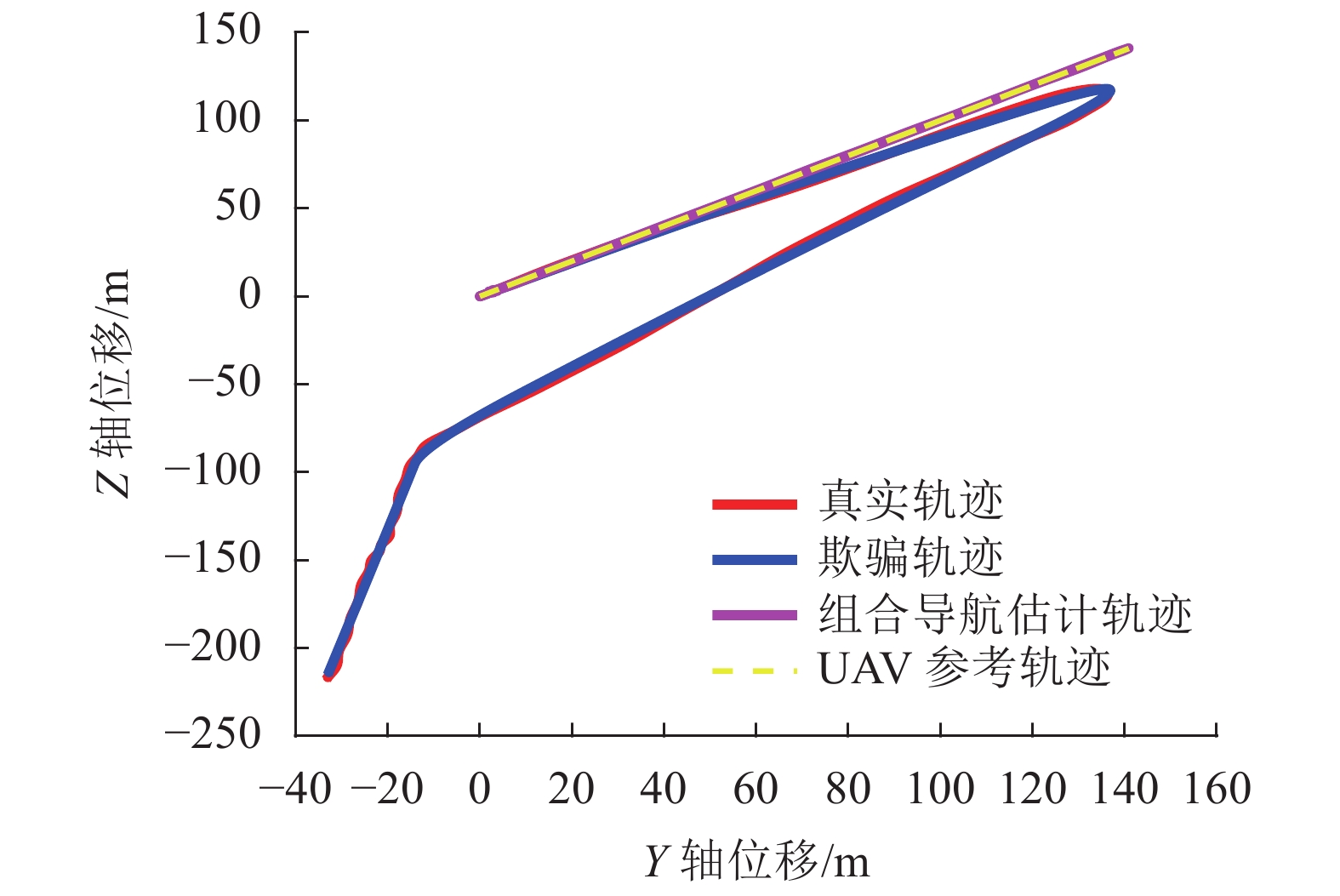
$ {\text{m/}}{{\text{s}}^{\text{2}}} $ 。实验的仿真时间为1 000 s。设置无人机和欺骗控制器参数矩阵分别为：$$ {\boldsymbol{K}} = {\left[ {\begin{array}{*{20}{c}} 1&2&{0.1}&1&{0.01}&{0.1} \\ 1&2&1&2&{0.1}&{0.02} \\ 1&2&1&2&1&2 \end{array}} \right]^{\rm{T}}} \text{，} $$ $$ {{\boldsymbol{K}}^{\rm s}} = {\left[ {\begin{array}{*{20}{c}} {0.01}&{0.1}&0&0&0&0 \\ 0&0&{0.01}&{0.1}&0&0 \\ 0&0&0&0&{0.01}&{0.01} \end{array}} \right]^{\rm{T}}} 。 $$ 图9给出了3维无人机跟踪曲线轨迹的欺骗效果，图10～12给出了任意两个方向的2维投影仿真效果图。其中，红线表示真实轨迹，蓝线表示参考的欺骗轨迹，紫线表示无人机组合导航估计轨迹，黄线表示原始期望参考轨迹。
图 9 3维无人机跟踪曲线轨迹的欺骗效果图Fig. 9 Diagram of spoofing effect of three-dimensional UAV tracking curve trajectory下载:
全尺寸图片
图 10 X和Y方向上的曲线轨迹跟踪欺骗效果图Fig. 10 Diagram of tracking curve trajectory spoofing effect in X and Y directions下载:
全尺寸图片
图 11 X和Z方向上的曲线轨迹跟踪欺骗效果图Fig. 11 Diagram of tracking curve trajectory spoofing effect in X and Z directions下载:
全尺寸图片
图 12 Y和Z方向上的曲线轨迹跟踪欺骗效果图Fig. 12 Diagram of tracking curve trajectory spoofing effect in Y and Z directions下载:
全尺寸图片
从图9～12中看出，施加利用基于逐点偏移式卫星导航欺骗干扰方法设计的虚假GNSS信号后，无人机真实位置点能够在任何方向上都跟踪欺骗轨迹运动，同时无人机组合导航滤波器估计轨迹仍输出原始参考轨迹，实现了无人机卫星导航欺骗的效果。
实验2：在相同无人机和欺骗控制器参数矩阵的情况下，无人机规划的参考轨迹和欺骗攻击方设定的欺骗轨迹均为3维折线型，即：
1）3维折线型参考轨迹的加速度分量为：
第1条边：
$$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{}=0.1,{\bar{{\boldsymbol{a}}}}_{y}^{}=0.1,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0.1,t\in [0,20)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=0,{\bar{{\boldsymbol{a}}}}_{y}^{}=0,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0,t\in [20,70)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=-0.1,{\bar{{\boldsymbol{a}}}}_{y}^{}=-0.1,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=-0.1,t\in [70,90)。\end{array} \right.$$ 第2条边：
$$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{}=0.1,{\bar{{\boldsymbol{a}}}}_{y}^{}=-0.1,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=-0.1,t\in [90,110)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=0,{\bar{{\boldsymbol{a}}}}_{y}^{}=0,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0,t\in [110,160)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=-0.1,{\bar{{\boldsymbol{a}}}}_{y}^{}=0.1,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0.1,t\in [160,180)。\end{array} \right.$$ 第3条边：
$$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{}=-0.2,{\bar{{\boldsymbol{a}}}}_{y}^{}=0,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0,t\in [180,200)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=0,{\bar{{\boldsymbol{a}}}}_{y}^{}=0,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0,t\in [200,250)；\\ {\bar{{\boldsymbol{a}}}}_{x}^{}=-0.2,{\bar{{\boldsymbol{a}}}}_{y}^{}=0,{\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}=0.1,t\in [250,270)。\end{array} \right.$$ 2）3维折线型欺骗轨迹的加速度分量为：
$$ \left\{ \begin{array}{l}{\bar{{\boldsymbol{a}}}}_{x}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{x}^{}+0.001，\\ {\bar{{\boldsymbol{a}}}}_{y}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{y}^{}-0.001，\\ {\bar{{\boldsymbol{a}}}}_{{{\textit{z}}}}^{\text{s}}={\bar{{\boldsymbol{a}}}}_{{\textit{z}}}^{}-0.006。\end{array} \right.$$ 其中，所有加速度的单位为
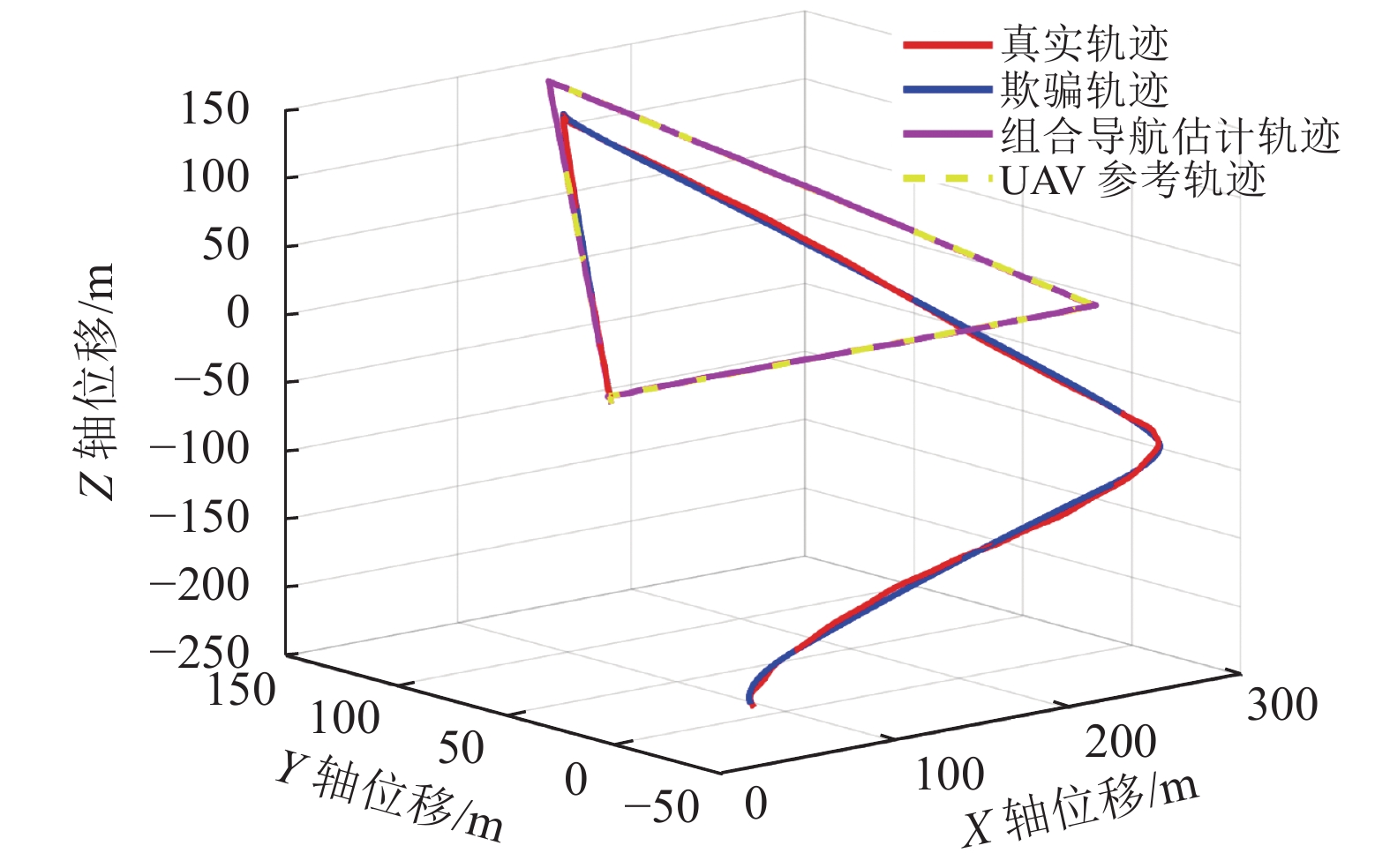
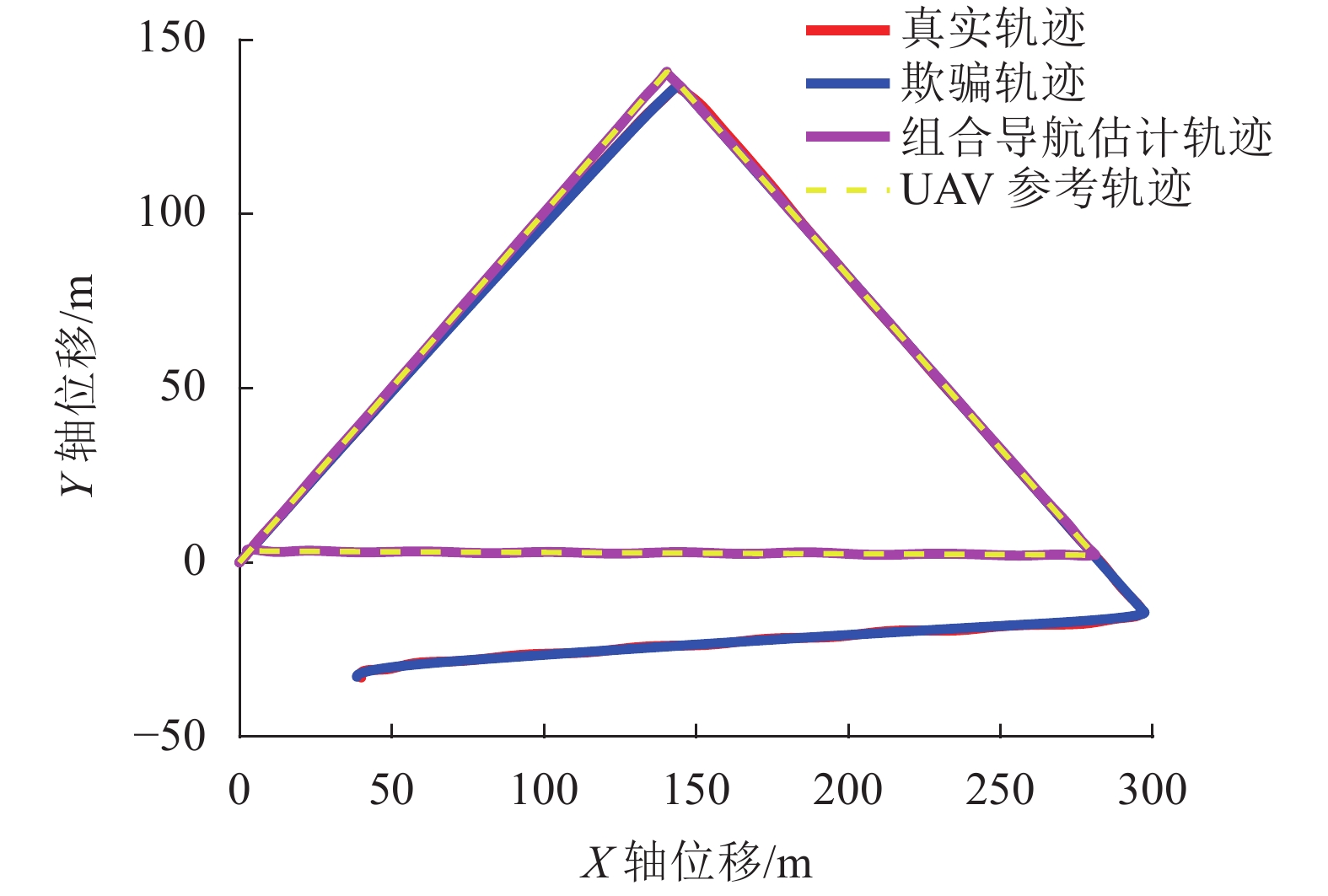
$ {\text{m/}}{{\text{s}}^{\text{2}}} $ 。实验的仿真时间为270 s。图13给出了3维无人机折线轨迹欺骗器效果图，图14～16给出了任意两个方向的2维投影仿真效果图。
图 13 3维无人机跟踪折线轨迹的欺骗效果图Fig. 13 Diagram of spoofing effect of three-dimensional UAV tracking line trajectory下载:
全尺寸图片
图 14 X和Y方向上的折线轨迹跟踪欺骗效果图Fig. 14 Diagram of tracking line trajectory spoofing effect in X and Y directions下载:
全尺寸图片
图 15 X和Z方向上的折线轨迹跟踪欺骗效果图Fig. 15 Diagram of tracking line trajectory spoofing effect in X and Z directions下载:
全尺寸图片
图 16 Y和Z方向上的折线轨迹跟踪欺骗效果图Fig. 16 Diagram of tracking line trajectory spoofing effect in Y and Z directions下载:
全尺寸图片
从图13～16中可以看出，利用逐基于逐点偏移式卫星导航欺骗干扰方法跟踪折线轨迹也能使得无人机慢慢偏离原始轨迹而跟踪欺骗轨迹，且无人机组合导航滤波器估计轨迹仍跟踪原始参考轨迹，达到了卫星导航欺骗的目的。综合两组实验结果分析论证了逐点拉偏式卫星导航欺骗算法的有效性和正确性。
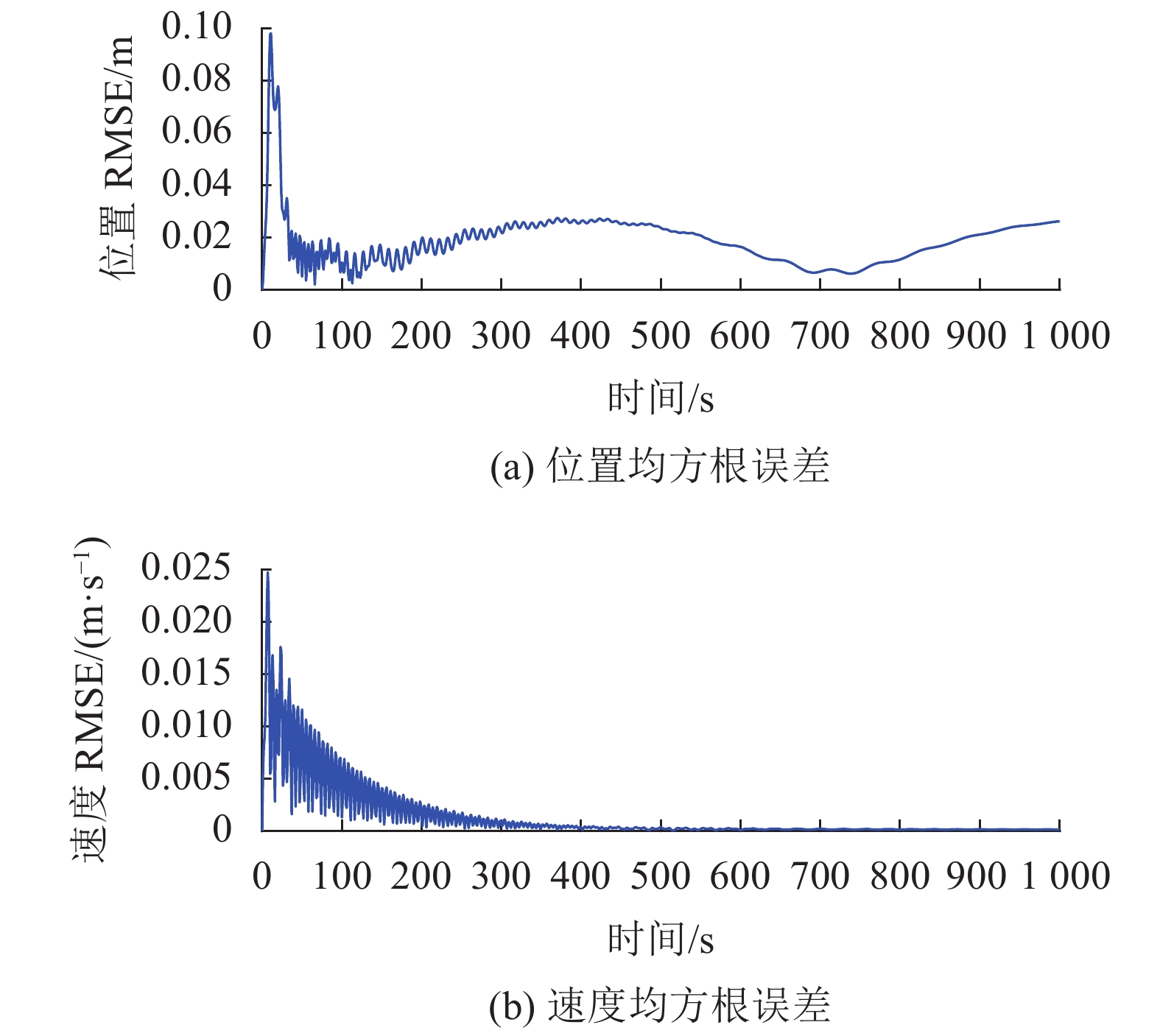
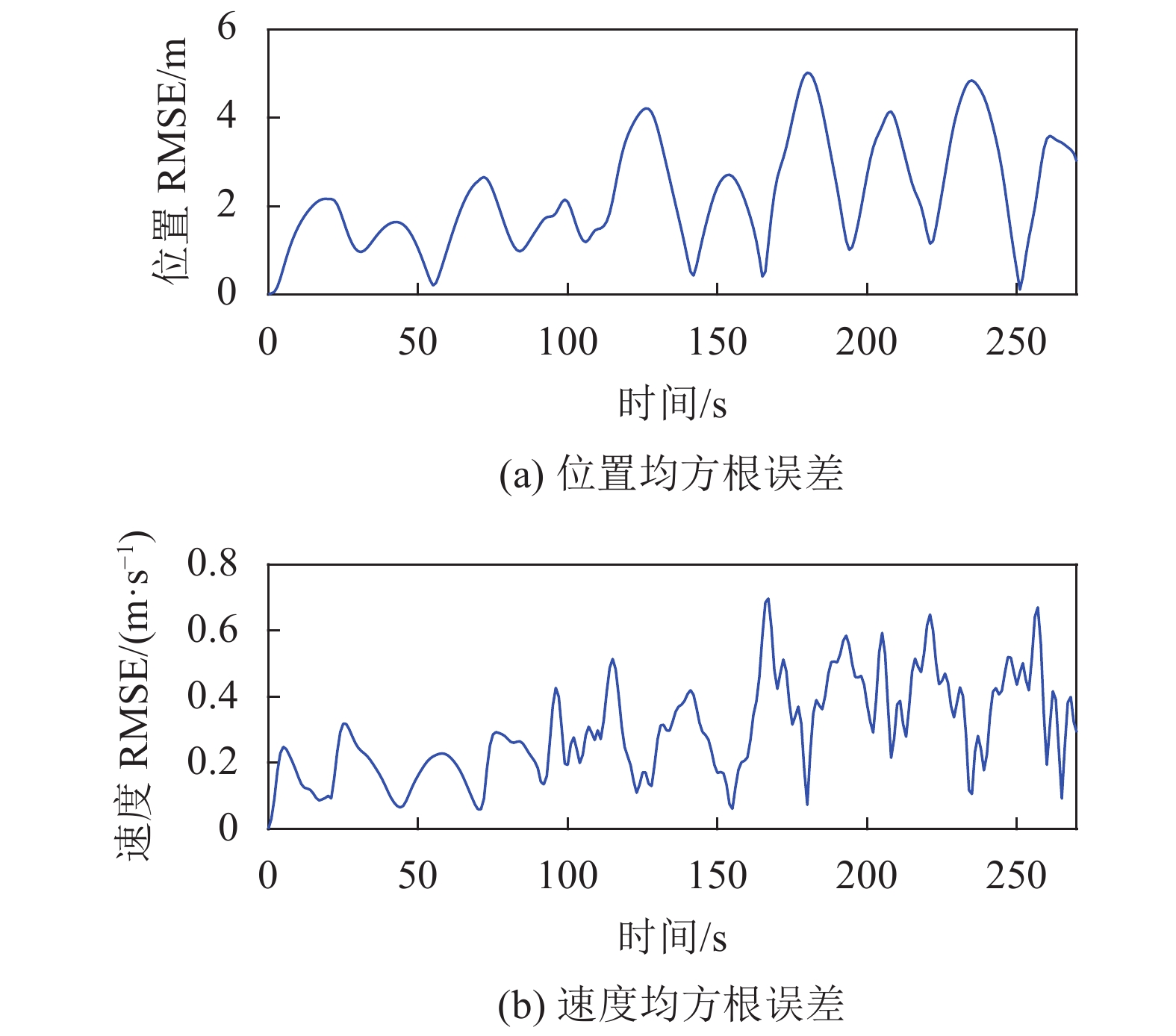
为进一步分析无人机接入虚假卫星信号之后跟踪欺骗轨迹的效果，本文以位置和速度均方根误差（root mean square error, RMSE）为指标，即：
$$ {\text{RMS}}{{\text{E}}_r} = \sqrt {{{({r_x} - \bar r_x^{\rm s})}^2}{\text{ + }}{{({r_y} - \bar r_y^{\rm s})}^2}{\text{ + }}{{({r_{{\textit{z}}}} - \bar r_{{\textit{z}}}^{\rm s})}^2}} \text{，} $$ $$ {\text{RMS}}{{\text{E}}_v} = \sqrt {{{({v_x} - \bar v_x^{\rm s})}^2}{\text{ + }}{{({v_y} - \bar v_y^{\rm s})}^2}{\text{ + }}{{({v_{{\textit{z}}}} - \bar v_{{\textit{z}}}^{\rm s})}^2}} 。 $$ 其中，
$ {\text{RMS}}{{\text{E}}_r} $ 、$ {\text{RMS}}{{\text{E}}_v} $ 分别为位置均方根误差和速度均方根误差。图17和18分别描述了当欺骗轨迹是曲线或折线类型时无人机在整个欺骗过程中RMSE的变化。
图 17 跟踪曲线轨迹时无人机欺骗过程中RMSE变化趋势Fig. 17 RMSE trend diagram during UAV spoofing when tracking curve trajectory下载:
全尺寸图片
图 18 跟踪折线轨迹时无人机欺骗过程中RMSE变化趋势Fig. 18 RMSE trend diagram during UAV spoofing when tracking line trajectory下载:
全尺寸图片
从图17和18可以看出，位置抖动偏差小于5 m，速度RMSE的最大值仅为0.7 m/s，说明以位置和速度RMSE为评价指标，利用逐点偏移式卫星导航欺骗干扰方法跟踪曲线轨迹的欺骗效果要明显高于跟踪折线性，但都能保证无人机在整个欺骗过程中飞行稳定性好，运动状态平缓。
5. 无人机欺骗试验
本文利用卫星信号接收器、卫星信号模拟器和功率放大器的集成箱，以及信号发射器，搭建欺骗验证原理样机（图19），并进行无人机欺骗试验，以验证基于逐点偏移的无人机卫星导航欺骗方法的有效性和正确性。
图 19 欺骗验证原理样机的设备Fig. 19 Equipment of spoofing verification principle prototype下载:
全尺寸图片
先将无人机置于室外空旷环境，开机后起飞至一定高度，保持悬停状态（前期经过大量实验发现，当无人机无法接收到卫星信号时会停止飞行动作而保持悬停状态）。选定目标欺骗偏移的位置区域，利用欺骗验证原理样机向无人机发送虚假卫星信号，测试并记录实验结果。
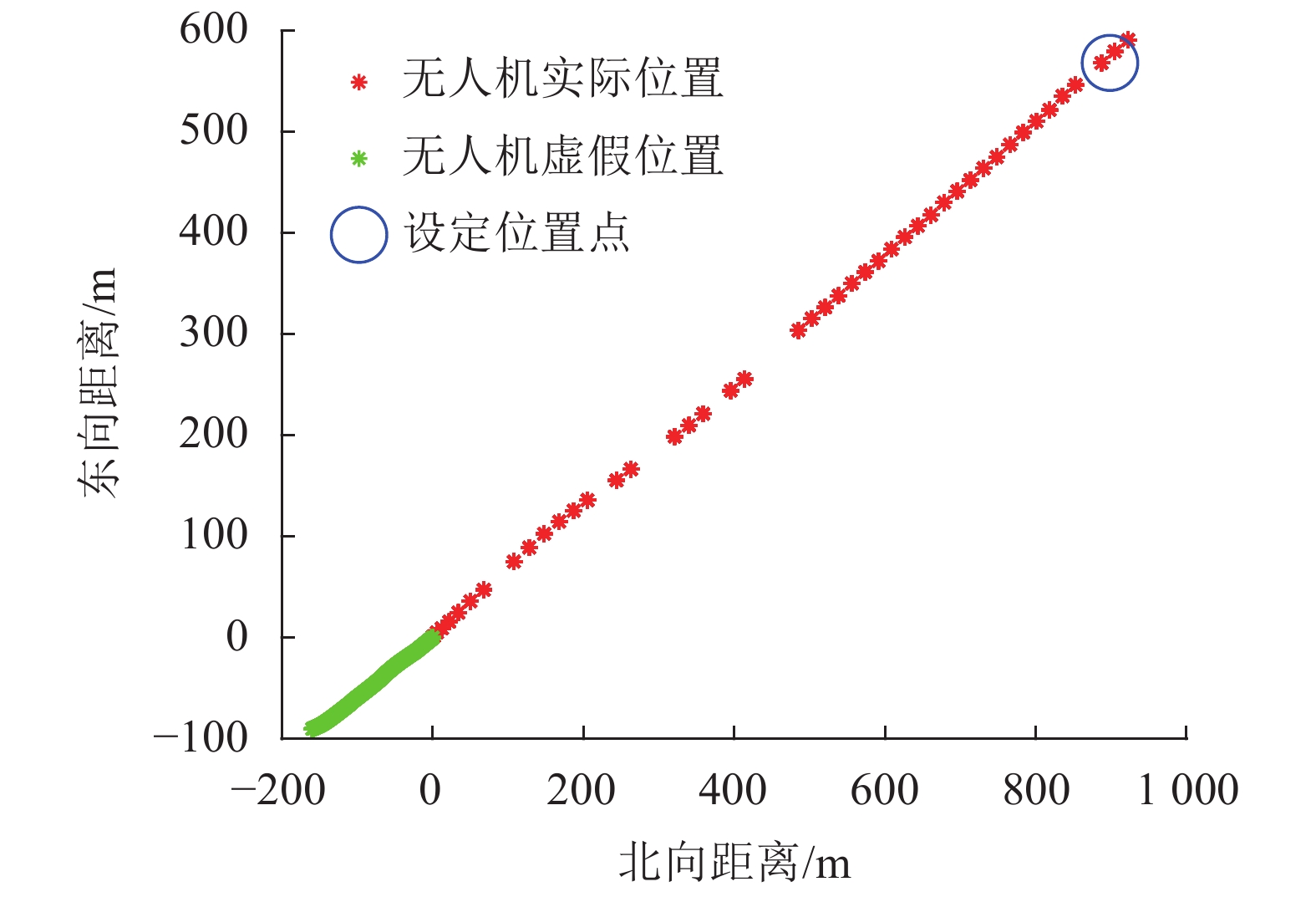
图20给出了利用虚假卫星信号欺骗无人机的效果图。从图20中可以看出，无人机在虚假卫星信号的诱导下慢慢地靠近指定的目标欺骗偏移位置区域，而无人机的虚假位置信息是虚假卫星信号的解算结果，这说明虽然无人机的实际位置已经发生了偏移，但是其卫星导航的输出结果仍在悬停点附近徘徊，进而说明了该欺骗对于无人机而言是无意识的，达到了隐蔽性效果。
图 20 利用虚假卫星信号欺骗无人机的效果Fig. 20 Diagram of spoofing UAV effect with false satellite signals下载:
全尺寸图片
进一步地，根据无人机欺骗算法的原理可知图20所示欺骗效果的产生是因为，虚假卫星信号虽然会一直定位在悬停点附近，但是会存在偏差。无人机的内部飞行控制器会产生控制力矩来削弱这种偏差，然而这种控制力矩不是作用在无人机虚假位置点上的，而是作用在无人机的实际位置上，产生迫使无人机跟踪设定的目标位置偏移点的控制力矩，这一结果与本文基于逐点拉偏式卫星导航欺骗干扰算法原理是一致的。
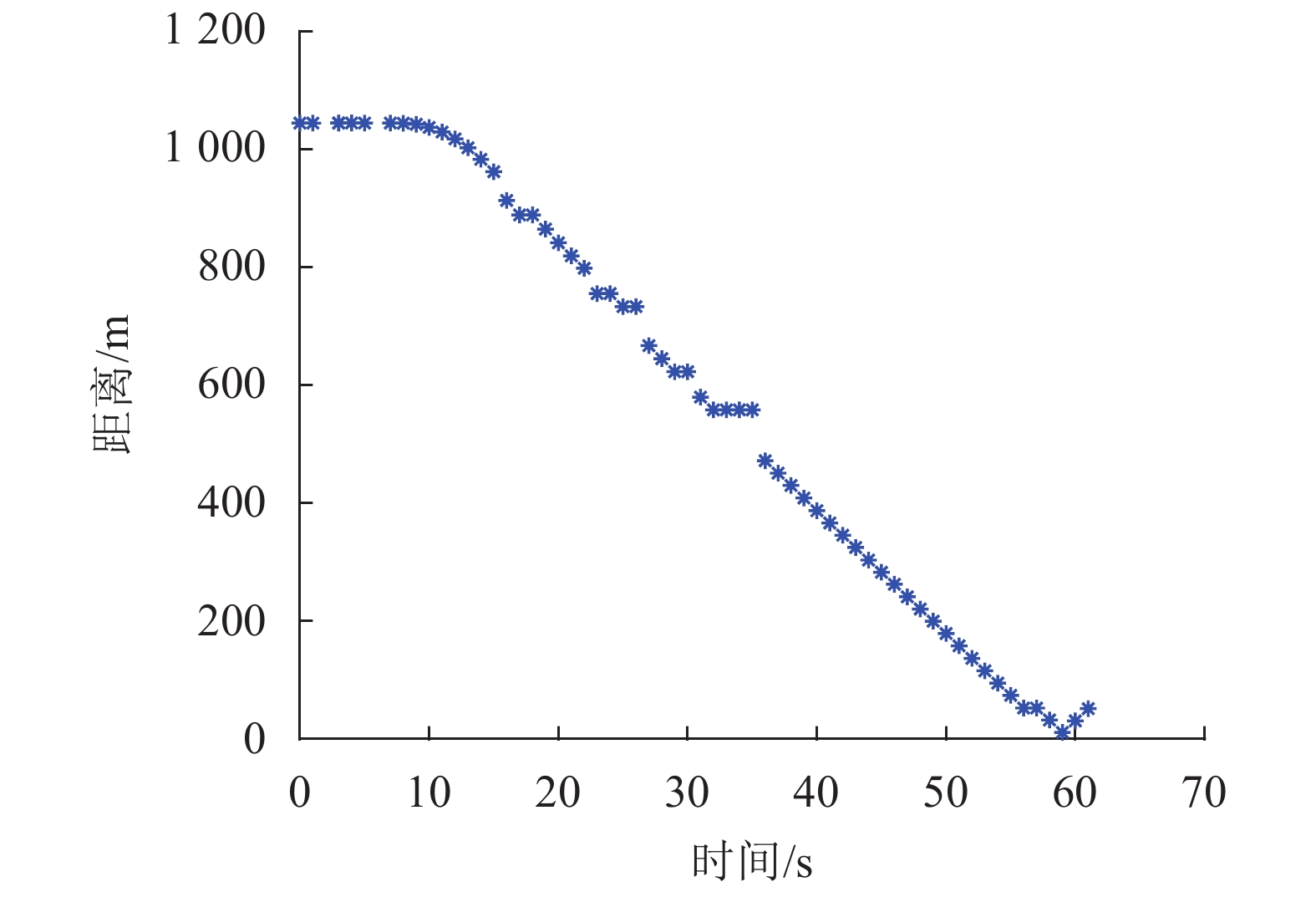
图21给出了欺骗过程中无人机实际位置与设定的目标位置偏移点之间距离随时间变化情况。从图21中可以看出，无人机在虚假卫星信号的诱导下不仅在缓慢地靠近设定的目标位置偏移点，而且能够实现精确地定点偏移，即无人机最终的实际位置点最终会到达期望目标偏移点。
图 21 无人机实际位置与设定的目标位置偏移点随时间的变化情况Fig. 21 Diagram of deviation point between UAV real position and target position changes with time下载:
全尺寸图片
6. 结 论
本文研究一种基于逐点拉偏式卫星导航欺骗方法，该方法将整个无人机欺骗过程看作是单步位置欺骗拉偏的时间迭代过程，且在每一次单步位置欺骗过程中，利用真实控制输入量、原始控制输入量及无人机的运动学模型，设计虚假的GNSS信号使得无人机的位置发生定点欺骗偏移的效果。通过仿真实验分析，无论是跟踪曲线轨迹还是折线轨迹，利用逐点偏移式卫星导航欺骗干扰方法施加虚假的GNSS信号，都能使得无人机跟踪欺骗目标点，达到位置偏移的效果，同时无人机GNSS/INS组合导航滤波器输出的估计状态会绕着原定欺骗目标点运行，达到卫星导航欺骗效果。同时无人机欺骗试验也能取得相同的效果，试验结果可用于探索建立卫星干扰监测与防护体系，为中国北斗卫星导航应用安全与产业化及后续全球系统建设提供技术支撑。
-
图 1 无人机导航和控制反馈闭环回路图
Fig. 1 Diagram of UAV navigation and control feedback closed loop
下载:
全尺寸图片
图 2 k时刻无人机的飞行状态信息图
Fig. 2 Diagram of UAV flight staus information at time k
下载:
全尺寸图片
图 3 k时刻无人机的欺骗控制效果图
Fig. 3 Diagram of UAV soppfing control effect at time k
下载:
全尺寸图片
图 4 生成虚假卫星信号的加速度信息效果图
Fig. 4 Diagram of acceleration information effect for generating false satellite signals
下载:
全尺寸图片
图 5 无人机被欺骗后滤波估计定位效果图
Fig. 5 Diagram of filtering UAV estimated position after being spoofed
下载:
全尺寸图片
图 6 无人机被欺骗后产生靠近目标点控制效果图
Fig. 6 Diagram of generating control near the target point after UAV being spoofed
下载:
全尺寸图片
图 7 将控制效果施加无人机真实位置点上效果图
Fig. 7 Diagram of applying the control effect to the real UAV position point
下载:
全尺寸图片
图 8 无人机位置欺骗的结构设计框图
Fig. 8 Diagram of applying the control effect to the real UAV position point
下载:
全尺寸图片
图 9 3维无人机跟踪曲线轨迹的欺骗效果图
Fig. 9 Diagram of spoofing effect of three-dimensional UAV tracking curve trajectory
下载:
全尺寸图片
图 10 X和Y方向上的曲线轨迹跟踪欺骗效果图
Fig. 10 Diagram of tracking curve trajectory spoofing effect in X and Y directions
下载:
全尺寸图片
图 11 X和Z方向上的曲线轨迹跟踪欺骗效果图
Fig. 11 Diagram of tracking curve trajectory spoofing effect in X and Z directions
下载:
全尺寸图片
图 12 Y和Z方向上的曲线轨迹跟踪欺骗效果图
Fig. 12 Diagram of tracking curve trajectory spoofing effect in Y and Z directions
下载:
全尺寸图片
图 13 3维无人机跟踪折线轨迹的欺骗效果图
Fig. 13 Diagram of spoofing effect of three-dimensional UAV tracking line trajectory
下载:
全尺寸图片
图 14 X和Y方向上的折线轨迹跟踪欺骗效果图
Fig. 14 Diagram of tracking line trajectory spoofing effect in X and Y directions
下载:
全尺寸图片
图 15 X和Z方向上的折线轨迹跟踪欺骗效果图
Fig. 15 Diagram of tracking line trajectory spoofing effect in X and Z directions
下载:
全尺寸图片
图 16 Y和Z方向上的折线轨迹跟踪欺骗效果图
Fig. 16 Diagram of tracking line trajectory spoofing effect in Y and Z directions
下载:
全尺寸图片
图 17 跟踪曲线轨迹时无人机欺骗过程中RMSE变化趋势
Fig. 17 RMSE trend diagram during UAV spoofing when tracking curve trajectory
下载:
全尺寸图片
图 18 跟踪折线轨迹时无人机欺骗过程中RMSE变化趋势
Fig. 18 RMSE trend diagram during UAV spoofing when tracking line trajectory
下载:
全尺寸图片
图 19 欺骗验证原理样机的设备
Fig. 19 Equipment of spoofing verification principle prototype
下载:
全尺寸图片
图 20 利用虚假卫星信号欺骗无人机的效果
Fig. 20 Diagram of spoofing UAV effect with false satellite signals
下载:
全尺寸图片
图 21 无人机实际位置与设定的目标位置偏移点随时间的变化情况
Fig. 21 Diagram of deviation point between UAV real position and target position changes with time
下载:
全尺寸图片
-
[1] Khan S K,Naseem U,Siraj H,et al.The role of unmanned aerial vehicles and mmWave in 5G:Recent advances and challenges[J].Transactions on Emerging Telecommunications Technologies,2021,32(7):1–18. doi: 10.1002/ett.4241 [2] Shin H,Lee J,Shim D H,et al.Design of a virtual fighter pilot and simulation environment for unmanned combat aerial vehicles[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2017:1027. [3] Jeong S,You K,Seok D.Hazardous flight region prediction for a small UAV operated in an urban area using a deep neural network[J].Aerospace Science and Technology,2021,118:107060. doi: 10.1016/j.ast.2021.107060 [4] Ladig R,Paul H,Miyazaki R,et al.Aerial manipulation using multirotor UAV:A review from the aspect of operating space and force[J].Journal of Robotics and Mechatronics,2021,33(2):196–204. doi: 10.20965/jrm.2021.p0196 [5] Mugala S,Okellod,Serugunda J.Unmanned aerial vehicles:Opportunities for developing countries and challenges[C]//Proceedings of the 2020 IST–Africa Conference.Kampala:IEEE,2020:1–10. [6] Childs S J.Developing nations,drones and deterrence:Unmanned aerial vehicles and small nuclear Powers[J].Comparative Strategy,2021,40(1):1–17. doi: 10.1080/01495933.2021.1853431 [7] Chang Yuanzhi,Wang Yongqing,Shen Yuyao,et al.A new fuzzy strong tracking cubature Kalman filter for INS/GNSS[J].GPS Solutions,2021,25(3):1–15. doi: 10.1007/s10291-021-01148-5 [8] Hu Xiao,Olesen D,Knudsen P.Toward high-quality magnetic data survey using UAV:Development of a magnetic-isolated vision-based positioning system[J].GPS Solutions,2021,25(1):1–17. doi: 10.1007/s10291-020-01076-w [9] Sharifi–Tehrani O,Sabahi M F,Danaee M R.GNSS jamming detection of UAV ground control station using random matrix theory[J].ICT Express,2021,7(2):239–243. doi: 10.1016/j.icte.2020.10.001 [10] 赫永磊,李冬,王肖飞.电子对抗手段干扰无人机GPS/INS导航系统效能分析[J].舰船电子工程,2020,40(12):44–47. doi: 10.3969/j.issn.1672-9730.2020.12.010 He Yonglei,Li Dong,Wang Xiaofei.Effectiveness analysis of electronic countermeasures jamming UAV GPS/INS navigation system[J].Ship Electronic Engineering,2020,40(12):44–47 doi: 10.3969/j.issn.1672-9730.2020.12.010 [11] Li Junzhi,Zhu Xiangwei,Ouyang Mingjun,et al.GNSS spoofing jamming detection based on generative adversarial network[J].IEEE Sensors Journal,2021,21(20):22823–22832. doi: 10.1109/JSEN.2021.3105404 [12] Huang Jie,Lo Presti L,Motella B,et al.GNSS spoofing detection:Theoretical analysis and performance of the Ratio Test metric in open sky[J].ICT Express,2016,2(1):37–40. doi: 10.1016/j.icte.2016.02.006 [13] 万有达,马鹏程,聂俊伟,等.基于对固定目标保护的多站转发式欺骗干扰研究[J].全球定位系统,2016,41(1):60–65. doi: 10.13442/j.gnss.1008-9268.2016.01.011 Wan Youda,Ma Pengcheng,Nie Junwei,et al.Study of multi-station retransmission spoofing methods based on protection of fixed target[J].GNSS World of China,2016,41(1):60–65 doi: 10.13442/j.gnss.1008-9268.2016.01.011 [14] Hartmann K,Giles K.UAV exploitation:A new domain for cyber power[C]//Proceedings of the 2016 8th International Conference on Cyber Conflict(CyCon).Tallinn:IEEE,2016:205–221. [15] 乔柳源.伊朗“捕获”美国RQ–170无人机行动中的电子对抗技术分析[J].数字通信世界,2020(5):108. [16] Farnaz F,Julian B E.Iran says it captured American drone,to U.S.denials[J].Wall Street Journal Eastern Edition,2012,260(135):10. [17] Psiaki M L,Powell S P,O’Hanlon B W.GNSS spoofing detection using high-frequency antenna motion and carrier-phase data[C]//Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation.Nashville:ION,2013:2949–2991. [18] Shepard D P,Bhatti J A,Humphreys T E,et al.Evaluation of smart grid and civilian UAV vulnerability to GPS spoofing attacks[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation.Nashville:ION,2012:3591–3605. [19] Broumandan A,Jafarnia–Jahromi A,Lachapelle G.Spoofing detection,classification and cancelation(SDCC) receiver architecture for a moving GNSS receiver[J].GPS Solutions,2015,19(3):475–487. doi: 10.1007/s10291-014-0407-3 [20] Jafarnia Jahromi A,Broumandan A,Nielsen J,et al.GPS spoofer countermeasure effectiveness based on signal strength,noise power,and C/N0 measurements[J].International Journal of Satellite Communications and Networking,2012,30(4):181–191. doi: 10.1002/sat.1012 [21] Bhatti J A.Sensor deception detection and radio-frequency emitter localization[D].Austin:the University of Texas,2015:45–49. [22] Psiaki M L,Humphreys T E.GNSS spoofing and detection[J].Proceedings of the IEEE,2016,104(6):1258–1270. doi: 10.1109/JPROC.2016.2526658 [23] Su Jie,He Jianping,Cheng Peng,et al.A stealthy GPS spoofing strategy for manipulating the trajectory of an unmanned aerial vehicle[J].IFAC-PapersOnLine,2016,49(22):291–296. doi: 10.1016/j.ifacol.2016.10.412 [24] 张会锁,高关根,寇磊,等.利用轨迹诱导的欺骗式GPS干扰技术研究[J].弹箭与制导学报,2013,33(3):149–152. doi: 10.15892/j.cnki.djzdxb.2013.03.008 Zhang Huisuo,Gao Guangen,Kou Lei,et al.Deceptive jamming technology of GPS based on the track induction method[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(3):149–152 doi: 10.15892/j.cnki.djzdxb.2013.03.008 [25] 王文益,陈晨.配备GPS/INS组合导航系统的无人机诱捕方法[J].兵器装备工程学报,2020,41(11):212–217. doi: 10.11809/bqzbgcxb2020.11.039 Wang Wenyi,Chen Chen.Method of trapping UAV equipped with GPS/INS integrated navigation system[J].Journal of Ordnance Equipment Engineering,2020,41(11):212–217 doi: 10.11809/bqzbgcxb2020.11.039 [26] 李畅,王旭东.基于轨迹欺骗的无人机GPS/INS复合导航系统干扰技术[J].南京航空航天大学学报,2017,49(3):420–427. doi: 10.16356/j.1005-2615.2017.03.016 Li Chang,Wang Xudong.Jamming of unmanned aerial vehicle with GPS/INS integrated navigation system based on trajectory cheating[J].Journal of Nanjing University of Aeronautics & Astronautics,2017,49(3):420–427 doi: 10.16356/j.1005-2615.2017.03.016
