在自然语言处理领域，问答一直是重要且十分具有挑战性的任务。几年来，随着大规模知识图谱的涌现，基于知识图谱（knowledge base，KB）的问答引起了广泛的关注。

基于知识图谱的问答可以分为单跳问答和多跳问答。单跳问答是指对于一个简单的事实类问题，可以将知识图谱中存在的与问题实体直接相连的独立3元组作为答案。多跳问答指问答系统需要在知识图谱中的多个相关联的3元组之间执行推理才能获得正确答案。现有工作^[1-2]已经在单跳问答上取得了良好的成果，然而在多跳问答上还面临着许多挑战。

随着深度学习的不断发展，大多数多跳知识图谱问答方法采用端到端的方式，即给定问题和知识图谱，通过深度神经网络学习复杂的数据表示和网络参数来预测答案实体。其中，典型的代表就是图神经网络方法^[3-4]。由于知识图谱本身的图结构性质，图神经网络（graph neural networks，GNNs）能够有效地利用知识图谱的图结构信息。基于图神经网络的知识图谱问答通常遵循3个步骤：首先，根据问题从知识图谱中提取多个相关候选子图；然后，利用图神经网络对子图进行编码；最后，将图或节点的表示送入分类器进行判别^[5-6]。

对于1个节点，传统的图神经网络通过消息传递机制聚合邻居信息。1次聚合只能聚合直接相连的1阶邻居信息，而多层图神经网络进行多次聚合后，1个节点可以捕捉到其未直接相连的高阶邻居信息，这是一种全局性的信息。由于多跳问答任务本身的复杂性，现有基于图神经网络的多跳问答方法大多使用多层图神经网络捕捉多阶邻居信息进行推理，而堆叠多个图神经网络层可能会使得整个图的节点特征过于平滑，从而降低节点表示的判别性^[7]。并且与问题最相关的证据通常分布在实体直接相连的邻居中，将1阶邻居和高阶邻居信息融合在一起的做法忽略了邻居的置信度，无法更高效利用知识图谱中的信息。

除图神经网络方法外，显式建模多跳长路径也可以利用知识图谱信息回答多跳问题的方法，即以用户问题中的问题实体为源实体，在知识图谱多个相关联的3元组之间逐跳进行跳转，沿着显式的推理路径找到答案实体。这类方法面临的挑战在于现有许多多跳问答数据集都是<问题，答案>的形式，一般只给出了最终答案作为监督信号，没有给出问题实体到答案实体之间的准确推理路径，因此基于路径推理的多跳问答模型只能接收来自最后1跳推理结果是否正确的反馈，这被称为弱监督问题。He等^[8]认为弱监督问题会限制模型的中间路径推理能力，比如，模型可能进行歧义路径推理，即从错误的推理路径预测出了正确的答案，此时，模型进行的是无效学习，这会造成模型性能的不稳定。

为了解决图神经网络推理存在限制及模型中间路径推理能力不足的问题，本文提出了一种多视图语义推理网络（multi-view semantic reasoning networks，Mv–SRN），该模型通过一个两层图神经网络初始化实体表示，使实体表示包含了整个子图的全局语义信息；考虑到多层图神经网络存在的过平滑问题，在进行逐跳推理时，模型还结合了实体的局部邻居关系语义信息，旨在关注实体最有价值的一节邻居信息，且使局部信息更具判别性，能够缓解上述问题。

在训练数据只有问答对而没有额外的监督信息时，从语义角度上来看，对模型每一跳推理的指导起关键作用的是问题的语义，即怎样有效分解问题，才能够使模型不同跳数的推理关注问题的不同部分。为了更准确地分解问题语义，本文从问题语义构成的均匀性和一致性出发，设计了一种新颖的损失函数以提升分解的质量。

本文的主要贡献如下：

1）设计了一种同时利用局部语义信息和全局语义信息的多视图语义推理网络，缓解了多层图神经网络存在的过平滑问题。

2）基于问题语义构成的均匀性和一致性，设计了一种新颖的损失函数，以提高问题语义分解的有效性，提升了模型的中间路径推理能力，缓解了弱监督问题。

3）本文在3个真实多跳问答数据集MetaQA^[9]、WebQuestionSP^[10]、ComplexWeb–Question1.1^[11]上进行了实验，实验结果证明了本文方法的有效性。

1.   相关工作

1.1   多跳知识图谱问答

基于知识图谱的问答是指根据知识图谱回答自然语言问题，答案通常是知识图谱中的1个或多个实体。与基于无结构的文本数据信息问答相比，基于知识图谱的问答能够利用知识图谱丰富的结构化语义信息和关联知识，从而提高问题系统质量，如今已经广泛应用于智能搜索、推荐系统、智能问答等任务中，在金融、教育、医疗等多个领域体现出重要的应用价值。

基于知识图谱的主流方法主要可以分为两大类——基于语义查询的方法和基于信息检索的方法。前者通过学习一个语义解析模型，将自然语言问题转化逻辑语义表示，再将其转化为可以直接在知识图谱中执行的描述性语言，代表性方法是Berant等^[12]提出的语义解析器和Yih等^[13]提出的分阶段语义生成方法。而后者则通常根据问题从知识图谱中检索出相关子图信息，再分别提取问题和子图的特征或表征成向量，并通过排序模型候选答案，代表性方法是Yao等^[14]提出的信息检索方法。

到目前为止，简单的单跳问答已经得到基本解决，研究人员更多地关注复杂的多跳推理问答。

多跳推理问答的研究重点是如何理解多跳问题的复杂的语义信息、如何高效地利用知识图谱中的结构化关联知识及如何提高基于知识图谱进行长路径推理的能力。大多研究工作使用信息检索方法^[3]进行多跳知识图谱问答，更具体的做法可以分为基于图神经网络的方法^[4]和基于路径推理的方法^[8]。

1.2   基于图神经网络的多跳问答

随着图神经网络的快速发展，许多研究利用图神经网络进行实体或关系的表示学习，Jhamtani等^[15]认为结构化推理能共更充分利用知识图谱的图结构性质，并得出可解释的结果，例如推理链或推理子图。进行结构化推理的通常做法是，将节点表示、边的表示作为输入，通过多层图神经网络层进行图结构信息的聚合以得到节点表示，最后送给分类器分类。例如Feng等^[16]将路径级别的消息聚合进实体表示，再结合条件随机场计算候选路径的概率，提出了一种路径级别的图神经网络变体。Vakulenko等^[17]提出一种无监督解析问题的方法并利用置信度得分矩阵进行消息传递以预测每一跳实体的概率。Yadati等^[18]以递归超图表示问题子图，并基于一种关系具体的图卷积神经网络^[19]按超边分类聚合信息以更新实体表示，最后直接对实体打分以选择答案实体。然而，以上方法都存在一个问题，即堆叠图神经网络层数过多会导致节点表示过于平滑，丧失判别性。并且与问题最相关的信息大多分布在实体的1阶邻居范围内，不加以区分地将实体的1阶及高阶信息融合在一起的做法无法有效利用最有价值的证据。

为了利用全局信息，本文使用图神经网络聚合问题相关子图信息以初始化实体表示，为了缓解这种简单聚合高阶邻居信息带来的过平滑问题及更有效地利用实体1阶邻居信息，本文在后续每一跳的推理中都将初始化的实体表示和实体1跳内邻居与问题的相关度共同作为判别依据，提出了一种从全局和局部两种视图的语义共同进行推理的方法。

1.3   基于路径推理的多跳问答

多跳知识图谱问答的另一种常见做法是显式推理中间路径。这种方法可以分为两大类，一种是先抽取路径再进行路径选择，另一种是序列化预测关系或实体形成推理路径。

前者通常先从知识图谱中提取多个候选路径，然后将候选路径特征映射到嵌入空间，最后通过打分或排序预测路径和最终答案。早期方法使用路径排序算法提取路径，这些方法通过随机游走抽取路径，存在的问题是抽取路径过程与输入问答对无关，会引入大量噪声。Qin等^[20]通过门控循环单元（gate recurrent unit，GRU）和注意力机制（attention mechanism）编码问题，根据问题的语义信息进行剪枝，使用深度优先搜索算法得出的最佳的路径空间。

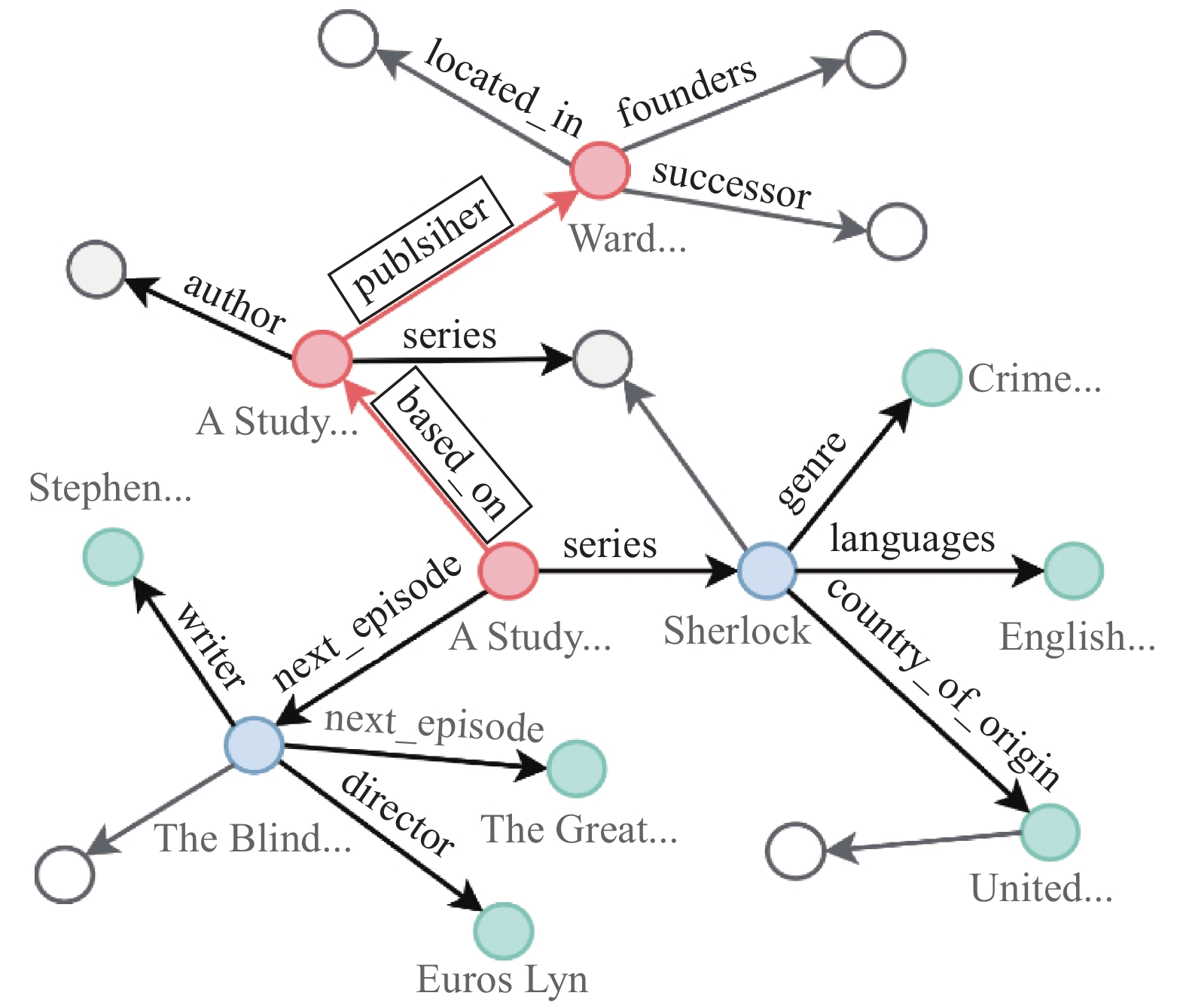
后者序列化预测关系路径的例子如图1所示，对于问题 “Who published the novel adapted into A Study in Pink”，问答模型从问题中的实体“A Study in Pink”出发，沿着 <A Study in Pink, based on, A Study in Scarlet>，<A Study in Scarlet，publisher，Ward Lock & Co> 推理得出答案“Ward Lock & Co”。

图  1  多跳问答实例

Fig.  1  Example of multi-hop question answering

下载: 全尺寸图片

而后者的典型方法是将多跳推理问答任务表述为强化学习（reinforcement learning，RL）问题，将推理过程看作马尔可夫决策（markov decision process，MDP）过程，模型作为一个基于策略的智能体，推理时的状态通常用当前选择的实体和问题表示，动作空间通常用当前实体相连的关系集，推理目标是采取最佳决策顺序（关系边的选择）以最大化预期奖励（到达正确的答案节点）。代表性的方法有Das等^[21]提出的神经强化学习方法、Xiong等^[22]提出的基于强化学习的多跳关系推理框架、Qiu等^[23]提出的结合注意力机制和强化学习的逐跳推理网络。然而，由于数据集缺乏中间路径监督信息，基于强化学习问答严重依赖最后1跳决策的奖励，即推理出的答案实体是否正确，该类方法存在的问题是没有考虑中间决策过程中每一步反馈的即时奖励，这可能会使模型学习到错误的决策顺序，而数据集的弱监督问题使设计有效的中间决策奖励方式十分困难。类似地，其他非强化学习的序列化预测关系路径的模型也是通过最后一跳预测答案的损失来学习，同样面临弱监督问题。

本文推理过程遵循后者的思路，将路径推理过程视为序列化预测路径的过程，为了提升模型中间路径推理能力，本文着眼于问题语义构成的均匀性和一致性，设计了一种的新颖的损失函数，通过使模型每一跳更精准地关注问题不同部分来缓解中间路径缺乏有效的指导问题。

2.   问题定义

知识图谱定义为 ${g} = \left( {\mathcal{E},\mathcal{R},\mathcal{K}} \right)$ ，其中， $\mathcal{E}$ 为实体集合， $\mathcal{R}$ 为关系集合， $ \mathcal{K} $ 为3元组集合。 ${e}{{'}}$ 表示一个3元组的头实体， $ {r} $ 表示关系， $ {e} $ 表示尾实体。 $\mathcal{K}= < {e}{{'}},{r},{e} >$ ； ${e}',{e} \in \mathcal{E}$ ； ${r} \in \mathcal{R}$ 。本文用于推理的知识图谱是问题相关子图而非全部知识图谱，关系集合包含关系本身和关系的逆关系。本文定义实体 ${{e}}$ 邻居实体 ${{e}}'$ 的出边和入边所在的3元组，表示为 ${\mathcal{N}}_{{e}}=\left\{{{e}}{{'}},{r},{e}\in {{g}}\right\}$ 。

给定知识图谱 ${g}$ 和问句 ${\boldsymbol{q}}=\left\{w_1, w_2, \cdots, w_l\right\}$ （ $l$ 是问题长度）及问题中提及的实体 ${e}_{\mathrm{qu}} \in \mathcal{E} $ ，多跳知识图谱问答系统从问题实体 ${e}_{\mathrm{qu}} $ 出发，通过推理在 ${g}$ 中找出答案实体集合，正确的答案实体集合为 $\mathcal{A}_{\mathrm{qu}} \in \mathcal{E} $ 。

3.   方法描述

本文方法总体结构如图2所示，模型可以划分为3个模块：全局初始化模块、问题分解模块、推理模块。

图  2  Mv–SRN结构图

Fig.  2  Structure of Mv–SRN

下载: 全尺寸图片

给定一个问题和对应的知识图谱子图，全局初始化模块通过两层图神经网络对子图中的实体进行初始化，使实体表示包含一定程度的全局信息。问题分解模块将根据预先设定的推理跳数 $n$ ，将问题分解为 $n$ 个子问题表示。推理模块一共进行 $n$ 次实体概率预测，每一跳推理使用对应的子问题表示作为指导，通过消息传递机制聚合实体邻居关系与问题语义的相似度以更新实体的局部表示表示，最后分别使用实体的全局表示和局部表示进行概率预测，得到该跳可能选择的实体的概率分布。

3.1   输入表示

本文使用预训练好的300维预训练Glove（global vectors for word representation）词向量初始化问题表示，并输入到一个单层长短期记忆网络（long short-term memory network，LSTM）获取编码了语义信息的词向量 $ {\left\{{{\boldsymbol{h}}}_{j}\right\}}_{j=1}^{l}，{{\boldsymbol{h}}}_{j}\in {\mathbb{R}}^{d} $ ， $l$ 为问题长度， $ d $ 为向量维度。

因为本文基于知识图谱关系语义和问题语义进行推理，因此关系的初始化为该关系中所有词的词向量平均，记 $\bar{\boldsymbol{r}} \in {\mathbb{R}^d}$ ，由此得到的关系嵌入矩阵记为 ${\boldsymbol{R}}\in {\mathbb{R}}^{d\times \left|\mathcal{R}\right|}$ ， $ \left|\mathcal{R}\right| $ 为关系集大小。

实体有两种视图的表示：实体e的全局表示记为 ${{\boldsymbol{h}}_{e}} \in {\mathbb{R}^d}$ ，所有实体全局嵌入矩阵记为 ${{\boldsymbol{H}}_{\rm{en}}} \in {\mathbb{R}^{d \times \left| \mathcal{E} \right|}}$ ；实体e局部表示记为 $\bar{\boldsymbol{e}} \in {\mathbb{R}^d}$ ，所有实体局部嵌入矩阵记为 ${\boldsymbol{E}} \in {\mathbb{R}^{d \times \left| \mathcal{E} \right|}}$ ， $\left| \mathcal{E} \right| $ 为实体集合的模。

3.2   问题分解模块

在问题分解模块，本文提出了一种新颖的损失函数，从问题分解后的子问题之间应遵从语义均匀性及每个子问题语义都应和原问题语义保持一定的一致性的角度出发，提升了分解的质量。

基于语义进行逐跳推理时，一个很自然的想法是在不同推理步骤关注问题不同部分，因此本文设计了一种问题分解方法，将问题表示 ${\boldsymbol{q}}$ 分解为 $n$ 个子问题表示 $\left\{ {{{\boldsymbol{i}}^{\left( k \right)}}} \right\}_{k = 1}^n$ ， $n$ 为推理跳数。具体地，令 ${\boldsymbol{q}}$ 为问题经过LSTM编码后的词向量 $\left\{ {{{\boldsymbol{h}}_j}} \right\}_{j = 1}^l$ 的平均，即为句子级别的表示。每一跳的子问题表示包含原问题语义信息减去此前所有子问题关注的语义信息后的剩余语义信息，因为之前推理步骤所关注的语义信息在后续推理中是一种冗余。具体分解步骤如下：

式（1）～（3）中： ${{\boldsymbol{W}}^{\left( k \right)}}$ 、 ${{\boldsymbol{W}}_{\text{α}} }$ 、 ${{\boldsymbol{b}}^{\left( k \right)}}$ 、 ${{\boldsymbol{b}}_{\text{α}} } $ 为待学习参数， ${{\boldsymbol{W}}^{\left( k \right)}}、{{\boldsymbol{W}}_{\text{α}} } \in {\mathbb{R}^{d \times d}}$ ， ${{\boldsymbol{b}}^{\left( k \right)}}、{{\boldsymbol{b}}_{\text{α}} } \in {\mathbb{R}^d}$ ； ${{\boldsymbol{i}}^{\left( 0 \right)}}$ 为初始化全零向量； ${{\boldsymbol{i}}^{\left( k \right)}} $ 为第k跳指示向量； $\alpha _j^{\left( k \right)} $ 为第k跳权重向量； ${{\boldsymbol{q}}^{\left( 0 \right)}} ={\boldsymbol{ q}}$ ； ${{\rm{softmax}}}()$ 为归一化指数函数。 $n$ 次迭代上述过程，将问题分解成为 $n$ 个子问题。

3.3   全局初始化模块

He等^[8]提出，由于在问题子图中，中间路径的实体大部分不出现在问题中，与问题相关的语义信息更多体现在关系的语义中，因此关系路径包含的语义信息才是根据问题推导出答案的关键，因此提出一种利用邻居关系表示更新实体表示的方法，但存在只聚合了1阶邻居关系信息，忽略了实体的高阶邻居信息的问题。

本文认为与问题相关的关系并不总是出现在实体相连关系中，有时也出现在其高阶邻居关系中，因此，为了使实体的表示一定程度上包含全局关系信息，本文使用两层图神经网络初始化实体表示。

对实体直接相连的1阶邻居关系信息进行聚合：

对邻居实体信息进行聚合：

式（4）～（5）中， ${\boldsymbol{h}}_{e}^{\left( 0 \right)}$ 为第1次迭代后的实体e的全局表示， $(e',r,e )$ 表示以实体e为尾实体的3元组， $|{\mathcal{N}_{r}}|$ 和 $|{\mathcal{N}_{e}}|$ 分别为邻居关系r和实体e的数量， ${{\boldsymbol{W}}}_{{\rm{t}}}、{{\boldsymbol{W}}}_{{\rm{en}}}\in {\mathbb{R}}^{{{d}}\times {{d}}}$ 为待学习的参数， $\sigma $ 为修正线性单元函数（rectified linear unit，ReLU）函数。经过第1次消息传递之后，子图中的每一个实体都包含了1阶邻居关系信息，因此，第2次通过聚合邻居实体便可以实现间接聚合高阶关系信息，经过两次迭代更新之后，每一个实体表示都包含了一定程度的全局关系信息。

本文并不引入初始化或预训练的实体嵌入，是完全基于知识图谱中关系语义和问题语义推理的方法，这种做法可以降低知识图谱中大量噪音实体本身信息对推理的影响，同时也减少了参数量。

3.4   推理模块

在推理模块，本文通过全局语义信息和局部语义信息的结合来弥补图神经网络因为层数限制而导致的图神经网络所编码的全局信息的全局性不充分问题。

推理模块使用一层消息传递网络聚合邻居信息以更新每一跳实体局部表示，再根据局部表示和实体的全局表示计算该跳选择该实体的概率，得到整个子图实体概率分布 ${\boldsymbol{p}}^{\left( k \right)}$ 。本文在推理过程中并不完全依赖全局信息，而是结合了实体1阶邻居关系的局部语义信息共同进行预测。

模型输入对应推理跳数的子问题表示、上一跳实体分布 ${\boldsymbol{p}}^{\left( {k - 1} \right)}$ 和局部表示 ${\bar{\boldsymbol{e}}^{\left( {k - 1} \right)}}$ ，输出当前跳的 ${\boldsymbol{p}}^{\left( k \right)}$ 和 ${\bar{\boldsymbol{e}}^{\left( k \right)}}$ ，初始实体分布 ${\boldsymbol{p}}^{\left( 0 \right)}$ 是问题实体分布，本文使用归一化实体频率作为问题实体分布，即如果问题子图中有 $m$ 个问题实体，则这些实体的概率为 $\dfrac{1}{m}$ ，其余实体概率为0。

具体推理时，实体局部语义表示是通过消息传递机制聚合1阶邻居关系语义和问题的语义相似度得到的。对于一个实体的所有邻居关系，局部消息 $ {\boldsymbol{m}}_{\rm{local}}^{\left( k \right)} $ 定义如下：

式中， ${{\boldsymbol{W}}_{\rm{RE}}} \in {\mathbb{R}^{d \times d}}$ 是待学习的参数。局部消息根据该实体邻居实体的上一跳分布进行聚合：

根据聚合的消息 ${\widetilde {\boldsymbol{m}}^{\left( k \right)}}$ 动态更新实体局部表示，为了一定程度避免梯度消失问题并加快模型收敛速度，本文在更新实体时引入残差连接：

${\text{FFN}}$ 是单层前馈神经网络，更新后的实体表示具有两部分信息：历史局部语义相似度和该跳局部语义相似度信息，再将该表示送入到一个线性打分函数得到局部视图得分 $score1 $ ：

式中， ${{\boldsymbol{W}}_{\rm{pr}}}$ 、 ${\boldsymbol{b}}_{\rm{pr}}^{\left( k \right)} $ 为待学习的参数， ${{\boldsymbol{W}}_{\rm{pr}}} \in {\mathbb{R}^d}$ ， ${\boldsymbol{b}}_{\rm{pr}}^{\left( k \right)} \in {\mathbb{R}^d}$ 。

为了引入全局信息，直使用全局初始化模块得到的实体全局表示和整个问题表示进行语义匹配，再通过一个线性打分函数得到全局视图得分 $score2 $ ：

式中， ${\boldsymbol{W}}_{\rm{gr}}^{\left( k \right)} $ 、 ${\boldsymbol{ b}}_{\rm{gr}}^{\left( k \right)} $ 为待学习参数， ${\boldsymbol{W}}_{\rm{gr}}^{\left( k \right)} \in {\mathbb{R}^d}$ ， ${\boldsymbol{ b}}_{\rm{gr}}^{\left( k \right)} \in {\mathbb{R}^d}$ 。最后结合两种视图得分共同计算本跳实体概率分布：

3.5   损失函数设计

模型答案预测损失 ${\mathcal{L}_{\rm{f}}} $ 为预测答案实体分布 ${{\boldsymbol{p}}^{\left( n \right)}}$ 和真实答案实体分布 ${\boldsymbol{p}}{\text{*}}$ 的KL散度，采用函数 ${D_{\rm{KL}}}() $ 计算：

此外，为了提升问题分解的质量，本文将问题分解视为无监督任务，引入对比学习（contrastive learning）中常用的损失函数InfoNCE^[24]。受到Wang等^[25]提出的均匀性和一致性两个概念的启发，本文认为，问题分解的目的是使不同推理跳数关注问题的不同部分，即分解整句问题的语义，分解后的语义也应当遵循这两个性质。具体地，一致性是指分解后的子问题语义是原问题语义中的一部分，所有子问题和原问题都遵循一定程度的语义一致性。均匀性是指问题的分解应当倾向使所有子问题的语义信息既互相有差异，又能保留尽可能多的原问题语义信息，子问题之间分布均匀则意味着两两有差异，各自又包含独有信息，从而原问题信息保留充分。对于一个子问题表示来说，本文将问题表示看作该子问题表示的正例样本，将其余子问题表示视为负例样本，本文设计了一个问题分解损失使子问题之间语义分离的同时，一定程度地保持和原问题语义的一致性：

式中： $\mathcal{L}_{\rm{C}} $ 为问题分解损失；分子为每个子问题表示和问题表示的相似度，本文使用余弦相似度计算；分母为该子问题表示和其他子问题表示的相似度之和； $\tau $ 为温度系数超参数，用以调节均匀性和一致性的比例。

最后，本文联合训练问题分解模块和推理模块，模型整体损失 $\mathcal{L} $ 为：

式中， ${\lambda _{\rm{c}}} $ 为控制模型分解损失的超参数， ${\lambda _{\rm{c}}} \in \left( {0,1} \right)$ 。

4.   实验设定

4.1   实验数据集

本文在3个多跳知识问答数据集上进行了实验。

1）WebQSP。WebQuestions^[12]的子集，在其基础上并删除了一些表达有歧义及无清晰意图或答案的问题。WebQSP包含4737个1跳或2跳问题，问题的答案可以在数据子集FreeBase中找到。

2）CWQ。在问句的结构和表达多样性等方面进一步增强了WebQSP，包括类型约束，显隐式的时间约束，聚合操作等等。CWQ共包含34 689个问题及其对应的答案和SPARQL查询。

3）MetaQA。一个电影领域多跳问答数据集，它包含超过40万个电影领域的多跳问题，这些问题有Vanilla、NTM和Audio3个版本。本文使用的是Vanilla版本。Vanilla版本的MetaQA常被用于多跳知识问答推理任务，它除了包含1跳（Meta–1H）、2跳（Meta–2H）和3跳（Meta–3H）3种类型的问答数据，还包含1个知识图谱，其有约135 000个3元组、43 000个实体及9种关系。

本文将数据集划分为两类，一类是以FreeBase为知识图谱的开放领域复杂数据集WebQSP和CWQ，另一类是相对来说更简单的电影领域问答数据集MetaQA。所有数据集的划分和预处理都遵循Saxena等^[26]的工作。预处理工作是给定数据集给出的问题和问题实体，通过对应知识图谱中Andersen等^[27]提出的局部图划分算法，提取问题实体的2跳子图。后续推理在子图上进行。数据集划分为训练集、验证集、测试集，所有的实验都在训练集上进行训练，在验证集上优化参数，在测试集上比较结果。样本数量统计数据如表1所示。

4.2   对比模型

由于两类数据差异较大，现有方法通常面向单独一类数据集，本文在尽量遵循对比模型一致的前提下，选取以下模型进行3个数据集上的实验结果比较。

1）KVMemNN^[28]。一种使用记忆网络存储知识图谱信息，迭代访问记忆模块进行多跳推理的模型。

2）GraphNet^[29]。该模型引入外部文本语料，和知识图谱结合形成异质图，提出一种图卷积神经网络变体，可以在异质图上多跳推理。

3）SGReader^[30]。该模型利用文本预料弥补知识图谱不充分问题，首先从与问题相关的知识图谱子图中抽取实体的知识，然后在嵌入空间中重新表述问题，再利用实体知识抽取文本相关信息，最终从知识图谱和文本中获得预测相似度的信息。

4）TextRay^[31]。该模型使用一种新颖的分解–执行–连接方法来回答复杂的问题。该模型能够使用隐含的监督从问答对中学习简单的查询，从而消除对复杂查询模式的需求。

5）ReifKB^[32]。该模型提出了一种在大规模知识图谱上，基于标签形式的可扩展的概率转移方法。

6）2HR-DR^[33]。该模型提出一种动态关系的两阶段超图推理方法，能够动态关注不同跳数下的不同关系。

7）GlobalGraph^[34]。该模型从节点类型相似度和节点与问题之间的相关性对长距离节点关系进行建模。

8）TransferNet^[35]。该模型提出一个统一的复杂多跳问题问答框架，同时支持标签关系和文本关系。

9）QGG^[36]。该模型提出了一种新的查询图生成方法，从整个知识库开始并逐渐将其缩小到所需的查询图。

10）NSM_+h^[8]、NSM_+p^[8]。该模型提出一种基于知识蒸馏和双向推理显式学习中间路径监督信号的方法。前者表示混合型双向结构，后者表示平行型双向结构。

10）DCRN^[37]。该模型提出一种深度认知推理网络，包括无意识阶段和有意识阶段两个阶段。前者检索信息通过利用候选实体的语义信息从候选实体中获取证据。意识阶段根据检索到的图结构执行顺序推理准确识别答案。

4.3   实施细节和评估标准

本文使用F1和Hit@1（H1）作为评估指标。H1是问答系统的常见指标，计算所有测试样本中模型预测排序最高的答案是正确答案的样本比例。H1衡量的是模型最佳预测答案的准确性，F1分数是是模型精确率和召回率的平均值，衡量的是模型预测所有答案的能力。本文在验证集上进行参数选择，最终确定的超参数如下：在CWQ和WebQSP数据集上，推理跳数为4，批次大小分别为20和40，学习率为0.005，问题分解损失的超参数 ${\lambda _c}$ 设置为0.1。在MetaQA数据集上，Meta–3H推理跳数设定为3，Meta–2H设定为2，Meta–1H为1，批次大小都为80，学习率为0.0 005，问题分解损失的超参数 ${\lambda _c}$ 设置为0.005。所有数据集上问题分解损失的温度系数 $\tau $ 都为0.07。

5.   实验结果分析

本文提出的模型和对比模型在3个数据集上的结果见表2、3。

从表2、3中可以观察到的结论如下：

1）在WebQSP和CWQ数据集上，本文模型在全部指标上超越了对比模型。而在简单的多跳数据集MetaQA上，本文模型结果和对比模型结果相似。其中，本文模型实验结果在Meta–2H上F1达到100%。具体地，相比于在3个数据集上表现都很好的模型NSM_+h，模型在最复杂的数据集CWQ上提升最高，H1和F1各自提升了1.4%和9.5%，在复杂度其次的WebQSP上，H1和F1各提升了0.4%和3.5%。以上数据说明本文模型处理复杂数据集的能力更强，这可能是因为：相比于复杂数据集而言，简单数据集子图中的正确推理路径呈线性结构，且相关推理路径很少，因此，本文全局初始化模块作用不明显；而复杂数据集的正确推理路径可能呈图结构而非线性结构，和问题相关的关系可能更发散地分布在实体的高阶邻居关系中，因此本文模型的全局初始化模块可以发挥更大的作用。这也可以解释本文模型在Meta–1H上的H1与最好的结果差了1.6%，在Meta–2H上却达到100%的原因。Meta–1H的答案实体与问题实体相连，并不需要全局信息辅助推理，因此模型在Meta–1H上表现最差。

2）在所有对比模型中，KV–Mem、GraftNet、SGReader额外使用了文本语料库，而本文模型在仅使用问答对和知识图谱作为数据源的情况下，几乎所有结果都超越了这些模型，证明了本文工作的有效性。

5.1   消融实验

在WebQSP数据集上，本文对全局初始化（global initialization，GL）、问题分解（query decomposition，QD）、问题分解损失（query decomposition loss，QL）进行了进一步的消融实验以验证各模块的有效性，结果见表4。

从表4中可以观察到：

1）所有消融后的实验在两个指标上的结果都比不上原始结果，说明消融的每一个模块都是起作用的。其中效果最差的是去掉全局初始化模块，其次是去掉整个问题分解模块，体现了这两个模块的重要性。

去掉全局初始化模块后，模型只根据实体邻居关系和子问题表示的相似度进行实体选择，忽略了实体高阶邻居关系对实体选择的贡献。实验结果符合本文认为将全局和局部两种视图信息结合起来更有助于推理的假设。而去掉问题分解模块后，模型推理的每一跳都使用整个问题的语义信息作为指导，没有重点关注有效语义部分，实验结果符合本文认为在不同推理跳数应该关注问题不同部分语义的假设。

2）在去掉全局初始化实验中，推理时没有加入全局性得分，但局部性实体表示的更新过程的初始化不再是全0初始化，而是随机初始化，引入了实体初始化参数。这一个实验在测试集上表现是最差的，但在训练集上表现很好，收敛前后的损失都低于其他实验，这说明出现了严重的过拟合。

5.2   参数选择实验

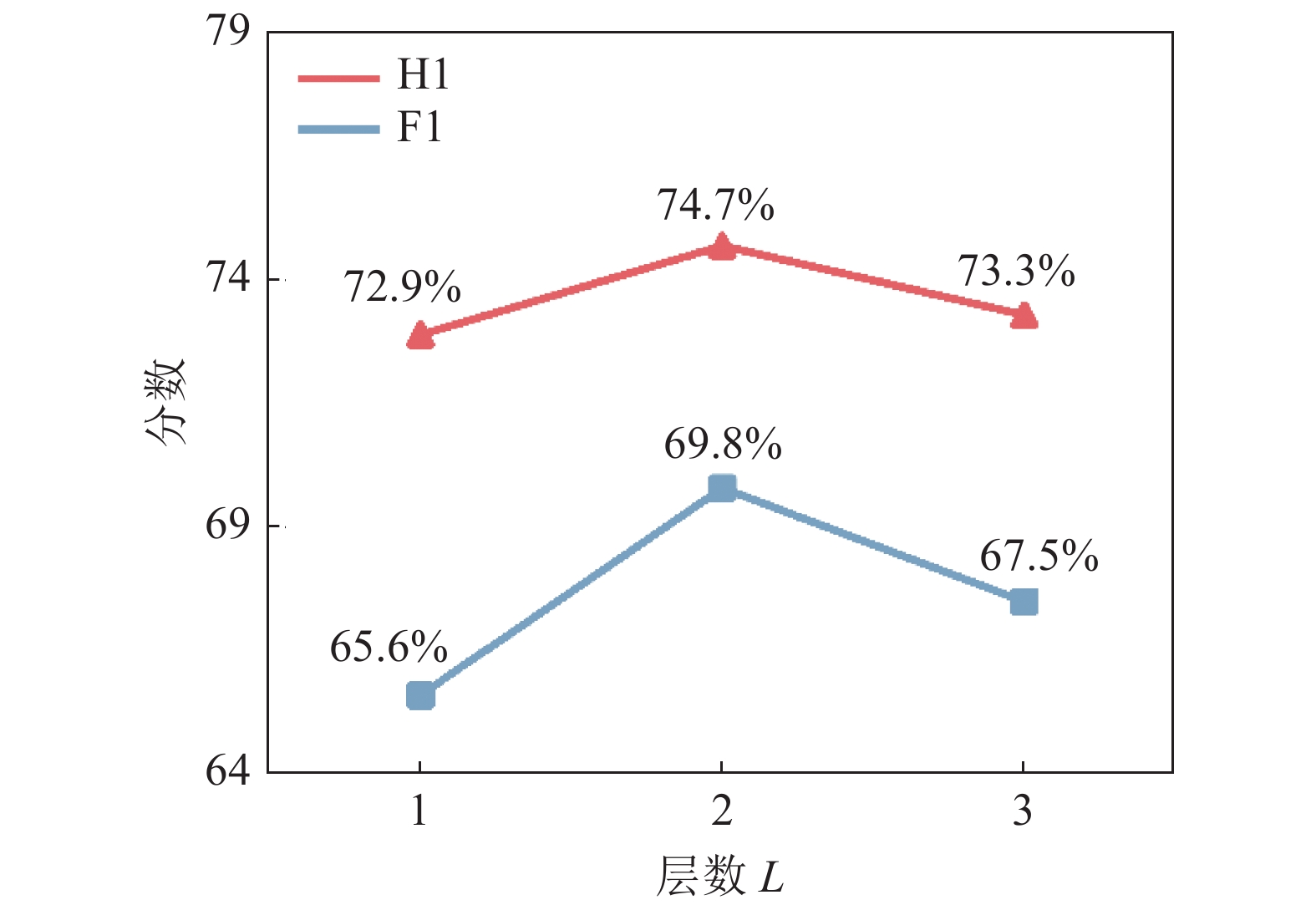
为了研究图神经网络层数带来的影响，在WebQSP数据集上，本文改变了全局初始化模块图神经网络层数进行对比实验，结果如图3所示。

图  3  不同图神经网络层数的实验结果

Fig.  3  Results of different GNNs layers

下载: 全尺寸图片

图3中全局初始化层数 $L = 1$ 时，表示初始化实体时只聚合实体的邻居关系， $L = 2$ 是本文模型的设置， $L = 3$ 时第1层聚合邻居关系，第2层聚合邻居实体，第3层再聚合一次邻居实体。

从图3中可以看到， $L = 1$ 和 $L = 3$ 时模型效果都下降了，其中 $L = 3$ 表现得更差，这说明只聚合1次邻居时，只能捕捉到局部邻居信息；而聚合多次邻居信息时，会存在过平滑问题，导致每个更新的节点表示包含的信息趋于一致；当试图用全局初始化模块捕捉全局信息用于推理时，过于局部性的信息和过平滑的信息都会使模型效果下降。

5.3   问题分解可视化

为了更加直观地分析问题分解损失对分解问题语义的作用，本文对比了Meta–3H的一个测试样本“who starred in the movies whose writers also wrote road to perdition?”在加入问题分解损失前后的问题分解权重 $\alpha _j^{\left( k \right)}$ ，如图4所示，图4（a）为没有加入问题分解损失的权重，图4（b）为是加入之后的权重，图4（c）为问题正确的关系路径。从图4（a）可以看出，模型前两跳关注的词语义权重分布均匀，没有关注相关词，最后1跳有效关注到了“starred”；而图4（b）中，模型后两跳都精确关注到最相关的词，第1跳关注了问题实体。对比两者的表现，可以说明问题分解损失能够有效提升每一跳关注语义的准确性。

图  4  问题分解权重可视化

Fig.  4  Weight visualization of query decomposition

下载: 全尺寸图片

5.4   50%关系缺失测试

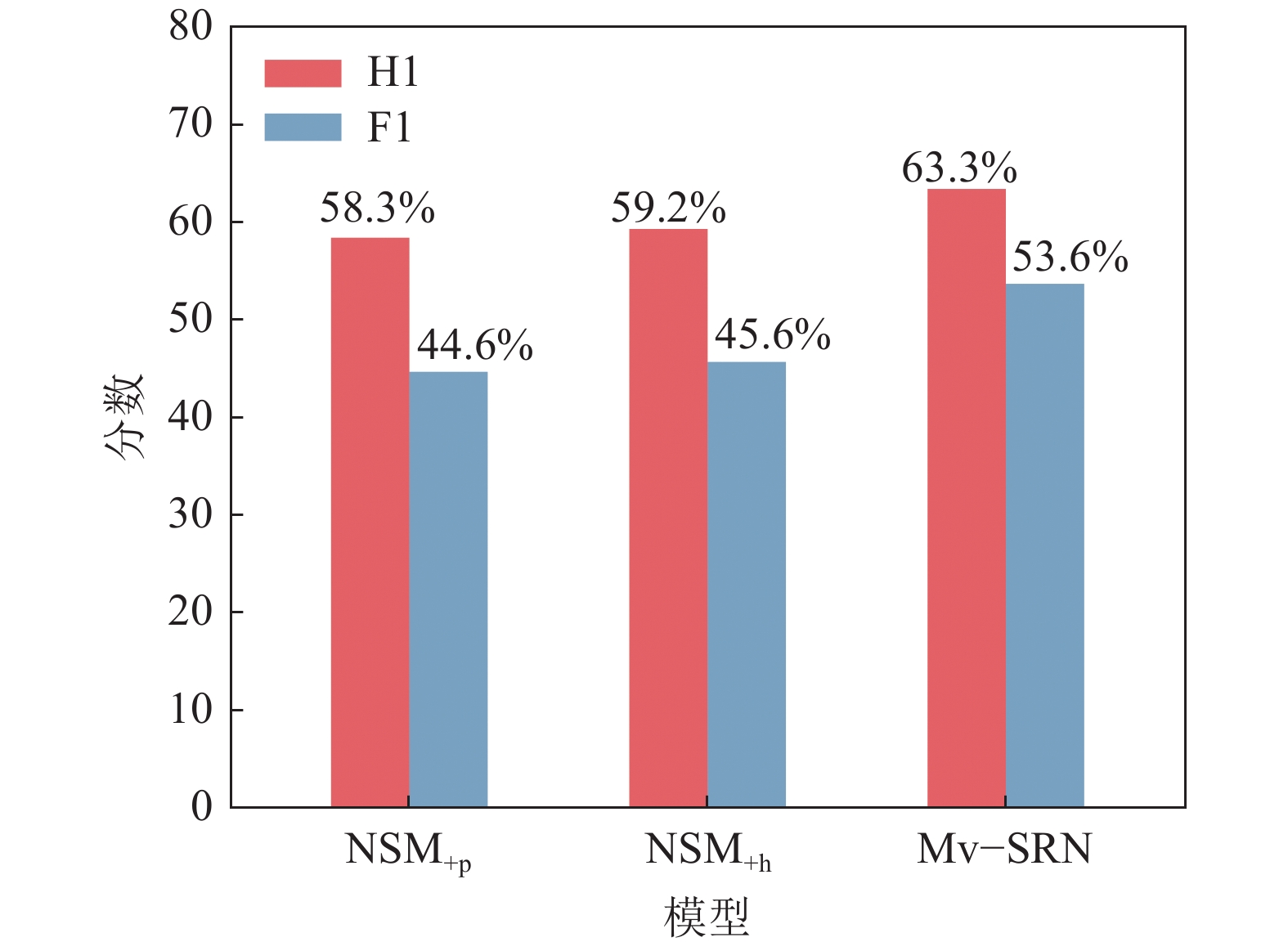
知识图谱本身不完备，存在本来有关系的实体间关系缺失的问题，关系缺失会导致预定义推理跳数的模型在规定跳数内到达不了正确答案实体，也会导致推理需要的跳数比原本多，降低推理性能，增大推理开销。本文基于全局初始化模块捕捉到的全局信息和实体局部关系信息共同进行推理，当局部关系缺失时，模型还可依赖全局信息进行预测，模型每一次推理是将整个子图中的实体作为候选实体，即使关系缺失也可以选择到对应的实体。因此，本文提出的Mv–SRN可缓解知识图谱稀疏性问题。为了验证这个假设，以50%概率随机丢弃数据集WebQSP中的关系以模拟关系缺失的知识图谱，并将提出的Mv–SRN和NSM_+h、NSM_+p在该数据集上进行实验，模型性能指标如图5所示。

图  5  知识图谱50%关系缺失测试结果

Fig.  5  Results on 50% relationship deficiency test of KB

下载: 全尺寸图片

5.5   复杂度分析

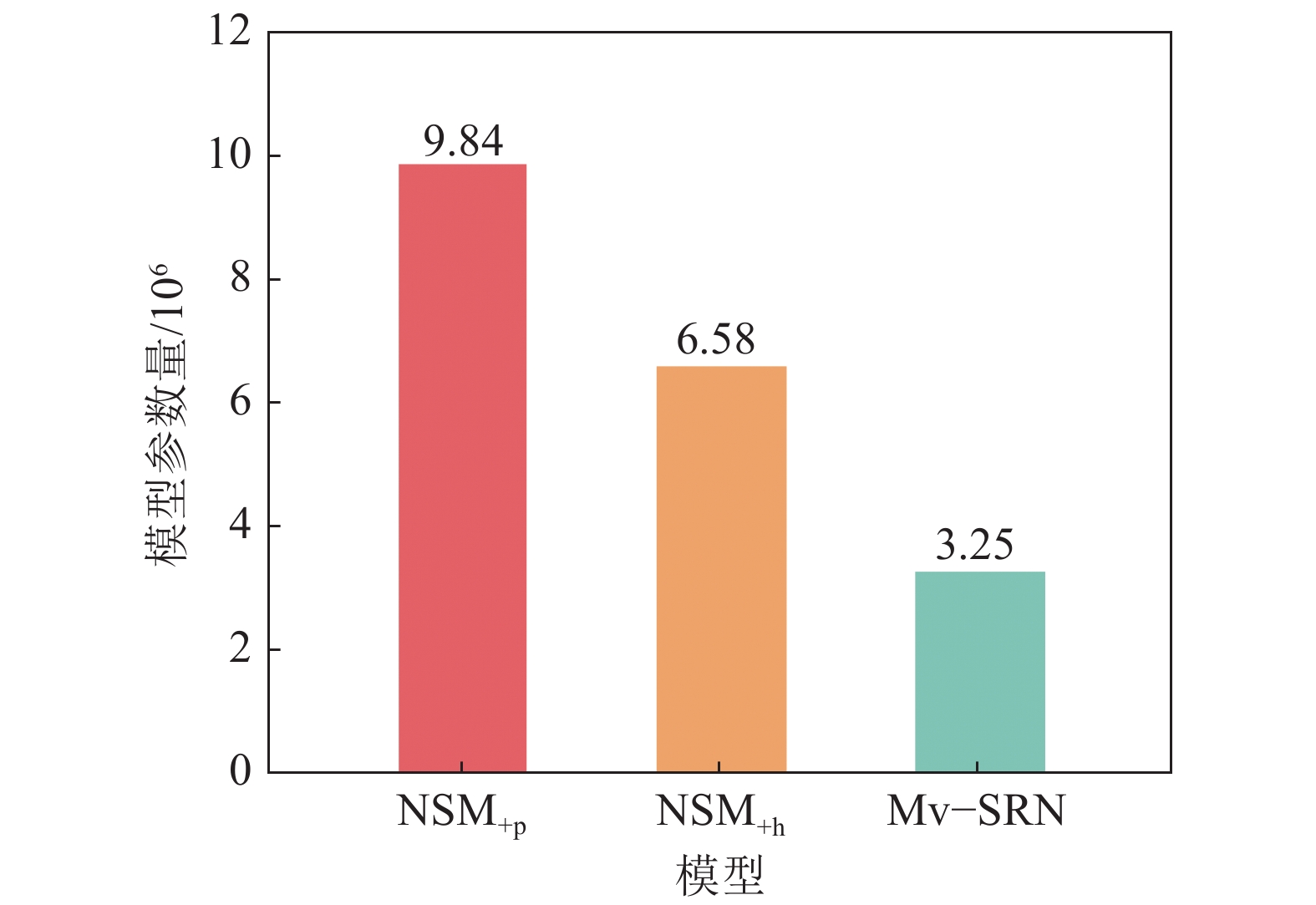
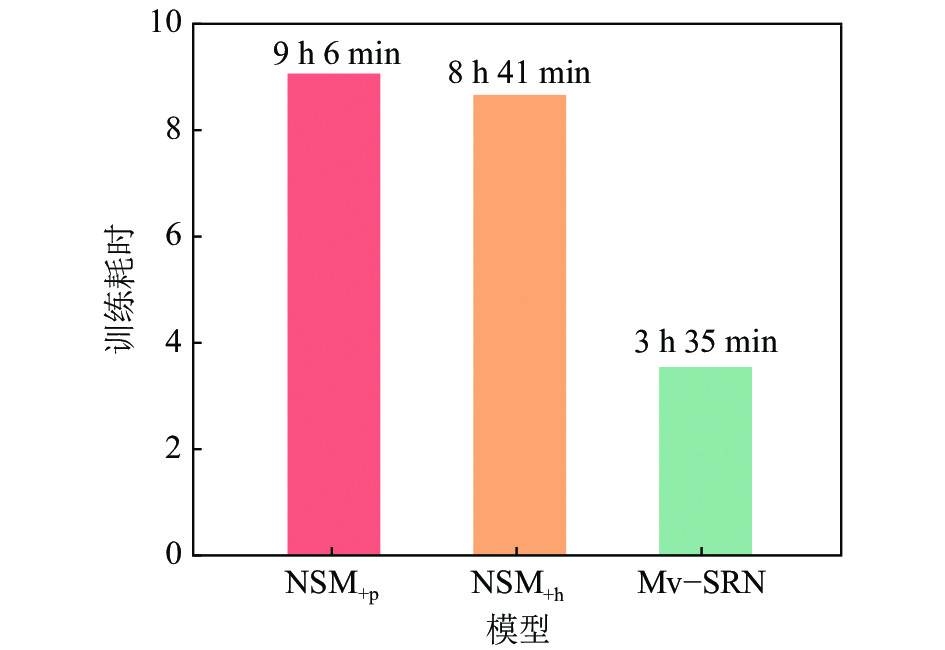
推理模块与提出的Mv–SRN最相似的研究是NSM_+h、NSM_+p，这两个模型在推理时同样对实体邻居关系与问题语义相似度进行消息传递，以此更新实体表示再计算实体分布。NSM_+h、NSM_+p将这个推理过程定义为从问题实体到答案实体的单向推理。本文模型推理过程与之不同的是额外利用了全局信息进行推理。从表2中对比NSM_+h、NSM_+p和本文模型，可以看出，本文模型在复杂数据集WebQSP、CWQ上性能表现更好，在数据集MetaQA上与其他模型表现相似。然而，NSM_+h、 NSM_+p模型结构采用教师学生模型进行知识蒸馏，教师模型是一个双向推理模型，即除了上述的单向推理以外，还额外添加从答案实体推理到问题实体的反向推理过程，目的是根据两个推理过程的分布一致性对齐前后向模型预测的实体分布，以学习有效的中间监督信息，再用以指导学生模型从问题实体开始的单向推理；因此，整个教师学生模型参数量是单向推理模型的3倍左右。此外，NSM_+h、NSM_+p的训练方法是先训练教师模型到收敛后，再训练学生模型；因此，其训练模型所需要的时间也很长。而本文模型只有一个单向推理过程，并且是基于关系的推理，不使用实体本身的嵌入，其参数量和训练时间较小。图6、7是模型参数量大小和训练时间比较结果。如图6、7所示，本文模型参数量和训练组时间远小于NSM_+h、NSM_+p，但达到了与其他模型相似甚至更好的结果（3个模型都在相同环境下运行：GPU型号为RTX A6000–48G，单GPU），说明本文模型在参数量和训练时间上也具有一定优势。

图  6  参数量比较结果

Fig.  6  Comparison results of model size

下载: 全尺寸图片

图  7  训练时间比较结果

Fig.  7  Comparison results of training time

下载: 全尺寸图片

5.6   错误率及案例分析

本文提出的模型在简单数据集MetaQA上的H1和F1都很高，训练收敛后的损失也接近0，但相比于最新的工作^[38]，却没有明显超越。为了研究本文模型在这个数据集上表现不够好的原因，本文对Meta–3H数据集中的测试案例进行了分析——在14 274个测试案例中，对8 115个案例预测正确，而对其余6 159条案例模型输出包括1个或多个答案完全预测错误、部分预测错误和预测的答案都是正确答案但预测不完全3种情况，具体的统计信息见表5。由表5可以看到，大部分情况都是模型预测的答案不完全。表6为这类错误案例中的具体实例，模型预测答案以{实体：概率}形式给出，带星号表示预测为正确答案。

由图6可知，对于Meta–3H数据集来说，模型表现不足较为突出的一个地方在于多答案问题预测不充分。在未来工作中可以考虑如何改进这个问题。此外，观察完全预测错误的样本发现，大部分错误的都是关于询问语言的问题，如“what are the languages spoken in the movies starred by premonition actors”，但关于语言的问题也不乏完全预测正确的样本。模型在部分有关语言的样本上表现如此不好的原因值得探究，未来工作中会从检视数据集本身和问题子图结构来探究该问题。

6.   结　论

本文提出了一种利用知识图谱和问题的全局、局部两种视图语义进行推理的模型Mv–SRN。在推理之前，本文使用两层图神经网络捕捉问题子图全局信息以获得实体的全局表示，在推理过程中计算实体邻居关系和问题的语义相似度并通过消息传递更新实体局部表示，最后基于全局和局部两种视图语义信息的实体表示进行概率预测，以得到每一跳选择实体的分布。在推理过程中，每一跳的推理由问题分解模块得到的子问题表示作为指导，本文从问题语义构成的均匀性和一致性出发，设计了一个新颖的问题分解损失函数以提升问题分解的质量。

未来工作包括以下方面：对于知识图谱，本文模型只利用到其图结构信息和关系的语义信息，没有用到其实体信息，因此，如何结合实体信息提升推理性能是未来的工作之一。此外，自然语言问题包含的信息除了语义信息还有句法结构信息，本文只利用其语义信息，在未来工作中会研究如何有效利用问题的句法结构信息以提升问题分解的质量。最后，本文提出的问题分解损失只使用该问题分解的其他子问题表示作为其中一个子问题表示的负例，受到对比学习使用大量负例的启发，未来工作将尝试如何构造更多的负例以改进问题分解损失的设计。