地下矿山生产中最常使用的方法是房柱法或房柱嗣后充填采矿的方法^[1]，其方法在回采时，通过预留矿柱支撑顶部岩体以保证采场结构的稳定，因此，合理的矿柱尺寸设计是关键。然而，随着浅层矿物资源的逐渐枯竭，矿体开采深度不断增加，资源开发已经逐渐进入埋深超千米的深部开采阶段。此情况下原岩应力水平升高，采场内岩体受开挖扰动影响较大，岩体动力破坏频次和强度均有所上升，冲击地压现象突出^[2]，岩体稳定性更加难以保证，矿柱尺寸参数的合理选择具有更大的挑战。

国内外学者针对矿柱尺寸参数设计进行了大量的研究工作。已有研究表明，矿柱宽度是影响矿柱稳定性的最敏感因素，高度次之，故确定矿柱预留宽度是设计的关键^[3-4]。经过生产实际的不断探索，在矿柱尺寸设计的理论计算方法上，逐步形成了安全系数法^[5]、工程类比方法^[6]、Mathew图法^[7]，以及部分学者利用材料力学和弹塑性力学等^[8]方法对矿柱的稳定性进行分析求解。值得注意的是，上述确定矿柱尺寸参数的理论计算方法是基于静态作用力实现的，忽略了实际动态开挖这一过程。在矿山生产实际中，常以钻爆开挖作为采矿的主要手段，矿体的瞬间崩落、矿柱的快速形成所带来的瞬态加载作用和矿柱动力破坏现象不容忽视^[9]。Esterhuizen等^[10]研究发现，尽管某矿山矿柱具备较高的安全系数，但依然会在没有任何征兆的情况下发生冲击破坏。Li等^[11]的研究也证实矿体回采过程中不能忽视其中的爆破扰动和卸荷扰动动力作用。因此，以一种动态视角研究矿柱的稳定性，并据此形成相应的尺寸设计方法，在应对深部采矿动力灾害防治问题上具有重要的理论意义和工程价值。

针对房柱式开采中确定预留矿柱尺寸参数的理论计算方法展开研究，基于功能转化原理探讨了快速开挖方式下的矿柱应变能的储存和转化特征，并对矿体阶段性分多次开采这一过程进行简化，建议了一种考虑分层爆破扰动作用的矿柱尺寸设计的能量方法。

1.   计算基本理论

1.1   基本假定

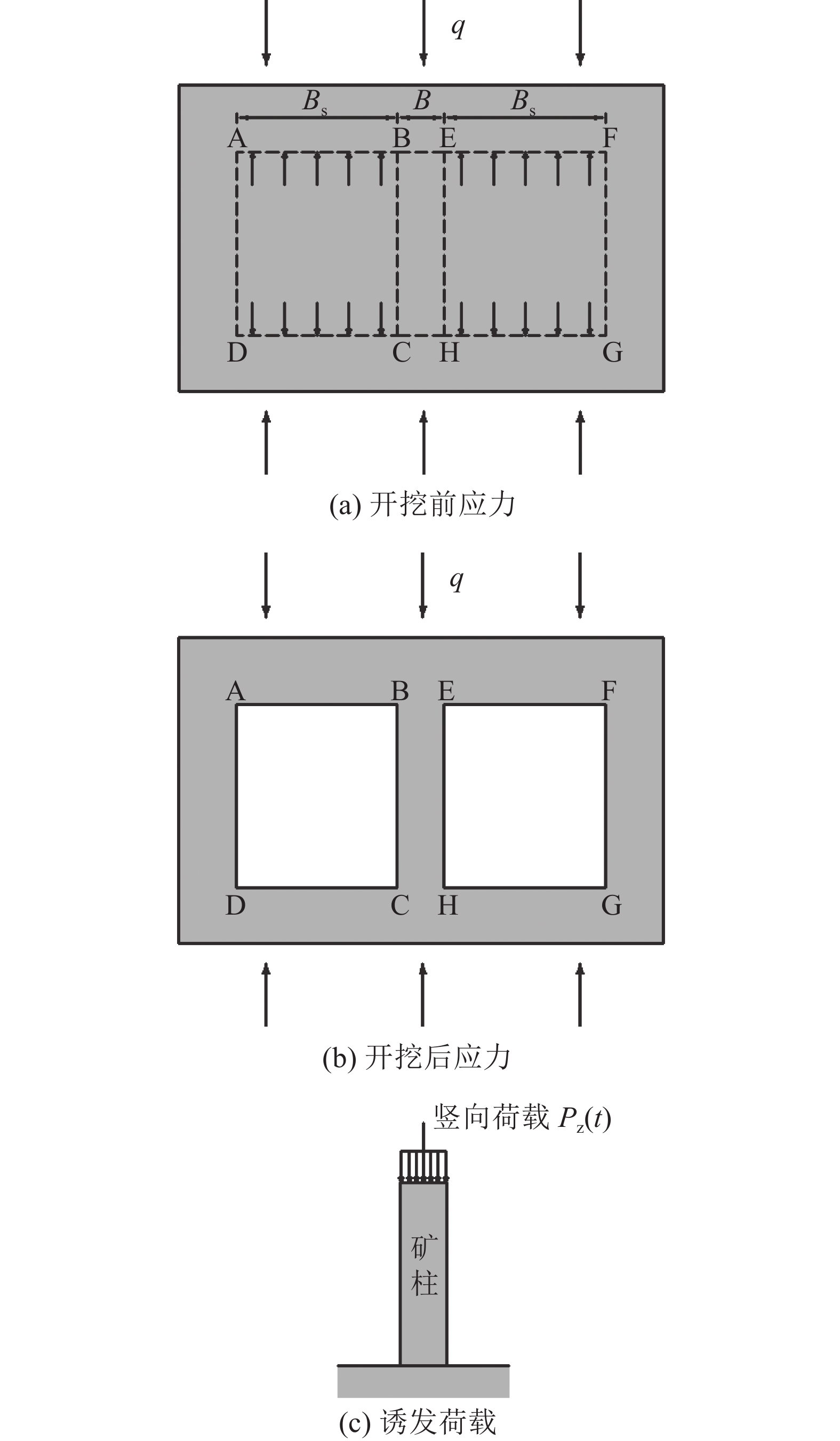
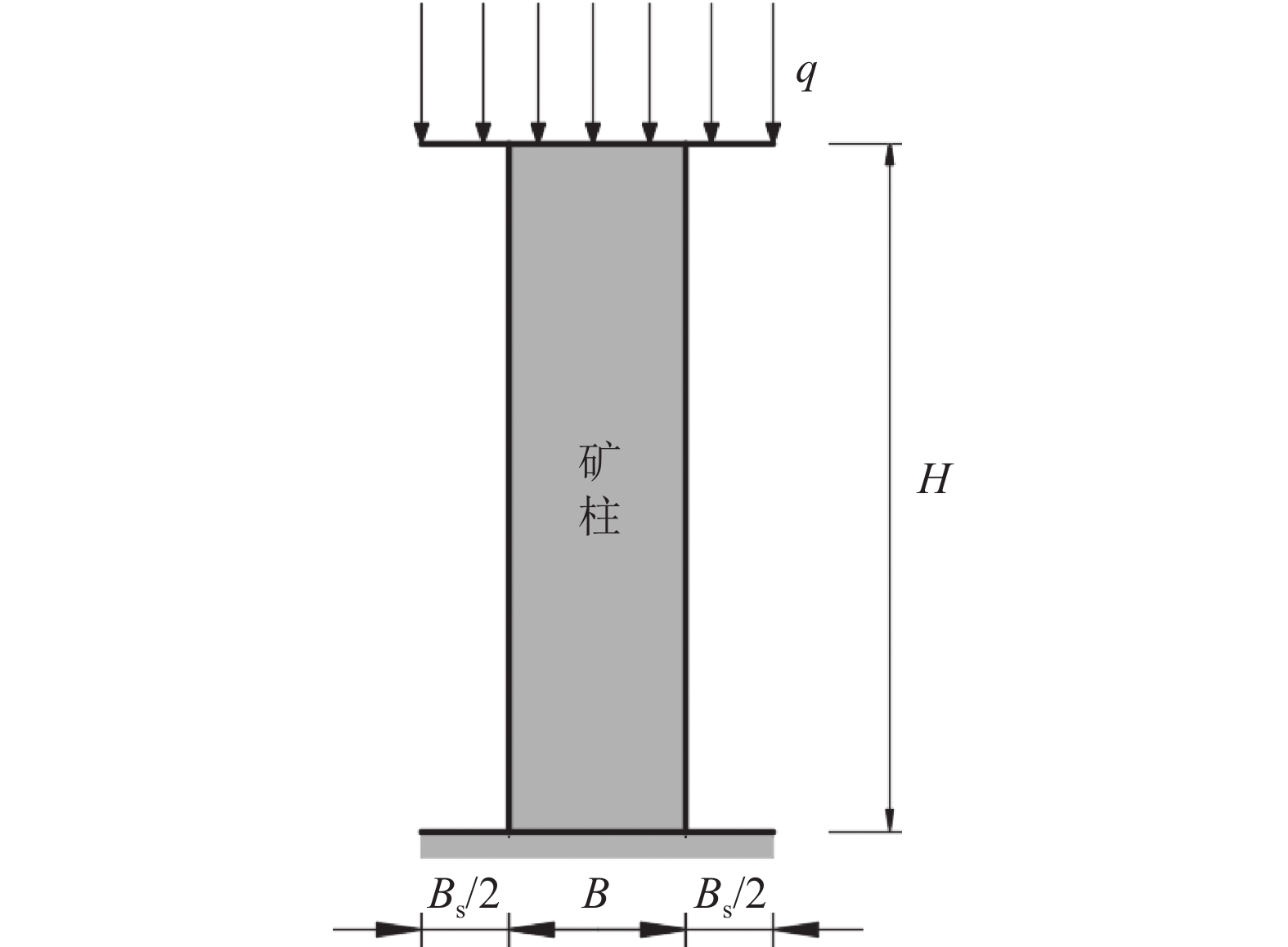
假设矿体沿走向布置长度足够大，且横截面积不沿长度方向变化，进而将此问题视为平面应变问题进行弹性力学理论求解。采用刚性基础上的具有预应力的岩石支柱代替矿柱响应，研究单位厚度的矿柱，其简化力学模型如图1所示。图1中，q为矿柱顶部所承担的荷载。

图  1  矿柱稳定计算简化力学模型

Fig.  1  Simplified mechanical model for pillar stability calculation

下载: 全尺寸图片

为使研究更加简便，作出弹性力学相关假设^[12]：矿体必须是均质、受力均匀、各向同性，同时满足连续性和完全弹性的条件，并且仅有轴向受力和变形。

1.2   矿柱承载理论

生产实践已经形成了计算矿柱顶部荷载的方法，包括面积承载法^[13]、压力拱法^[14]和Wilson理论法^[15]等。在深部开采领域，最为适用且认可度较高的是面积承载法，该方法认为矿柱所承受的载荷是其支撑顶板范围内上覆全部岩体的自重应力，偏高估计了矿柱顶部的荷载大小，设计使用时具有较高的安全裕度。以图1所示的矿柱简化力学模型为例，矿柱承受顶部及两侧相邻矿房各一半的上覆岩体自重，则矿柱的承载量P_f可表示为：

式中：B为预留矿柱宽度；B_s为开挖矿房宽度；q为岩体自重应力， $q{\text{ = }}\gamma {H_{\text{0}}}$ ，H₀为埋深，γ为岩体重度。

1.3   矿柱强度

矿柱强度受矿石强度和矿柱尺寸等多种因素的影响，国内外研究人员通过大量试验研究和工程实践总结出了几种计算矿柱强度的公式，比较有代表性的有Salamon强度公式^[16]、Bieniawski公式^[17]及由此发展推广出的一些经验公式等。从试验可知：采场的保留矿柱的宽高比（ $B/H$ ）对矿柱强度影响较大；矿柱形状对矿柱强度也有影响。考虑矿柱形状及尺寸影响，则矿柱强度可用式（2）^[18]表示：

式中： $ {\sigma _{\text{R}}} $ 为构成矿柱的矿石抗压强度；H为矿柱高度；α、β为常数，可通过试验确定，对于深埋金属矿山，常取α=0.5，β=–0.5。因此，矿柱强度计算公式可表示为：

1.4   确定矿柱尺寸参数

强度计算理论认为矿柱上的载荷达到其极限承载力即发生破坏，确定矿柱尺寸参数不仅要保证矿柱稳定，还应保证具有一定的安全裕度。取安全系数k为矿柱强度与矿柱平均应力的比值，表示为：

将式（1）和（3）代入式（4），可得矿柱稳定性的计算式：

将相关参数代入式（5），可得矿柱静态稳定下的矿柱尺寸参数。

2.   矿柱尺寸参数确定的能量法

2.1   快速开挖方式下矿柱能量转化特征

能量法因可以避免分析采场结构失稳破坏过程的复杂受力应变过程^[19]而得到广泛应用。因此，作者从能量角度出发，探讨开挖扰动作用下的矿柱动力响应和能量转化过程。

图2为某采场开挖前后的应力变化及矿柱受力状况。为简化问题研究，以一种单轴受压情况进行分析，假设采场仅处于自重应力场中，自重应力为q。

图  2  开采前后应力变化及矿柱受力状态

Fig.  2  Changes of stress state before and after mining and the stress state of the pillar

下载: 全尺寸图片

对于矿柱系统，考虑主应力，则矿柱系统总能量为^[12]：

式中，σ₁、σ₂、σ₃分别为岩体单元的最大、中间、最小主应力，ε₁、ε₂、ε₃分别代表最大、中间、最小主应变。

岩体内部储存的弹性应变能为：

式中，E为岩体弹性模量，ν为其泊松比。

如果仅考虑单向荷载作用，未开挖状态下矿柱 $\sigma_1=q$ ， $\sigma_2=\sigma_3=0$ ，代入式（7）可得矿柱的初始应变能为：

开挖后，先前由上覆岩体作用于围岩ABCD和EFGH面上的支撑荷载将平均地分配到中间预留矿柱和两侧支柱上。假定诱发荷载在整个矿柱面上均匀分布，以竖向荷载P_z(t)的形式随时间变化作用于矿柱顶部，如图2（c）所示。

根据面积承载理论，矿柱两侧矿体开挖后，矿柱顶部产生的最终承载力P_f为：

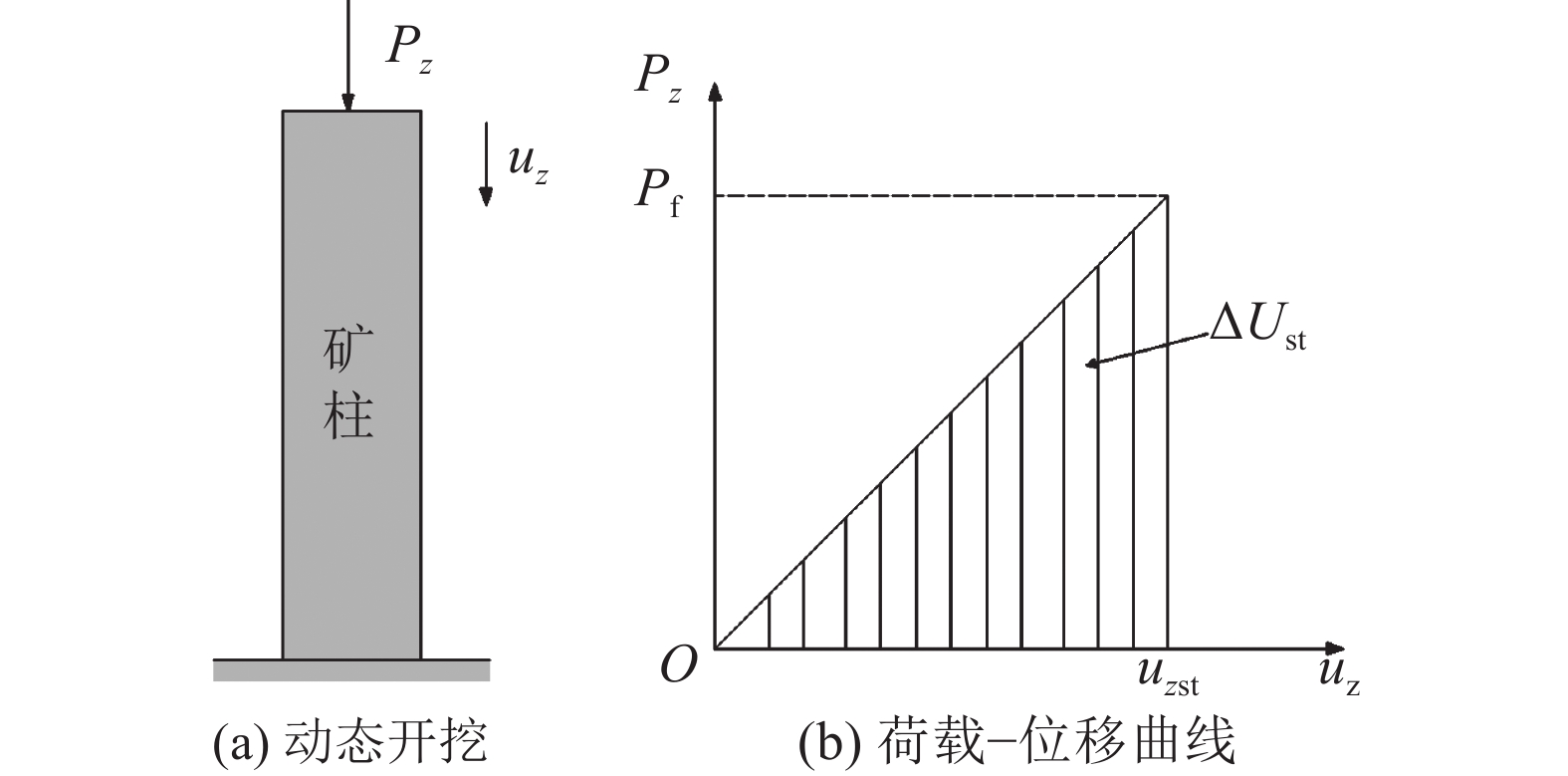
若不考虑动态开挖作用，矿柱受开挖影响诱发产生的应力 ${\sigma _{{\textit{z}}{\text{st}}}} = \dfrac{{{P_{\text{f}}}}}{B} = \dfrac{{{B_{\text{s}}}}}{B}q$ ，矿柱的最大主应力 ${\sigma _1} = q + {\sigma _{{\textit{z}}{\text{st}}}}$ ，由式（7）可知，此时矿柱的静态应变能累积量为：

进而，矿柱的静态应变能增加量可表示为：

图3为矿体动态开挖作用下矿柱顶部诱发荷载的时程曲线P_z(t)。从矿体回采开始，假定矿柱诱发荷载呈线性变化，直至矿体完全回采（u_z=u_zst时），诱发荷载趋于稳定，达到最大值P_f。

图  3  动态开挖过程中矿柱的诱发荷载–位移曲线

Fig.  3  Induced load-displacement curve of pillar during the dynamic excavation

下载: 全尺寸图片

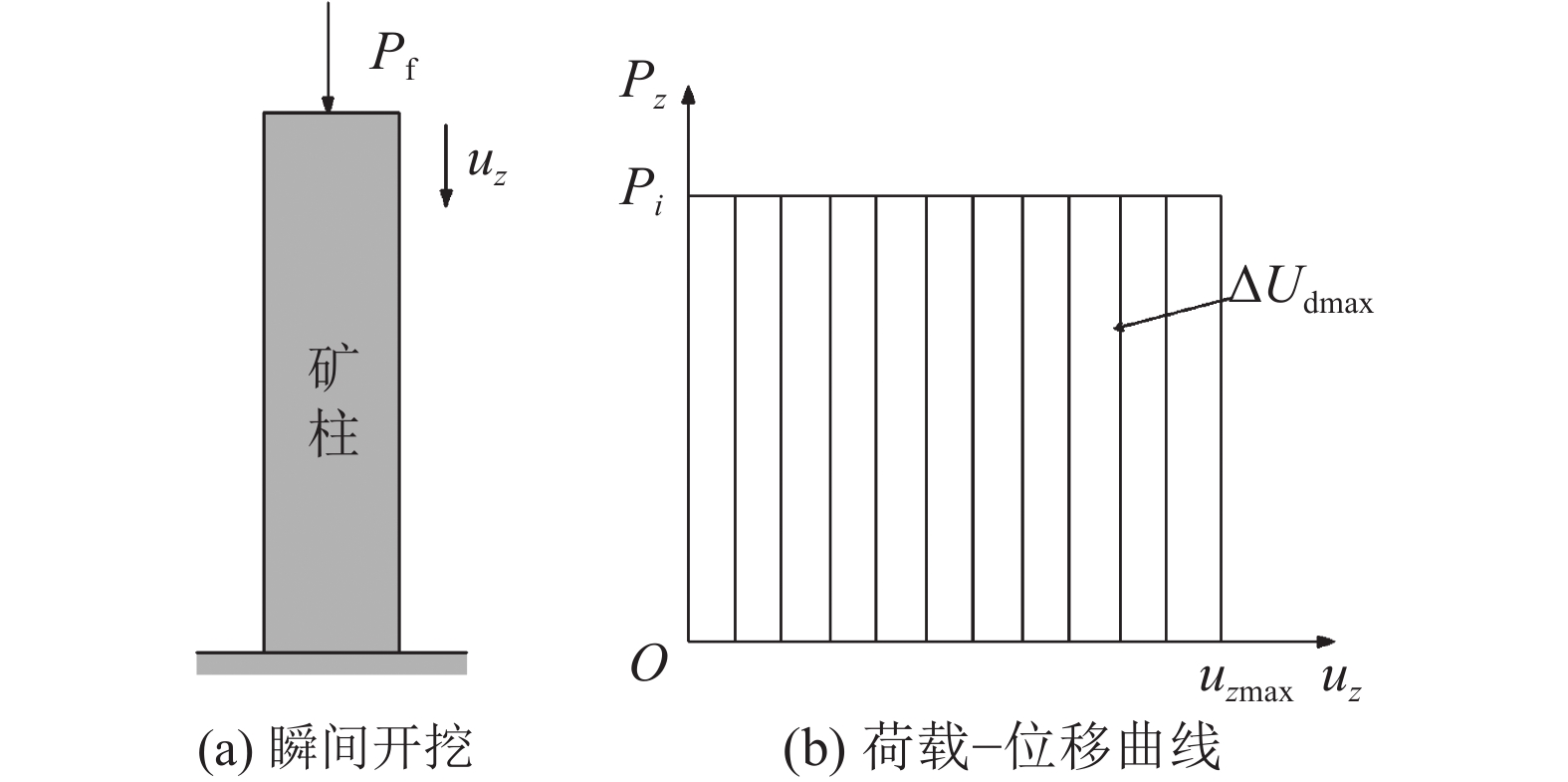
考虑极端情况，即矿体瞬间开挖后所有诱发荷载瞬时地作用于矿柱顶部，诱发荷载在矿柱轴向变形的全过程内均为恒定值，其大小为P_i；受瞬间加载作用，矿柱将产生一定的轴向压缩响应，如图4所示。

图  4  瞬间开挖后矿柱的诱发荷载–位移曲线

Fig.  4  Induced load-displacement curve of pillar after instantaneous excavation

下载: 全尺寸图片

此时，矿柱产生的动态最大轴向压缩量 ${u_{{\textit{z}}{\text{max}}}} = {\varepsilon _{{\textit{z}}{\text{max}}}}H = \dfrac{{{\sigma _{{\textit{z}}{\text{max}}}}}}{E}H$ 可表示为：

式中，ε_zmax、σ_zmax分别为瞬间开挖作用诱发的矿柱最大应变和应力值。

外荷载系统所做的功将全部转化为矿柱应变能的增加 $\Delta {U_{{\text{dmax}}}}$ ，其表达式为：

由式（8）和（13），可求得矿柱的应变能最大累积量为：

此时，矿柱的 ${\sigma _1}{\text{ = }}q{\text{ + }}{\sigma _{{\textit{z}}\max }}$ ，由式（7）可知，矿柱应变能的最大累积量还可表示为：

联立式（12）、（14）和（15），可求得：

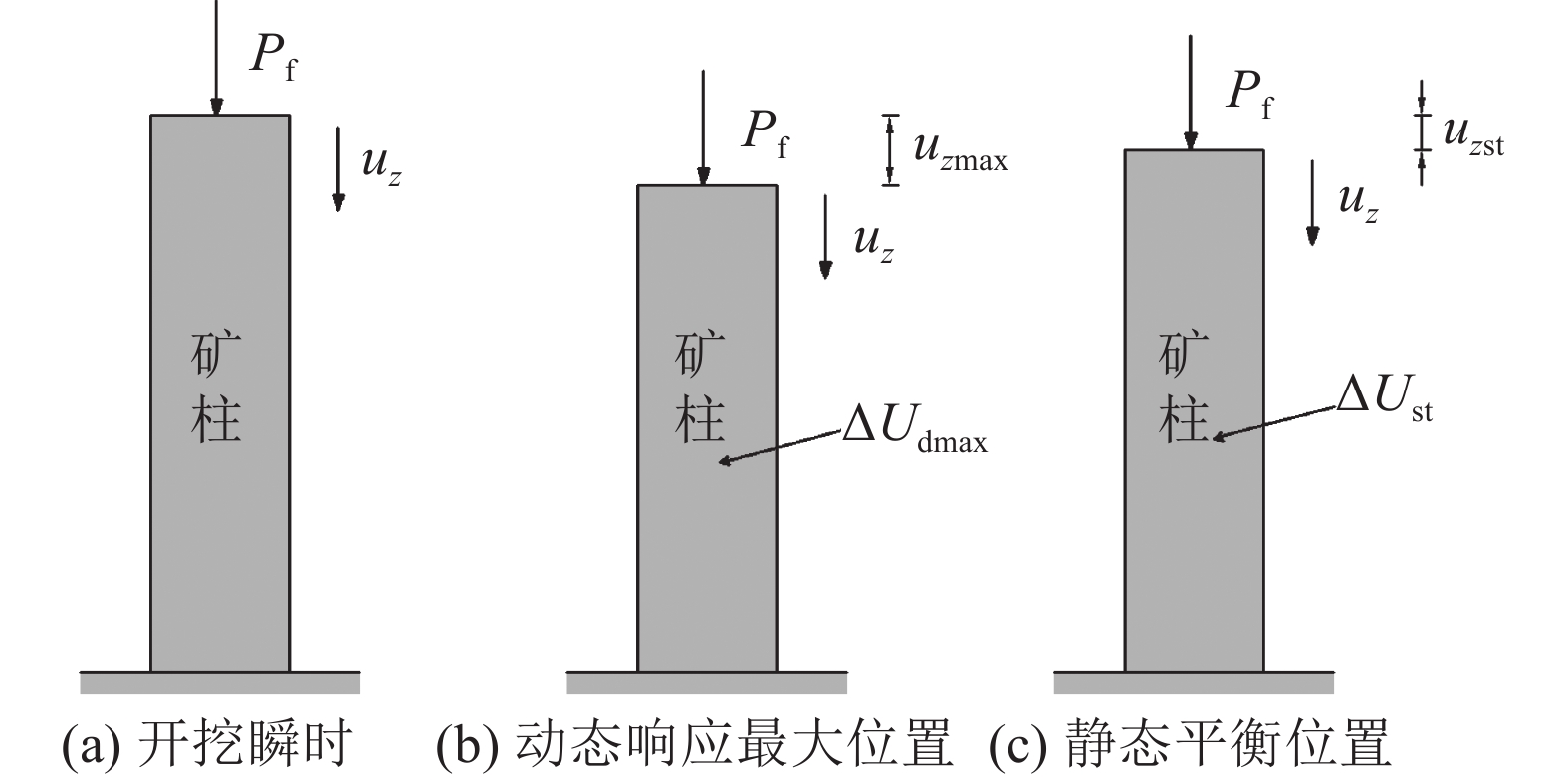
式中， $ {\sigma _{{\textit{z}}{\text{st}}}} $ 、 $ {u_{{\textit{z}}{\text{st}}}} $ 为静态平衡状态下的矿柱稳定应力和轴向压缩量。

综上可见，当考虑矿体的动态回采过程，特别是矿体瞬间回采完成的极端情况时，矿柱体产生了较大的动态响应，其动应力和动态变形可达静态时的两倍，矿柱尺寸参数设计不能忽视这一动态过程的影响。

之后，矿柱会由最大轴向压缩状态不断振荡回弹直至静态平衡状态，如图5所示。

图  5  瞬态开采后矿柱的振动回弹

Fig.  5  Vibration rebound of the pillar after transient mining

下载: 全尺寸图片

根据能量守恒定律，矿柱应变能的最大储存量 $ {U_{{\text{dmax}}}} $ 中的部分将以其他能量形式耗散到周围岩体中，表达如下：

式中：W为矿柱位置势能的增加量； $ {U_{{\text{st}}}} $ 为矿柱静态平衡时应变能的累积量； $ \Delta {U_{\text{v}}} $ 为矿柱中由于不断振动释放到围岩中消耗的能量，不考虑热量损失时，这一能量也是矿柱中转化为动能的部分。

瞬态开挖稳定后，矿柱由压缩变形最大值u_zmax变化至u_zst位置，这一过程矿柱受外力大小为（P_f+qB），故矿柱位置势能的增加量等于这一外荷载所做的功，即：

进一步结合式（10）、（18）和（19），得到矿柱对外释放的动能 $ \Delta {U_{\text{v}}} $ 为：

2.2   能量法

在金属矿山的实际生产中，为提高生效效率，采场高度一般设计较高，预留矿柱的高度较大，故矿柱的形成并非一次钻爆开挖作用，而是常采用分层爆破开挖的方式^[20]。假定矿体两侧爆破开挖分层数为n，且每层的开挖高度相等，均为ΔH，如图6所示，则有：

图  6  矿体分n层等高回采示意图

Fig.  6  Mining schematic diagram of orebody with n-layer and equal height

下载: 全尺寸图片

矿柱尺寸参数的设计应以最不利的情况进行。由第2.1节可知，在第n层开挖时，此前n–1层开采诱发动力响应已经振动回弹至平衡状态，矿柱整体能量积累最大值应出现在第n层诱发产生最大轴向压缩变形位置。对于矿体前n–1层的钻爆回采，每层回采动力稳定后的矿柱应变能增加量为：

对于第n层回采，矿柱应变能增加量应考虑钻爆开挖诱发的最大值，即：

结合式（22）和（23），得到矿体分n次等高钻爆开采后，矿柱最大应变能增加量为：

定义开挖分层系数组 ${f_n}(f_{\text{1}}^n,f_2^n)$ 表征矿体由于分阶段钻爆回采对矿柱系统能量转换的影响，其中 $ {f}_{1}^{n}=1+\dfrac{3}{n}，{f}_{2}^{n}=2+\dfrac{2}{n} $ ，则式（24）可变为：

此时，矿柱内部储存的应变能为：

从能量角度校核矿柱的稳定性，当岩体中可释放的应变能大于岩体内部储能极限时，岩体整体将发生动态失稳。利用谢和平等^[21]提出的基于可释放能量的岩体整体破坏准则，并代入式（3），则岩体内可以储存的最大应变能表示为：

式中，U_s为岩体单元储能极限。

矿柱不会发生动态失稳的条件为^[21]：

将式（26）和（27）代入式（28），并考虑一定安全裕度的要求，取安全系数为k，则确定矿柱尺寸参数的能量法表示为：

综上，只需要获得σ_R、B_s、q等相关参数，并根据钻爆分层数确定开采系数数组 $ {f_n}(f_1^n,f_2^n) $ ，依据式（29）可最终得到矿柱考虑动态开挖过程下的矿柱尺寸参数的临界值。

3.   工程实例

3.1   工程概况

某铁矿埋深均在650 m以下，最大埋深达到1 900 m，属深井开采矿山。根据其可行性研究报告的推荐，矿山设计拟采用房柱法。为保证一定的生产效率和经济效益，矿房开挖尺寸基本确定，约为80 m（长）×20 m（宽），并在垂直矿体走向的相邻矿块之间留设20 m间柱。

计划一期开采埋深1 020 m以上矿体，矿区内地应力可达20 MPa及以上，深部高地应力条件下矿体回采诱发的松弛变形、地应力卸荷破坏及冲击地压现象等都将使采场矿房矿柱结构稳定性及安全管理等方面面临巨大挑战，因此，合理选择矿柱尺寸参数是保证矿山安全生产的关键。

3.2   工程应用

采用能量校核矿柱动态稳定性，对该铁矿地下采场预留矿柱的尺寸进行设计并给出施工分层建议。根据其工程资料及相关技术报告可知，矿房宽度B_s为20 m，采场内铁矿石的天然密度为3 410 kg/m³，则埋深1 020 m水平采场的竖向地应力q=γH₀=34.1 MPa，室内试验测得矿石的抗压强度σ_R为160 MPa。

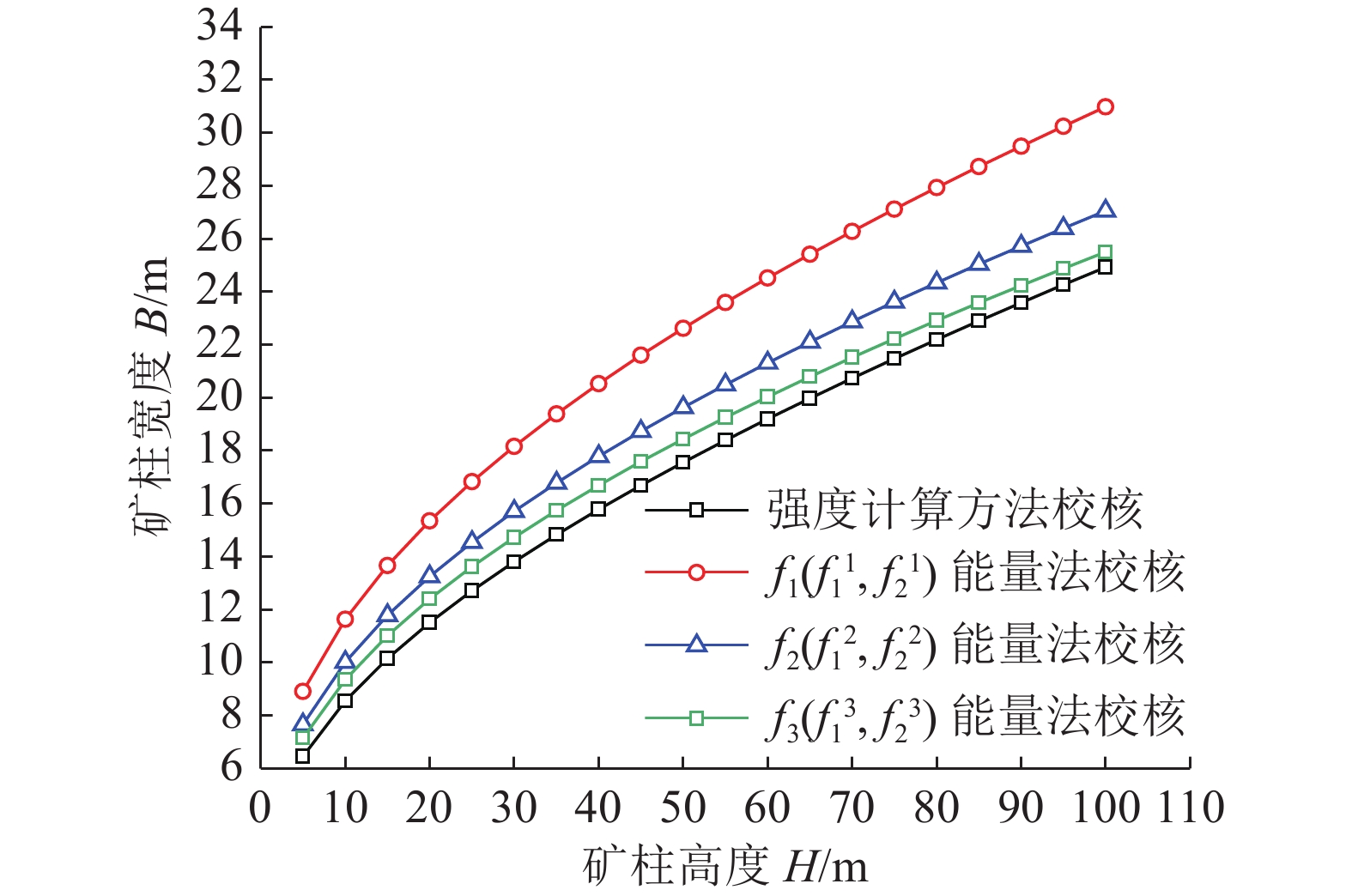
采用传统强度计算方法，矿山的安全系数k取1.5～2.0，可基本满足工程要求^[13]。考虑到本文提出的能量法已经充分考虑了动力扰动作用，可适当偏小，取该铁矿地下采场矿柱稳定的安全系数不低于1.3。应用第2.2节的能量法，并分别考虑矿体分1、2和3次钻爆开挖的情况，即取开挖系数为 $ {f_1}(f_1^1,f_2^1) $ 、 ${f_2}(f_1^2,f_2^2)$ 和 ${f_3}(f_1^3,f_2^3)$ ，得到保证矿柱系统回采过程中动态稳定条件下的矿柱临界尺寸，并与传统强度计算得到的结果对比，如图7所示。

图  7  能量法确定的矿柱尺寸参数临界值（k=1.3）

Fig.  7  Critical values of pillar size parameters determined by energy method (k=1.3)

下载: 全尺寸图片

由图7可知，在给定相同安全系数时，应用能量法相比传统强度计算方法得到的矿柱最小安全宽度更大，最大高度低，矿柱尺寸参数偏向保守。这也意味着使用传统强度方法设计得到的矿柱尺寸不能很好地满足动力稳定需求，其忽视了矿柱因动态回采过程而产生的剧烈动力响应，在满足静力稳定的同时却存在矿柱动力失稳的可能，因此，在进行矿柱尺寸参数设计时，应采用能量法。

由图7还可发现，随着开挖分层数n的逐渐增多，当分3次或更多次数对矿体进行回采时，能量法得到的矿柱尺寸参数逐渐趋近于静态计算的结果。根据第2.2节中的讨论，每次开挖后矿柱受瞬态开挖作用影响而储存的动态响应应变能都得到了一定程度的释放与缓解，当分层数n足够大时，矿柱能量的累积过程近似于准静态情况，此时能量法与强度计算理论是等价的，传统强度计算方法是一种特殊情况下的能量法。这也从侧面说明了能量法应用于矿柱尺寸参数设计的合理性。

结合图7，在尽可能地满足生产效益需求的基础上，建议矿柱宽度合理范围为20～24 m。由于中国目前金属矿山的一般开采中段为40～50 m，考虑到设计矿柱高度较大，在实际回采时应以3次（层）回采为宜，还可以有效缓解矿柱动态响应的影响。因此，提出5种设计方案，见表1。

3.3   数值模拟

为了更真实地还原矿柱体实际的状态，采用显式有限差分方法（FLAC3D）模拟矿体回采矿柱形成过程。通过运动方程进行求解，可以有效地追踪岩体内部应力应变的动态变化过程^[22]，模拟瞬间回采后地应力的调整过程，真实地反映矿柱受瞬间开挖作用后的动力响应。

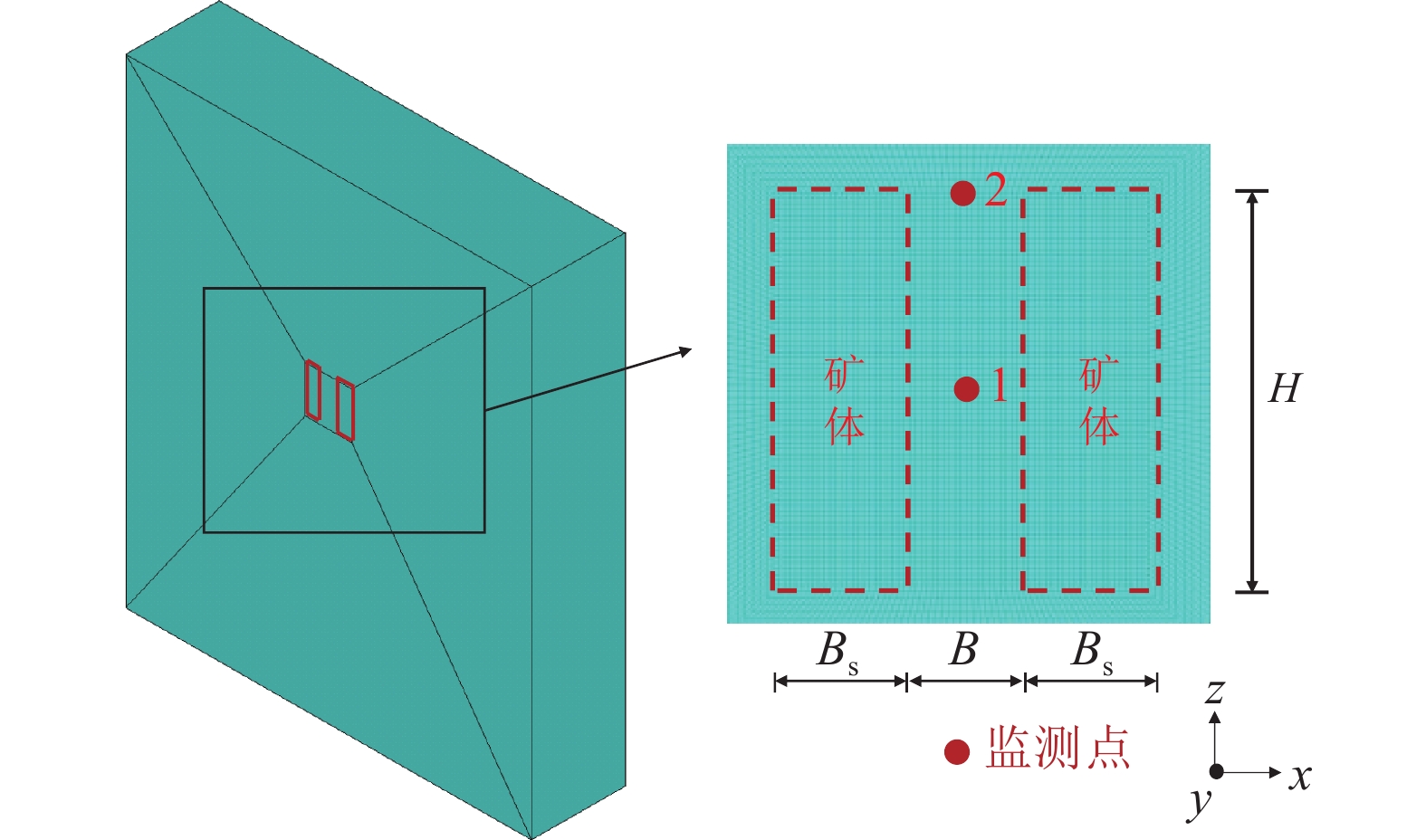
构建3维数值计算模型，并保证单元尺寸小于（1/10～1/8）波长，控制不同尺寸参数方案下矿柱单元尺寸均为1 m；同时，在矿柱左侧边墙中心位置设置振动速度监测点，如图8所示。图8中：模型底部采用全约束，侧面采用法向约束；原岩应力采用真实的3维应力场，经现场试验测得埋深1 020 m水平下竖向应力约21.00 MPa，水平最大主应力25.20 MPa，水平最小主应力22.32 MPa。对表1中的5种方案分别进行两侧3层等高回采模拟，通过先开挖最下面的一层，计算平衡稳定后再开挖上一层的方法实现。同时，利用内置FISH语言，撰写记录能量变化的FISH函数实现对能量累积过程的监控。

图  8  数值计算模型

Fig.  8  Numerical calculation model

下载: 全尺寸图片

由于矿柱的破坏形式以剪切破坏为主，故数值模拟中常采用Mohr–Coulomb屈服准则模拟岩体的屈服特性^[23]。数值模拟时假设模型内岩体种类单一，模型整体材料均用铁矿石模拟，经室内物理力学试验测试并经过折减换算，其材料参数取值见表2。

对表1中5种拟定方案进行数值优化，其矿柱的能量累积情况如图9所示。由图9可知：矿体回采完成后，受地应力重新分布的影响，矿柱的能量得到累积和调整，在矿柱中下部位置形成一定范围的应力集中区，聚集了较多的应变能。随着预留矿柱宽度的增大，矿柱内部应变能集中程度也越来越高，其中：以矿柱宽度20 m、高度60 m（方案1）对应的能量集中范围最大，且矿柱单元最大应变能也最大，约为24.50 kJ；矿柱宽度24 m、高度85 m（方案5）的能量集中范围最小，矿柱单元最大应变能也最小，约为22.35 kJ。

图  9  5种方案的矿柱能量累积分布

Fig.  9  Cumulative distribution of pillar energy under five schemes

下载: 全尺寸图片

统计整理了矿柱表面测点3个方向的振动速度随计算时间步的变化，分别截取振动速度峰值出现的部分如图10所示。由图10可知：回采过程中，不同矿柱尺寸参数的矿柱体产生了不同程度的动力响应，且x方向的质点振动最为剧烈，y方向的质点振动较为平缓，y向与x、z向的振动速度相比相差一个量级；方案4对应的x向振动最不明显，也即边墙向洞内收敛振动响应最小，振动速度峰值约为0.074 mm/s；方案5对应的边墙竖向振动响应最微弱，z向振动速度峰值约为0.012 mm/s。

图  10  矿柱表面测点3向振动速度随计算时间步变化曲线

Fig.  10  Variation curves of three-dimensional vibration velocity of measuring points on pillar surface with calculation time step

下载: 全尺寸图片

统计各方案矿柱单元的最大应变能及矿柱表面测点3向振动速度峰值，并计算其各自的回采率见表3。由表3可知：方案1和方案2产生的能量积聚和动力响应均较大，不宜采用；方案4的动力稳定性相对更好，方案3和方案5动力稳定性差距不大；进一步比较后3种方案下矿山生产的经济效益，方案3矿体回采率为47.62%，相比方案4和方案5的回采率46.51%和45.45%，减少了矿体的损失。因此，综合安全性和经济性两个方面，建议采场内预留矿柱的最优尺寸参数为方案3，即矿柱宽度为22 m、高度为70 m，与工程实际设计方案基本一致。

4.   结论与展望

本文从能量角度出发，针对深埋矿山开采中动力失稳现象展开了理论计算和数值模拟研究，并确定矿柱尺寸合理参数，主要结论如下：

1）矿体动态开采作用诱发矿柱内部产生剧烈的动力响应，特别是在瞬间回采的情况下，诱发产生的动应力和动态变形可达静力分析时的两倍，矿柱稳定性分析不能忽视动力扰动作用的影响。

2）构建了矿体阶段性分层回采计算模型，通过引入开采系数组 ${f_n}(f_1^n,f_2^n)$ ，给出适应不同开挖分层数的矿柱尺寸参数设计方法，相比于传统静力方法有效避免了动力破坏的可能，且在分层数足够多时与静力方法等价。

3）依托某铁矿工程的预留矿柱尺寸设计进行了能量法分析，结合数值模拟对能量法建议的5种方案进行优化分析，综合考虑安全性和经济性，建议某铁矿矿柱的合理宽度为22 m，高度为70 m。基本同工程设计保持一致。

能量法在认识矿柱的动态响应、考虑高地应力岩体的动态失稳可能性方面具有一定参考价值。但也应注意，该方法是在一定假设的基础上完成的，包含传统静态强度计算理论的一些基本假定；并且，为了便于说明矿体的动态形成过程，假定矿柱两侧矿体同时回采，这些与实际情况相比存在着一定的差异，因此，能量法的应用还有待于进一步深入研究。